基于相控阵激光超声的裂纹衍射增强试验研究

高 锋， 周 虹， 黄 超

(1. 上海工程技术大学 航空运输学院， 上海 201620; 2. 上海工程技术大学 城市轨道交通学院， 上海 201620)

超声波方法是无损检测中最广泛的检测方法之一，由于非接触性、宽频带高灵敏度等优势，激光超声已经成为超声检测领域的重要内容[1-3]。根据场景不同，发展了主要3种方法：脉冲反射法、脉冲穿透法和超声衍射时差法(time of flight diffraction，TOFD),前两种方法借助A扫图的幅值大小和时间对缺陷定位定量分析，同时，需要距离-幅值曲线或深度补偿曲线对幅值进行对比和补偿，但结果的精度仍有不小的误差；TOFD技术相比其他两种方法，不但能对缺陷精确定量定位，而且具有较高的检测效率，单人便可完成TOFD最常用的D扫方法。为了进一步提高TOFD的定位精度和检测灵敏度，国内外学者进行了大量研究。迟大钊等[4]提出合成孔径聚焦(synthetic aperture focusing technique，SAFT)数学模型与TOFD法B扫图图像增强的处理方法，并加运算窗处理，埋藏深度缺陷深度误差不超过0.2 mm，角度误差不超过5°；Noroy等[5]通过16个延时光脉冲实现的相控阵激光源，结果表明纵波幅值提高了24 dB，信噪比也有了显著提高；Pei等[6]通过光纤激光器内部时间延迟完成激光相控阵，并结合TOFD检测方法和电磁超声换能器完成了信号的A扫图和B扫图，结果表明测量误差在较小的范围内；Han等[7]提出使用Barker码激励的双接收器改进的超声飞行时间衍射方法，衍射信号由匹配滤波器压缩获取来定量估计缺陷，长度误差不超过0.83 mm，角度误差不超过4.31°。Cooney等[8-9]利用扫描激光线源和点源对航空航天材料中的裂纹进行了评估和疲劳检测，结果表明，表面裂纹特征的成像能力明显增强。

然而，结合激光超声与TOFD技术研究成果较少，且以上研究主要是从信号处理方面来提高信噪比和分辨率，同时，在检测板件和表面裂纹时，激光TOFD方法通常需要激光源达到烧蚀阈值来提高信号的幅值，以此满足检测精度要求。因此，激光TOFD方法的进一步研究更加具有实际应用价值。

本文利用光纤皮秒激光器和高速旋转镜完成相控阵激励源，通过有限元方法建立二维瞬态激光超声力-固耦合模型，研究了不同裂纹尖端奇异点、相控阵激光源的不同位置和不同中心频率声波对衍射信号的影响，结合超声场的衍射理论和相控阵激光超声方法计算出信噪比和幅值对衍射信号的变化规律并进行分析，进行了试验验证和定量分析，探索在复杂环境下相控阵激光超声在TOFD技术中应用的最佳方法。

1 基本原理

1.1 衍射几何理论

考虑极短激光脉冲激发出极短的超声脉冲，根据频域上的统一衍射理论，发出的超声脉冲为点状声源，并且接收端位于源声场的阴影中，不考虑场变量的时间相关性，通过对二维空间圆柱坐标系下常见的直角尖端缺陷理论分析，如图1所示。声源S的位置为(rs,θs)，接收端R的位置为(rR,θR)，缺陷几何角度为nπ。从声源S出发，假设入射场为

图1 超声在尖端缺陷的衍射图

ui=A(rs)e-ikr′(s)

(1)

式中：kr′(s)为沿着该射线的相位；k为波数；A(rs)为rs的倒数。

在接收端R上的衍射声场[10]可表示为

ud=ui(Q)A(rs,rR)Dhe-ikr′

(2)

式中：Dh为衍射系数；Q为缺陷尖端衍射点；下标h为缺陷边界类型；A(rs,rR)为比例系数。根据三维空间声波方程理论，A(rs,rR)和Dh表达式分别为

(3)

(4)

其中距离参数

(5)

F(X)为菲涅耳积分的过渡函数形式，表示为

(6)

缺陷边界角度突变函数a±为

(7)

式中：ξ为入射光线与衍射点处边缘的法线的夹角；N±为满足等式2nπN±-α=±π的整数最小数值；α为声场与缺陷反射边界或者绕射边界上的突变角，将式(1)～式(7)联立便可得出二维空间超声衍射场分布情况。

1.2 相控阵激光超声的裂纹尖端衍射增强理论

等间距排列的激光脉冲经过时间调制后，检测声束同时到达检测点处。对于N个激发源激发出的位移叠加后表示[11]为

(8)

式中：下标t为时间；Rm为球形传播因子，对于三维空间中传播的横波与纵波，m取1；θ为单个激发源激发的超声波方向角；D为激发源与声波模式相关的方向性函数；B为阵列因子(关于激光脉冲的时间间隔Δt、激发源到检测点距离r和声波速度c的函数)；I为反映激光脉冲源特征的激发函数。考虑连续波束偏转法则的远场特性，波束方向性函数D的表达式可表示为

(9)

式中：Dp(ψ,θ)为远场区域一点源方向性；ψ为点源与激励源中心的角度；R为点源与激励源中心的距离，其表达式推导为

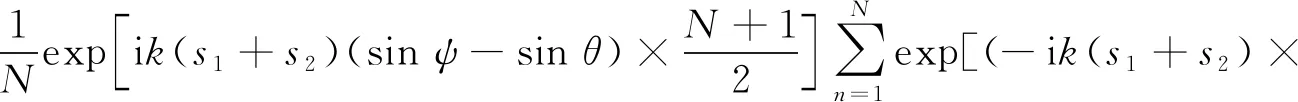
(sinψ-sinθ)n]

(10)

式中：s1为激光线源长度；s2为每个激光激励源的间隙；对上述序列求和可得

(11)

2 数值计算研究

2.1 有限元模型

本文采用有限元软件COMSOL对瞬态超声进行数值计算[12]，在计算工程中，用等效力源代替激光源，利用固体力学物理场模拟激光束入射在铝块表面上引起局部热膨胀并激发出超声波，同时不考虑Y方向的应变和波场位移,可以将模型简化为X-Z二维平面来研究[13],为了减少边界处的反射干扰，将左侧和右侧设为低反射边界[14]，底边设置固定约束，模型如图2所示。其中：xd为表面缺陷的深度；xw为缺陷宽度；所用试验材料是铝，属性参数如表1所示。相控阵激光源每根激光束等效力源线宽s1=2 mm，间隙s2=1 mm，峰值功率密度控制在5×106W·cm2以下，不超过铝的损伤阈值，相控阵激光源通过3个等效力源时间调制[15-17]，每个激励源时间延迟设置为0.2 μs。

表1 有限元模型中铝的材料参数

(a) 同侧缺陷

2.2 有限元计算结果分析

2.2.1 不同激光源的影响

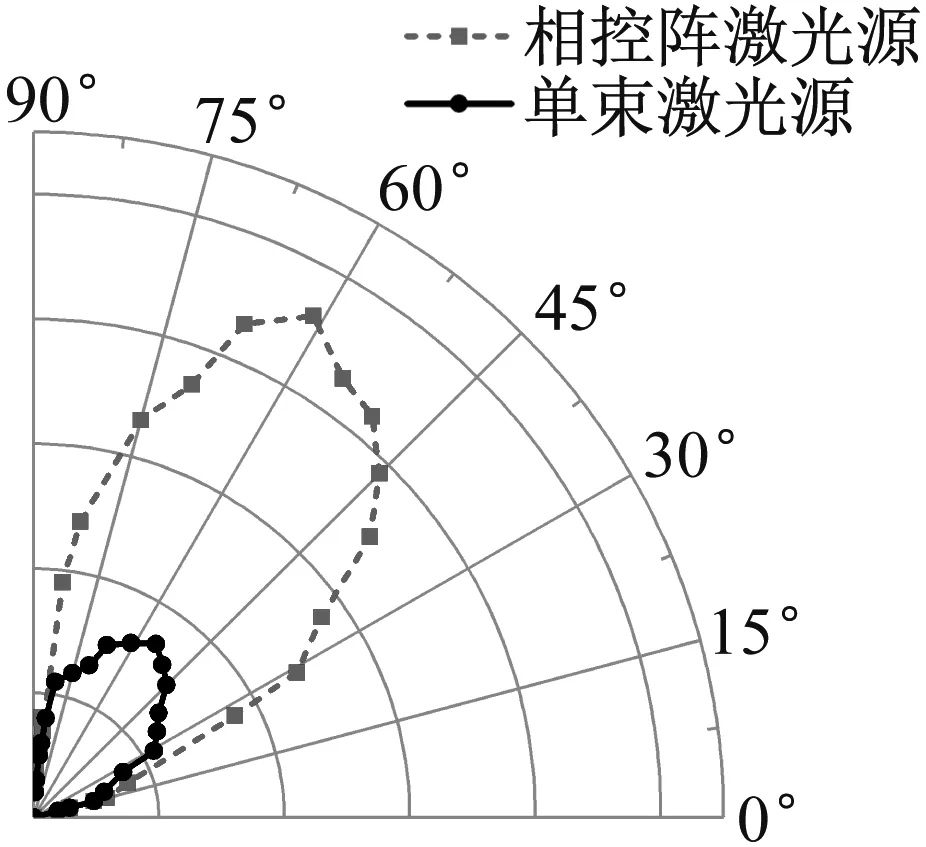
热弹机制下单束激光源与相控阵激光源的纵波与横波的方向性图，如图3所示。极坐标原点到节点的距离为声波幅值，可以看出，声波的方向性是关于表面的法线对称[20]的，纵波在法线两侧以单瓣形式向外辐射，在60°角左右时幅值最大，而横波在法线两侧按照双瓣形式向外辐射，主瓣约在30°角时最大；经过三束相控阵激光源作用后，根据式(8)的计算，可以看出纵波和横波最大幅值处约增强了两倍，并且与单束激光源产生的横波和纵波方向差距较小，说明本文设置的参数使得相控阵激光源产生的纵波和横波偏转角度达到了几乎最优的效果。

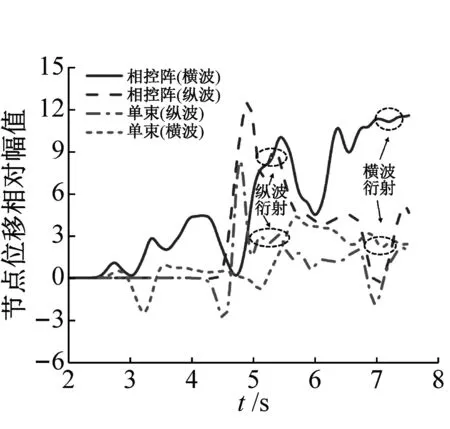
根据横波和纵波的传播方向和速度的差异，图4显示了内部缺陷和表面缺陷典型的两种检测方式，设置参数xd=7 mm，xw=0.3 mm，fc=2 MHz，从图4(c)、图4(d)可以明显观察到通过相控阵激光源，朝向裂纹的纵波(P)幅值明显增强，且从图4(d)中可以看出更强的衍射波，尖端横向衍射(PTS纵波转换横波)和尖端纵向衍射(PTP纵波转换纵波)，与图3的方向性规律一致；从图4(b)、图4(d)对比看出纵波(P)在异侧缺陷尖端处的衍射信号传播路径更加明显，而对于同侧缺陷图4(a)和图4(b)，横波的衍射信号则不易看出，与图5(a)显示的相对位移幅值有较好的一致性。图4中STP为横波转换纵波；S为横波。根据式(8)计算，图5(b)显示了附近节点处的S波和P波衍射场的相对位移振幅，在P波衍射场的节点(27，7)处可见明显的衍射信号，相比横波，由于S波速度较低，STS(横波转换横波)信号很容易被来自试样背面或缺陷表面的反射或模式转换信号淹没，因而在S波衍射场的节点(27, 23)和(27, 21)处存在较小的衍射横波，同时，热弹效应下的横波垂直于材料表面形成非常小的入射角，需要尺寸较小、高灵敏度的电磁声换能器[21]在距离声源较小的距离才能有效的接收。如图5(c)所示，相控阵激光源中纵波在尖端衍射处信噪比约增强为两倍，横波衍射处信噪比约增强为1.5倍，但总体上纵波衍射信号信噪比远大于横波衍射信号信噪比，因此后续影响因素的研究均在纵波传播下进行计算。

(a) 纵波

(a) 单束激光源横波

(a) 不同激光源相同节点位移

2.2.2 缺陷尖端奇异点的影响

在相控阵激光源下的尖端不同数目奇异点的衍射声场位移图，如图6所示。xd=7 mm，xw=0.3 mm，fc=2 MHz，根据不同数目奇异点分为不同种类尖端缺陷，图6(a)～图6(d)分别为V形尖端、三角形尖端、矩形尖端和圆弧形尖端的超声衍射信号云图，同理，选择附近节点(27, 7)和(27, 9)的位移幅值来研究不同奇异点缺陷尖端对衍射信号的影响。

如图6(a)和图6(b)所示，随着缺陷尖端奇异点数目增加，纵波(P)在尖端处的衍射信号幅值不断增加，矩形和圆弧形为两个奇异点，在不同节点处的衍射位移幅值相对一致，图中虚线框区域可以明显看出在三角形尖端衍射幅值最大；同时，对比图7(a)和图7(b)，在不同节点处衍射信号的幅值不同，缺陷尖端右侧约3 mm几点处衍射幅值在5.4 μs时幅值最高，而缺陷尖端右上侧节点在5.1 μs时幅值较小，但均与图6奇异点与衍射幅值的规律一致，在两个图衍射波峰后均出现了一波峰，并无明显的衍射规律；图7(c)显示了不同尖端奇异点衍射信号的幅值比，图7(c)中可见，随着缺陷尖端奇异点的增加，衍射信号信噪比也不断提高，这是由于衍射信号幅值的增加，同时各尖端缺陷的噪声信号并无明显差异，因此幅值比随着衍射幅值的增加而增加。

图6 不同尖端衍射声场位移云图

(a) 不同尖端在节点(27,9)处位移

2.2.3 激光源不同位置的影响

不同位置激光源的声场位移云图，如图8所示。其中：xd=7 mm，xw=0.3 mm，fc=2 MHz，图8(a)～图8(f)为相控阵激光源中间激光束线宽中心与缺陷尖端的不同水平距离，由图8可以看出，随着激光源与缺陷尖端的距离越大，衍射信号传播路径越不清晰，且在8 mm处传播路径较为明显，同理选择附近节点(27, 7)和(27, 9)。

如图9(a)、图9(b)所示，缺陷尖端附近节点(27, 7)和(27, 9)处位移幅值随着激光源与缺陷尖端水平距离不断增加时，位移相对幅值也有了明显的降低，同时，虚线框中可以看出在节点(27, 7)处位移幅值降低趋势呈近似线性关系，而节点(27, 9)处呈非线性关系。并且，从虚线框中看出，距离为6 mm和8 mm之间的衍射位移幅值差距最大，远大于其他间隔2 mm的位移幅值。图9(c)显示了激光源与缺陷尖端水平不同距离的衍射信号最大幅值比，即信噪比，可以看出距离为8 cm处信噪比最高，与图8得出的规律一致，随着距离的不断增大，信噪比呈现先增大后减小的趋势。

图8 相控阵激光源不同位置的声场位移云图

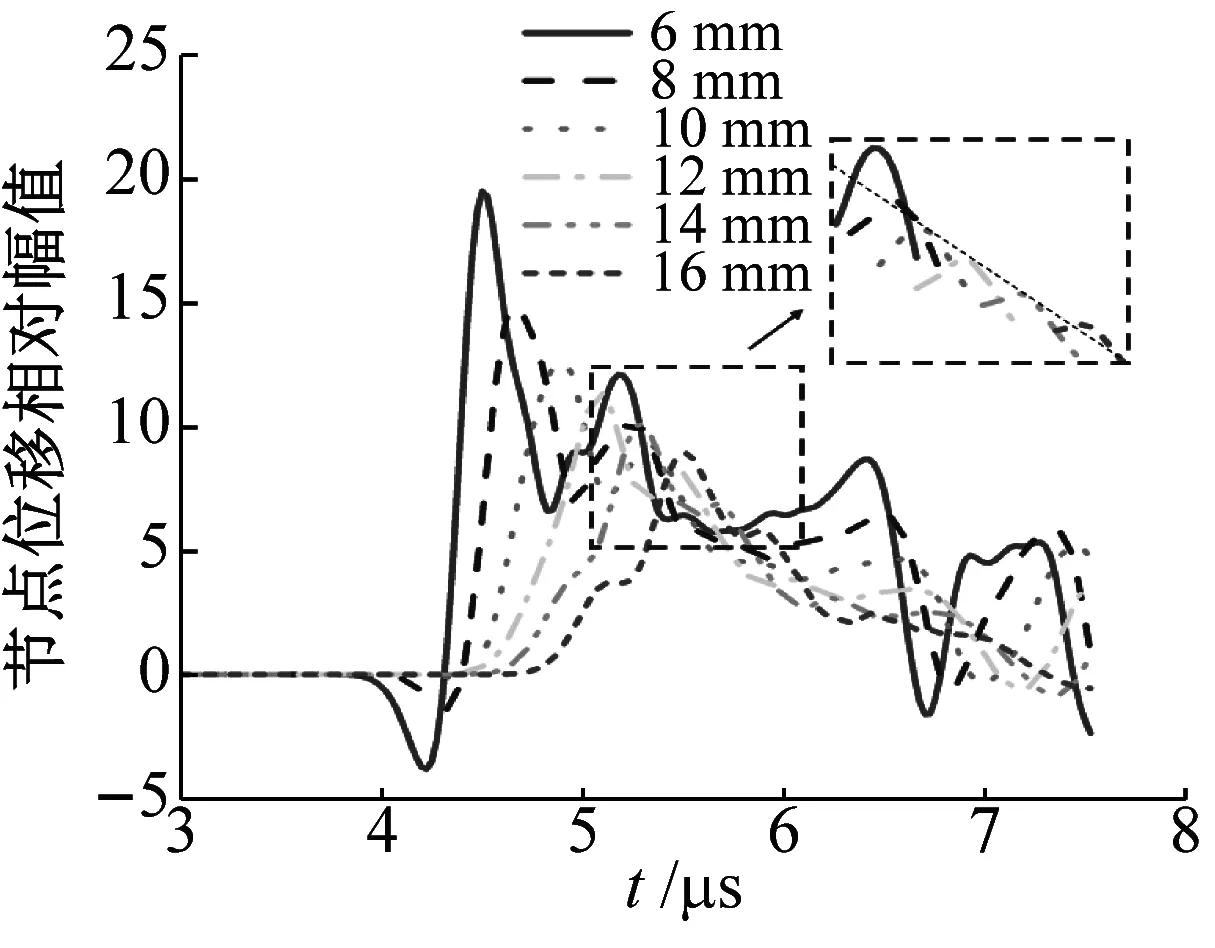
(a) 节点(27, 7)处位移幅值

2.2.4 声波不同中心频率的影响

如图10所示，可以看出激光等效力源是宽频带激发源，与脉冲激光源的宽带特性吻合很好，且中心频率越高的等效力源频谱范围越宽，可以激发更高频率的超声波，如图11为不同中心频率的声波对衍射信号幅值和信噪比影响图，由于纵波频率越大，衰减越快，因此选取1.0 MHz、1.5 MHz和3.0 MHz中心频率做对比试验，图11(a)可以看出频率越小，衍射信号幅值越大，且中心频率为3.0 MHz时出现了两个衍射信号波峰；图11(b)可以看出信噪比波动并没有明显的规律，由于频率小的信号在缺陷处易发生透射，频率大的信号在缺陷处易发生反射，因此在缺陷的左右两旁的衍射信号均受到透射波和反射波的干扰，而且，对比的中心频率差距不是很大，反射和透射现象比较一致，导致信噪比差距很小。

图10 不同中心频率的激光等效力源频谱图

(a) 节点(27,7)处位移幅值

3 试验验证

为了验证本文有限元数值计算的正确性，进行了试验验证。脉冲激光器选用德国IPG光纤高频激光发生器，波长为1 064 nm，聚焦光斑半径为1 mm，脉冲宽度为1 ns，单个脉冲最大能量为0.2 mJ，其他参数与有限元参数设置保持一致，接收端为中心频率为1.0 MHz和2.5 MHz的纵波斜探头，检测原理如图12所示。

图12 相控阵激光超声检测原理示意图

根据本文的有限元计算结果，由于纵波比横波对于裂纹缺陷检测信号信噪比更高，利用纵波衍射原理进行试验，如图13显示了转换纵波的信号传播模式，图13中：LTL1为纵波首次在裂纹尖端的衍射信号；L为纵波信号；LL为反射纵波(PP)信号；LTL2为纵波在裂纹基底的纵波反射信号沿着裂纹左壁到尖端后的衍射纵波信号；y1为相控阵激光源中心到纵波斜探头的距离；y2为裂纹尖端到激光入射界面的距离。同时，根据图中三角函数关系和纵波传播时间可以得出裂纹深度。

图13 纵波传播模式部分示意图

图14为单个激光源与相控阵激光源的裂纹A扫描信号图，样件尺寸(长×宽×厚)为200 mm×80 mm×30 mm的铝块，缺陷宽度为0.3 mm，长度为7 mm的底面裂纹，探头频率为1 MHz。图14(a)、图14(b)对比看出相控阵源激光束比单个激光束的裂纹尖端衍射信号幅度明显增加，且图14中LTL1和LTL2衍射信号延迟的时间缩短，信噪比更高；根据图14(b)和图14(c)对比得出三角形尖端衍射信号幅值大于V形尖端，且延迟时间更短，对比图14(c)和图14(d)得出激光源距离y1=8 mm衍射信号幅值明显大于y1=10 mm，且y1=8 mm衍射信号延迟时间缩短，信噪比更高。同时对比了探头频率为2.5 MHz的A扫描信号图，发现衍射信号幅值有小幅度减小且延迟时间无明显变化，表2和表3为多次试验求出的平均结果。如表2所示，分别对不同尖端奇异点、不同激光源距离和不同中心频率超声影响下的的延时信号LTL1位移幅值、信噪比和延迟时间试验数据进行了对比分析，从表2得出在三角形尖端下激光源处8 mm时信噪比最高，且延迟时间最短，在三角形尖端下激光源处6 mm时幅值最大，同时，在2.5 MHz中心频率下，衍射信号幅值略小于1.0 MHz中心频率，但信噪比和信号延迟时间均无明显变化。表3显示了相控阵激光源检测裂纹的误差分析，从表3看出，实际裂纹尺寸和检测裂纹尺寸误差均不超过6.8%，同时激光源8 mm处误差范围较小为2.5%～4.8%，而10 mm处误差范围较小为2.9%～6.8%。

(a) 激光源距离10 cm，V形裂纹尖端

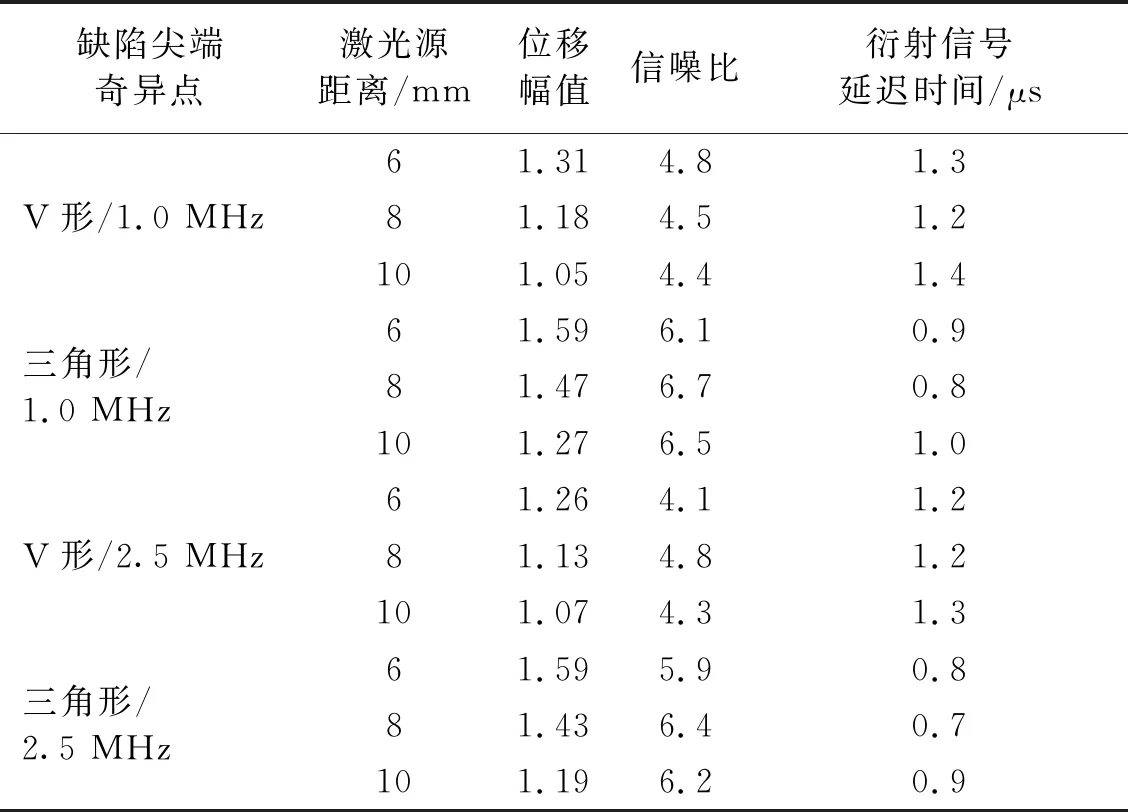
表2 相控阵激光源试验数据对比

表3 相控阵激光超声TOFD的定量检测结果及误差

4 结 论

本文考虑TOFD方法衍射信号幅值小、信噪比低等问题，通过皮秒光纤激光发生器和高速旋转镜来实现相控阵技术与激光超声检测的结合，代替传统单束激光源实现的TOFD检测方法，并通过有限元方法研究了不同距离激光源、尖端不同奇异点和声波不同中心频率对衍射信号的影响，并进行了试验验证，得到以下结论。

(1) 相控阵激光源对比单束激光源，衍射信号的信噪比和位移幅值有了明显的提高，且纵波比横波遇尖端衍射信号传播路径更加明显，信噪比更高。

(2) 裂纹尖端衍射信号幅值随裂纹尖端奇异点增加而增大，随声波中心频率减小而增大；衍射信号信噪比随裂纹尖端奇异点的增加而增大，随激光源与尖端水平距离的增大呈现先增大后减小的趋势，随声波的不同中心频率无明显变化。

(3) 定量计算裂纹长度时，同时考虑3种影响因素，不同中心频率的声波的影响较小，激光源距离裂纹尖端水平距离较小时与实际裂纹长度误差范围较小，距离较大时误差范围较大，同时，根据裂纹尖端不同奇异点对衍射信号的影响规律可以反演出尖端的大致类型。