基于核磁共振测井的储层渗透率计算方法综述

陈 瑶，何宗斌，覃莹瑶，童 新，陆 迪

(1.长江大学 地球物理与石油资源学院，湖北 武汉 430100；2.长江大学 油气资源与勘探技术教育部重点实验室，湖北 武汉 430100； 3.中国海洋石油国际有限公司，北京 100027)

渗透率是油气储层物理性质的基础，表征了地层允许流体流动和产出的能力，是衡量储层流体特征的参数之一，在油气田的不断深入开发中显得尤为重要。目前已知的测井方法中，核磁共振测井通过对氢核核磁共振测量结果的观测，可对地层孔隙中的流体及其含量进行识别[1]，同时反映了充满流体的孔隙尺寸，是与渗透率直接相关的测井方法。

自20世纪50年代中期核磁测井概念被首次提出以来[2]，核磁共振测井技术以其无损、快速、测量结果准确等优点，被广泛地应用于储层评价中。该技术是通过研究储层流体中的氢核在外部施加的磁场中所表现出的特性来描述储层的岩石物理特性和孔隙流体特性的一种测井技术。较其他常规的测井技术，核磁共振测井技术能够得到丰富的地层信息，可有效应用于复杂岩性、特殊岩性的储层，且能够得到较为有效的储层渗透率。在储集层测井评价中利用核磁共振测井技术，克服了常规测井技术易受井眼、岩性、地层矿化度影响等缺陷，为储层评价提供了新的方法与道路。

核磁共振测井可直接将测量信号与地层信息联系起来，地层孔隙中流体的T2可直接与孔隙大小一一对应，短T2组分对应小孔隙，长T2组分对应大孔隙，当孔隙中仅存在单相流体时，孔径大小可被刻度出来，进一步确定可动流体与束缚流体的体积，进而确定地层的渗透率，该技术在不同地层都有很好的应用[3-5]。

常用的渗透率计算公式多是基于Kozeny-Carmen[6-7]公式建立起来的。该公式主要参数为有效孔隙度、迂曲度和比表面积，将多孔介质等价于孔隙大小相同的迂曲毛管束，再结合达西方程求出渗透率：

(1)

式中，K为渗透率；φeff为有效孔隙度；τ为迂曲度；r为毛管半径。

Kozeny-Carmen公式是一个理论公式，认为渗透率主要与孔隙迂曲度和孔隙几何形状有关[8]。公式很好地表征了渗透率的影响因素，然而该公式具有很强的经验性，在实际的计算过程中易造成较大的误差。

核磁共振测井技术可以提供丰富的地层信息，核磁渗透率相较于常规测井方法求得的渗透率更为准确。然而，当前运用核磁共振测井计算渗透率的方法多种多样，本文根据不同的计算参数，将核磁渗透率计算方法分为了基于几何平均值的渗透率计算方法、基于截止值的渗透率计算方法以及复合方法共3类，对核磁共振渗透率计算方法进行了综述，为核磁共振渗透率的准确获取提供了思路。

1 基于几何平均值的渗透率计算方法

SDR模型[9]利用T2分布的几何平均值来估算渗透率，是较为经典的核磁渗透率计算模型之一。该模型通常对水层有较好的预测结果，但对于油水层，该模型的计算结果误差较大，主要适用于中高孔渗的储层，随着现在储层的复杂化，单一的SDR模型已无法满足生产实际的要求，许多学者对SDR模型中的系数[10-11]进行了修正，使该模型能够更好地在实际中进行应用。也有学者基于Kozeny-Carmen公式，提出将表面弛豫率引入SDR模型中可更好地进行渗透率计算[12-15]。

K=C(φ)m(T2gm)n

(2)

式中，C、m、n为常数；φ为孔隙度；T2gm为T2几何平均值。

周尚文等[16]发现了页岩核磁渗透率与几何平均值具有较好的正相关性，建立了T2gm单参数模型。此方法仅对该特定区域的页岩储层渗透率适用，对其他地区不同岩性储层的效果如何还不明确。

K=8×10-8exp(8.173 4T2gm)

(3)

姚艳斌等[17]提出了基于饱和流体和束缚流体的双T2几何平均值渗透率计算模型，该方法在页岩渗透率预测方面有着较好的适用性，考虑到了储层的复杂程度，可将其用于其他的低孔渗储层渗透率计算。

K=aT2gab(T2gb)c

(4)

式中，a、b、c为常数；T2ga为饱和水状态下的T2几何平均值；T2gb为束缚水状态下的T2几何平均值。

Chi等[18]将定向孔连通系数引入到核磁共振渗透率模型中，提出了一种新的基于核磁共振的定向渗透率模型并用砂岩和碳酸盐岩岩心进行了分析，所提出的NMR模型不需要对岩石样品进行校准并反映了岩石渗透率的各向异性特征。模型中所需参数的计算较为复杂且需要对岩心进行大量的实验，耗时较长。

(5)

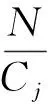
Liu等[19]结合磁共振成像技术，引入局部连通性因子，从成像的角度对SDR模型进行了扩展，估算了渗透率剖面。该方法可将岩心剖面的孔渗特点在二维平面上进行连续表征，运用了不同岩性的岩心进行了处理，样本虽少但证明了所提出的局部连通性的可行性。考虑到相邻地层的连通性，可以沿着井方向对储层非均质性进行适当评估，并可以进一步根据NMR测井数据表征地层渗透率。2个相邻切片的局部渗透率可以定义为：

(6)

白松涛等[20]通过对砂岩T2谱形态的分析提取了定量孔隙结构表征参数，融合了统计学中的正态分布模型和地质混合经验分布模型，进行了渗透率和所提取的表征参数之间相关性研究，该方法可在常规砂岩储层及低孔、低渗储层评价中进行推广应用，由于页岩、碳酸盐岩、火成岩等其他岩石的核磁共振T2谱表征内容及意义与砂岩有所区别，因此基于页岩、碳酸盐岩、火成岩的核磁共振T2谱有待进一步探索和分析，其多学科融合的理念拓展了测井解释在储层评价方面的研究深度和广度。

(7)

式中，φi，max为T2谱中纵向幅度最大的孔隙度分量值；σT2为孔隙分选系数；KG为峰度；T2h为谱峰弛豫时间。

Sun等[21]利用数字岩心技术对不同裂缝参数进行了讨论，引入了一种新的“T2裂缝谱”，研究不同裂缝参数对T2谱的影响。该方法利用数字岩心技术，从三维的角度对裂缝进行分析，其难点在于如何对裂缝进行较为简便的判断。

K=Km[φfcosθ(λT2f)2+1]

(8)

式中，Km为基质渗透率；φf为裂缝孔隙度；T2f为反映裂缝信息的谱，T2f=δ/2ρ2；θ为裂缝倾角；δ为裂缝孔径。

基于几何平均值的渗透率计算方法直接运用核磁共振谱的几何均值建立渗透率计算模型，与核磁共振数据直接联系起来，计算方法较为简单，究其根本，还是SDR模型的改进方法。近年来，随着储层勘探逐渐向低孔渗方向发展，该方法逐渐向复杂储层过渡，如何将不同的孔隙进行区分以及如何以更为简便的方法获取孔隙连通性，成为了该方法如今面临的一大挑战。

2 基于截止值的渗透率计算方法

核磁共振测井可将岩石中的束缚流体与自由流体区分开来，将可动流体与不可动流体进行区分，可据此计算出岩石的渗透率，而区分这2种流体的关键参数就是T2截止值。基于截止值的渗透率计算方法的关键就是如何准确地获取T2截止值。

Timur-Coates模型[22]用孔隙度、束缚水饱和度、自由流体指数来预测渗透率，当束缚水饱和度和孔隙度能够被准确地确定时，这就是一个较常用的方法。该模型主要在中高孔渗的常规储层中计算效果较好，在该模型中，系数的选取[23]以及截止值的准确获取[24-25]都是值得研究的问题。

(9)

式中，FFI为自由流体体积；BVI为束缚流体体积。

李潮流等[26-27]利用了空间物理场分布模型得到了评价了储层中特定尺寸孔隙分布的集中程度的分布系数Q，所提出的集中分布模型可以描述孔隙体积分布的均一性。根据该模型提出了新的渗透率计算方法，可用于分析特低渗透砂岩储层的渗透性，考虑到储层渗透率还受孔隙空间泥质含量及其分布以情况等因素所制约，可以运用多方资料进一步综合研究。

(10)

式中，Swirr为束缚水饱和度。

Smith等[28]提出了使用核磁共振响应来提供无任何外部输入方程，并研究了该方程在页岩与碳酸盐岩储层中的应用。该模型考虑了每种尺寸的孔隙对渗透率的贡献，在实际应用时有着较好的效果，或许在其他不同岩性的储层中也有很好的应用。

(11)

式中，Bphi为粒内孔隙度；wf为相对的弛豫时间权重因子。

李潮流与Smith等所提出的2种方法均是评价了储层中孔隙分布，并据此进行渗透率的计算，此时系数计算对结果产生了重要的影响，若能准确得到系数，这种方法也会得到不错的应用效果。

范宜仁等[29]引入了T2双截止值的概念，将致密砂岩孔隙空间划分为3种：完全可动孔隙、完全束缚孔隙以及部分可动孔隙，并据此提出了渗透率计算的新方法。该方法考虑了不同的岩石孔隙，更好地刻画致密砂岩中流体的赋存状态和渗流规律。T2双截止值的引入为渗透率的计算提供了新的可能性，将SDR模型与Coates模型结合进行考虑，该方法在实际应用中同样存在局限性，其适用于水层或常规油层，气层或稠油层的核磁谱峰形态有较大的差异，导致双截止值计算精度低，渗透率计算不准确。

(12)

式中，Swmd为完全可动流体饱和度；Swird为完全束缚流体饱和度；T2gmd为部分可动流体饱和度信号的几何平均值。

Kwak等[30]利用重水对完全饱水的碳酸盐岩岩心进行驱替，得到了孔隙连通因子，并根据孔隙连通性对Timur-Coates模型进行了修正。通过比较注入重水前后样品的T2分布对孔隙进行了划分，也可通过简单截止值或多个高斯峰拟合方法确定。该研究使用的是简单的临界值法，若使用多重高斯峰拟合方法应提供更准确的连接因子，因为可以更精确地分离重叠的峰区域。在该方法中，孔隙连通性可能会随着注入速率的不同而发生变化，从而影响渗透率的计算。

(13)

式中，P为孔隙连通因子，可判断2个孔隙系统间的连通程度：

Wang等[31]利用纳米材料模拟页岩岩样，将达西定律与泊肃叶方程相结合，对Timur-Coates模型进行了改进，该方法考虑了达西定律与泊肃叶方程，但计算过于繁琐且参数获取困难，较难进行计算。

(14)

式中，D为假设孔隙的表面被束缚水覆盖时束缚水膜的厚度；rt为喉道半径；rb为孔道半径；τ为毛管压力。

基于截止值的渗透率计算方法的关键是利用T2截止值对孔隙的连通性进行划分，该方法中，经典的Timur-Coates模型常用于中、高孔渗的常规砂岩储层，随着储层复杂化，仅用单一的T2截止值已经无法对孔隙连通性作出较好评价，有学者提出的双截止值法在致密砂岩储层渗透率计算中有着较好的运用，相较于常规的方法能更好地刻画致密砂岩中流体的赋存状态和渗流规律，该方法可能会成为基于截止值的渗透率计算方法下一步研究的方向。

3 复合方法

除上文提到的根据核磁共振数据直接进行计算的两种核磁渗透率计算方法外，国内外众多学者还提出了许多复合的核磁渗透率计算方法，将不同的方法与核磁共振岩心实验数据相结合，以达到更加准确地获取核磁共振渗透率的目的。Swanson参数法[32-33]将T2谱与毛管力数据结合计算出Swanson参数，再根据Swanson参数与储层物性参数的关系进行渗透率的求取。孔喉半径转换法[34-41]结合压汞实验与核磁共振岩心实验数据，将岩心的T2gm与孔喉半径进行转换后，建立孔喉半径与渗透率之间的计算关系，从而计算出储层的渗透率。流动单元指数(FZI)法[42-45]基于核磁共振数据对流动单元进行刻度，并根据岩心流动单元指数的差异，将岩心样品划分为不同的类型，将同一类型的岩心进行孔隙度与渗透率的相关性分析，从而对岩石渗透率进行估算。孔隙贡献法[46-49]将T2谱划分成不同的区间以反映不同的孔隙类型，得到不同类型孔隙对渗透率的贡献，用以计算出储层的渗透率。这4种方法的核心是根据岩心孔径差异进行分类后，对每一类型岩心的核磁渗透率进行计算，在目前低孔低渗的储层中有着较好的应用效果。人工智能法[50-55]结合当下热门的人工智能技术，采取不同的算法对核磁共振数据进行处理并建立了核磁渗透率计算模型，该方法需要大量的岩心数据作为样本，在岩心数据较少时应用效果较差。Xiao等[56-57]分析了2个致密砂岩储层压汞毛细管压力(MICP)和核磁共振(NMR)实验数据，对前人提出的SDR模型、Timur-Coates模型、Swanson参数法等进行了比较分析，讨论了各方法的优劣。Swanson参数法在致密砂岩储层中的应用效果要优于经典的SDR模型与Timur-Coates模型，该模型充分考虑了孔隙结构信息，可用于致密砂岩渗透率的精确估算。

复合方法在低孔、低渗的非常规储层中应用较为广泛，该方法将不同的方法与核磁共振数据相结合，考虑了孔隙结构信息对储层渗透率的影响，在一定程度上提高了核磁渗透率计算的准确性。将不同的方法与核磁共振数据结合起来，可以弥补核磁共振数据无法表征孔隙连通性的缺点，更加适用于如今低孔、低渗的非常规储层的渗透率计算。

4 结论与认识

在油气储层评价中渗透率是关键参数之一，准确获取储层渗透率对油气藏勘探开发有着重要作用。核磁共振测井技术以其特有的优点，能够较为准确地获取储层渗透率，国内外学者在此方面进行了大量的研究。随着各个方法的提出与应用，核磁共振渗透率计算方法从最经典的SDR模型与Timur-Coates模型逐渐发展到如今多种模型并驾齐驱，从最初的只能应用于常规地层到如今的复杂储层的应用，核磁共振渗透率计算方法的广泛应用证实了核磁渗透率的有效性，为特殊、复杂储层的评价提供了新的思路。

本文对根据不同的核磁渗透率计算方法进行归纳总结，将核磁渗透率计算方法分为3类：①基于几何平均值的渗透率计算方法；②基于截止值的渗透率计算方法；③复合方法。究其根本，仍是对经典的SDR模型与Timur-Coates模型的改进与应用，使其在复杂储层中得到较好的应用。

目前核磁共振储层渗透率计算方法向着双截止值、多孔隙贡献等方向发展，其主要问题在于复杂储层孔隙连通性的判定，运用不同的方法对储层孔隙的连通性以及孔径尺寸分布进行划分评价并据此对核磁渗透率进行计算，成为了目前的一大趋势。许多方法具有特殊性、唯一性，在不同储层条件下的应用效果还需进一步研究。总的来说，不同的方法互相结合，为储层核磁共振渗透率的计算提供了新的发展方向。