地铁列车延误情况下乘客可容忍候车时间预测模型
王镇波,叶霞飞,王 治
(1.同济大学道路与交通工程教育部重点实验室,上海 201804;2.同济大学上海市轨道交通结构耐久与系统安全重点实验室,上海 201804)
地铁列车延误发生后,不可避免地会对乘客出行产生一定影响。一部分乘客会在站台原地等待后续列车,若不及时采取客流疏导,时间一长站台便容易出现拥挤,产生许多安全隐患;一部分乘客会更改其在城市轨道交通系统内的出行路径,虽然避免了在站台集聚,但却对途经的非原路径区段造成了额外的客流负担,使得拥挤风险加剧;还有一部分乘客会离开城市轨道交通系统改用其他交通方式出行,对道路交通产生了一定的压力。造成上述乘客出行行为差异的一个关键原因,便是乘客对于候车时间的忍耐程度不尽相同。因此,合理预测不同类型乘客可容忍候车时间,对突发事件下的乘客路径选择行为预测、客流诱导和疏散对策制定等方面均具有重要意义。
目前国内确定乘客可容忍候车时间的方法虽然已经从最初的分类统计进行规律总结[1],逐渐深化到了概率分布拟合[2-3],但并未在拟合的概率分布中考虑影响因素,这使得构建的模型难以用于预测。国外在这方面则有所突破,近年已有学者[4-5]基于生存分析构建了考虑影响因素的概率分布模型,并取得了较好的预测效果。
生存分析是生物统计研究领域的热点,主要研究观测对象的生存状态[6],如某种症状的发生时间及在任意时刻发生症状的风险大小。生存分析的因变量为生存时间,属于连续型变量,可以广泛地定义为从规定的观测起点到发生某一给定终点事件的时间[7]。因此,生存分析在交通领域已有一定应用,如预测交通事故持续时间[8]、非机动车越线超车行为持续时间[9]等。如果将乘客进入站台开始候车作为观测起点,因等待过久而失去耐心选择出站作为终点事件,则乘客在此期间的候车时间可定义为生存时间,其可容忍候车时间便是离开站台时已等待的时间,由此可引入生存分析理论。
考虑到列车延误发生后,乘客普遍优先重视出行时间[2],且难以获知准确的列车延误持续时间[3],因此在可接受的出行时间范围内,相比于在站台原地等待或直接出站选择其他交通方式,乘客往往会青睐行程时间更容易把握的在系统内绕行。为此,本文将无法获知准确列车延误持续时间,且在系统内绕行路径不可行的乘客作为研究对象,引入生存分析理论,构建了考虑个人属性、出行特征等影响因素的该类乘客可容忍候车时间预测模型,并用调查数据对模型进行标定与检验,以期为非正常运营情况下地铁乘客出行行为方面研究的深化提供新思路。
1 基于生存分析的乘客可容忍候车时间预测模型构建
1.1 生存分析核心理论
生存分析用于研究观测对象从规定的观测起点到发生给定终点事件可能经历的时间,观测对象在此期间标记为存活状态,这段时间定义为生存时间T,为连续型非负随机变量。则观测对象生存时间T超过给定时间t的概率S(t)为
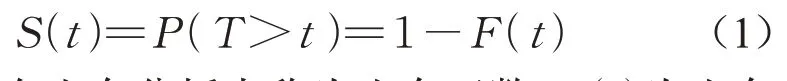
式中:S(t)在生存分析中称为生存函数;F(t)为生存时间T的分布函数,表示观测对象生存时间T不超过时间t的概率。
若观测对象在时间t处于存活状态,则会相应地计算该观测对象在t到t+△t这一极小时间区间内发生终点事件的可能程度h(t),即:
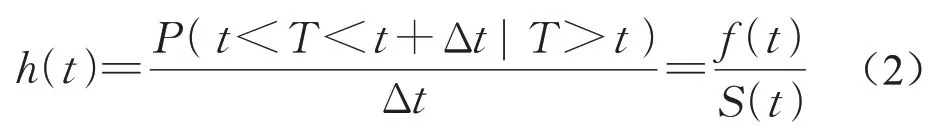
式中:h(t)在生存分析中称为风险函数,也可理解为在时间t仍存活的观测对象将发生终点事件的条件概率密度;f(t)为生存时间T的概率密度函数;S(t)为生存时间T的生存函数。
生存分析主要讨论风险函数h(t)受协变量影响的情况[6]。
1.2 基于生存分析的乘客可容忍候车时间预测模型
将乘客进入站台开始候车作为观测起点,因等待过久而失去耐心选择出站作为终点事件,则乘客在此期间的候车时间可定义为生存时间,其可容忍候车时间便是离开站台时已等待的时间。
为了得到可容忍候车时间的具体分布并建立可容忍候车时间与各影响因素之间的量化关系,本文选择构建生存分析参数模型,这方面常用的模型有比例风险模型和加速失效时间模型。比例风险模型构造的风险函数与协变量回归方程[8]为
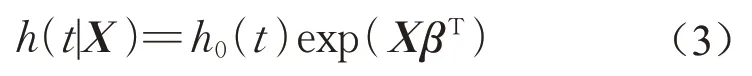
式中:h0(t)称为基准风险函数,指没有任何因素影响下观测对象在时间t的基础风险,即h(t|X=0),其函数形式根据假定生存时间服从的概率分布确定;X=(x1,x2,…,xn)和β=(β1,β2,…,βn)分别为协变量和回归系数向量;n为协变量个数。
加速失效时间模型构造的风险函数与协变量回归方程[4]为
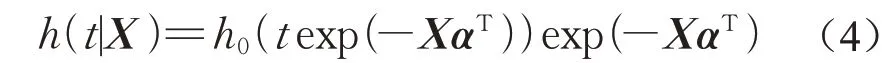
式中:观测对象在时间t的基础风险为h0(texp(-XαT)),相当于将时间t调整了exp(-XαT)倍,由此得名加速失效时间模型;X=(x1,x2,…,xn)和α=(α1,α2,…,αn)分别为协变量和回归系数向量;n为协变量个数。
至于是选择比例风险模型还是加速失效时间模型,应根据所研究对象发生终点事件的风险特点先合理假定生存时间服从的概率分布,若该概率分布只适用于其中一种模型,则无需做选择;若都适用,此时这两种模型的预测结果一致且彼此的回归系数存在相互转换关系[10],可任意选择。
目前既有文献[4-9]在构建生存分析参数模型时,均假定生存时间服从多个概率分布,常用的有指数分布、Weibull分布、对数正态分布、对数logistic分布,通过比较拟合效果从中选择最佳者。但由于各个概率分布的风险函数特性存在差异[10](图1),故在确定备选概率分布时,应首先分析研究对象在不同时间发生终点事件的特征,之后再去选择风险函数变化趋势符合该特征的概率分布。
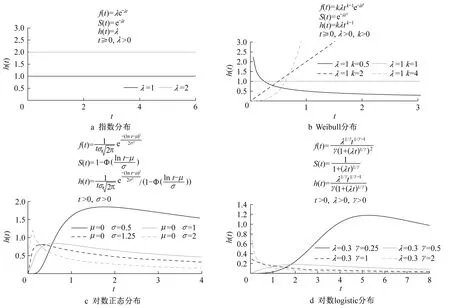
图1 生存分析参数模型常用概率分布的风险函数Fig.1 Hazard functions of commonly used probability distributions in survival analysis
本文的研究对象乘客无法获知准确列车延误持续时间,使得其难以确定最终等到列车需要花费的总时间,而一直在站台原地等待又会使整个行程的耗时不断增加,因此已投入的候车时间越长,乘客越容易出现焦躁与不安情绪,放弃继续等待而出站选择其他交通方式,从而及时控制整个行程耗时的可能性就越高。这意味着随着候车时间增加,乘客放弃等待而选择出站的意愿也在增加,即发生终点事件的风险在不断增加。根据图1可知,只有Weibull分布的风险函数可以在形状参数k>1时符合这一特征,因此本文选择Weibull分布进行后续建模。
由于Weibull分布的形状参数k决定了分布变化趋势,故通常作为待估计常数,不与协变量构建回归方程[7-8]。在这个前提下,可令基准风险函数h0(t)=cktk-1,c>0,分别构建比例风险模型和加速失效时间模型。
如果构建比例风险模型,根据式(3)及Weibull分布的风险函数h(t)=kλtk-1、基准风险函数h0(t)=cktk-1可得到λ=exp(XβT+β0),其中截距β0=lnc。
如果构建加速失效时间模型,根据式(4)及Weibull分布的风险函数h(t)=kλtk-1、基准风险函数h0(t)=cktk-1,首先可得到kλtk-1=ck(exp(-XαT)t)k-1exp(-XαT)=ckexp(-k XαT)tk-1,从而得到λ=exp(-k(XαT+α0)),其中截距α0=-lnc/k。则回归系数向量β和α、截距β0和α0的数值转换关系分别为β=-kα、β0=-kα0。
综上所述,本文基于生存分析最终构建的乘客可容忍候车时间预测模型为

式中:T为乘客可容忍候车时间;S(t)、f(t)分别对应生存函数和概率密度函数;X为影响乘客可容忍候车时间的因素所组成的协变量向量;k为形状参数,为了符合风险函数值随候车时间增加而增加的特点,需满足k>1;λ为尺度参数,有两种回归方程可供选择;β和β0、α和α0为相应的回归系数向量和截距,β=-kα,β0=-kα0。
模型中的参数通过极大似然估计法确定。对于乘客样本{ti,Xi,δi},i=1,2,…,m,模型的似然函数为
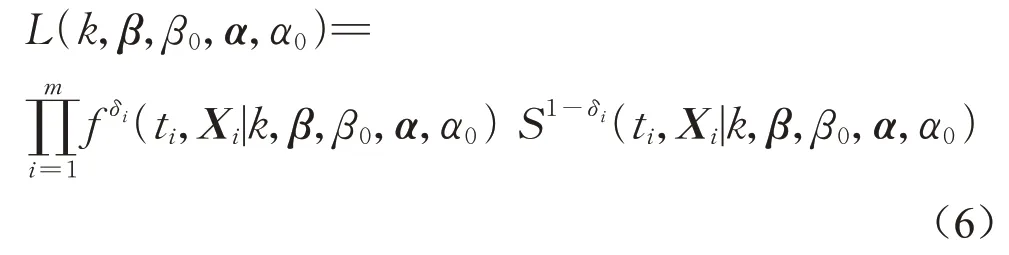
式中:ti为乘客i在观测期间的候车时间;Xi为乘客i的可容忍候车时间影响因素的属性值向量;δi为乘客i的状态变量,若观测结束时仍在站台原地候车则δi=0,否则δi=1;m为乘客样本数。
2 数据来源
为获知乘客年龄、出行目的等体现个体差异性[2]的信息,本文采取RP(revealed preference)和SP(stated preference)混合问卷调查获取相关数据。
2.1 问卷设计
在综合参考既有文献[1,3,5,11-13]调查问卷的基础上,本文从乘客个人属性、平时出行特征、模拟情景下出行特征这三个方面设计问卷所需要调查的内容。
乘客个人属性和平时出行特征属于RP调查,主要获取体现乘客个体差异性的信息。乘客个人属性涉及4项调查内容:性别、年龄、职业、月收入。平时出行特征涉及7项调查内容:主要乘坐地铁出行所在城市、每周地铁使用频率、乘坐地铁主要出行目的、乘坐地铁主要出行时段、地铁全程耗时(进站到出站)、选择地铁出行时为整个行程预留的时间、实际遭遇列车晚点经历。其中,职业、实际遭遇列车晚点经历主要为无效问卷的筛选提供辅助信息,后续不作为潜在影响因素考虑。
模拟情景下出行特征属于SP调查,主要调查乘客在不同出行情景下可容忍候车时间偏好。模拟情景设定被调查者现在进行一次以地铁为主方式的出行,预计地铁全程耗时为20/30/40/50/60 min,出行目的、出行时段、为整个行程预留的时间与平时出行特征一致,在站台候车时被告知列车晚点且持续时间不明,从而询问被调查者在这种情况下可容忍候车时间(一旦超过该时间便会直接出站选择其他交通方式)。每位被调查者可得到5组数据,彼此因模拟情景不同而具有独立性。
2.2 问卷调查情况
本文借助问卷星平台采取网络问卷的形式进行调查,调查时间为2021年3月1日至14日,共收集主要乘坐地铁出行所在城市填写了上海的问卷932份。在此基础上进行无效问卷剔除,共计65份,具体涉及部分属性(职业、年龄、月收入、乘坐地铁主要出行目的)之间存在正常逻辑冲突的问卷28份、填写时间过短的问卷7份、实际列车晚点经历下在站台原地候车时间大于对照模拟情景下可容忍候车时间的问卷30份。最终得到的有效问卷数为867份,在0.05显著性水平下符合抽样样本数要求[14]。
乘客个人属性、平时出行特征方面,调查数据的男女比接近1:1;年龄分布占比最高的是23~30岁,为43.8%;职业以企事业人员为主,占74.1%;月收入分布中10 001~20 000元的占比最高,为28.0%;主要乘坐地铁出行所在城市均为上海;每周地铁使用频率占比最高的是5 d,为34.3%;乘坐地铁主要出行目的以上下班为主,占65.2%;主要在早、晚高峰乘坐地铁出行的比例为68.4%;地铁全程耗时在31~40 min的占比最高,为27.5%;选择地铁出行时为整个行程预留的时间在6~10 min的占比最高,为38.4%,且预留时间在15 min以内的比例达到75.0%;39.9%的被调查者曾经历列车晚点,在站台等待是最普遍的选择。具体统计结果如表1所示。
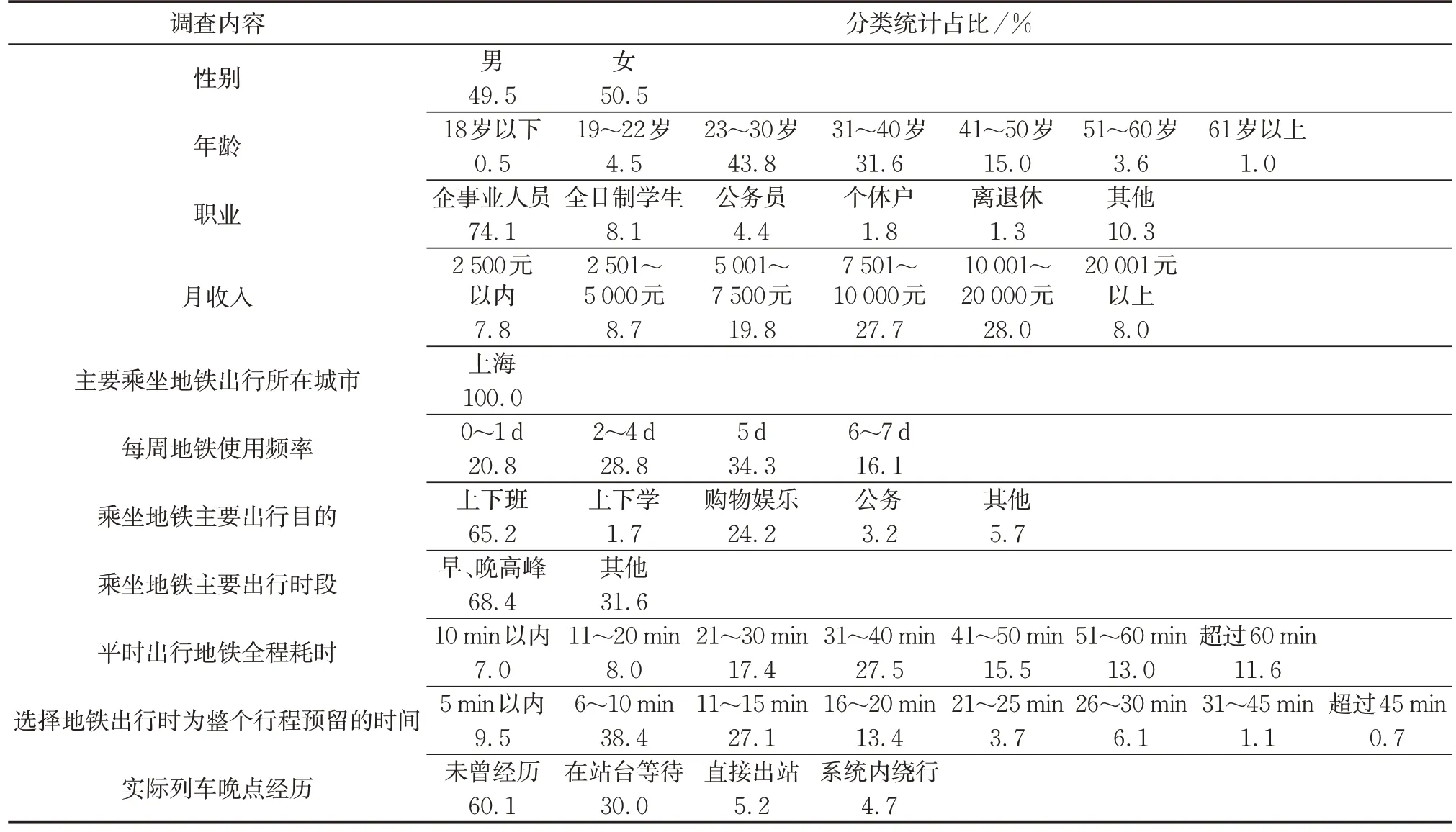
表1 乘客个人属性、平时出行特征统计结果Tab.1 Descriptive statistics of RP survey
模拟情景下出行特征方面,随着地铁全程耗时的增加,乘客可容忍候车时间呈现了总体增加的趋势,其中15 min以内的占比始终高于68%,如图2所示。这一方面反映了地铁全程耗时对乘客可容忍候车时间的影响特点,另一方面揭示了乘客可容忍候车时间的主要分布趋势。
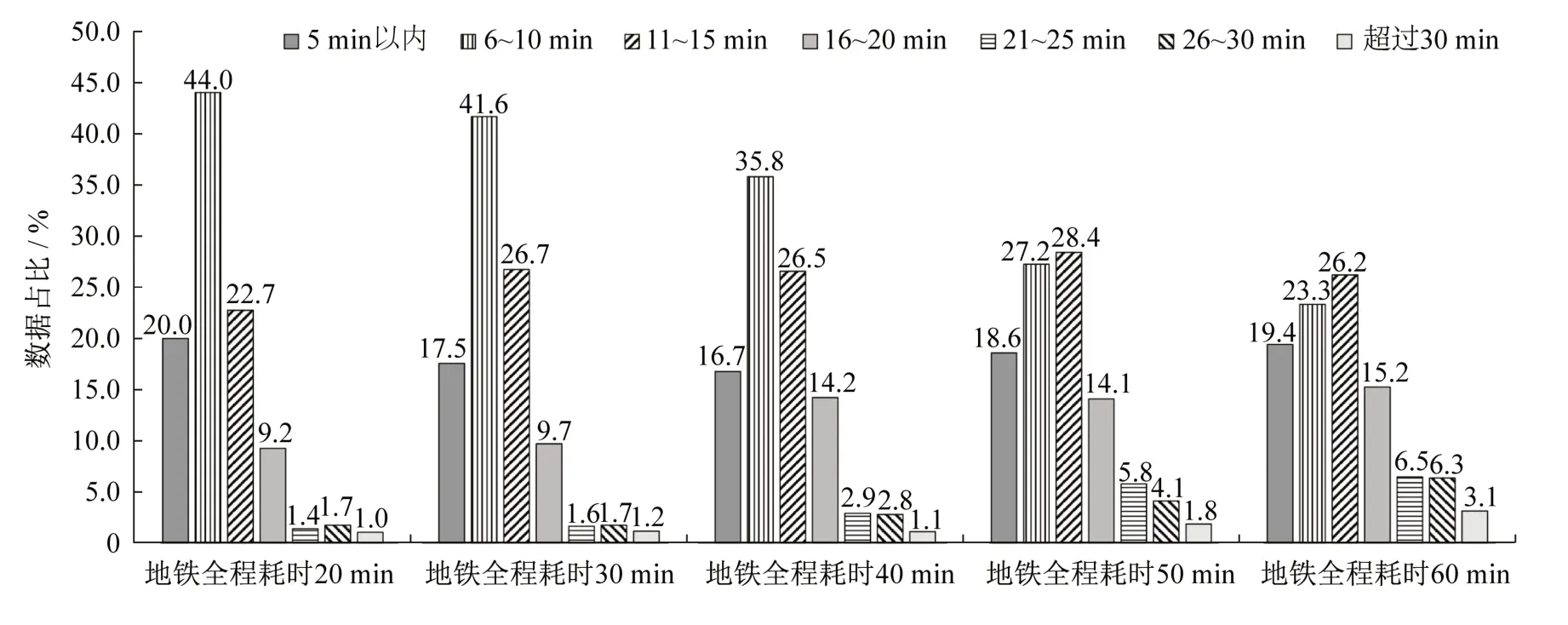
图2 不同地铁全程耗时模拟情景下乘客可容忍候车时间的分布Fig.2 Distributions of passenger tolerable waiting time under different metro travel time scenarios
3 模型标定与检验
3.1 数据集生成
对上述问卷调查获得的定量和定性数据进行赋值,从而生成模型用数据集。其中,涉及时间的变量均转化为连续型变量,无序分类变量尽量将特点相近的分类归在一起,以减少哑元变量的引入,如出行目的中上下班和上下学有硬性到达时间要求,可同属一类,其他出行目的则另属一类。各变量的定义及赋值说明如表2所示。
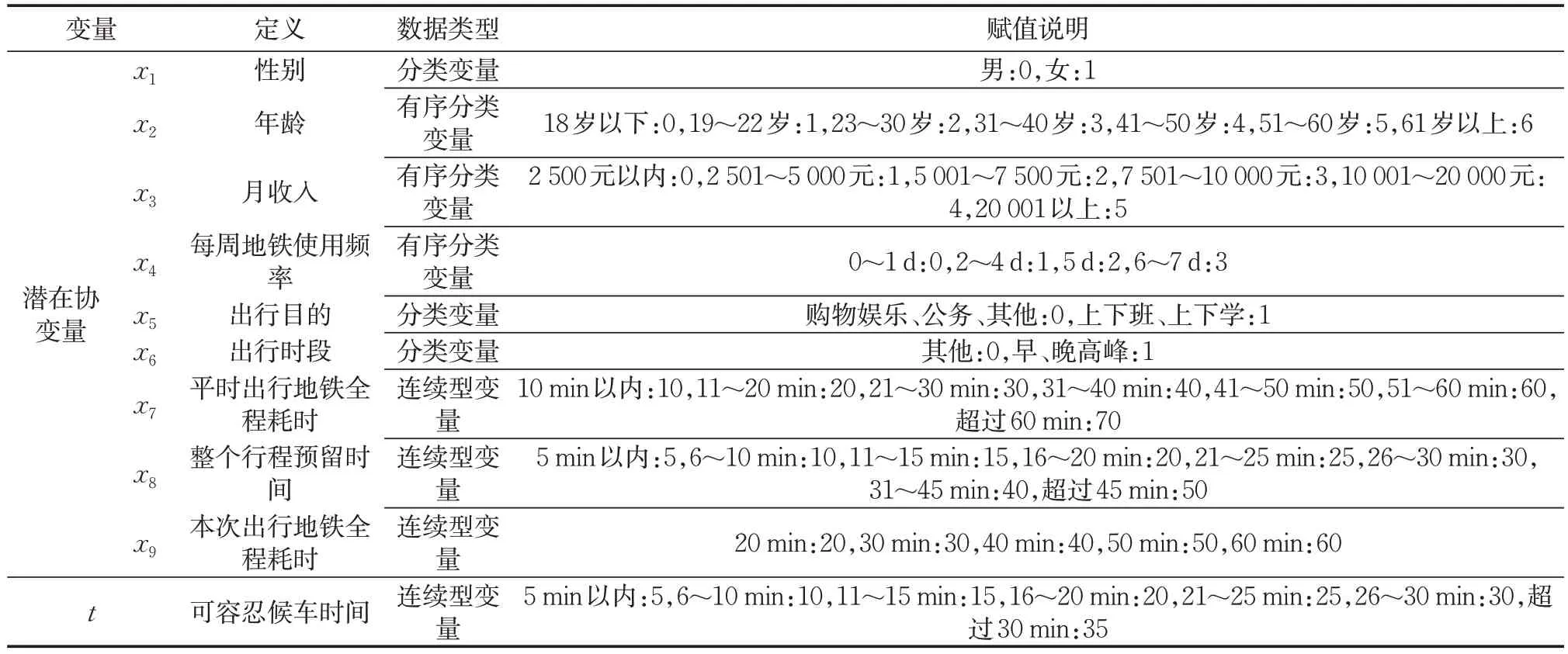
表2 变量定义及赋值一览Tab.2 Summary of variable definition and assignment
由于一个被调查者会得到5组不同地铁全程耗时出行情景下可容忍候车时间数据(每组数据x1至x8相同,x9、t存在差异),故最终生成的数据集共有4 335个乘客样本。
3.2 系数标定与检验
可容忍候车时间相当于观测结束时已经出站乘客的候车时间,即每个乘客的状态变量δ均为1,回归方程选择λ=exp(XβT+β0)以便于参数标定,则似然函数可由式(6)变为
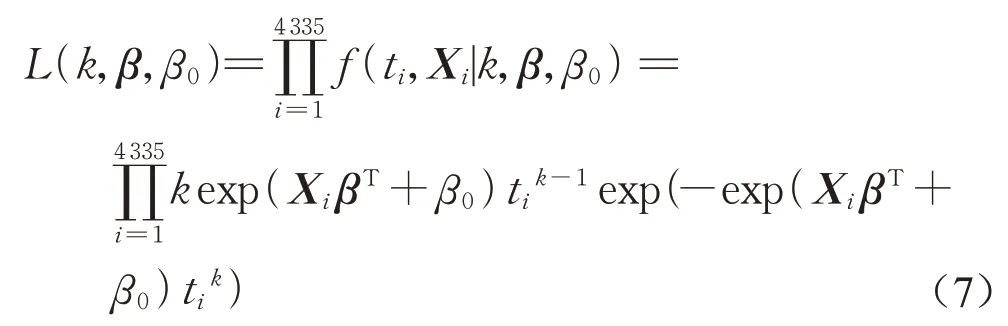
采用向后逐步回归法对潜在协变量进行筛选及极大似然估计,显著性水平取0.05,具体计算过程由Stata数据分析软件完成,最终的协变量筛选及参数估计结果如表3所示。
从表3可知,模型的形状参数k大于1,既满足了参数取值要求,也验证了乘客放弃等待而选择出站的意愿会随候车时间增加而增加的特点。最后共有5个协变量通过显著性检验:每周地铁使用频率x4的系数为负,说明出行依赖地铁的程度越高,出站意愿越低,可容忍候车时间越长;出行目的x5的系数为正,说明上下班、上下学相比于购物娱乐等其他出行目的,出站意愿更高,可容忍候车时间更短;平时出行地铁全程耗时x7的系数为负,说明平时习惯的地铁出行距离越长,出站意愿更低,可容忍候车时间更长;整个行程预留时间x8的系数为负,说明为出行过程中接驳、换乘等准备的弹性时间越多,出站意愿越低,可容忍候车时间越长;本次出行地铁全程耗时x9的系数为负,说明长距离地铁出行相比于短距离地铁出行,出站意愿更低,可容忍候车时间更长。
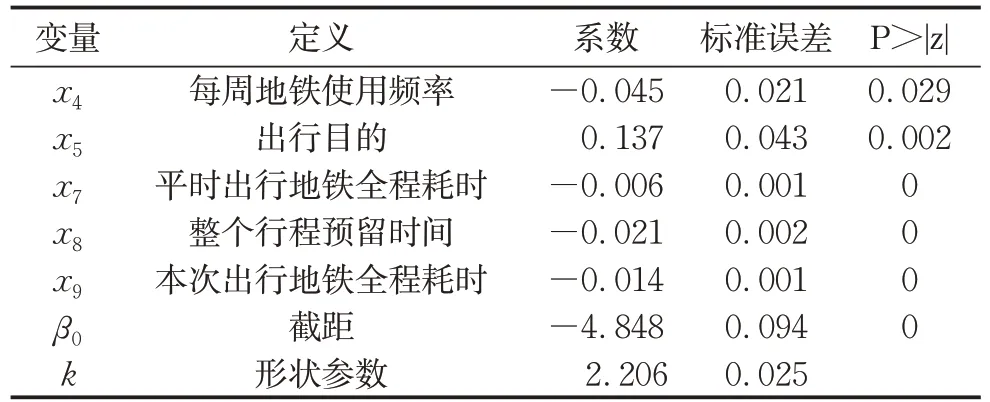
表3 模型估计结果Tab.3 Estimated results of the model
最终标定得到的地铁列车延误情况下乘客可容忍候车时间预测模型为
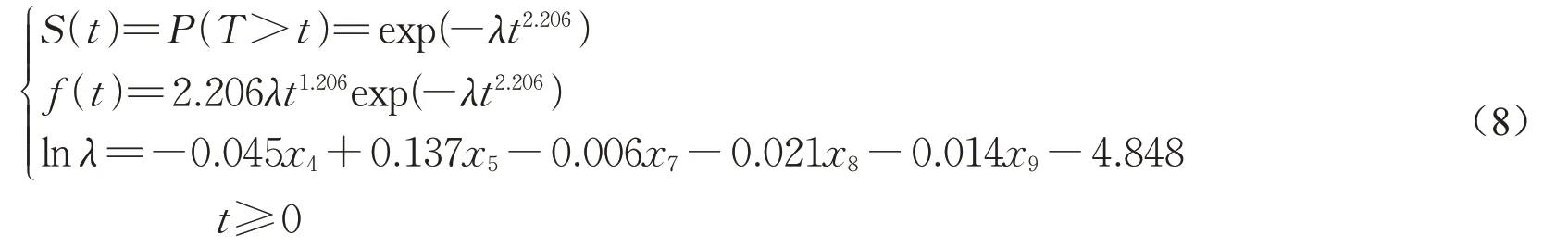
式中:T为乘客可容忍候车时间;x4、x5、x7、x8、x9分别为乘客的每周地铁使用频率、出行目的、平时出行地铁全程耗时、整个行程预留时间、本次出行地铁全程耗时,取值详见表2。
3.3 结果讨论
考虑到每种协变量组合均会生成不同的生存函数曲线,难以逐一比较并分析,本文选择将每周地铁使用频率为5 d(x4=2)、出行目的为上下班(x5=1)、整个行程预留时间为10 min(x8=10),每次出行地铁全程耗时稳定(平时出行地铁全程耗时x7为本次出行地铁全程耗时x9为10/20/30/40/50/60 min)的日常地铁上下班乘客作为对象,对其可容忍候车时间进行结果讨论,以便为早晚高峰地铁运营延误发生后的应急处理方案的选择提供时限参考。将上述协变量组合代入式(8)计算得到的生存函数如图3所示。
从图3可知,随着地铁全程耗时的增加,生存函数整体在向右上方靠近,说明可容忍候车时间总体在增加。生存函数S(t)=0.8最早出现在5.4 min,地铁全程耗时10 min与60 min的中位可容忍候车时间分别为9.0 min与14.3 min,说明此类乘客可容忍候车时间在5.4 min以上的概率高于80%,但超过14.3 min的概率低于50%。因此,当早晚高峰地铁运营延误发生后,运营方在选择应急处理方案时(如调整列车开行方案、安排应急接运公交等)应尽量避免超过14.3 min才恢复运营,最佳时间为5.4 min以内。
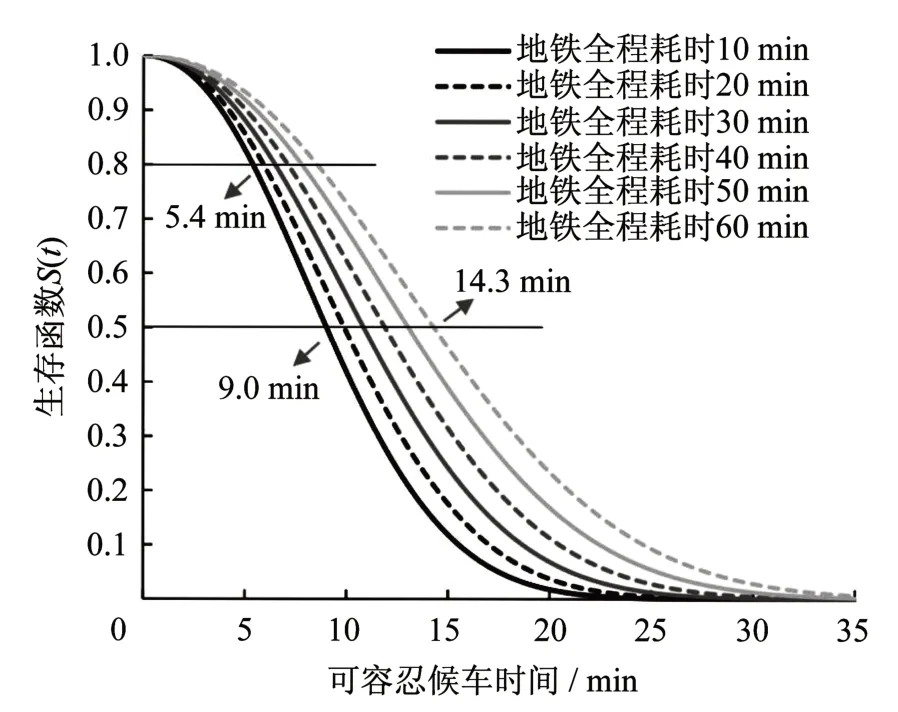
图3 日常地铁上下班乘客可容忍候车时间的生存函数Fig.3 Survival functions of tolerable waiting time of metro-oriented commuters
4 结论
本文以无法获知准确列车延误持续时间,且在系统内绕行路径不可行的乘客为研究对象,基于生存分析理论构建了这类乘客在个人属性、出行特征等影响因素下的可容忍候车时间预测模型,主要结论如下:
(1)本文的研究对象乘客具有因等待过久而失去耐心选择出站的意愿随候车时间增加而增加的特点,为此在构建生存分析参数模型时应选择Weibull分布。基于Weibull分布的比例风险模型和加速失效时间模型可相互转换,因此最终的预测模型对两者进行了整合。
(2)基于RP和SP混合问卷调查获得的数据挑选潜在协变量并标定模型,结果表明:乘客可容忍候车时间与每周地铁使用频率、平时出行地铁全程耗时、整个行程预留时间、本次出行地铁全程耗时显著正相关;乘客上下班、上下学时可容忍候车时间小于购物娱乐等其他出行目的。
(3)根据模型预测结果,日常地铁上下班乘客可容忍候车时间在5.4 min以上的概率高于80%,但超过14.3 min的概率低于50%,可为早晚高峰地铁运营延误发生后的应急处理方案的选择提供时限参考。
该模型可为预测列车延误情况下不同乘客的可容忍候车时间提供有效方法,有利于深化非正常运营情况下地铁乘客出行行为方面的研究。后续进一步的研究工作是补充更多城市的乘客数据集进行模型推广,更深入客观地从中挖掘显著影响因素及其影响规律。
作者贡献声明:
王镇波:数据分析,模型构建。
叶霞飞:理论框架搭建,论文修改指导。
王治:问卷设计,论文核心结论提炼。

