基于改进启发式蚁群算法的无人机自主航迹规划

辛建霖，左家亮，岳龙飞，张宏宏

（空军工程大学 空管领航学院，西安 710051）

0 引 言

随着科学技术的发展，现代战争信息化、智能化程度逐渐提高，使得无人机的应用发展受到更多关注。无人机航迹规划是无人机作战应用的关键环节，其目的是在满足各种约束条件的前提下（无人机性能、飞行安全性、任务目标等），寻找到一条最优或较优航迹。航迹规划经历了从手动绘制到计算机自动解算两个阶段，研究内容主要包括：地形和威胁等环境要素的表示方法分析、基于任务需求的目标函数构造、满足飞行距离和转弯半径等限制因素的约束条件处理、针对实时性和协同性等需求的航迹搜索算法研究。现有的航迹规划已可以满足一定的应用需求，例如，田疆等提出了一种改进连接型快速扩展随机树算法，可用于复杂环境下的无人机三维航迹规划，但在实时性、高效性、协同航迹规划和可替换航迹规划等方面仍然存在一些不足。

航迹规划算法主要分为两大类，一类是经典算法，如最优控制法、动态规划法等；另一类是智能算法，如人工势场法、粒子群算法、遗传算法、蚁群算法等。最优控制法把航迹规划问题转化为最优控制问题，建立最优控制模型进行求解，但这种方法对初始值要求较高，建模和求解较为复杂。遗传算法模拟生物遗传进化过程，求解航迹规划问题高效、鲁棒性强，但算法容易早熟收敛，局部搜索能力较差。李涵等在歼轰机突防突击过程中，运用改进的遗传算法进行了航线规划，但其计算模型考虑因素较少，模型尚不完善。蚁群算法（Ant Colony Algorithm，简称ACO）是一种基于对蚂蚁群体觅食行为的研究而提出的搜索算法，具有鲁棒性好、正反馈能力强的优点，但面对复杂问题时，容易出现算法停滞、陷入局部最优、运算时间过长等问题。为此，国内外对ACO 算法提出了许多改进措施。陈雄等对信息素挥发系数进行动态调整，用优化参数的方式有效解决了算法停滞的问题，但改进后算法不够灵活；B. Bulln⁃heimer 等引入精英蚂蚁策略，通过改进算法结构提高最优和次优路径的引导能力，但收敛速度较慢；Wang L 等采用融合遗传算法的方式提升ACO 算法的寻优能力，但算法适应性较差。

本文提出一种改进启发式蚁群算法（Im⁃proved Heuristic Ant Colony Algorithm，简称IHACO）的无人机自主航迹规划算法，通过引入Dijk⁃stra 算法、Logistic 混沌映射、多航迹选择策略、模拟退火机制的方法对ACO 算法进行改进，以提高算法初期的搜索效率，增强全局寻优能力，平衡收敛速度与全局寻优能力之间的矛盾，增强算法在复杂环境中的搜索性能，并对算法进行仿真分析。

1 航迹规划问题描述及环境建模

1.1 问题描述

针对无人机在作战任务中穿越地形障碍、躲避敌方地对空导弹威胁的航迹规划，简化运行环境并进行如下假设：（1）简化模型，将无人机简化为质点；（2）假设无人机在执行任务中，保持一定的飞行高度和速度，在二维有限空间进行移动；（3）假设地形障碍、地空导弹火力覆盖范围已知，并用多边形进行表示（通常地空导弹火力覆盖为圆形区，这里简化模型，用正方形区域表示）。

1.2 空间建模

在航迹规划中，常用的空间建模方法有VOR⁃ONOI 法、栅格图法、链接图法等，其中链接图法具有简化模型占用内存少、效果好的优点，故本文采用链接图法构造二维空间模型，生成规划可用空间，如图1 所示，在MATLAB 环境中构造200 km×200 km 的二维空间，存在4 个不规则多边形表示的障碍区域、多条自由链接线（黑色虚线表示）和初始点和终止点，链接各链接线中点、初始点和终止点，生成初始航迹规划网络图（黑色实线表示）。

图1 链接图法构造二维空间模型图Fig.1 Construction of two dimensional space model graph by link graph method

1.3 航迹点的构造

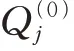
式中：h为比例参数；为与航迹相交的链接线数。

通过式（1）可知，用，，…，h，和可以表示一条从起始点到终止点的航迹。

1.4 建立目标函数

在无人机飞行穿越地形障碍、躲避敌方地对空导弹威胁时需要进行航迹规划，航迹规划的任务是根据起始点和目标点的位置，在避开地形障碍区、导弹威胁区的前提下，找到一条最短航迹，保证无人机能够安全、快速通过。目标函数为

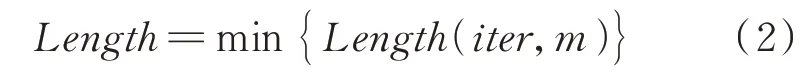
式中：(，)为航迹长度（在第次迭代第只蚂蚁的情况）。

2 蚁群算法改进

2.1 Dijkstra 算法规划初始航迹

为了改善ACO 算法前期搜索效率差的问题，运用典型的最短路径算法，在算法求解出一个节点到其他节点的最短航迹的基础上，确定起始点到终止点的一条较优航迹，以减少ACO 算法前期搜索的盲目性。Dijkstra 算法的基本思想是先把二维模型中的节点分为两组，一组为已确定最短航迹的节点，另一组为未确定最短航迹的节点，按最短航迹长度递增的顺序逐个把未确定的节点加入已确定的一组中，直到所有节点都成为已确定的节点，即可得到一条从初始点到终止点的较优航迹。Dijkstra 算法流程如图2 所示。

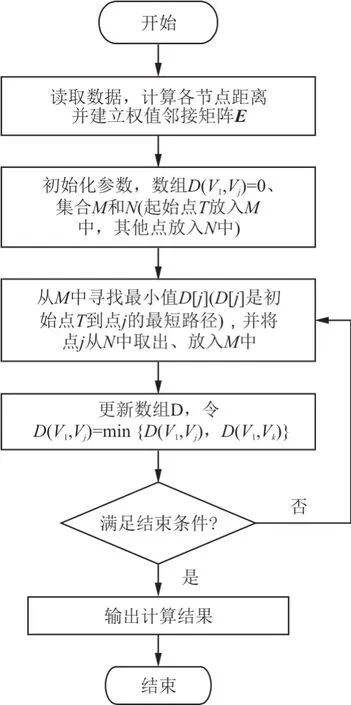
图2 Dijkstra 算法初始化航迹流程图［20］Fig.2 Flow chart of Dijkstra algorithm initialization track［20］

2.2 引入Logistic 混沌映射初始化信息素

为了避免蚁群停滞在局部搜索，提高算法收敛速度，引入混沌扰动。混沌是在确定性系统中存在的随机情况，表现为类似随机的非随机运动现象，其具有规律性、遍历性、随机性等特点。本文在初始化信息素阶段应用Logistic 混沌映射。Logistic 混沌映射方程：

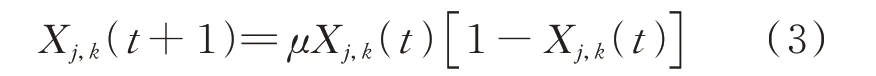
式中：X()为混沌变量；为控制变量。

当=4，0 ≤X(0)≤1 时，式（3）处 于 混 沌状态。

信息素中引入Logistic 混沌映射：

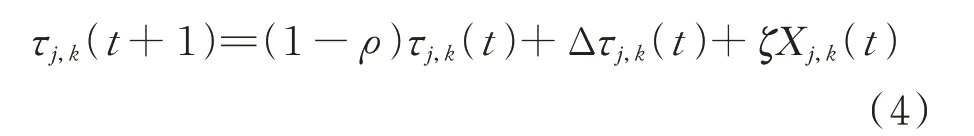
式中：为可调节参数。

2.3 多航迹选择策略

在ACO 算法中，状态转移规则直接影响了搜索解的质量和效率，将真实蚂蚁在前进中对信息素利用、对新航迹的探索以及一些“随机行为”引入状态转移规则，采用多航迹选择策略对基本状态转移规则进行改进，公式为

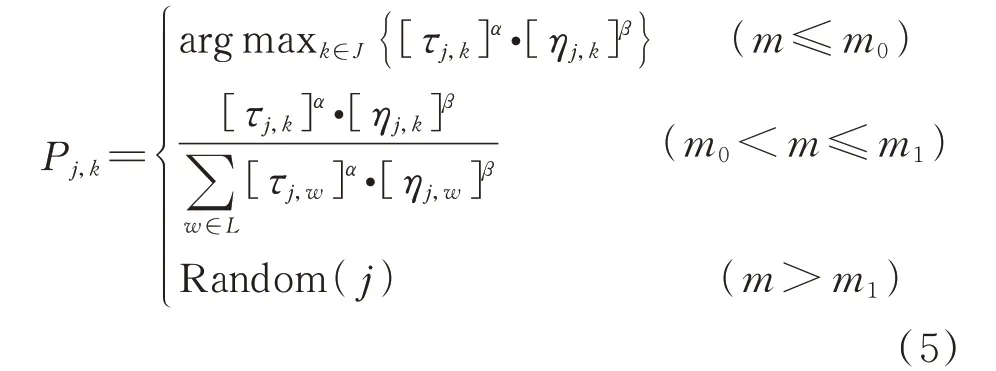
式 中：，为 常 数 且0 ＜＜1，0 ＜＜1；为随机数且0 ＜＜1。

当≤时，从 可 行 航 迹 点 中 找 出[τ]·[η]最 大 的 航 迹 点；当＜≤时，使 用ACO 算法的状态转移规则选择航迹点；当＞时，随机选择下一个航迹点。这种设计很好地保证了解的多样性，同时避免算法因收敛速度快而陷入局部最优的情况。

2.4 模拟退火算法

Metropolis 研究发现一般组合优化问题和固体物质退火过程中物理系统的能量变化具有相似性，进而提出了模拟退火优化算法。固体物质退火分为升温、等温、降温三个阶段，高温阶段固体升温，内能增加，固体内的粒子无序运动速度快，此过程与算法设置的初始温度对应；等温阶段固体与外界保持热平衡状态，此过程与算法设置Me⁃tropolis 抽样准则对应；退火阶段固体温度降低、内能减小，粒子趋于有序，最终达到稳定状态，此过程与算法控制参数减小相对应。使用Metropolis抽样准则接受一定条件下的劣解，有效避免陷入局部最优，以达到收敛全局最优解的效果。模拟退火算法流程如下：

（1）初始化：设置系统温度为，初始温度(0)=，任取初始解，确定每个时的迭代次数，即Metropolis 链长。

（2）对当前温度和=1，2，…，，重复步骤（3）～步骤（6）。

（3）对当前解进行随机扰动，得到新解；

（4）设置增 量 为d，d=()-()，为的代价函数。

（5）根据Metropolis 准则，公式为

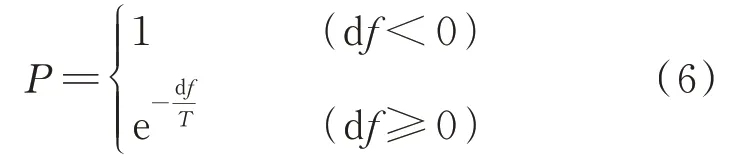
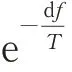
（6）当连续多个Metropolis 链中都未接受新解，或退火达到终止温度，输出当前解为最优解，然后结束；否则减小温度后返回步骤（2）。

2.5 算法步骤

IH-ACO 算法通过Dijkstra 算法初始航迹、Lo⁃gistic 混沌映射初始化信息素、采用多航迹选择策略和模拟退火机制，在提高算法收敛速度的同时，能够有效提高全局搜索能力，避免陷入局部最优。改进算法流程如图3 所示，具体实施步骤为：

（1）使用链接图法构造二维空间环境模型；

（2）采用Dijkstra 算法规划一条从起始点到终止点的初始航迹；

（3）初始化算法参数；

（4）引入Logistic 混沌映射，按照式（4）初始化信息素；

（5）设=0，只蚂蚁放于初始点；

（6）蚁群算法开始搜索，根据式（5）选择下一节点；

（7）判断蚂蚁是否到达终止点，若未到达终止点，跳转至步骤（6），到达终止点则跳转至步骤（8）；

（8）引入模拟退火机制，根据式（6）产生新解并更新最优解；

（9）根据当前航迹规划情况，更新信息素；

（10）=+1，当＞时，输出结果，否则跳转至步骤（5）。

图3 IH-ACO 算法流程图Fig.3 IH-ACO flow diagram

3 仿真分析

为测试IH-ACO 算法在无人机作战中飞行穿越地形障碍、躲避敌方地对空导弹威胁的航迹规划效果，使用MATLAB 2018a 对IH-ACO 算法进行仿真，并与ACO 算法、文献［10］的改进算法（Novel Ant Colony Algorithm，简称NL-ACO）和文献［12］的改进算法（Evolutionary Ant Colony Al⁃gorithm，简称EY-ACO）在相同测试环境下进行对比。构造200 km×200 km 的二维仿真测试区域，进行算法参数初始化：种群数量=20，信息启发因子＝1，期望启发因子＝2，初始条件下信息素浓度＝0.000 09，信息素衰减因子＝0.5，随机概率＝0.6，迭代次数=500，模拟退火初始温度=90 ℃，终止温度=10 ℃，退火系数为0.9，随机产生地形障碍区（不规则多边形表示）和敌方地空导弹威胁区（正方形表示）、起始点Start 和终止点End。

仿真实验1：无人机穿越1 个的地形障碍区，初始点为Start（20，20）、终止点为End（140，90），实验结果如图4 所示。

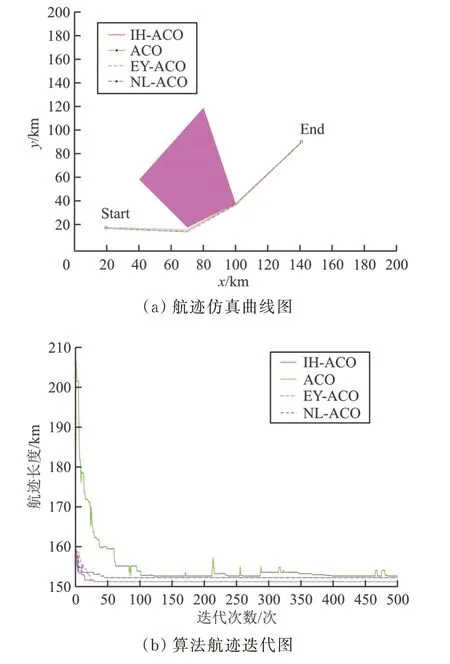
图4 一个地形障碍区时航迹轨迹迭代图Fig.4 Iterative map of track in a terrain obstacle area

仿真实验2：无人机穿越2 个地形障碍区，初始点为Start（20，180）、终止点为End（160，97），实验结果如图5 所示。

图5 两个地形障碍区时航迹轨迹迭代图Fig.5 Iterative map of track in two terrain obstacle areas

仿真实验3：无人机躲避1 个地空导弹威胁区并穿越3 个地形障碍区，初始点为Start（30，100）、终止点为End（180，60），实验结果如图6 所示。

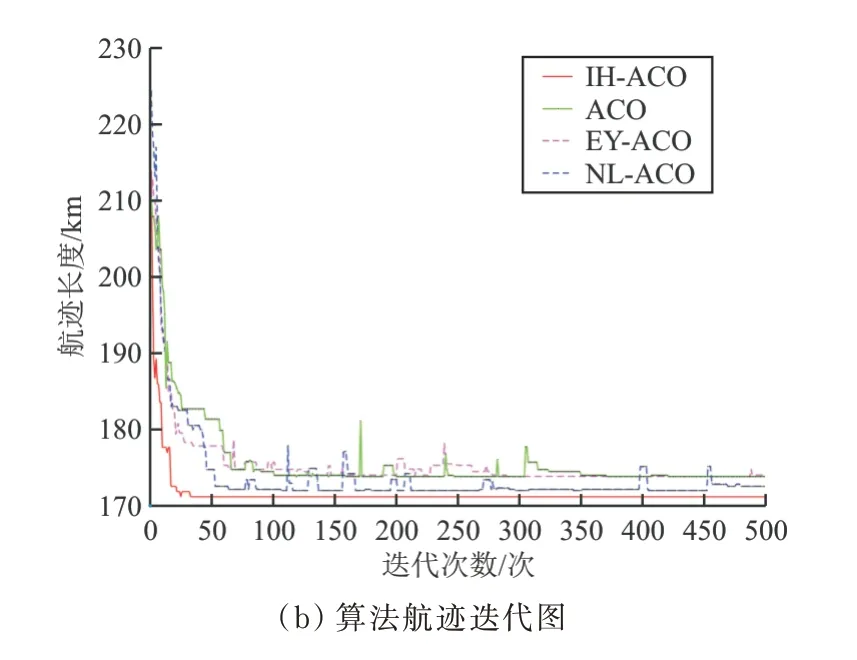
图6 1 个地空导弹威胁区和3 个地形障碍区时航迹轨迹迭代图Fig.6 Iterative map of track trajectory for one surface to air missile threat area and three terrain obstacle areas

仿真实验4：无人机穿越躲避3 个地空导弹威胁区并穿越5 个地形障碍区，初始点为Start（10，100）、终 止 点 为End（180，80），实 验 结 果 如 图7所示。

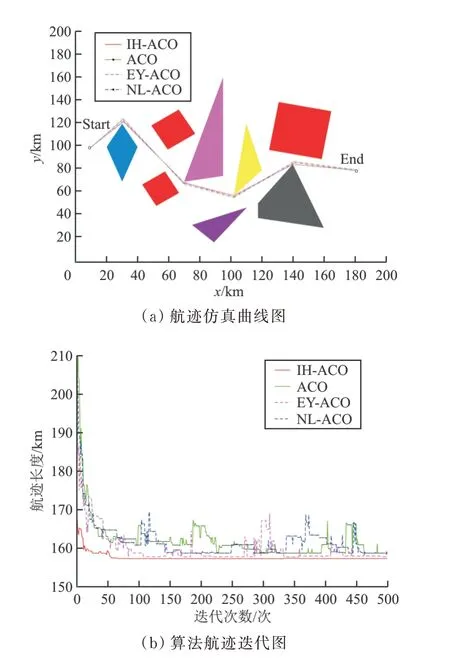
图7 3 个地空导弹威胁区和5 个地形障碍区时航迹轨迹迭代图Fig.7 Iterative map of track trajectory for three surface to air missile threat areas and five terrain obstacle areas

从图4～图7 中的（a）图可以看出：在无人机航迹规划过程中，通过使用ACO 算法、NL-ACO 算法、EY-ACO 算法、IH-ACO 算法，无人机可以有效穿越地形障碍、躲避敌方地对空导弹威胁，证明四种算法都能满足无人机航迹规划的基本要求。

从图4～图7 中的（b）图可以看出：IH-ACO 算法和ACO 算法相比，在迭代次数一定的情况下，IH-ACO 算法搜索得到的最短航迹更小，表明本文改进算法的全局搜索能力得到了增强；IH-ACO算法与NL-ACO 算法、EY-ACO 算法相比，在均可加快收敛速度的情况下，NL-ACO 算法、EYACO 算法在面对复杂环境时出现了停滞在局部最优解的情况，而本文改进算法仍可以很好地进行航迹搜索。综上所述，可以证明IH-ACO 算法可有效解决全局寻优与收敛速度之间矛盾。

四种算法运算结果如表1 所示，可以看出：IHACO 算法在最短航迹、收敛时间上都要优于其他三种算法，表明IH-ACO 算法在精度提高的同时，加快了收敛速度，即IH-ACO 算法具有更好的寻优能力。

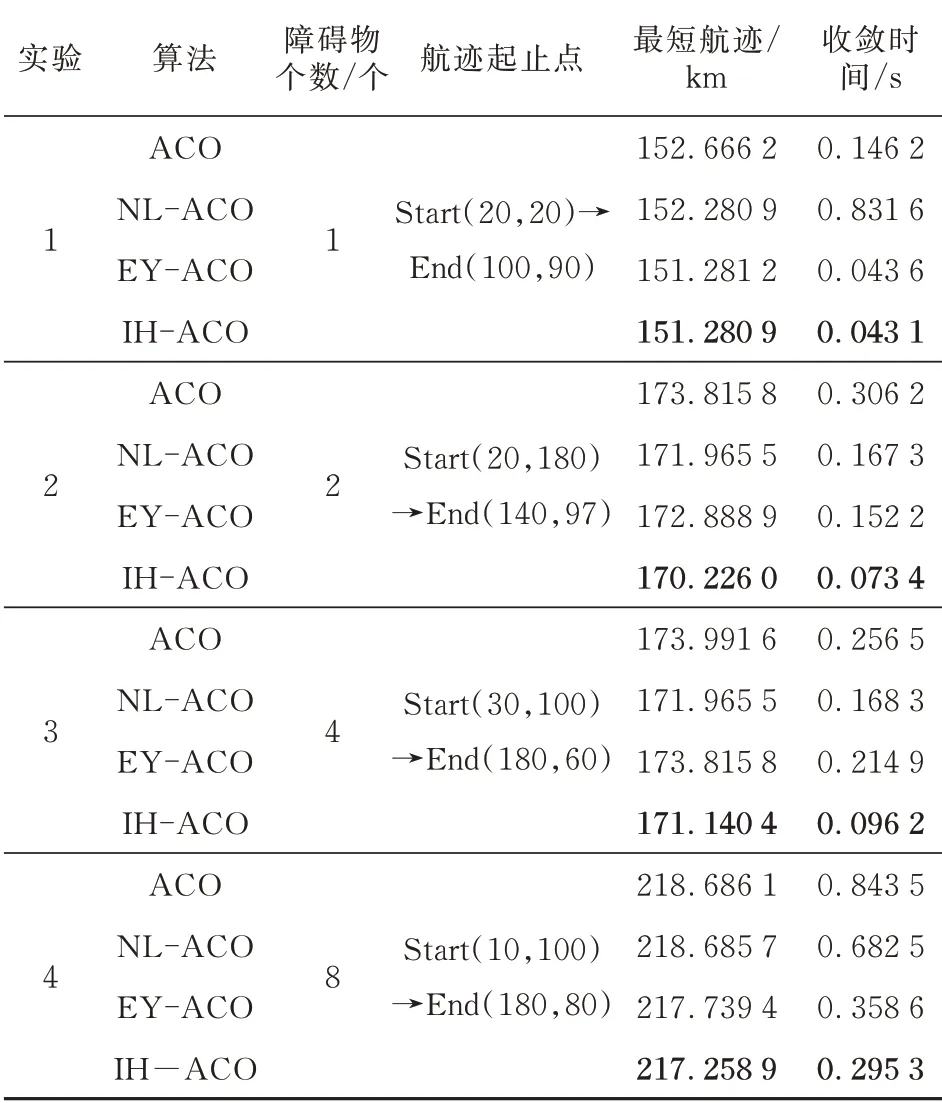
表1 四种算法运算结果Table 1 Calculation results of four algorithms

综上可知，由于在前期进行了Dijkstra 算法初始航迹、Logistic 混沌映射初始化信息素，在中、后期采用多航迹选择策略和模拟退火机制，IH-ACO算法加强了全局搜索能力并提高了算法收敛速度，相比ACO 算法具有更好的航迹规划效果。

4 结 论

（1）使用Dijkstra 算法进行初始化航迹、Logis⁃tic 混沌映射初始化信息素，保证较快的搜索速度，提高蚁群前期搜索能力。

（2）采用多航迹选择策略的状态转移规则，增加解的多样性，有效提高了算法的全局搜索能力。

（3）应用模拟退火机制，避免算法收敛过快陷入局部最优解。

（4）IH-ACO 算法在航迹规划过程中，因Dijk⁃stra 初始化和Logistic 初始化能加快前期搜索效率、多航迹选择策略能增加解的多样性、模拟退火机制能防止早熟收敛，有效解决全局寻优与收敛速度之间的矛盾，在无人机作战的航迹任务规划中有很好的适用性。

（5）HI-ACO 算法与ACO 算法相比，在收敛速度提升的同时保证了全局搜索能力；HI-ACO算法与NL-ACO 算法、EY-ACO 算法相比，在复杂环境中仍能快速、有效地进行航迹搜索，解决了其他改进算法在复杂环境中停滞在局部最优解的问题。

下一步将研究如何将IH-ACO 算法应用到有更多约束条件的复杂环境中进行航迹规划，并结合不同的作战环境和目的要求，提出更实时高效的航迹规划算法。