关于在工程测量中坐标系及相互转换的探讨

刘学

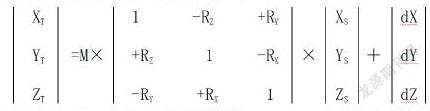
一、地球的三个基本面

地球的自然表面：地球表面是一个高低不平、极其复杂的自然表面，即我们通常所见的山地、平原、江河、湖海等各种地表形态，由于地球内部质量公布不均匀，引起铅垂线的方向产生不规则的变化而成为一个复杂的曲面，测绘工作就是在这样一个复杂的曲面上进行的。

大地水准面：为了处理测量成果和测绘地形图，必须有一个统一的依据面来代替自然表面。设想海水处于静止状态，把它延伸到大陆的内部使之形成一个连绵不断的闭合曲面，这就是大地水准面。它是一个假设的，实际上并不存在，它所包围的形体称为大地体，测绘工作都是以它作为依据的。测量时仪器的“整平”就是使仪器的水平轴平行于过该点的大地水准面，所有的测绘成果都是沿仪器的铅垂方向将地面点首先投影到大地水准面上的。

旋转椭球面：为了制图工作和测量成果的计算的需要，选用一个与大地体相近似的、能用数学方法表达的旋转橢球来代替大地体。旋转椭球是由长、短半径组成的椭圆绕其长轴或短轴旋转而成的，其表面即为旋转椭球面。

各国学者算出的地球椭球长短半径的数值有一定的差异，各个国家根据本国实际进行选用。我们国家在1952年以前采用海福特椭球，从1953年开始改用克拉索夫斯基椭球，现在的1980西安坐标系则采用16IUGG1975（1975年第16届国际大地测量与地球物理联合会）的椭球推荐值。

二、大地坐标系的概念

坐标系是一个最基本的问题，但在测绘工作中时时刻刻要和它打交道。

为了在地球椭球面上确定点位，必须先将椭球与大地体间的相对位置确定下来，这个过程称为地球椭球的定位。

建立一个大地坐标系的三要素如下：

1、确定某一椭球的形状和大小;

2、定位与定向：即确定该椭球中心的位置及确定以该椭球中心为原点的空间直角坐标系坐标轴的指向;

3、确立大地原点。

椭球的形状和大小、椭球的定位和定向与大地原点上大地起算数据的确定是相互关联着的。对于经典的参心大地坐标系的建立而言，参考椭球的定位和定向是通过确定大地原点的大地起算数据来实现的，大地原点大地起算数据确定后，参心大地坐标系即告建立;而大地原点大地起算数据的确定是参考椭球定位和定向的必然结果.

世界各国差不多都有自己的坐标系。我国除北京54坐标系和西安80坐标系外，在全国统一坐标系之前还存在若干地方坐标系，由于原点的位置和定位精度及椭球大小等方面的差别，地面上的同一点在不同的坐标系中会有不同的经纬度坐标。

三、大地坐标系的类型

1、地心坐标系：

以地球的质心为坐标原点建立的空间直角坐标系，一般以空间大地直角坐标X、Y、Z描述点位。X轴在赤道面上穿过本初子午线，Y轴在赤道面上穿过东经90°线，Z轴指向某一平极点。如WGS-84即属此类型坐标系。

2、参心坐标系：

该类坐标系最显著的特点是它与参考椭球的几何中心有着紧密的联系。它可以细分为参心空间大地直角坐标系和参心大地坐标系两种。“参心”两字意思在指参考椭球的几何中心，选一个参考点作为测量的起算点（大地原点），在我们国家曾出现过参心大地坐标系主要有BJZ54（原）、GDZ80和BJZ54（新）三种。

四、几种常用的坐标系

1、WGS—84世界大地坐标系

该坐标系是一个协议地球坐标系，坐标原点为地球的质心，其地心空间直角坐标系的Z轴指向BIH（BIH--国际时间局）1984.0定义的协议地球极（CTP）方向，X轴指向BIH1984.0的零子午面和CTP赤道的交点，Y轴和X轴、Z轴垂直构成右手坐标系，别名为1984年世界大地坐标系统系。

2、1954年北京坐标系

该坐标系是我国解放后第一个参心坐标系，所提供的点的坐标是局部平差的成果，使得我国天文大地网的整体精度主要取决结构单薄的一等三角锁，而结构坚强精度高的二等全面网的精度得不到充分发挥，在使用过程中将逐步被淘汰。

3、1980西安坐标系

又称简称西安大地原点，是利用我国30年来天文、重力、三角测量资料，根据建立参心大地坐标系的原理得出的，在该坐标系中所提供的是全国天文大地网整体平差的成果。

4、1954年北京坐标系（整体平差转换值）

它是由1980西安坐标系派生出来的一种坐标系。二者的差别在于：对于空间直角坐标系来说，仅仅相差三个平移量;对于大地坐标系来说，还包含有椭球元素的不同。虽然它们的大地起算点相同，但起算数据不同。据计算，两者的大地经度相差-2.91″，大地纬度相差0.39″。显然也是整体平差的结果。

五、坐标系间的转换

1、坐标转换的一般过程

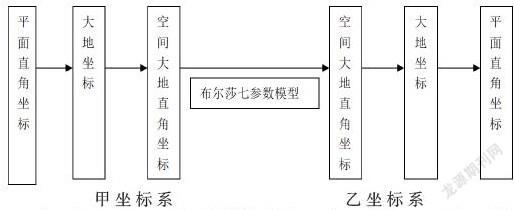
现在假设要把甲坐标系的平面直角坐标转换成乙坐标系的平面直角坐标，其转换过程如下图所示：

2、同一个椭球的坐标变换

平面直角坐标与大地坐标之间的变换就是一个坐标正反算问题，在这里不再赘述。

大地坐标换算为空间大地直角坐标的公式如下：

X=（N+H）cosBcosL

Y=（N+H）cosBsinL

Z=[（1-e2）N+H]sinB

式中N为纬度B处的卯酉圈曲率半径，H为大地高，B为大地纬度，L为大地经度，e为第一偏心率。

应当指出，H应为点相对椭球面的高度。但经典大地测量得到的通常是与重力相关的高度值，也就是相对国家高程基准的高度，绝大部分情况下二者有一定的差值，所以经过坐标系转换后，同一点的海拔高程会有一定的差异（实际上海拔高程不需要转换，故不必理会），但一般不会导致平面坐标值产生太大的影响。

反之，空间大地直角坐标也可以转换为大地坐标，可以采用直接解法也可用迭代法，其中一个迭代法公式如下：

B=tg -1[（Z+e2NsinB）/（x2+Y2）0.5]

L=tg -1（Y/X）

H=XsecLsecB-N

3、不同椭球的空间大地直角坐标系的转换

不同椭球所对应的空间直角坐标系是不同的，不同的两个空间大地直角坐标系可以通过平移和旋转取得一致，转换方法有很多种，其中最著名的是布尔莎七参数变换公式，它有三个平移参数、三个旋转参数和一个尺度变化系数，其公式如下：

式中dX、dY、dZ为三个平移参数，RX、RY、RZ为三个旋转参数，M为尺度系数。

七参数坐标变换公式除布尔莎公式外，还有莫洛琴斯基公式和范士公式。这三种公式，它们间的七个参数相差较大，在各自构成完整的数学模型中，参数间存在着明显的解析关系，可以相互进行转换。分别用它们来换算点的坐标时，其结果完全相同，因此，这三种公式是等价的，当RX=RY=R=M=0时，上式即变为三参数公式。三参数公式表明两个空间直角坐标系尺度一致，且各坐标轴互相平行。如果区域范围不大，最远点的距离不大于30㎞（经验值），可选用三参数法转换。同理，略去某些参数，可分别得四参数、五参数、六参数等坐标变换公式。公式中的七个变换参数，一般利用公共点（一个区域需要三个以上）的两套空间直角坐标系的坐标值，用最小二乘法解得。

必须注意的是，如果有两种不同空间直角坐标系变换时，坐标变换的精度取决于坐标转换的数学模型和求解变换参数的公共点坐标精度外，还与公共点的分布有关。鉴于地面控制网系统误差在不同区域并非一个常数，且在不同区域也不一样，所以采用分区进行坐标转换计算变换参数，这样才能更好的反映实际情况以便提高坐标变换精度。

六、结束语

从上面的讨论可知：地面上同一点，在不同的大地坐标系中的大地坐标即经纬度值是有一定差异的;不同的大地坐标系所采用的参考椭球亦不同，它们之间的变换方法是采用一定数量的公共点用七参数法进行变换;参心坐标系中的高程值不用变换，仍采用有关高程基准的高程;分区进行坐标转换计算变换参数才能更好的反映实际情况以便提高坐标变换精度。

坐标系转换问题在测绘工作中会经常遇到，可能有部分同志对此比较陌生或是认识比较模糊，本文的重点在于弄清坐标系的概念，理清坐标系转换的思路，分清坐标系转换的过程，以便在工作中概念明确、条理分明，不致出错，希望本文对实际转换操作能有所帮助。致于具体的转换方法或计算程序，在许多成熟的专业软件如MAPGIS、南方CASS等软件中都集成了此功能，还有不少这方面的优秀专业软件，本人也不具备软件编程的能力所以就不在此浪费时间，何况有那么多好东西可用，且不快哉！

参考文献：

[1]武汉测绘学院 祝国瑞、尹贡白编著 《普通地图编制》测绘出版社 1985年

[2]青島海洋研究所 戴勤奋译 《坐标系转换公式》

[3]朱华统，杨元喜，吕志平编著 《GPS坐标系统的变换》测绘出版社 1994年

[4]刘山洪，邓彩群《坐标转换与坐标变换研究》吉林建筑大学学报2016年01期

[5]朱华统.常用大地坐标系及其变换[M]. 北京：解放军出版社，2003.

[6]CJJ/T8-2011 《城市测量规范》住房和城乡建设部

[7]GB 55026-2020《工程测量规范》住房和城乡建设部