基于改进Canny 算子的图像边缘检测算法

李一波 刘佰仑

（沈阳航空航天大学，辽宁 沈阳 110136）

1 概述

如今，在众多领域都会应用到图像识别技术，而在计算机对图像感兴趣的区域进行提取时，边缘信息是非常重要的。传统边缘检测算子有Sobel、Prewitt、Roberts、Laplacian、LOG 等，它们都是图像局部区域窗口的梯度算子，在进行检测时非常容易受到噪声的影响。针对Canny 算法存在的问题，许多研究者做出了相应的改进。有人提出自适应中值滤波不仅可以有效地减少噪声对数据的影响，还可以较好的保留图像基本的边缘信息。使用了一种新型滤波器与均值滤波器混合使用的滤波方法代替了原来的高斯滤波器，该算法能够去除大量椒盐噪声，同时也能保留图像的边缘细节，但两种滤波器混合使用会使图像产生失真现象。采用中值滤波器与高斯滤波器混合的方法进行滤波操作，改进后的Canny 算法图像边缘信息连续性更强,单边缘响应效果较好,边缘检测效果更优,但算法的执行效率还有待进一步提高。

2 传统Canny 边缘检测算法

传统的Canny 边缘检测算法最初由John F. Canny 提出，并设定了信噪比准则、定位精度准则、单一边缘响应准则来提高边缘检测精度。为满足这3 条准则，John F. Canny 在一阶微分算子的基础上，增加了2 项改进，即非极大值抑制和双阈值。多边缘响应、边缘的定位精度利用非极大值抑制来控制；双阈值能减少边缘的漏检率。其检测流程如图1 所示。

2.1 使用二维高斯函数与目标图像进行卷积运算以得到平滑后的图像，二维高斯函数G（x，y）为：

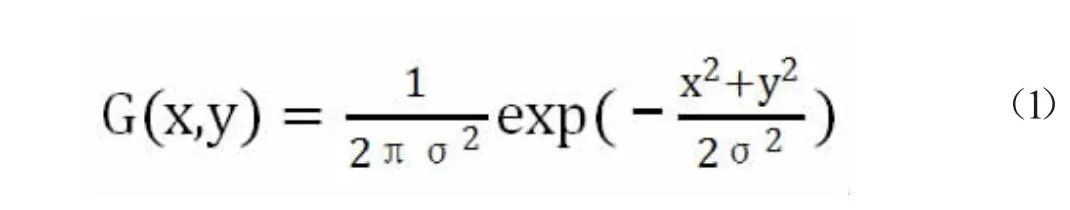
高斯函数与目标图像的卷积公式为：

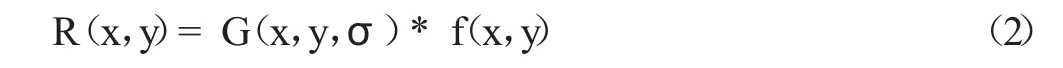
式中：σ 为高斯函数的标准差，其大小的变化可以改变图像的平滑程度，R（x，y）为高斯函数与输入图像进行卷积运算之后的图像；f（x，y）为输入图像；“*”代表卷积运算。将高斯函数转化为高斯滤波模板，可以提高运算效率。

2.2 计算梯度幅值和方向，利用Sobel 梯度模板分别计算图像在像素点（x，y）处x 和y 方向上的偏导数。

其在x 方向上的偏导数Ⅰx为:

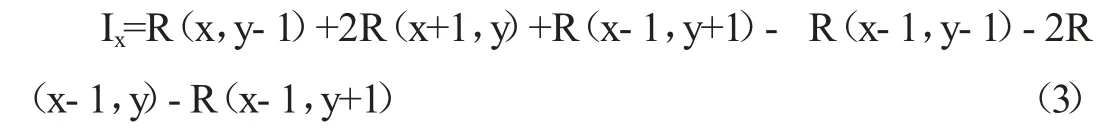
在y 方向上的偏导数Ⅰy为:

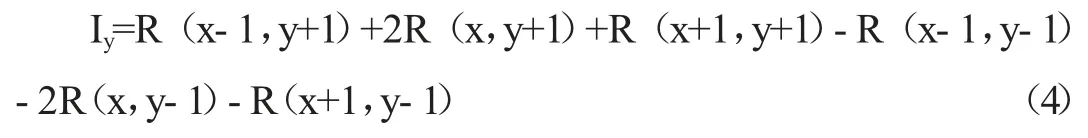
式中：R（x，y）为像素点（x，y）处的像素值。

利用二范数计算其梯度幅值O 所得:

其梯度方向为：

3 改进的Canny 边缘检测算法

原始的Canny 算法在对图像进行预处理的时候只能对其进行平滑处理，对受到噪声污染的图像并不能对其进行滤除，故本文设计了一种能够将椒盐噪声滤除的新型滤波器。并且计算了四个方向的梯度幅值，在进行双阈值连接时采用最大间类方差法来确定最优阈值而非人工确定，可以提取到更加完整准确的边缘信息，并且有更好的自适应性。

3.1 新型滤波器设计原理

3.1.1 噪声点与边缘点的区分

图片中的椒盐噪声非常明显，其特征是该点的像素值与邻域八个点的像素值差距过大，故可以根据像素值变化幅度的大小来判断该点是否为像素点。而判断其变化幅度大小的方法就是看其导数的大小。当导数越大时则说明其像素值变化的幅度越大。因为图像的边缘信息点也存在与周围点像素值差距过大的情况，故需要进一步进行判断。

一幅灰度图像像素点的像素值为0-255，所以本文将像素值为0 或者255 的点可以定义为噪声点。所以新型滤波器的滤波窗口可以定义为图片中像素值为0 或255 的点，之后计算该点与邻域中其他点的方向导数f（q，r），其公式为：

3.1.2 算法流程描述

3.1.2.1 设置一个3×3 的滤波窗口，设定一个阈值T，并令窗口开始移动。

3.1.2.2 窗口中心不为0 或255，窗口继续移动，否则转至3.1.2.3。

3.1.2.3 计算该中心像素点的像素值F(x，y)，领域内8 个方向的导数f(q，r) 。如果|max［f(q，r)］|＜T，窗口继续移动。如果|min［f(q，r)］|＞T，转至步骤3.1.2.4。如果以上皆不成立则转至步骤3.1.2.5。

3.1.2.4 以F(x，y) 为窗口中心，利用窗口中的中值替代F(x，y)。

3.1.2.5 将窗口中心移动至f(q，r)＜T 的点。定义此点的像素值为F (i，j) 以此点为中心重新计算邻域内8 个方向导数。若集合f(q，r)中有超过3 个小于阈值T。则该点为边缘点。否则转至步骤3.1.2.4。

3.1.2.6 窗口移动至最后，算法结束。

3.2 改进的梯度幅值计算方法

原始的Canny 算子在计算图像梯度幅值时采用2×2 领域一阶有限差分运算，只考虑到水平和垂直方向上的梯度值，因此易受到来自外界噪声的干扰，故本文在Soble 算子的基础之上加入45°和135°方向来计算梯度幅值。在3×3领域内4 个方向上的梯度模板见式（8）：

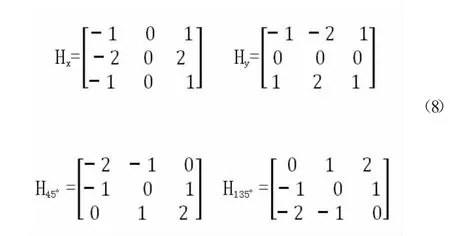
将水平方向、垂直方向、45°方向、135°方向的梯度模板分别与滤波后的图像进行卷积运算，得到4 个方向上的梯度分量Mx、My、M45°、M135°，最后求得梯度幅值M，见式（9）：

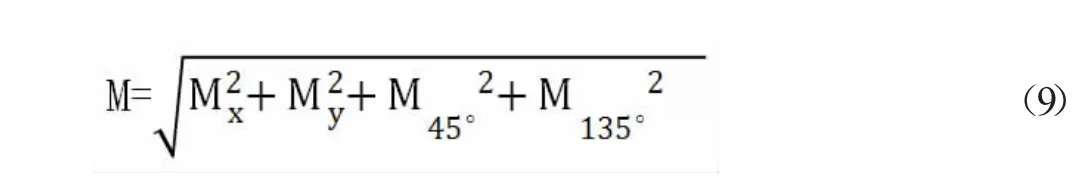
4 个方向上的梯度分量合成到水平和垂直2 个方向上总的梯度分别为Mx、My，分别见式（10）、式（11）：

由Mx、My求得梯度方向δ，见式（12）：

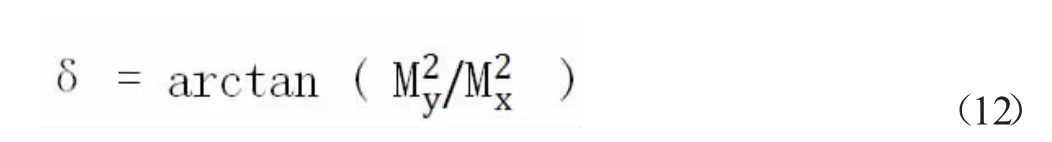
3.3 Otsu 算法求高低阈值

原始的Canny 算法是由人工来设定高低阈值来进行高低阈值的连接，而使用最大间类方差法可以自适应确定最优阈值，增加算法的自适应性，是边缘更加完整，准确。

在含有L 个不同灰度等级的M×N 图像中，每个灰度值对应的像素值为ni，i∈[0,L-1]，则其中某一像素i 所出现的概率为Pi，见式（13）：

假设选择1 个阈值k,k∈[0,L-1], 将图像像素灰度分成2 类，即前景W0和背景W1,二者灰度等级范围分别为：W0∈[0,k]，W1∈[k+1,L-1]。因此，某一像素落在W0、W1上的概率分别为Pw0（k）、Pw1（k），分别见式（14）式（15）：

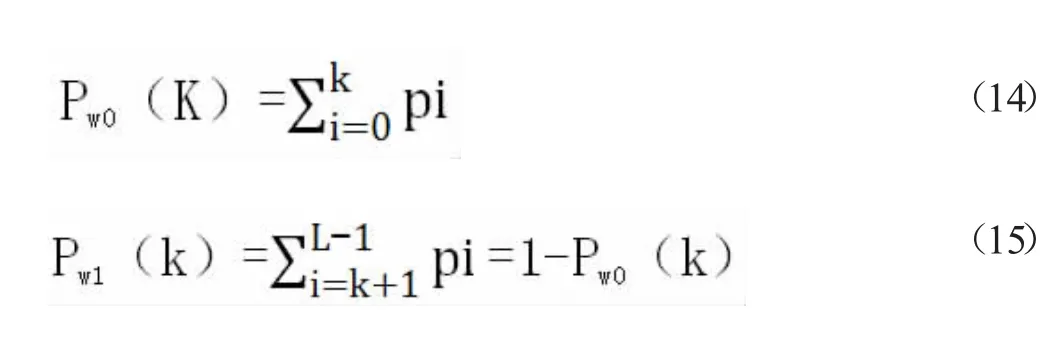
前景W0和背景W1的平均灰度值分别为h0（k）和h1（k），分别见式（16）和式（17）：

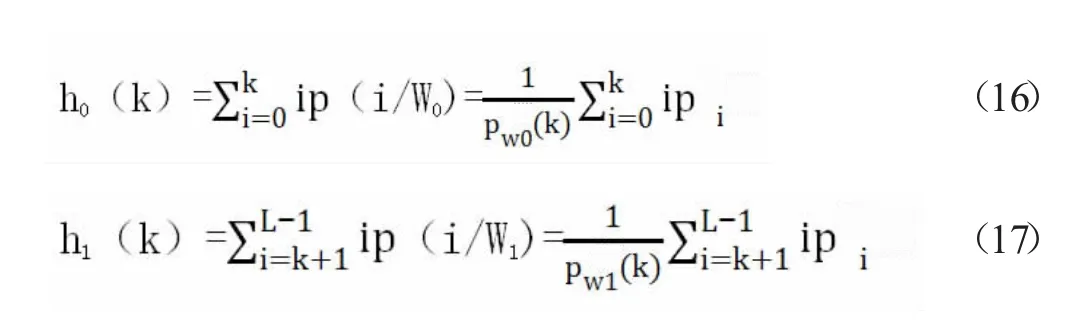
则整个图像的平均灰度值为h（k），见（18）：

由上述公式可求得前景W0和背景W1间的最大间类方差δ2，见式（19）：

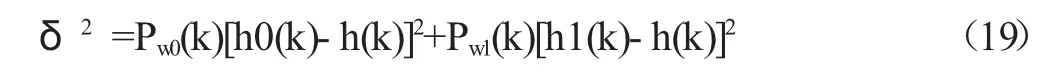
在不同的k 值下求间类方差，当间类方差δ2取得最大值时所对应的k 值就是所求得的最优阈值，将此最优阈值设为高阈值Th，低阈值为Th/2。

4 实验结果及分析

一个算法的有效性与合理性必然是通过实验来证明的，为了验证本文提出的算法的效果，本文使用matlab2016a 对一幅lena 图片和一幅篮球鞋图片进行边缘检测，并将本文的算法与原始的Canny 算法进行了比较。

实验结果如图2 所示。两幅图片中都添加了密度为0.02的椒盐噪声。从对比结果中可以看出原始的Canny 算法会将椒盐噪声判定为边缘点，从而导致误检，且检测到的边缘点存在断层的问题。而本文的算法可以很好的滤除椒盐噪声，边缘检测能力不受影响，并且使提取到的边缘更加完整，能够检测出图像的弱边缘。

图2 边缘检测结果对比

为了展示算法的检测性能，本文使用了五个指标进行评判，即MSE（均方误差），SNR（信噪比），TPR（边缘点检测的准确率），TNR（背景点检测的准确率）和ACC（边缘检测的整体精度），其定义如下:

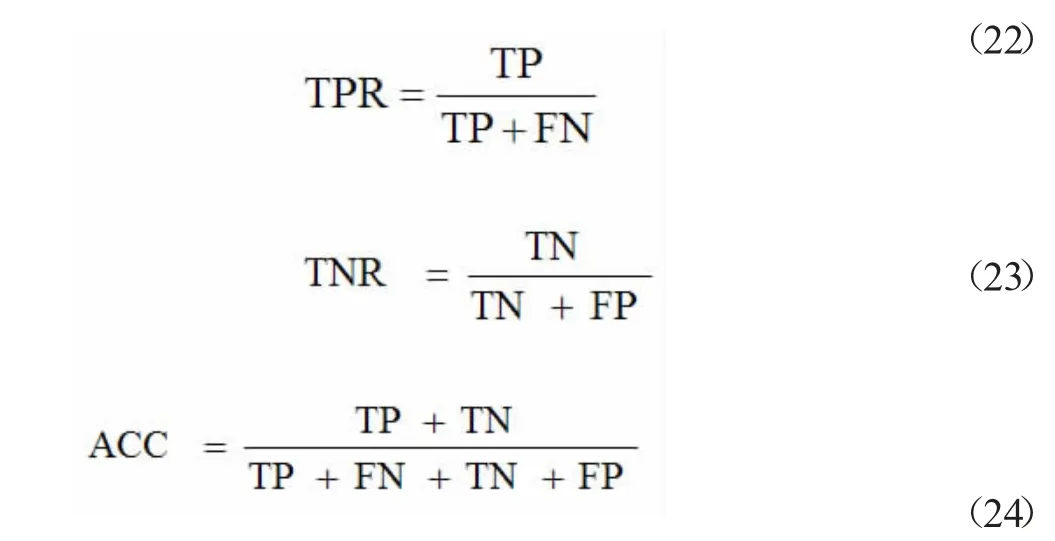
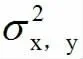
本文将多幅图像进行实验，分别求取了以上五种指标并取其平均值，将原始的Canny 算法与本文算法进行对比，统计结果如表1 所示。由表可知，本文算法的五个性能指标都优于前三种算法，即具有较高的边缘点检测的准确率和精度。

表1 示边缘检测性能指标对比

结束语

为了让边缘检测的正确率与功能性更好，在原始的Canny 算法上进行了改进，以一种新型滤波器代替了高斯滤波器，在计算梯度幅值时增加了两个方向来达到去噪的目的，最后采用最大间类方差法来自适应确定最优阈值使检测到的结果更完整，准确。