配电网小电流单相接地故障选线方法研究
豆文政, 冯杰, 孟春旅, 温宗仁, 吉训周
(海南电网有限责任公司,乐东供电局,海南,乐东 572500)
0 引言
配电网作为用户和输电网的重要纽带,直接面向用户,与人民的生活密切相关,是国民经济和民生的重要基础设施[1]。我国35 kV以下的配电网系统也被称为小电流接地系统,单相接地故障发生时,如果不及时处理的话,对配电网的正常运行会产生很多影响,从而发生严重的安全事故[2]。因此,要求电网工作人员及时、准确地发现故障,并根据需要排除故障[3]。在配电线路故障类型中,单相接地故障占所有故障类型的65%以上。因此,对小电流接地故障选线方法的研究对电网安全具有重要的意义。由于小电流接地故障电流很小,随着非线性负载的增加,故障电流信号中包括大量的谐波成分[4]。若不处理故障信号,则故障线路的选择有可能存在非常大的误差,保护装置有可能误动作,故障路线选择的准确性由故障信号处理质量决定。文中将双树复小波应用于配电网小电流故障选线,结合能量相对熵作为故障选线判据。小电流信号在通过双树复小波变换处理后,使用能量相对熵来确定故障线路,最后通过仿真,验证该方案的有效性。
1 系统概述
小电流接地系统可以分为3类:中性点不接地、经消弧线圈接地、经高阻接地[5]。这3种接地方式特性不同,在实际应用中存在差异,文中采用中性点经消弧线圈接地。
消弧线圈通常由电感和电阻串联或并联,通常仅适用于大电容电流系统。原理是消弧线圈所提供的感应电流抵消容性故障电流[6]。随着配电网越来越复杂。如果发生单相接地故障,故障电流可能超过阈值,无法自动控制灭弧。因此,有可能威胁到配电网设备的绝缘和安全。为了避免这样的故障,如图1所示,必须在系统的中间点安装消弧线圈装置。
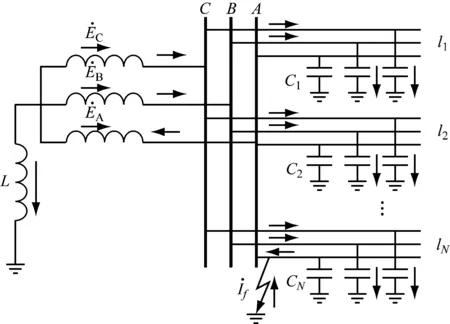
图1 单相接地故障(中性点经消弧线圈接地)
(1)
补偿度P定义如式(2),
(2)
当P=0时,称为“全补偿”;当P<0时,则称为欠补偿;当P>0时,它被称为“过补偿”。这3种补偿各有优点和缺点[7]。当采用全补偿时,往往会产生谐波过电压,欠补偿可以避免这一现象。但如果从系统中移除组件,欠补偿将转变为全补偿。过补偿被广泛使用,通常为8%或10%。
2 双树复小波变换分析方法
2.1 小波分析方法
小波分析是故障选线的理想选择,具有较强的识别能力和自适应能力,但其抗干扰能力差。在信号处理中,有用的信息不能完全提取出来,对后续分析很不利[8]。双树复小波变换(DTCWT)具有小波变换(DWT)的优点,而且还克服了许多DWT的不足[9]。当处理平移信号时,DTCWT保持原始信号的信息。在信号重建期间避免频率混叠,对随后的信号处理更有利。
DTCWT是二叉树(树a和树b)的结构。树a对应于实部,树b对应于虚部。在信号分解和重构期间,由于滤波器树a和b之间的延迟保持在一个采样间隔内,所以DTCWT可以成功地用于双树小波分解系数。两棵树信息可以互补。DTCWT可以有效地使用每个系数二分法来分解每一层,这有利于加快计算速度[10]。DTCWT的3层分解重构图由图2给出。
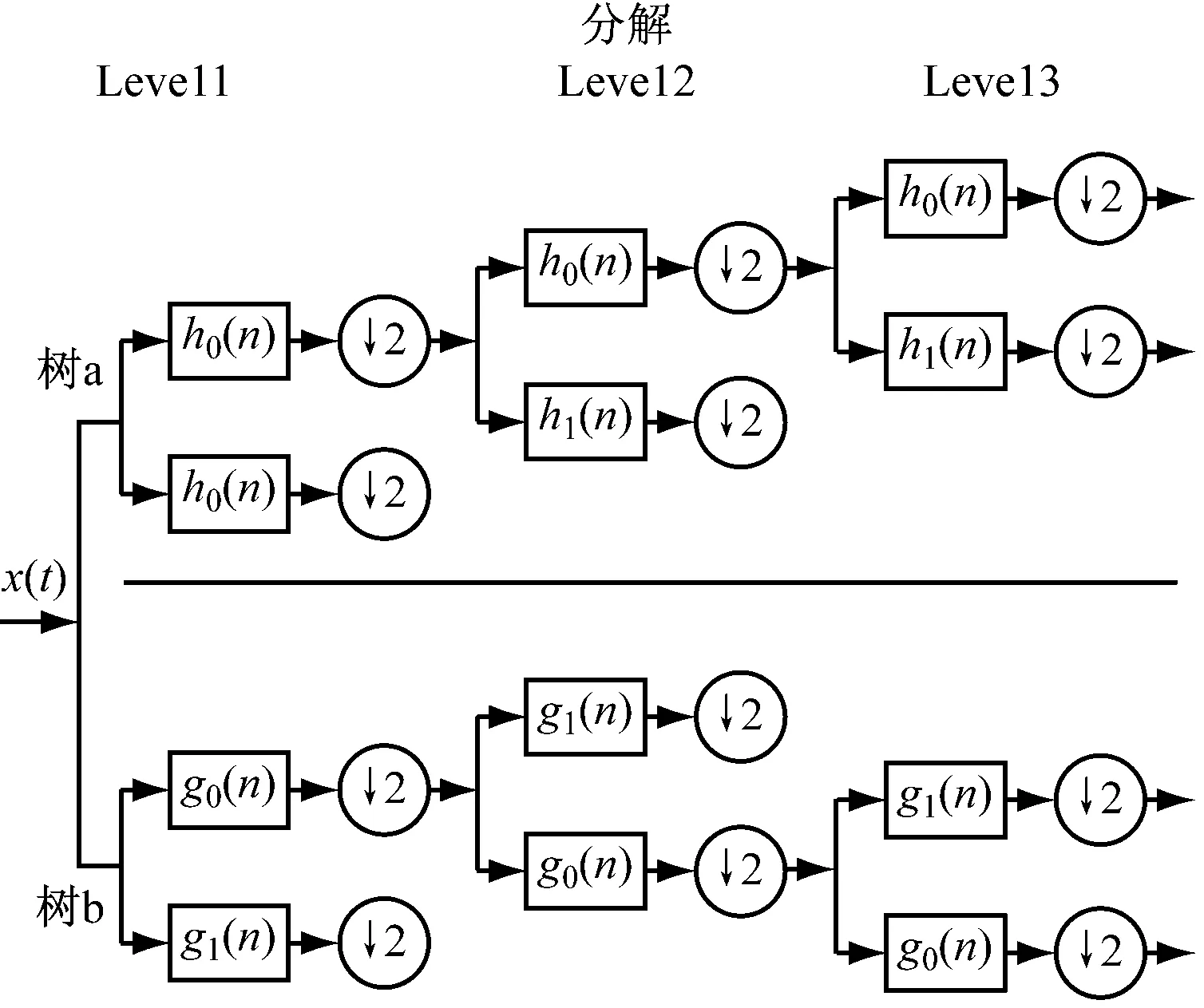
(a)分解过程
根据DTCWT构造方法,小波可以表示如下,
φ(t}=φh(t}+iφg(t}
(3)
式中,φh(t}、φg(t}表示2个实小波,i表示复数单位。
对实数部分的小波变换,利用式(4)和式(5)可以得到小波系数和尺度系数,其中j=1,2,…,J,
(4)
(5)
对于虚数部分的小波变换,通过式(6)和式(7)可以得到小波系数和尺度系数,
(6)
(7)
再由式(8)和式(9)可以得到最小波长和尺度系数,
(8)
(9)
DTCWT之后的重构信号如式(10),
x(t}=dj(t}+cj(t}
(10)
导出原始信号x(t)的重建信号如式(11),
(11)
式中,TRe表示小波分解树a的系数,Tlm表示小波分解树b的系数。
2.2 选线依据
小电流接地系统发生单相接地故障时,零序电流的幅值和能量均大于正常电路。然而,由于系统对信号的干扰,与正常电路相比,故障线路的能量差有时较小,很难区分能量差。能量相对熵(Energy Relative Entropy,ERE)可以放大这种差异使微小差异容易区分。ERE改善故障的能量分布特性,显示信号的差异,根据ERE的大小选择故障线路。
用软件模拟了系统的单相故障,得到各零序电流。由于信号中含有噪声,这对原始信号影响很大,不利于选线。因此,需要消除噪声,通过DTCWT分解重构,通过重构信号系数计算小波能量,得到综合小波能量的相对熵。
选择最大的3个排序Hp、Hq、Hr,如果Hp>Hq+Hr,则相应的线是故障线;否则,母线故障。具体步骤如下。
步骤一:确定母线的零序电流是否达到设定值,达到则启动设备;在故障之前和故障之后的一个工频周期中记录每条线路的零序电流。
步骤二:使用DTCWT分解重构信号,并通过变换小波系数获得尺度j下复小波的能量。
步骤三:计算每个电路综合小波能量的相对熵。
步骤四:根据Hp>Hq+Hr选择线路,选择线路流程图如图3所示。
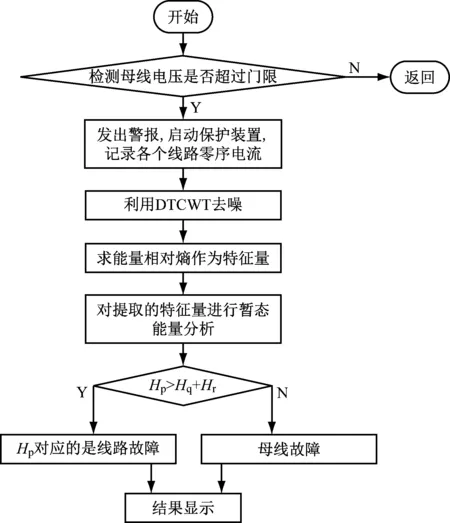
图3 故障选线流程图
3 仿真结果与分析
3.1 仿真模型建立
通过MATLAB/Similink工具的Simpoer Systems对系统进行仿真,构建110 kV /10 kV电压下的模拟电网。仿真模型如图4所示。
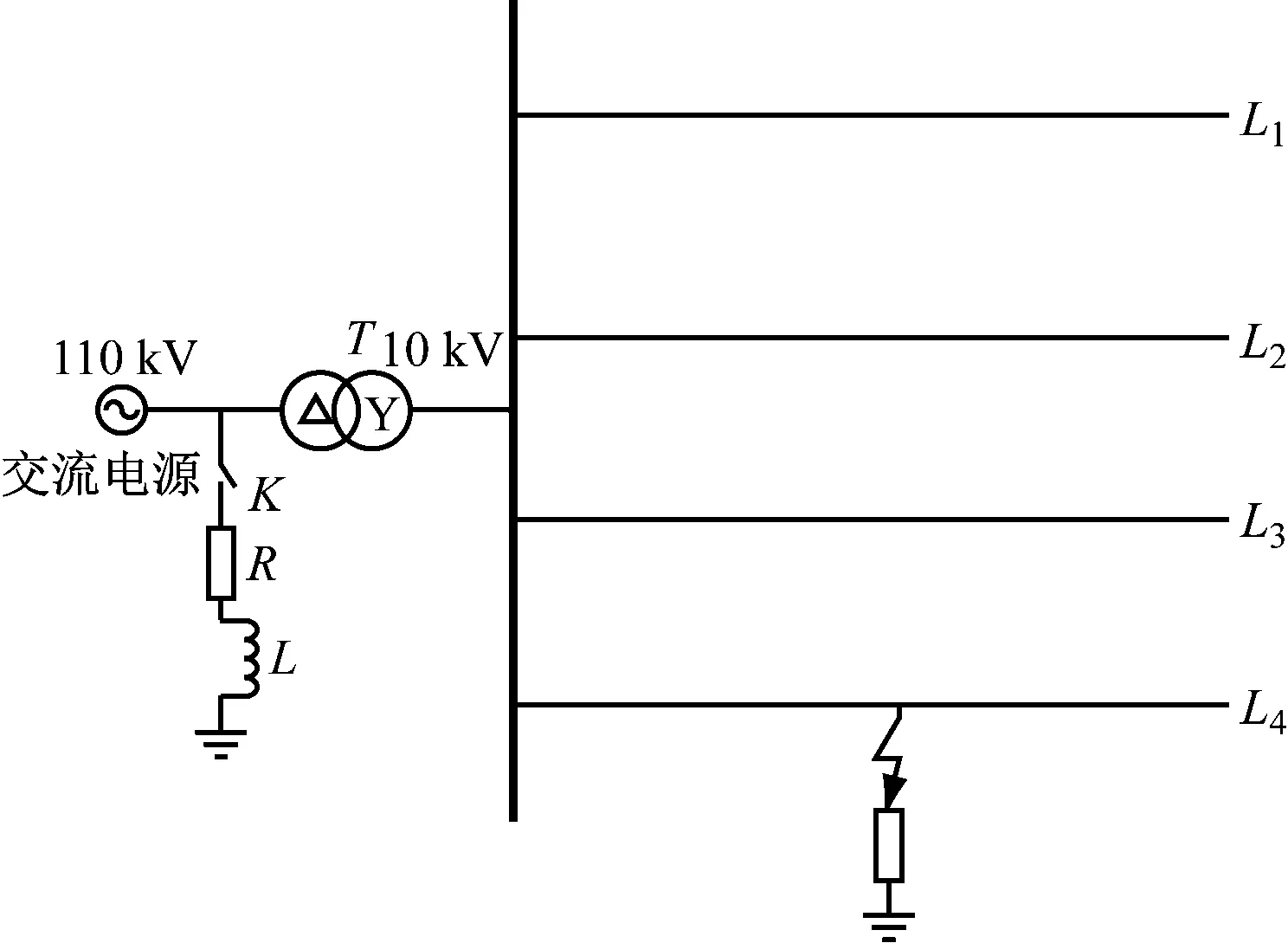
图4 系统模型
图4中,中性点经消弧线圈接地。从L1到L4的长度分别为10 km、15 km、25 km和35 km。采样频率为10 kHz,灭弧线圈采用过补偿,补偿度为8%。
线路的正序参数:R1=0.17 Ω/km,L1=1.20 mH/km,C1=9.1 nF/km。
线路的零序参数:R0=0.23 Ω/km,L0=5.49 mH/km,C0=6.0 nF/km。
3.2 仿真结果分析
小电流接地系统非常复杂,数据终端不断采集数据。然而,通过波形来选择线路是非常困难的,不可能一直观察。采集的数据量也很大,导致人力资源的浪费。利用数字方法记录数据,通过算法选择故障线,方便快捷,是本文研究的基本方向。下面是MATLAB/Simulink仿真实例,用于验证该方法的有效性。故障在L4线距离母线8公里处。在A相接地故障发生时,故障发生在0.01 s,过渡电阻25 Ω。各电路故障后的零序电流波形如图5所示。
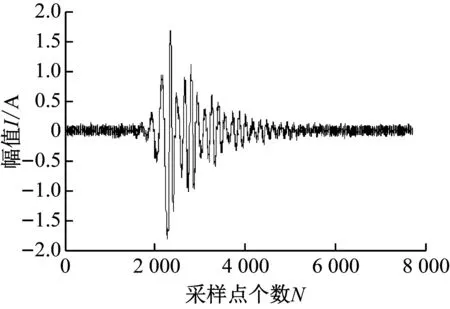
(a)电流波形(L1零序)
根据图5中各电路的零序电流图和上述理论可知,与正常线路非常相似,但是故障电路差别很大,幅度大,相位与正常电路相反。另外,由于信号受强噪声的影响,必须去除信号中的噪声。由于正常线路之间的相似性,只比较了L1和L4的零序电流。
如图6所示,DTCWT处理的信号很好的保留了原始信号特征。但是DWT处理信号缺乏边缘信号,会丢失一部分原始信号,因此,DTCWT在分析和处理原始信号方面具有明显的优势,准确性更高。

(a)故障信号
通过推导得到各线路综合小波的能量相对熵分别为2.085 2,0.927 7,6.790 9和33.768 9。取前3个最大值,Hp=33.768 9,Hq=6.790 9,Hr=2.085 2。因为Hp>Hq+Hr,根据上述选择原则,可以确定L4为故障线。各线路小波能量的相对熵见图7。
由图7可知,每条线路小波能量的相对熵可以清晰地看到。与波形相比,该方法简单直观,消除了许多问题。为了验证该方法的适应性,仿真了不同条件下的算例,结果如表1所示。
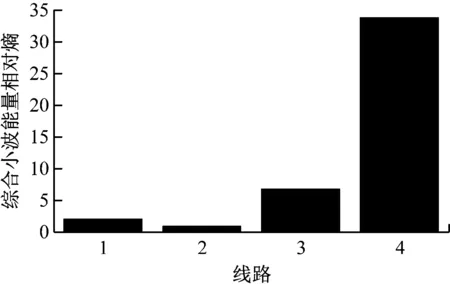
图7 各线路综合小波能量相对熵
由表1可知,在某一线路故障时,其相对熵远大于其它线路能量相对熵,验证了该方法的有效性。
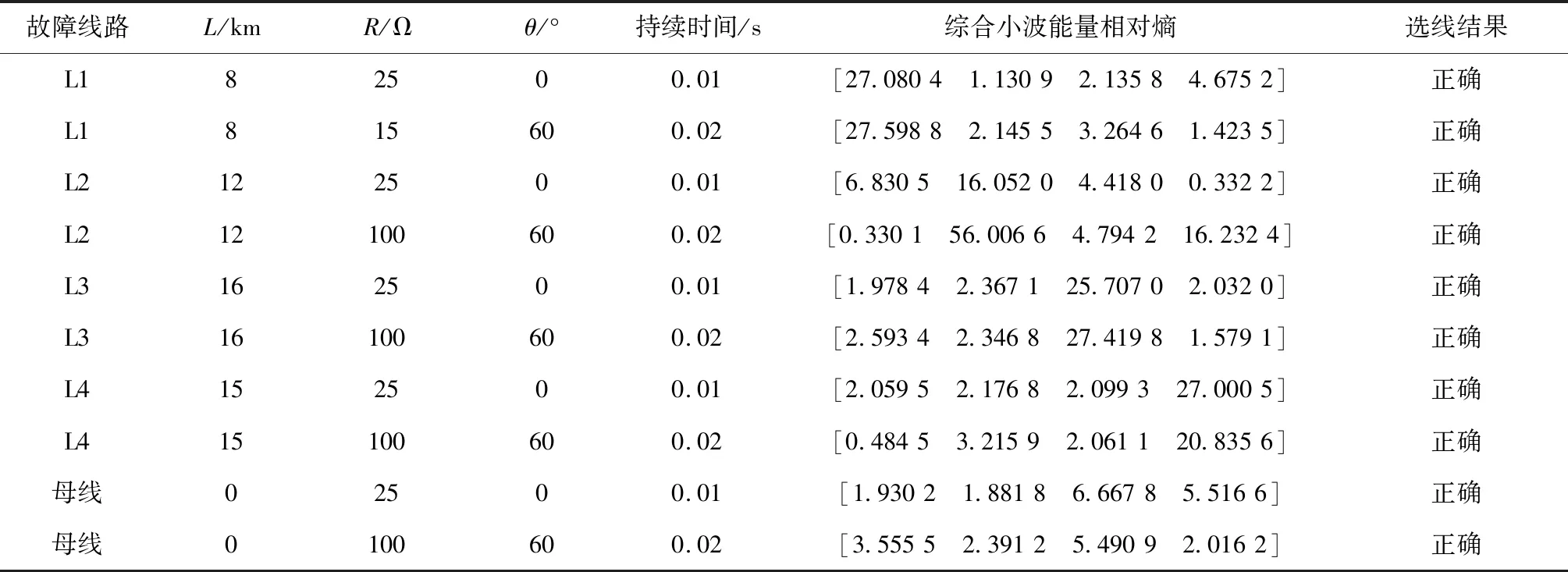
表1 各工况下故障选线结果
4 总结
文中在分析了小电流接地系统的特征之后,在小电流接地系统故障的选线中应用双复小波变换,把能量的相对熵作为故障选线的依据。仿真验证了该方法的有效性,而且表明,此方法不受接地电阻、故障时间、故障相位等因素的影响。在不同的工作条件下,可以快速准确地选择故障线路。根据实验室现有设备和数据规模,系统故障选线仍处于初级阶段。在此基础上,逐步完善和改进将成为下一步工作的重点。

