基于灰狼算法优化DBN的医院网络异常流量识别

黄波， 杨正， 王超

(1.广州市第八人民医院，广东,广州 510060;2.福建师范大学,光电与信息科技学院,福建,福州 350007)

0 引言

随着现代信息技术和移动互联网技术的飞跃式发展，各行各业的信息化和网络化进程不断加快。为了有效提升工作效率，缓解人力不足的压力，政府、企业、医院等纷纷开始利用互联网技术进行管理改革。医院管理系统中管理着海量患者隐私信息和技术资料，如果遭受网络攻击，将会对医院带来巨大经济损失，对社会造成不良影响。所以开展医院网络异常流量的识别研究是非常重要的[1]。现有网络异常流量识别主要有神经网络、支持向量机、深度学习等[2-4]。为更好地提升医院的网络异常流量识别的准确度和识别效率，本文尝试将灰狼优化算法(Grey Wolf Optimization，GWO)和深度置信网络(Deep Belief Network，DBN)结合起来，提出一种基于GWO-DBN的医院网络异常流量识别方法。

1 灰狼优化算法

在标准GWO算法[5]中，用α、β、δ和ω表示灰狼个体，其中α代表决策和管理狼群的个体，β和δ适应度低于α，ω为普通个体。GWO算法的具体行为有包围、捕猎和攻击。

1.1 包围行为

灰狼包围猎物[6]的数据模型可以表示为式(1)和式(2)。

D=|C·Xp(t)-X(t)|

(1)

X(t+1)=Xp(t)-A·D

(2)

式中，D表示狼群与猎物的距离,A=2a·r1-a，C=2·r2，t表示迭代的次数,Xp和X分别表示猎物和狼群的位置,r1、r2为随机量，其取值范围为[0,1],a的取值范围为[0,2]。

1.2 捕猎行为

假设α、β、δ代表灰狼个体的全局最优解、第二解和第三解，对其进行优化定位[7]，则距离分别表示为式(3)—式(5)。

Dα=|C1·Xα-X|

(3)

Dβ=|C2·Xβ-X|

(4)

Dδ=|C3·Xδ-X|

(5)

式中，Dα、Dβ、Dδ表示个体α、β、δ与当前的位置X的近似距离，Xα、Xβ、Xδ依次表示全局最优解、第二解和第三解的位置；C1、C2、C3表示随机向量，其取值范围为[0,1]。X和X(t+1)表示分别为式(6)—式(8)和式(9)。

X1=Xα-A1·(Dα)

(6)

X2=Xβ-A2·(Dβ)

(7)

X3=Xδ-A3·(Dδ)

(8)

(9)

式中，X(t+1)表示更新解，A1、A2、A3表示随机量。

1.3 攻击行为

攻击是狼群捕食行为的最后阶段，通过调节参数a即可实现攻击。如果|A|≤1，狼群接近猎物，集中攻击猎物(X*,Y*)；反之，狼群逐渐远离猎物。

2 深度置信网络

DBN是由一系列受限玻尔兹曼机(Restricted Boltzmann Machine，RBM)堆叠而成的一种概率型深度学习网络[8]。RBM由一层显层v和一层隐层h组成，其中显层v和隐层h二者的作用分别是用于输入数据和作为特征收集器。RBM结构如图1所示。

图1 RBM结构图

假若给定RBM的(v,h)的状态，那么其能量函数如式(10)。

(10)

式中，θ={w,a,b}为待求参数，其中a和b分别为为显层和隐层偏置，w为显层和隐层间的连接权值。当θ确定后，根据能量函数可计算出(v,h)的联合概率分布[9]，如式(11)，

(11)

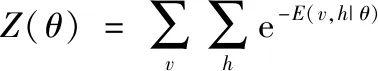
当显层v状态确定后，隐层单元激活概率为式(12)，

(12)

当隐层h状态确定后，显层单元激活概率为式(13)，

(13)

当训练样本数为K时，通过求解对数似然函数最大化问题，可以确定参数θ，对数似然函数最大化问题的目标函数[10]如式(14)给出，

(14)

式中,maxL(θ)由随机梯度法求取。

通过Gibbs采样重复，可以得到RBM参数的更新规则如式(15)。

Δwij=ε(〈vihj〉data-〈vihj〉recon)

Δai=ε(〈vi〉data-〈vi〉recon)

(15)

Δbj=ε(〈hj〉data-〈hj〉recon)

式中,ε为RBM学习速率,〈·〉data和〈·〉recon分别为输入数据和重构后数据的数学期望。

3 基于GWO-DBN的网络流量异常识别

3.1 目标函数

网络流量异常识别本质上是一种多模式识别问题。针对DBN模型性能受到参数θ={W，a，b}选择的影响[11]，本文运用GWO算法优化选择DBN模型的参数θ={W，a，b}，目标函数选择均方根误差,如式(16)。

s.t.W∈[Wmin,Wmax]

(16)

a∈[amin,amax]

b∈[bmin,bmax]

式中，k为训练样本数量,x(k)和p(k)分别为DBN模型的实际值和预测值,Wmin、Wmax，amin、amax和bmin、bmax分别为W、a和b的下限和上限。

3.2 算法流程

基于GWO-DBN的医院网络流量异常识别算法流程描述如下。

1)读取医院网络流量异常数据，划分训练集和测试集，对数据进行归一化处理如式(17)。

(17)

式中，x′表示归一化后的数据,La、Lb分别表示归一化之后的最小值和最大值，此处均取值为1,x、xmax和xmin表示原始数据、原始最大值、原始最小值。

2)GWO算法参数初始化处理：最大迭代次数Max gen、种群规模N、搜索维数D。随机产生灰狼初始种群个体，每个灰狼种群个体位置为ELM模型参数组合(W、a、b)。

3)计算不同的灰狼个体的适应度fi，并对其进行排序，选出排名前三的个体，分别标记为Xα、Xβ和Xδ。

4)根据式(3)—式(5)计算α、β、δ与ω之间的距离，按照式(6)—式(8)和式(9)对猎物和狼的位置进行更新。

5)更新参数a、参数A、参数C。

6)判断算法执行是否符合终止条件；如果已经达到最大的迭代次数，输出DBN模型的最优参数解，否则返回继续执行步骤3。

7)将最优参数(W、a、b)代入DBN模型进行医院网络流量异常识别。基于GWO-DBN的医院网络流量异常识别流程如图2所示。

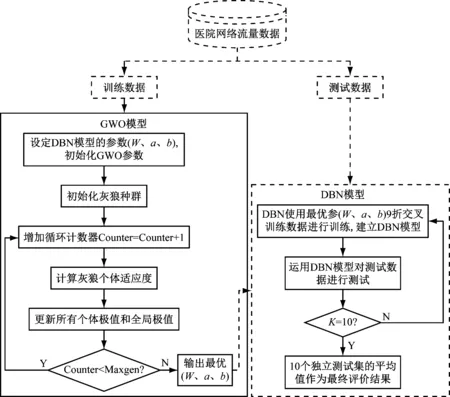
图2 基于GWO-DBN的医院网络流量异常识别流程图

4 实验与结果分析

4.1 数据来源

为了验证GWO-DBN进行医院网络异常流量识别的效果，在操作系统为Windows10、中央处理器为Intel core I5 2.4 GHz、内存8 GB的个人计算机上选择MATLAB2015(a)进行仿真实验。选择KDD CUP99标准数据集为研究对象[12]，其中网络异常流量类型分为正常样本、DoS、Probe、U2R和R2L，每个样本包括34个数值型字段和7个符号型字段，共41个特征。不同样本含义与分布如表1所示。

表1 样本含义与分布

4.2 评价指标

为了说明医院网络异常流量识别的效果，选择准确率(accuracy，ACC)、检测率(Detection Rate，DR)和误报率(False Alarm Rate，FAR)作为评价指标,如式(18)—式(20)。

(18)

(19)

(20)

式中，TP、TN分别为异常流量和正常流量被正确识别的样本数量,FP、FN分别为正常流量和异常流量被错误识别为异常流量、正常流量的样本数量。

4.3 结果分析

为了验证GWO-DBN进行医院网络异常流量识别的效果，对比GWO-DBN、粒子群算法优化DBN(PSO-DBN)和DBN算法的识别效果，表2所示为不同算法的参数。PSO-DBN、GWO-DBN的收敛曲线分别如图3(a)、图3(b)所示，通过对比分析可以看出GWO-DBN算法的收敛效果更好，迭代5次后即开始收敛。

表2 参数设置

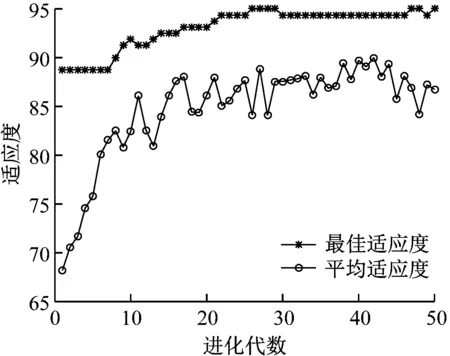
(a)PSO-DBN

GWO-DBN、PSO-DBN和DBN识别结果如表3所示，识别结果对比分析如图4所示。

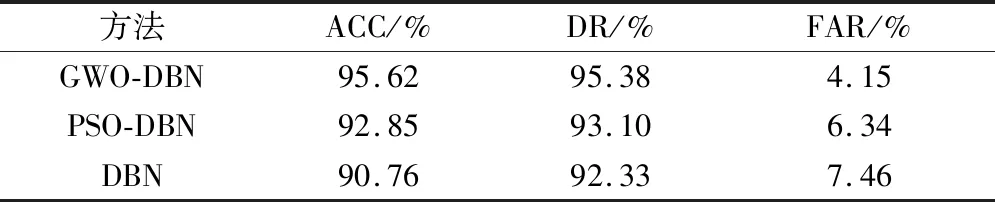
表3 识别结果

图4 ACC、DR和FAR对比图

由表3和图4可知，GWO-DBN的准确率(ACC)为97.62%，优于PSO-DBN的92.85%和DBN的90.76%。GWO-DBN的检测率(DR)为95.38%，优于PSO-DBN的93.10%和DBN的92.33%。GWO-DBN的误报率(FAR)为4.15%，优于PSO-DBN的6.34%和DBN的7.46%。由ACC、DR以及FAR 3个评价指标的对比结果可知，GWO-DBN进行医院网络异常流量识别具有更高的准确率、检测率和更低的误报率。

5 总结

为了提高医院网络异常流量识别的精度，针对DBN模型性能受权值和偏置参数的影响，运用灰狼算法对DBN模型的权值和偏置进行优化选择，提出一种灰狼算法优化DBN的医院网络异常流量识别方法。研究结果表明，GWO-DBN进行医院网络异常流量识别具有更高的准确率、检测率和更低的误报率。