涉及拟反向强单调算子零点的一个弱收敛结果及其应用
杨延涛,陈晶晶,周海云
(1.延安大学数学与计算机科学学院,陕西 延安 716000;2.河北师范大学数信学院,河北 石家庄 050024)
0 引言
设H为 实 的Hilbert空 间,·,·和‖·‖分别表示H中的内积和范数,A:H→H为算子。
零点问题(zero point,ZP)是非线性算子理论的重要研究方向之一,即寻求一点x*∈H,满足

各类算子的零点问题在诸如控制论、最优化理论、信号处理、图像恢复、机器学习和交通运输等领域具有广泛的应用,是求解许多应用科学实际问题的有力工具[1-8]。
求解零点问题的经典方法是最速下降法(steepest descent method,SDM):

其中,{tn}⊂(0,1)是满足某种条件的数列。
如果算子A:H→H是L-Lipschitz连续且强单调的,{tn}满足:

则由SDM产生的序列{xn}依范数收敛于A的唯一零点[9]。那么当A是L-Lipschitz连续的拟反向强单调算子时,由SDM产生的序列{xn}是否收敛于A的某个零点?
为此,本文采用新的分析技巧,首先证明弱收敛定理,然后运用所建立的弱收敛定理求解一类分裂公共不动点问题(SCFPP)。所得结果改进了文献[10-11]的相关结果。
1 预备知识
设H为 实Hilbert空 间,A:H→H为 算 子。N(A):={x∈H:Ax=0}表示A的核。
定义1如果存在ν>0和N(A)≠∅,满足

则称A:H→H为拟ν-反向强单调的。
定义2如果存在L≥1,使得

则称A:H→H为L-Lipschitz连续的。
定 义3如 果 对 任 意 的{xn}⊂H,xn⇀x和Axn→0(n→∞),有x∈N(A),则称A:H→H在原点为次闭的。
定义4如果对任意的x*∈C,恒有
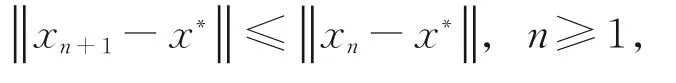
则称序列{xn}⊂H关于C⊂H为Fejér单调的。
定义5设C为H中的非空闭凸子集,x∈C,定义 算 子PC:H→C为PC x=x0,其 中x0∈C满 足称PC为从H到C上的距离投影算子。
引理1[9]设H为实Hilbert空间,则

引理2设算子A:H→H为拟ν-反向强单调的,则N(A)≠∅闭凸。
证明首先,由定义1知,N(A)≠∅。
然后,证明N(A)是闭的。
任取{xn}⊂N(A),xn→x(n→∞),则

由定义1知,

因xn→x(n→∞),故

从而Ax=0,即x∈N(A),因此,N(A)是闭的。
最后,证明N(A)是凸的。
任取xi∈N(A)(i=1,2),t∈(0,1),记

由定义1知,

用(1-t)与t分别乘以式(6)和(7)两侧,然后两式相加,可得

故

即xt∈N(A),因此N()A是凸的。
引理3[9]设{an}和{bn}为2个正实数列,满足an+1≤an+bn,n≥1,如 果存在。
引 理4[9]设C为H中 的 非 空 闭 凸 子 集,{xn}⊂H关 于C为Fejér单 调 序 列。如 果ω(xn)⊂C,则xn⇀x(n→∞),且其中存在{xnj}⊂{xn},使得xnj⇀x},称为{xn}的w-极限集。
2 主要结果
定理1设H为实Hilbert空间,算子A:H→H为L-Lipschitz连续拟ν-反向强单调的。假设A在原点是次闭的,如果{tn}满足条件(C1)和(C2),则由SDM产生的序列{xn}弱收敛于
证明由引理2知,N(A)≠∅闭凸;由定义5知,PN()A唯一确定。对任意的x∈N(A),由引理1、SDM及定义1,有

其中,对充分大的n,tn<ν。可得
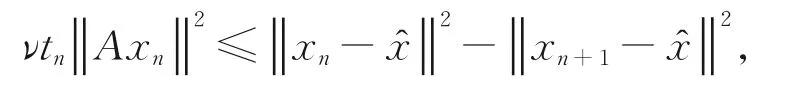
因此,{xn}关于N(A)是Fejér单调的,且对充分大的n0,有

由条件(C2)知,

为 保 证Axn→0(n→∞),只 需 证存在即可。
事实上,由于算子A是L-Lipschitz连续的,由SDM,可得

由条件(C1)知,对n≥1,可得

由式(8)和式(9),对n≥n1,有

由 于3L故由引理3知,存在,所以

由于算子A在原点是次闭的,故
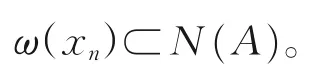
再由引理4,可知

3 应用
将定理1应用于求解一类分裂公共不动点问题。设H1和H2为2个实Hilbert空间,S:H1→H1和T:H2→H2为2个 映 像,分 别 满 足Fix(S)≠∅和Fix(T)≠∅,A:H1→H2为有界线性算子。寻找一点p∈Fix(S),满足

用Ω表示式(10)的解集,即
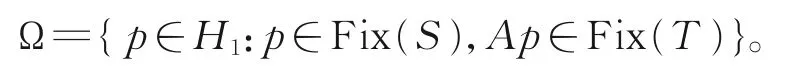
定 义6设H为 实Hilbert空 间,如 果Fix(T)≠∅且存在k<1,使得

称T:H→H为k-半压缩映像。
注1当k=-1时,称T为定向的或拟firmly-非扩张的;当k=0时,称T为拟非扩张的;当k=1时,称T为拟伪压缩的。因此,k-半压缩映像是一类十分丰富的映像,具有重要的学术价值与广泛的应用前景。
定理2设S:H1→H1为k1-半 压 缩 映 像,T:H2→H2为k2-半 压 缩 映 像,S和T均L-Lipschitz连续。I-S和I-T均在原点次闭。假设{tn}满足条件(C1)和(C2),定义序列{xn}:

如果Ω≠∅,则由式(12)产生的序列{xn}弱收敛于x*∈Ω,且
证明定义算子B:H1→H1为

则式(12)可转化为

要证明定理2成立,只需证明算子B满足定理1中的全部条件。
首先,证明算子B是Lipschitz连续的拟ν-反向强单调的。
由于S和T均L-Lipschitz连续的,故对任意的x,y∈H1,有
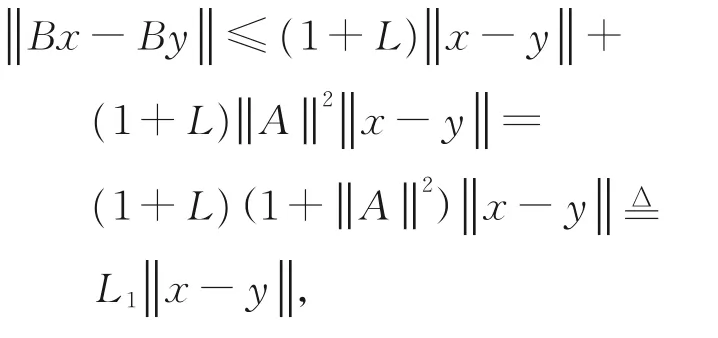
其中,L1=(1+L)(1+‖A‖2)>1,因此,算子B是L1-Lipschitz连续的。
下面证明Ω=N(B)。
一方面,对任意的p∈Ω,有p=Sp,Ap=TAp,从而

因此

反 之,对 任 意 的p∈N(B),有Bp=0。因 为Ω≠∅,故取x*∈Ω,由式(11)和引理1,得
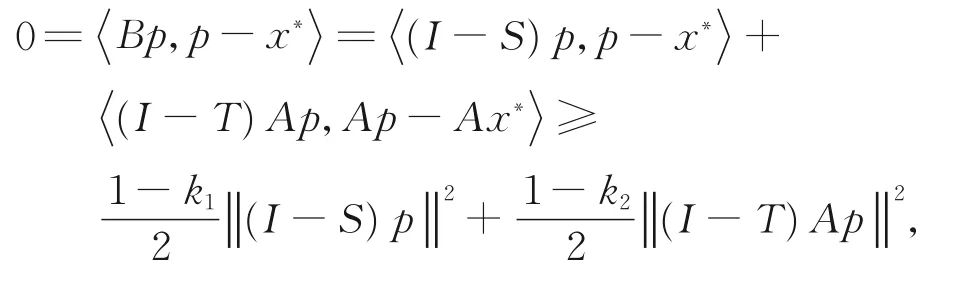

从而p∈Ω,即N(B)⊆Ω,因此N(B)=Ω≠∅。
然后,证明算子B是拟ν-反向强单调的。
对于任意p∈N(B)=Ω和x∈H1,由 引理2和式(11),得
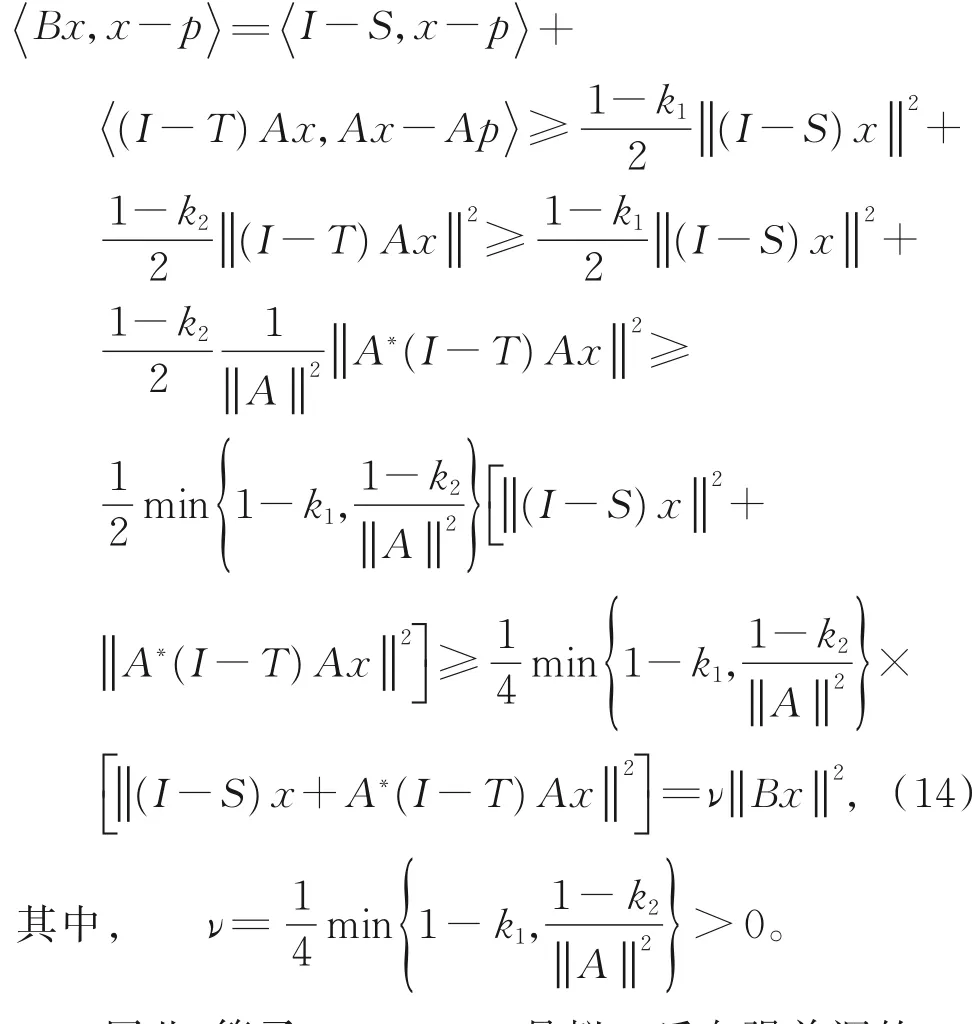
因此,算子B:H1→H1是拟ν-反向强单调的。
最后,证明算子B:H1→H1在原点是次闭的。
对 任 意 的{xn}⊂H1,有xn⇀x(n→∞),Bxn→0(n→∞)。由式(14)知,

由于I-S和I-T在原点是次闭的,故

从而Bx=0。
至此,满足定理1的全部条件。
由定理1知,{xn}弱收敛于x*∈N(B)=Ω,且

证毕!
注2一方面,将步长序列减弱为tn→0(n→∞);另一方面,将映像推广为k-半压缩映像,其中k<1,而在文献[11]中,k∈[0,1)。如果取k=-1,便可推得文献[10]的主要结论。

