基于五元半偏减法集对势的区域农业旱灾脆弱性评价

金菊良 孔令茹 崔 毅 周戎星 陈梦璐 宁少尉

(1.合肥工业大学土木与水利工程学院, 合肥 230009; 2.合肥工业大学水资源与环境系统工程研究所, 合肥 230009)

0 引言

在全球气候剧烈变化和经济社会高速发展的背景下，干旱事件频发，旱灾损失巨大，亟需开展基于物理成因的旱灾风险防控理论与实践研究[1-3]。其中旱灾风险评估是旱灾风险防控的基础，特别是承灾体脆弱性是将干旱事件危险性转换为旱灾损失风险的核心环节[4]，准确评估承灾体脆弱性对实现旱灾风险防控十分关键[5-7]。农业系统是干旱事件最直接的承灾体，旱灾造成的损失常凸显于农业系统之中。据《中国水旱灾害公报》统计，2000年以来，我国年均因旱粮食损失190.2亿kg、因旱经济作物损失251.6亿元[8]。农业旱灾问题已严重威胁我国粮食安全和脱贫攻坚[9-11]。因此，定量评价农业旱灾脆弱性、准确识别影响农业旱灾脆弱性的关键要素及其发展趋势对调整农业种植结构、优选抗旱减灾适应性策略，充分保障区域农业可持续发展具有重要科学意义[5,12]。

近年来，国内外学者对区域农业旱灾脆弱性开展了大量研究。曹永强等[13]利用DPS中的投影寻踪综合评价法，对衡阳市7个县域的农业旱灾脆弱性进行了评价。李艳[14]在对河南省旱情评价的研究中，构建了基于集对分析理论的旱情评价模型。REIS等[15]提出了iSECA模型，通过MCDM技术计算脆弱性指数，GIS软件用于分类及绘制旱灾脆弱性分布示意图，并将其应用于圣保罗及塞阿拉州的福塔雷萨的旱灾脆弱性研究中。AHMADALIPOUR等[16]通过采集1960—2015年社会经济统计数据，计算了46个非洲国家的旱灾脆弱性指数，并预测了2020—2100年的旱灾脆弱性。JIANG等[17]利用扩展灰色关联分析法对2009年中国31个省市的农业旱灾脆弱性进行了评估。金菊良等[18]采用灰色关联度和联系数耦合的方法对蚌埠市农业旱灾脆弱性进行了评价和诊断研究。其中，集对分析法可从同异反3方面深入探讨评价样本、评价子系统、评价指标值与评价标准等级之间的模糊不确定性关系，在处理确定性和不确定性问题中具有独特优势，方法客观、计算方便，分析问题全面，在具有不确定性和复杂性的典型旱灾脆弱性评估问题中较为适用。目前针对农业旱灾脆弱性研究成果中多是对旱灾脆弱性进行静态评价，对区域农业旱灾脆弱性发展趋势的动态评价分析研究较少，尚缺乏有效识别诊断农业旱灾脆弱性影响因素的方法，且现有的三元半偏减法集对势[19]不适应复杂系统多等级问题。为有效评价区域农业旱灾脆弱性动态发展趋势、准确识别脆弱性系统中具有较大影响的指标，本文综合考虑五元联系数的结构形式，在三元半偏减法集对势[19]的基础上，推导提出五元联系数的伴随函数——五元半偏减法集对势，并将该伴随函数应用于区域农业旱灾脆弱性趋势分析中，以蚌埠市2001—2010年农业旱灾脆弱性评价为研究对象，建立评价指标体系，采用联系数对农业旱灾脆弱性进行动态评价，再利用五元半偏减法集对势诊断影响脆弱性的子系统及关键因素。

1 评价模型构建

基于五元半偏减法集对势的区域农业旱灾脆弱性评价模型的建立包括4个步骤：

步骤1：在综合分析农业旱灾脆弱性评价与诊断内涵的基础上，结合农业旱灾脆弱性已有研究[5,18,20]，构建区域农业旱灾脆弱性评价指标体系{xj|j=1,2,…,nj}和评价标准等级{skj|k=1,2,…,nk;j=1,2,…,nj},相应的评价指标样本数据记为{xij|i=1,2,…,ni;j=1,2,…,nj}。其中，xj为区域农业旱灾脆弱性评价指标体系中的第j个评价指标，nk、ni、nj分别表示评价标准等级个数、评价样本个数和评价指标个数；skj为区域农业旱灾脆弱性评价指标体系中指标j的第k个评价标准等级，xij为评价样本i指标j的样本值。为使评价等级适用于五元联系数的计算，本文将脆弱性评价指标标准等级取为弱、较弱、中等、较强和强5个级别，1级为“弱”，5级为“强”，其余类推，即nk=5。其中，农业旱灾脆弱性越强，说明其抵御干旱威胁的能力越低。

步骤2：在根据已有评价样本i指标j的样本值xij与评价样本标准等级skj之间接近程度计算区域农业旱灾脆弱性评价样本的指标值联系数uijk(i=1,2,…,ni;j=1,2,…,nj;k=1,2,…,5)[21-23]分段函数的基础上，作进一步改进。其中，uijk为样本i中指标j的值与第k个评价指标的指标值联系数。现有指标值联系数的分段函数[21-23]与改进后的指标值联系数分段函数计算示意图(以正向指标为例)如图1所示，图1a～1e为现有指标值联系数的分段函数[21-23]，图1a为样本值xij与评价样本标准等级s1j处于同一等级，图1e为样本值xij与评价样本标准等级s5j处于同一等级，其余类推。其中，s0j为指标j等级1级的一端点临界值，s1j为评价指标j等级1级与2级的临界值，s2j为评价指标j等级2级与3级的临界值，s3j为评价指标j等级3级与4级的临界值，s4j为评价指标j等级4级与5级的临界值，s5j为指标j等级5级的一端点临界值。图1a～1e中，评价样本i指标j的样本值xij与评价样本标准等级skj若处于同一等级中则该指标值联系数uijk为1；若处于相隔等级中则uijk为-1；若处于相邻的等级中则uijk∈[-1,1]，xij越接近于等级skj则uijk越趋近于1，xij越接近于与等级skj相隔的等级则uijk越趋近于-1[23]。图1f～1j为对应的改进后的指标值联系数的分段函数。

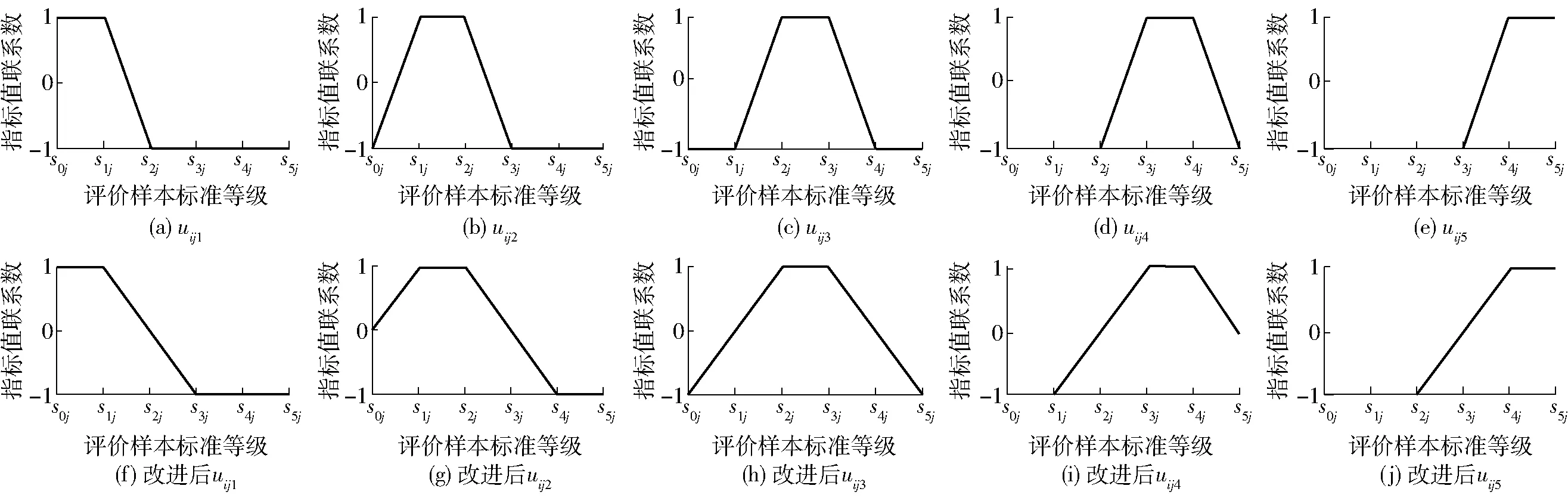
图1 现有和改进后指标值联系数的分段函数示意图(以正向指标为例)Fig.1 Schematics of existing index connection number piecewise function and improved piecewise function (positive index)

为避免在计算指标值五元联系数时出现多个零的问题，本研究通过放缓现有指标值联系数的分段函数中相邻两个等级的斜率(比较图1a～1e)，缩短联系数对立度区间，丰富样本值与评价标准等级之间单指标联系数的物理意义。在改进后的分段函数(图1f～1j)中：若处在同一等级中则uijk=1；若处在相隔两个或以上等级中则uijk=-1；若处于相邻的两个等级中则uijk∈[-1,1]，xij越接近于等级skj则uijk越趋近于1，xij越接近于与等级skj相隔的等级则uijk越趋近于-1。其中，图1f为样本值xij与评价样本标准等级s1j处于同一等级，图1j为样本值xij与评价样本标准等级s5j处于同一等级，其余类推。综合考虑五元联系数的结构特性，计算公式为

(1)

(2)

(3)

(4)

(5)

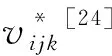
(i=1,2,…,ni;j=1,2,…,nj;k=1,2,…,5)

(6)

归一化式(6)可得农业旱灾脆弱性评价指标值联系数分量[22-23]

(7)

式中vijk——样本i的指标j与第k个等级的指标值联系数分量

由指标值联系数分量vijk可得评价指标值五元联系数uij[21-23]为

uij=vij1+vij2I1+vij3I2+vij4I3+vij5J

(8)

式中I1、I2、I3——差异度系数

J——对立度系数

由式(8)可得农业旱灾脆弱性评价样本i的指标值联系数ui[22]为

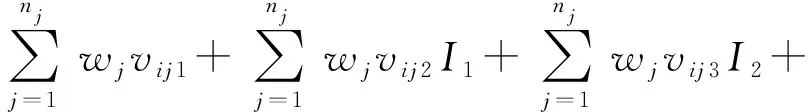
(9)

式中vik——评价样本i与第k个等级的指标值联系数分量，k=1,2,3,4,5

wj——指标j的权重

步骤3：确定区域农业旱灾脆弱性评价等级。采用级别特征值法[24]计算指标值联系数对应样本的区域农业旱灾脆弱性评价等级值，计算评价指标值联系数对应样本i的农业旱灾脆弱性评价等级值h(i)及样本i第j个指标的农业旱灾脆弱性评价等级值h(i,j)[19,23]，计算式为

(10)

(11)

步骤4：构建、计算区域农业旱灾脆弱性评价样本联系数的五元半偏减法集对势，判别区域农业旱灾脆弱性的发展趋势，识别影响区域农业旱灾脆弱性的关键指标[22]。

文献[19]在集对分析理论研究的基础上，对集对势、偏联系数[25-26]这两种主要的联系数伴随函数方法比较分析，构造了三元联系数u=a+bI+cJ(其中，I为差异度系数)的一种新的伴随函数——三元半偏减法集对势[19]，计算式为

(12)

式中a——同一度b——差异度

c——对立度

本研究在三元半偏减法集对势的基础上，考虑五元联系数u=a+b1I1+b2I2+b3I3+cJ的结构形式及其同一度a、对立度c以及偏同差异度b1、不确定性差异度b2、偏反差异度b3对集对系统联系数发展趋势的影响，综合考虑五元联系数各个分量的具体内涵及相互作用，通过五元、三元联系数结构类比的方式，提出五元联系数的半偏减法集对势公式为

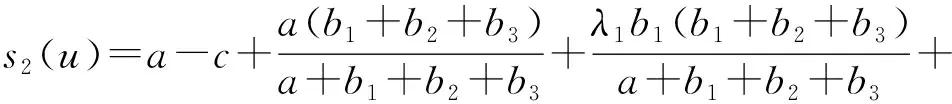
(13)

式中λ1、λ2——系数

为了处理复杂系统多等级问题，将三元联系数半偏减法集对势推广到五元联系数[21]：将三元联系数u=a+bI+cJ中的差异度b进一步细化为偏同差异度b1、不确定性差异度b2、偏反差异度b3；五元联系数u=a+b1I1+b2I2+b3I3+cJ中各分量对集对系统的发展趋势具有不同的影响程度，同一度a与对立度c是完全对立的确定性关系，对集对系统发展趋势影响最大；差异度b1、b2、b3中b1与b3之间的对立强度稍弱于a与c，并且b1、b3对系统发展趋势的影响程度也较a、c弱，而b2对系统发展趋势影响具有较大的不确定性，对集对系统发展趋势的影响较b1、b3相对中立。

依据文献[25-26]中偏联系数的观点，同一度a可认为是从a、b1、b2、b3正向发展而来，故要将b1、b2、b3中的同一部分发展到a上，可将差异度b1+b2+b3作为一个整体，并将其按照a/(a+b1+b2+b3)的比例分配到同一度方向上，同理，偏同差异度b1可看作是同一性稍弱的a，也可认为是从a、b1、b2、b3正向发展而来，可将b1+b2+b3作为一个整体，按照λ1b1/(a+b1+b2+b3)的比例分配到同一度方向上；类似地，对立度c可认为是从b1、b2、b3、c负向发展而来，故应将b1、b2、b3、c中的对立部分发展到c上，可将差异度b1+b2+b3作为一个整体，并将其按照c/(c+b1+b2+b3)的比例分配到对立度方向上，同理，偏反差异度b3可看作是对立性稍弱的c，也可认为是从b1、b2、b3、c负向发展而来，故应将b1、b2、b3中的对立部分发展到b3上，可将b1+b2+b3作为一个整体，按照λ2b3/(c+b1+b2+b3)的比例分配到对立度方向上去。其中，λ1∈[0, 1]，λ2∈[-1, 0]。考虑到差异度b1、b2、b3中b1、b3对集对系统整体发展趋势的影响程度稍弱于a、c，本研究参照文献[27]按照平均情况取λ1=0.5，λ2=-0.5。另外，当b1+b2+b3=0时显然有s2(u)=a-c。因此，可推导出上述五元半偏减法集对势计算公式。综上所述，提出的五元半偏减法集对势可进一步表示为

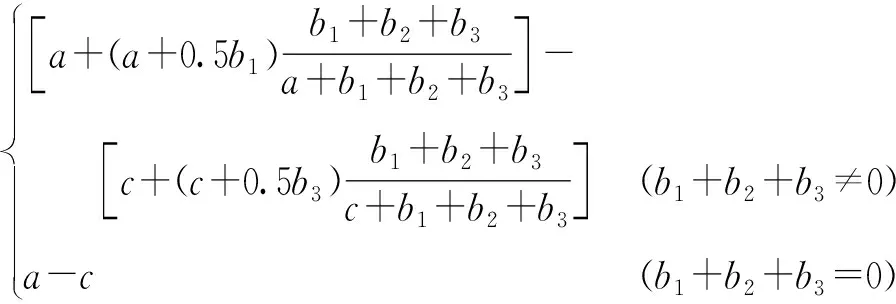
(14)

其中，a、b1、b2、b3、c分别对应式(1)～(5)中的uij1、uij2、uij3、uij4、uij5。推导可知s2(u)∈[-1, 1]，依据“均分原则”[21-23]可将s2(u)取值区间划分为5个集对势级：反势(s2(u)∈[-1, -0.6))、偏反势(s2(u)∈[-0.6, -0.2))、均势(s2(u)∈[-0.2, 0.2])、偏同势(s2(u)∈(0.2, 0.6])、同势(s2(u)∈(0.6, 1])。当评价指标的半偏减法集对势处于反势或者偏反势时，认为该指标是导致区域农业旱灾脆弱性等级较差的主要因素，该指标所代表的方向是今后脆弱性发展过程中应重点关注的调控方面[18,27]。式(14)是依据三元半偏减法集对势类推出的一种新的联系数伴随函数，为进一步验证其合理性，本文比较了五元半偏减法集对势与五元减法集对势s3(u)[27]在数值上的接近程度，二者的平均绝对误差d为

(15)

(16)

式中um——随机模拟五元联系数

M——随机模拟五元联系数um的个数

经大量随机模拟实验可得，当M分别取103、104、105和106时，d分别为0.015 9、0.015 9、0.016 0、0.016 1。这说明式(14)的五元半偏减法集对势在数值上非常接近式(16)的五元减法集对势，二者皆可用于判断宏观确定性层次上集对系统的总体发展趋势[19,22,27]。根据文献[18-19,27]可知，针对联系数的关系结构特征[28]，构造五元减法集对势的基本思想就是合理地把兼有确定性及不确定性变化趋势信息的五元联系数转换为确定性的总体发展趋势，即将差异度b1+b2+b3按照a/(a+b1+b2+b3+c)、c/(a+b1+b2+b3+c)的比例分别分配到同一度a和对立度c中；将差异度b1+b2+b3按照b1/(a+b1+b2+b3+c)、b3/(a+b1+b2+b3+c)的比例分别分配到偏同差异度b1和偏反差异度b3中。从偏联系数的思想看，要把b1、b2、b3中的同一部分发展到a上，可知原来的a是从a、b1、b2、b3正向发展而来的，不包括对立度c，所以b1+b2+b3这一部分发展到a上的比例取a/(a+b1+b2+b3)比取a/(a+b1+b2+b3+c)更为合理；同理，要把b1、b2、b3中的对立部分发展到c上，可知原来的c是从b1、b2、b3、c负向发展而来的，不包括同一度a，所以b1+b2+b3这一部分发展到c上的比例取c/(b1+b2+b3+c)比取c/(a+b1+b2+b3+c)更为合理。同样，从偏联系数的思想看，要把b1、b2、b3中的弱同一部分发展到b1上，可知原来的b1是从a、b1、b2、b3正向发展而来的，不包括对立度c，所以b1+b2+b3这一部分发展到b1上的比例取λ1b1/(a+b1+b2+b3)比取λ1b1/(a+b1+b2+b3+c)更为合理；同理，要把b1、b2、b3、c的弱对立部分发展到b3上，可知原来的b3是从b1、b2、b3、c负向发展而来的，不包括同一度a，所以b1+b2+b3这一部分发展到b3上的比例取λ2b3/(b1+b2+b3+c)比取λ2b3/(a+b1+b2+b3+c)更为合理。这里提出的五元半偏减法集对势整体上利用减法集对势的思路把差异度不确定性项转换为确定性的同一度项和对立度项，同时结合偏联系数的思路实现这种转换，其解释性更强、识别结果更可靠，能够灵敏反映评价样本指标值联系数的变化、定量判别宏观层面上集对系统的相对确定性程度及其趋势变化，在处理复杂系统多等级评价问题中具有更为广泛的应用前景。

2 实例分析

根据文献[18]中蚌埠市农业旱灾脆弱性评价指标体系、评价指标权重和相应标准等级，整理2001—2010年的《安徽省统计年鉴》资料获得安徽省蚌埠市2001—2010年的评价样本数据，采用式(1)～(5)计算23个指标的五元联系数分量，可得蚌埠市2001—2010年农业旱灾脆弱性评价样本各子系统的联系数分量，再由式(6)～(11)计算得到这些联系数所对应的脆弱性评价等级，并由式(14)计算脆弱性评价样本各子系统的五元半偏减法集对势，见表1。

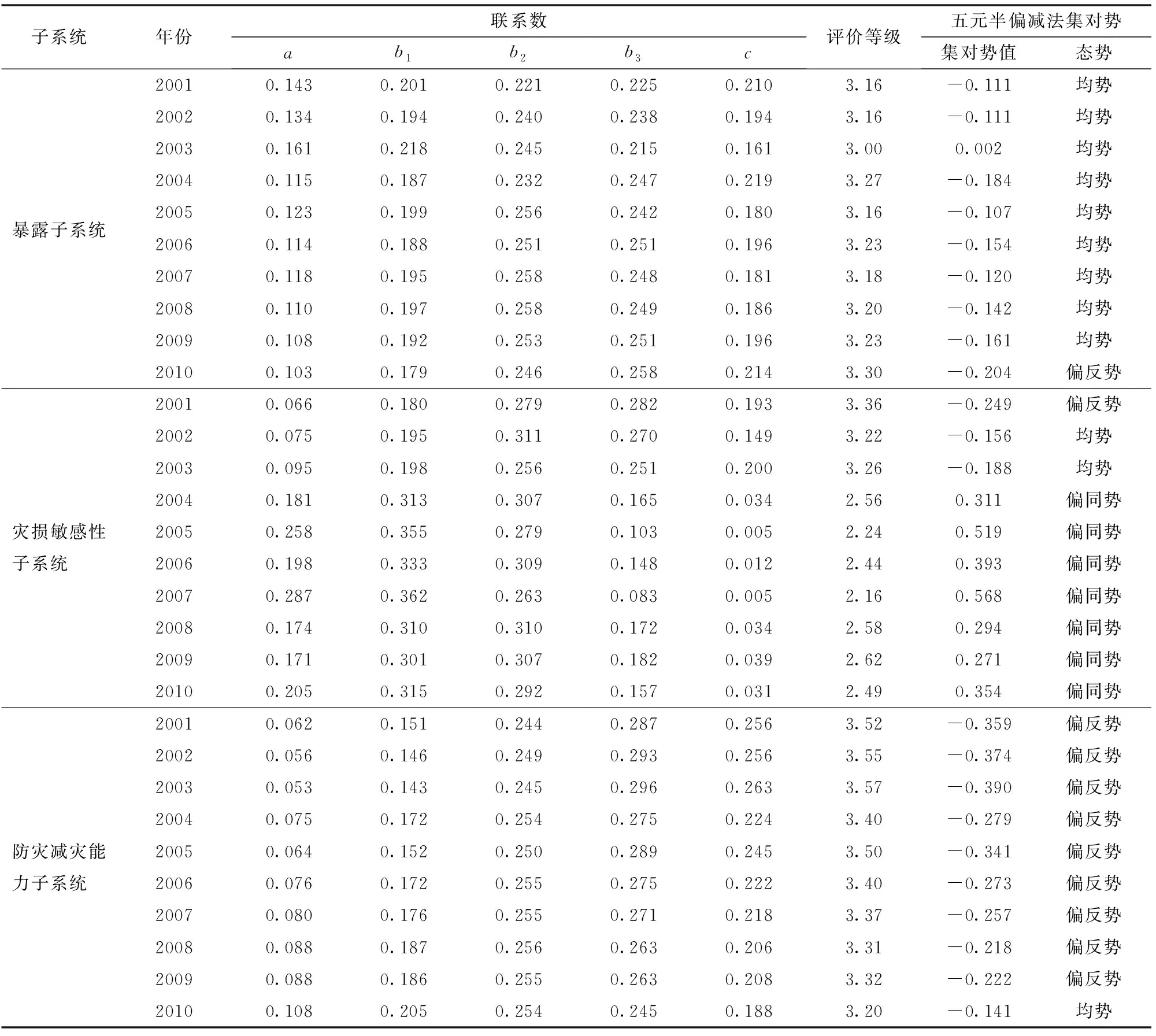
表1 蚌埠市农业旱灾脆弱性各子系统联系数分量、评价等级及五元半偏减法集对势Tab.1 Connection number components, evaluation grades and five-element semipartial subtraction set pair potential for each subsystem of agricultural drought vulnerability in Bengbu City

由表1可知，在蚌埠市农业旱灾脆弱性评价系统中，暴露子系统等级波动较小，2001—2009年处于均势状态，2010年处于偏反势，评价等级在3.00～3.30之间，2007年之后暴露程度呈缓慢增大的趋势。灾损敏感性子系统整体趋势向半偏减法集对势值增加的方向发展，其发展与蚌埠市农业旱灾脆弱性整体改善的情况一致。整体趋势波动较大，2001年处于偏反势，2002—2003年处于均势，而2004年之后逐渐变为偏同势，评价等级在2.16～3.36之间，其评价等级呈下降趋势，评估结果呈现逐年向好趋势。防灾减灾能力子系统趋势沿降低脆弱性方向发展，整体上升趋势较为平缓，在2001—2009年处于偏反势，2010年处于均势状态，评价等级在3.20～3.57之间，说明与农业旱灾相关的防灾减灾措施发展仍有较大的发展空间，积极推进相关措施的实施对降低农业旱灾脆弱性可以起到较大的促进作用。由上述暴露、灾损敏感性和防灾减灾能力子系统评价结果进行加权和综合得到的蚌埠市2001—2010年农业旱灾脆弱性评价等级，与文献[18]给出的灰色关联度和联系数耦合的脆弱性评价模型、模糊综合评价方法的评价等级计算值一致，见图2。

图2 不同方法的蚌埠市农业旱灾脆弱性评价结果对比Fig.2 Comparison of different evaluation methods for agricultural drought vulnerability assessment results in Bengbu City

由图2可知，2001—2010年蚌埠市农业旱灾脆弱性整体呈降低趋势，农业系统对干旱威胁的抵御能力逐渐增强。本文评价方法较模糊综合评价法所计算得到的评价等级整体上略微偏小。模糊综合评价法利用最大隶属度原则对旱灾脆弱性等级进行判断，而对于综合隶属度相差不大、旱灾脆弱性等级不明确的年份，利用最大隶属度原则可能存在评价等级偏大问题，故本文评价方法更为合理。由于本研究提出放缓现有指标值联系数的分段函数中相邻两个等级的斜率，缩短了联系数对立度区间，使得本文评价方法计算所得的旱灾脆弱性评价结果较灰色关联度和联系数耦合评价模型更加平稳。具体来说本文评价方法与灰色关联度和联系数耦合评价模型所得2001—2003年脆弱性等级均大于3级，但程度逐渐减弱，蚌埠市农业系统抵御旱灾的能力逐渐增强。五元半偏减法集对势计算所得脆弱性等级变化整体低于灰色关联度和联系数耦合评价模型(图2)。两种方法所得2004—2010年脆弱性等级均小于或等于3级，但五元半偏减法集对势计算所得的等级变化整体高于灰色关联度和联系数耦合评价模型(图2)。灰色关联度和联系数耦合评价模型计算的2009年蚌埠市农业旱灾脆弱性评价等级为3.144，与其整体评价等级变化趋势不一致。因此，本文方法所得区域农业旱灾脆弱性评价结果更加稳定合理、可靠度更高。

为进一步分析蚌埠市农业抵御干旱威胁的能力变强的主要原因，由式(14)计算23个评价指标2001—2010年的五元半偏减法集对势值，据此识别诊断对蚌埠市农业旱灾脆弱性变化程度有较大影响的主要指标。选取2001—2010年五元半偏减法集对势变化较大的评价指标进行分析，结果如图3所示。

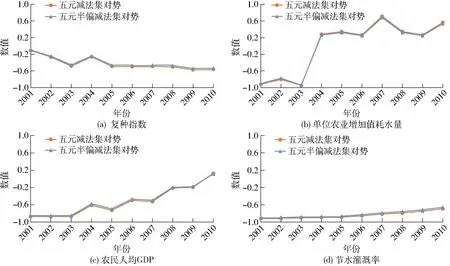
图3 2001—2010年蚌埠市农业旱灾脆弱性主要评价指标动态诊断分析结果Fig.3 Agricultural drought vulnerability dynamic diagnosis and analysis results of main indicators from 2001 to 2010 in Bengbu City

由图3可知，农业旱灾脆弱性诊断的4个主要指标的五元半偏减法集对势的计算值与五元减法集对势的计算结果非常接近。从图3a可看出，复种指数在2001年处于均势，2002—2010年一直处于偏反势，并有向反势发展的趋势。从时间上看，复种指数总体向着半偏减法集对势值减小的方向，即脆弱性增大的方向发展，抵御干旱威胁的能力逐渐减弱。结果表明，复种指数越高，同样面积耕地上的年内农作物种植量越大，需水量越大，使得承灾体暴露程度显著增加，农业旱灾脆弱性越高。因此，为降低区域农业旱灾脆弱性，应合理规划农作物种植期及种植范围，提升农业科学技术水平，提高当地农作物产出效率。由图3b可知，单位农业增加值耗水量在2001—2003年一直处于反势，此时段内的发展态势较为稳定，从2004年开始至2007年，态势由偏同势发展到同势，在2008—2010年处于偏同势。结果表明，单位农业增加值耗水量减少，是使得蚌埠市农业旱灾脆弱性呈改善趋势、抵御干旱能力增强的主要因素。因此，应大力改进推广节水灌溉新技术，增加农田灌溉水有效利用率，取代传统粗放式的灌溉方式。从图3c可看出，农民人均GDP呈逐年改善的趋势，在2001—2003年处于反势，2004年之后逐渐由偏反势转变为均势，农民人均GDP增加，其变化趋势与农业旱灾脆弱性状况有所改善的发展一致，说明蚌埠市农民收入有了缓慢的提升，农业产值增加。因此，增加农民人均GDP可向推进农业的规模化、提高农业现代化水平方向发展，从而降低区域农业旱灾脆弱性程度、增强农业系统抵御旱灾的能力。由图3d可知，节水灌溉率在2001—2010年一直处于反势，总体向着降低旱灾脆弱性的方向缓慢发展。结果表明，节水灌溉率越高，农业系统对干旱威胁的恢复能力越强，农业旱灾脆弱性越低。因此，应采取更为有效的方式提高节水灌溉率，改善节水措施，加大节水宣传教育力度，提升节水意识，大力推进农业节水改造，加强节水监督管理。

3 结论

(1)五元半偏减法集对势作为在三元半偏减法集对势基础上改进、拓展的一种应用范围更广的集对势方法，细化了评价指标所处的趋势强度，可更精确地反映出指标的变化趋势，蚌埠市农业旱灾脆弱性评价实证结果与实际情况较为接近。五元半偏减法集对势对于任何五元联系数均普遍适用，它充分考虑了多元联系数中差异度子项对集对系统发展趋势的影响，有效补充了半偏减法集对势在多元联系数中的应用，为处理复杂系统多等级定量评价与诊断问题提供了新的有效途径。

(2)进一步改进了用以计算评价指标样本值与评价标准等级之间联系数的分段函数，并将其应用于蚌埠市农业旱灾脆弱性的动态评价与诊断之中。应用结果表明，改进后的分段函数有效改善了五元联系数在计算时出现多个零值的问题，使得五元联系数的运算更加合理。

(3)蚌埠市农业旱灾脆弱性状况总体上呈缓慢改善的趋势。暴露子系统在2001—2009年处于均势，最终处于偏反势。灾损敏感性子系统发展趋势波动较大，在2001年处于偏反势，2002年之后由均势逐渐变为偏同势，其评估结果呈现逐年向好趋势。防灾减灾能力子系统在2001—2009年处于偏反势，2009年之后逐渐变为均势最终处于均势，评价等级皆大于3级。节水灌溉率、复种指数、农民人均GDP、单位农业增加值耗水量4个指标是影响蚌埠市农业旱灾脆弱性的最主要因素。这4个指标中，单位农业增加值耗水量的减少对蚌埠市农业旱灾脆弱性发展趋势的改善具有积极影响，而复种指数则存在着向反势态势发展的趋势，需采取合理有效的调控措施，可适当减少农作物的耕作(种植)面积，提高农作物产出效率。