基于鱼群算法的变电站巡检机器人路径规划研究

陈 曌

（湖北省电力装备有限公司，湖北 武汉 430000）

0 引 言

变电站在整个电力系统中承担着电能转换的任务。由于变电站是电力系统正常运转的关键，使得对变电站的日常巡检工作成为保障变电站安全高效运行的必要任务。传统的巡检方式要依靠大量的人力资源来完成，并且所处工作环境包含电磁辐射和部分户外的复杂气象条件，巡检任务的完成质量需要依靠具备一定经验的巡检人员[1,2]。传统变电站巡检方式不仅会增加成本，而且巡检质量参差不齐。随着巡检机器人在变电站巡检工作中的应用，巡检工作的难度和成本大大降低，能够保障变电站工作人员的人身安全。巡检机器人在变电站的运行要考虑到机器人的避障能力，同时为了保障机器人在巡检工作时的效率和缩短巡检时间，对机器人巡检路线的规划也极为重要[3-5]。

目前，有诸多学者对于变电站中机器人的路径规划有着一定的研究。张永涛等人采用枚举法对待配对节点进行匹配，并利用Fleury算法得到变电站全站全巡最佳路线[6]。对于待配对节点较多的情形，先采用K-means聚类算法将奇度节点根据其所在空间位置进行聚类分析,再利用枚举法对待配对节点分区域进行匹配优化。陈玮光等人基于改进遗传算法，对机器人巡检的路线进行优化,优化过程中将变电站平面图网格化处理便于计算，计及最高寻址效率，以行驶距离最短为优化目标[7]。路浩等人提出了一种基于改进蚁群算法的路径优化方法和基于贪婪思想聚类的巡检停靠点选取方法，通过蚁群算法迭代获得机器人的最优巡检路径、巡检停靠点序列以及各停靠点对应的测温点集[8]。杨希磊等人提出了目标为巡检时间最短的变电站巡检机器人功率分配模型，并使用粒子群算法进行模型求解[9]。徐明提出了一种基于改进深度强化学习的变电站机器人巡检路径规划方法。结合巡检机器人的运动模型，设计深度强化学习的动作和状态空间。将深度强化学习网络与人工势场相结合，重新构造深度强化学习的奖励函数，优化卷积神经网络结构[10]。

针对巡检机器人路径规划不佳的问题，通过一种鱼群算法，建立栅格化的变电站图，通过将机器人路径寻优问题转化为对鱼群觅食模拟和鱼群自身的生物行为，包括聚群行为、追尾行为以及随机行为进行最优解的求解。

1 路径规划模型

对于在路面上行进的机器人，可以将行进的场景简化为一个二维环境。通过栅格化将机器人实际工作的环境构建成一个栅格矩阵地图。栅格化的基本原理在于通过一个由机器人自身大小定义的二位单位栅格均匀构建与实际场地面积大小一致的栅格图。栅格化做法的目的是将实际的地图进行数字化，在栅格化后的地图中可标记出机器人潜在可行的运动路径和场地内实际存在的障碍物。在栅格化后的地图中给出目标机器人的出发点和目的地，通过算法形成多个由栅格号构成的路径。

栅格化操作后的变电站地图如图1所示。图中的黑色部分即为实际地图中障碍物所在的位置，在数字化表示中将被记为1；白色部分为机器人可行区域，会被记为0。

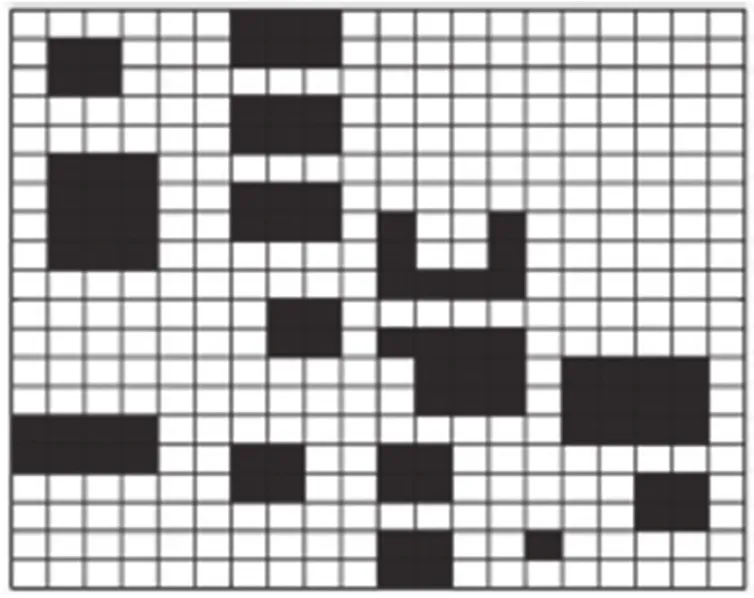
图1 栅格化操作后的变电站地图

为了表示机器人极大的行进自由度，定义机器人的行进方向。机器人的行进方向为8个方向，这种方式被称为八叉树搜索策略。以栅格图中的一个栅格为例，机器人在该栅格上可向8个方位的下一个栅格进行移动。机器人行进方向如图2所示。

图2 机器人行进方向

在栅格化后的矩阵中，每个栅格将会有自己的编号。如果矩阵为S×S，则矩阵最左上方的栅格记为1，该栅格往右则记为2，以此类推逐行进行标号直至最右下角的S2。当确定栅格图的坐标原点，后就可以计算出某个栅格点的距离。其计算公式为

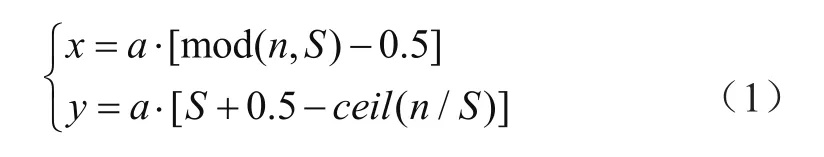
式中：n为需要计算的栅格点；a为单位栅格的长度；x、y为所要计算的栅格的坐标位置。计算出某个栅格点的位置之后，就可以通过基本的距离公式计算出任意2个栅格点之间的距离，其公式为

2 鱼群算法

鱼群算法通过鱼的个体行为和觅食本能进行建模，从而得出一个生物模拟的寻求最优解的方法。首先需要定义鱼群的状态集合X=(x1,x2,…,xn)，在整个集合中的每一个元素，即xi=(i=1,2,…,n)为鱼群中每个参与寻优的个体鱼。该方法的目标函数计算值是对每条鱼所处位置的食物浓度进行考量，则记为Y=f(X)。对于每个鱼个体的定义还有鱼个体的视野范围v、鱼个体所能移动的最大距离s，对于鱼群则有鱼群的聚集程度δ和鱼群的最大试验次数nt，其中2条鱼之间的欧氏距离为|Xj-Xi|，j表示为第j条鱼，i表示为第i条鱼。下面描述鱼的行为。

2.1 觅食行为

某条鱼的位置可描述为Xi，其对应的食物浓度为Yi。依照鱼的视野范围可以搜寻到一个新的位置Xj，并且对应的食物浓度为Yj。那么新位置的计算方式为

式中：v代表鱼个体的视野范围。

当满足新位置所搜寻到的食物状态要比前一个位置的好，即表达式Yi＜Yj，那么在最大实验次数nt范围内，鱼会向新位置前进。计算公式为

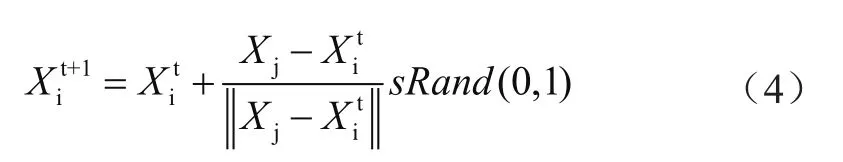
式中：Xit为在时刻t下第i鱼的位置。

如果在实验次数限制的范围中，鱼个体并没有找到比前一个状态更好的状态量，那么鱼会进行随机行为。

2.2 聚群行为

如果聚集中心的状态不满足食物要求和鱼类数量要求，那么鱼群会四散觅食。

2.3 追尾行为

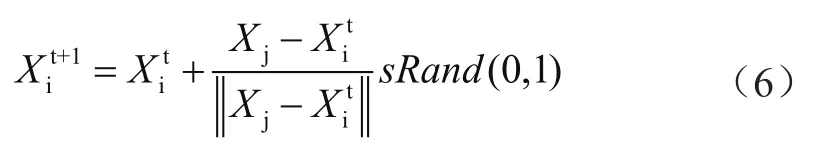
否则，鱼群还是会四散觅食。

2.4 随机行为

随机行为是鱼类最基本的行为，在数学表示上有效避免局部最优，原因在于鱼个体可以广泛寻找同类和食物。随机行为的实现比较简单，就是在视野中随机选择一个状态并向那个方向移动，即

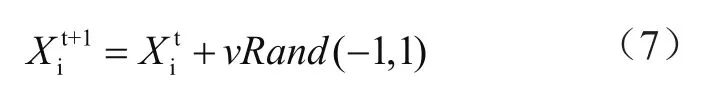
3 实验仿真分析

栅格化之后的地图大小为20 mm×20 mm，依据栅格地图的大小将位置起点设置为(20,1)。放置鱼群大小为N=50，鱼的视野范围为v=20，鱼群的聚集程度设置为δ=0.67，最大实验次数和迭代次数分别为8次和100次。

在该设置下得到的规划路径如图3所示。

图3 规划路径图

本文的鱼群算法能够很好地进行机器人的路径规划，在诸多路径中选取到了最优路线。比较粒子群算法和鱼群算法，算法迭代过程如图4所示。由图4可知，鱼群算法在迭代约30次时，算法趋于稳定，而传统的粒子群算法在迭代进行到约60次才趋于稳定，因此鱼群算法在迭代次数上要优于粒子群算法。

图4 算法迭代比较

4 结 论

通过建立栅格化的变电站图，将机器人路径寻优问题转化为对鱼群觅食模拟和鱼群自身的生物行为，包括聚群行为、追尾行为和随机行为进行最优解的求解。通过比较与粒子群算法，本文的鱼群算法能够很好地进行路径规划，并在求解性能上要优于粒子群算法，有效实现了算法优化。