静止变频器低速阶段转矩改进控制策略

陈 虹，梁 超

(国网江苏省电力有限公司常州供电分公司，江苏 常州 213004)

静止变频器是同步发电机启动和并网的关键设备[1-3]。静止变频器为同步发电机提供频率和功率可控的交流电，从而可以调节同步发电机的转速[4-5]。如发电机异步启动时，会从电网中吸取大量的无功功率，且启动转矩较小，并将产生较大的冲击电流。而变频启动输入较小的电流就能使发电机运行于各种转速下[6-8]，因此变频启动相比于其他启动方式有很多优势。当发电机处于低速运行阶段时，同步发电机反电动势幅值较小，不能为逆变电路晶闸管提供反向电压，不能使用自然换相法，因此工业上普遍采用脉冲换相法实现逆变电路换相[9-10]。

脉冲换相是变频启动的重要环节，关于此阶段问题的研究对于提升系统的稳定性和可靠性具有重要理论意义和工程价值[11]。文献[12]针对转子静止在特定位置时，感应线电压幅值相同，无法根据线电压的幅值大小确定电流型逆变器的初始导通，通过对6种初始导通方案对应的初始启动转矩比较，根据初始启动转矩最大的原则确定了静止变频系统初始导通方案，但是该方案没有考虑转子停在该特定位置之前时失去电磁转矩的情况；文献[13]提出一种基于模型预测控制的静止变频系统脉冲换相阶段控制方法，该控制方法可以使静止变频器输出的电磁转矩跟随参考值，而在换相期间断电的情况下，传统的PI控制方式无法实现这一功能，但该方法需要在有限时域求最优解，求解比较困难且物理意义不明确；文献[14]提出通过控制逆变角γ提高静止变频器的功率因数，从而提高了静止变频器输出的电磁转矩，减小了转矩脉动；文献[15]指出随着转速的上升，负载转矩增加，定子阻抗增加，传统的电流控制方法难以使断续后的电流快速上升并维持稳定。

针对上述静止变频器在低速阶段存在的问题，本文在分析静止变频器输出的电磁转矩的基础上，提出了一种基于双重分区的初始导通方案，该方案有效地提升了驱动同步发电机的初始转矩。同时本文提出整流电路导通角前馈控制和电流闭环控制策略，该策略保证了脉冲换相阶段电流恢复时上升的快速性和持续阶段的稳定性，使脉冲换相阶段转速和回路电流具有良好的动态效果。

1 静止变频器原理及输出转矩分析

同步发电机静止变频系统原理图如图1所示，静止变频系统主电路一般由降压变压器、整流电路、电流型逆变电路、升压变压器和同步发电机组成，网侧和机侧变压器起到改变电压等级和隔离的作用，整流电路将交流电转化为直流电，平波电抗器和逆变电路构成电流型逆变电路，该电路能够将直流电流转化为三相交流电流，平波电抗器具有抑制直流电流脉动的作用。在一个工作周期T内，电流型逆变电路有6种开关组合(T′1，T′2；T′2，T′3；T′3，T′4；T′4，T′5；T′5，T′6；T′6，T′1)，忽略转速的变化，每个开关组合的导通时间为1/6T，在这种工作模式下，电流型逆变电路输出电流产生旋转磁动势，旋转磁动势向量图如图2所示。图中，A、B、C分别为各相电压的矢量位置，FBA、FBC…分别为BA、BC等端口的励磁磁动势。旋转磁动势的频率和幅值与输出电流的频率和幅值相关，旋转的定子磁场与转子磁场相互作用，牵引转子转动，实现同步发电机的变频启动[16]。

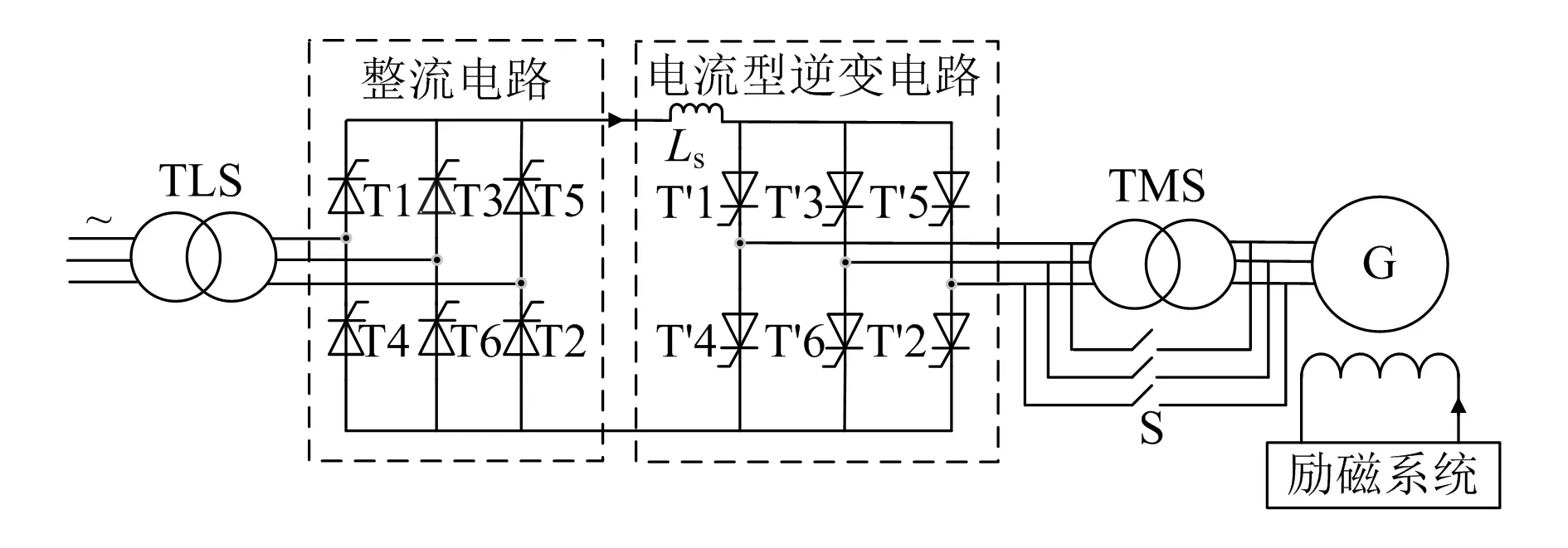
图1 静止变频系统原理图

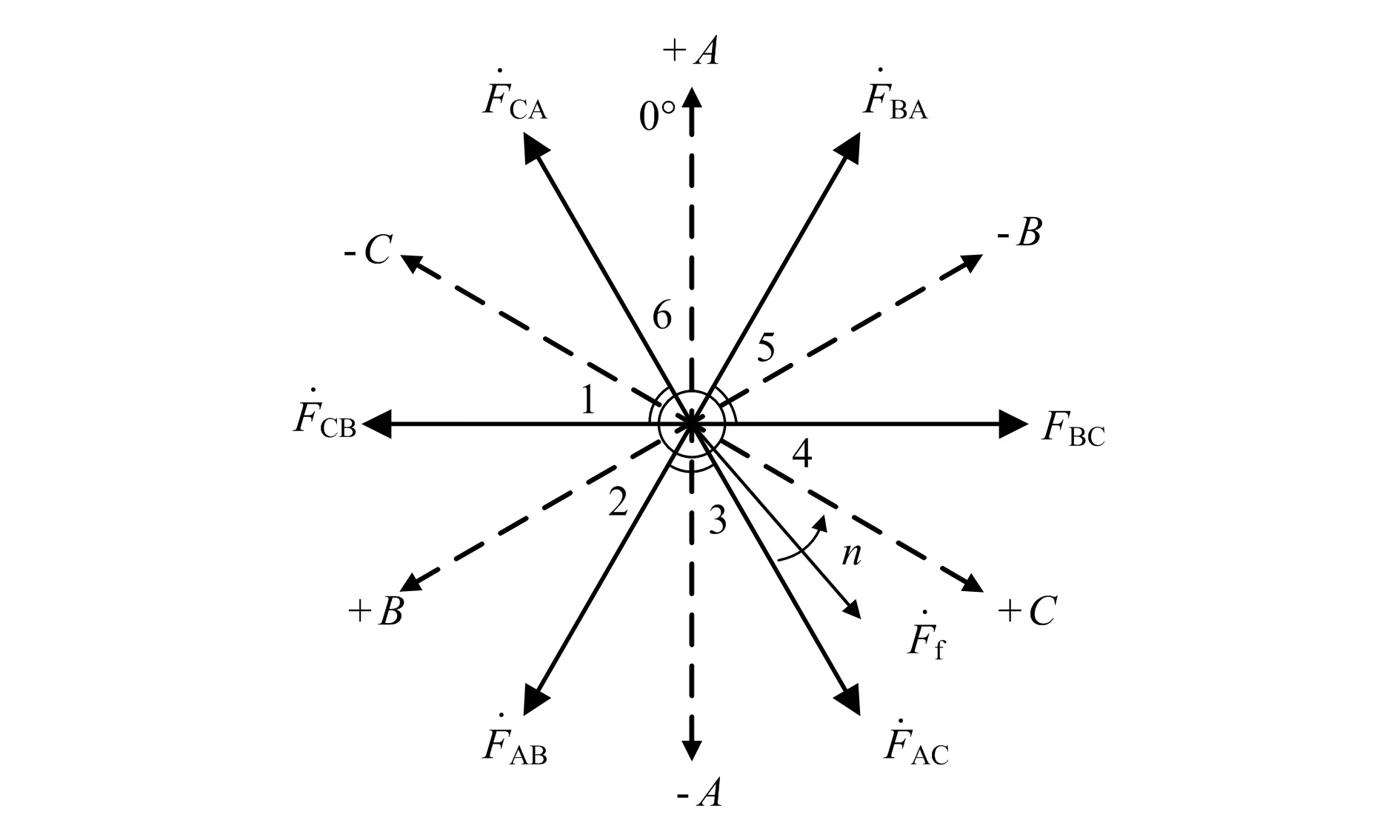
图2 旋转磁动势向量图

静止变频系统的控制系统对整流电路、逆变电路以及励磁系统进行控制，同步发电机在低速阶段和高速阶段运行时，静止变频系统对上述各部分的控制方法不相同。本文研究的低速阶段转矩优化控制策略包括对整流电路的控制和逆变电路的控制，保证励磁系统输出恒定的励磁电流。

下文将通过分析逆变电路驱动同步发电机的电磁转矩，在找出传统逆变电路低速阶段控制策略以及该策略初始导通中的问题的基础上，提出一种基于双重分区的逆变电路的初始导通策略。初始导通后转子具有了初始转速，具备了实现γ=0°脉冲换相条件，从而实现逆变电路最大功率控制。同时通过优化整流电路触发角α，提高直流电流Id的动态性能，提高低速阶段静止变频器的输出转矩。

根据交流发电机电枢反应理论，励磁磁动势Ff与电枢磁动势Fa相互作用产生电磁转矩Te：

Te=KFfFasinθ

(1)

式中：Ff和Fa的单位为A·t；θ为磁动势Ff和Fa的夹角，(°)；K为电磁转矩常数，Wb/A/t。

由式(1)可知，当电枢磁动势超前励磁磁动势90°时，正向电磁转矩最大，根据励磁磁动势的位置，将转子位置平面分为6个扇区，如图2所示。当励磁磁动势进入第1扇区时，应导通T′1，T′6；当励磁磁动势进入第2扇区时，应导通T′1，T′2。以此类推，采用这种导通策略，静止变频器输出的平均电磁转矩最大。

2 静止变频器低速阶段导通角控制策略

2.1 基于双重分区的逆变电路初始导通策略

当转子停在图2中的某分区边缘区域时，由于检测的误差，可能被判别为转子处于上一扇区的末尾区域，而当转子停在上一扇区的末尾区域时，同步发电机在图3所示的t2时间段失去加速转矩，导致同步发电机无法启动，图中，t1=5～8 ms，t2=3～5 ms，t3≈10 ms，t4=10～600 ms。

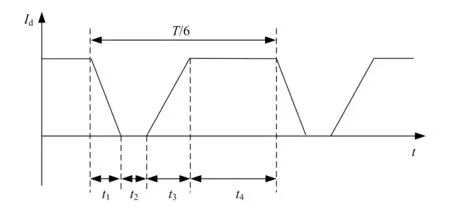
图3 脉冲换相阶段回路电流示意图

针对上述可能出现的情况，本文提出一种基于双重分区的初始导通策略，该策略为：当转子处在两个扇区的交界处时，同时导通能产生正向较大电磁转矩所对应的两组开关组合，如当转子处于扇区6和扇区1交界处时，同时导通T′5，T′6和T′6，T′1两个开关组合，这种初始导通方案能够避免转子在启动后较短的时间内发生脉冲换相，即增加了t4。传统导通区域及改进后的双重分区导通区域示意图如图4所示。改进后导通策略产生的初始转矩Tek0为：

(2)

式中：θ0为传统分区线与转子位置的夹角，(°)。

静止变频器的输出电磁功率Pem为：

Pem=Tek1·ωr

(3)

式中：Tek1为平均电磁转矩，N·m；ωr为电机角频率。

静止变频器在第一次换相时输出的有功功率P为：

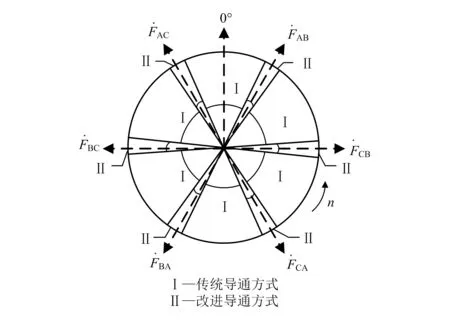
图4 转子位置双重分区示意图

(4)

式中：tk为转子的加速时间，s；t为控制时刻。

2.2 基于导通角前馈控制和电流闭环控制整流电路控制策略

在脉冲换相阶段，静止变频器传统的控制方法一般采用电流单闭环控制，基于电流单闭环控制框图如图5所示，这样的控制策略目的是控制直流电流Id和机端交流电流I的幅值恒定，为同步发电机提供加速转矩。

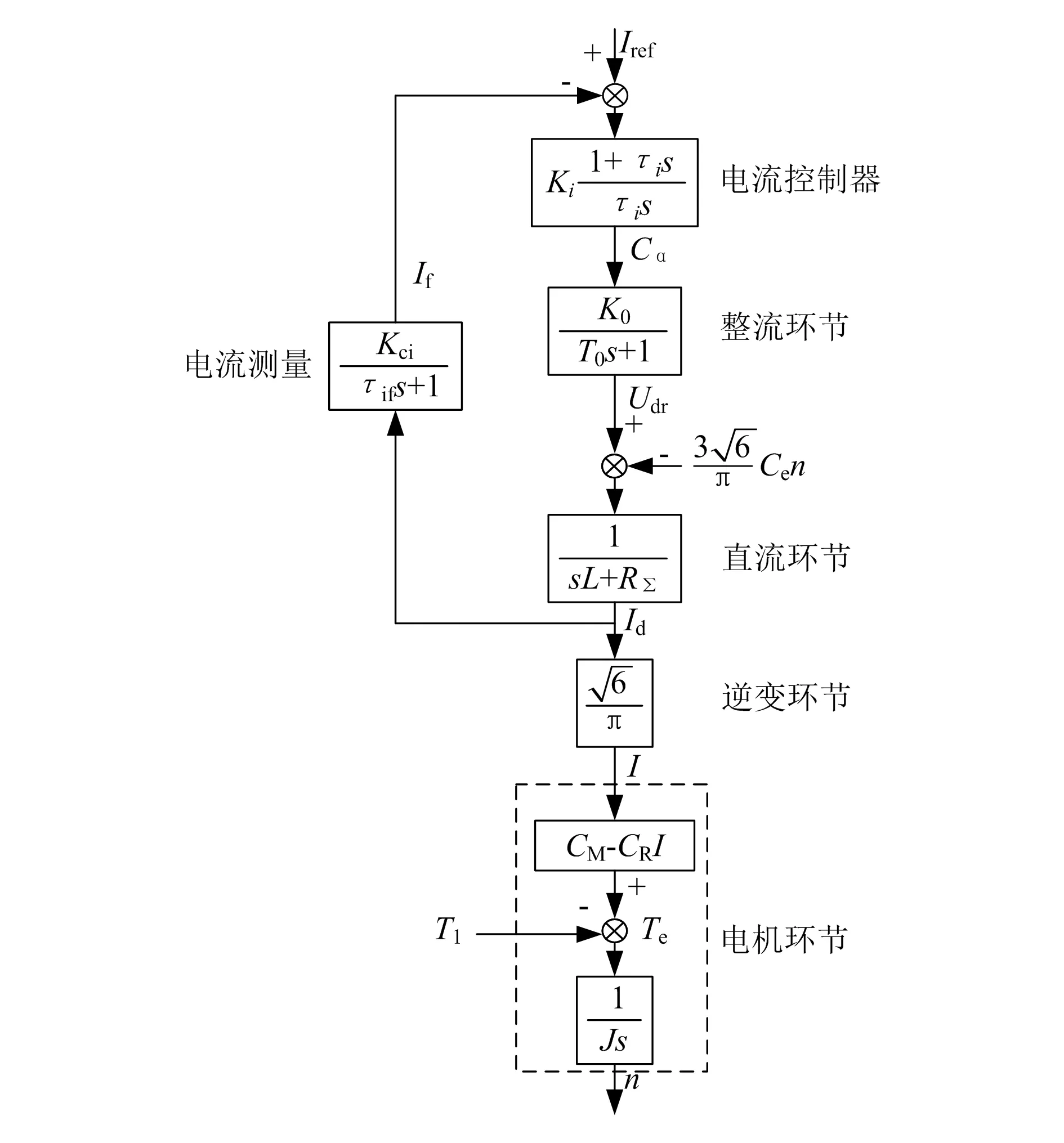
图5 基于电流单闭环控制框图

静止变频器施加给电机的驱动转矩为：

(5)

式中：CM和CR为静止变频系统运行参数；β0为逆变电路空载超前导通角；μi为逆变电路换相重叠角；Ld和Lq为同步电机直轴和交轴同步电感；p为电机极对数。

随着转速的增加，发电机的反电动势增加，其直轴反应电抗和交轴反应电抗也增加，电流单闭环控制整流电路在重新建立直流电流时无法快速上升并跟踪参考值。鉴于此，本文提出一种脉冲换相阶段整流电路控制策略，其包含导通角前馈控制和电流闭环控制两部分。导通角前馈控制转子转速跟随参考值，电流闭环控制采用电流偏差的比例控制。基于导通角前馈控制和电流闭环控制的控制框图如图6所示。

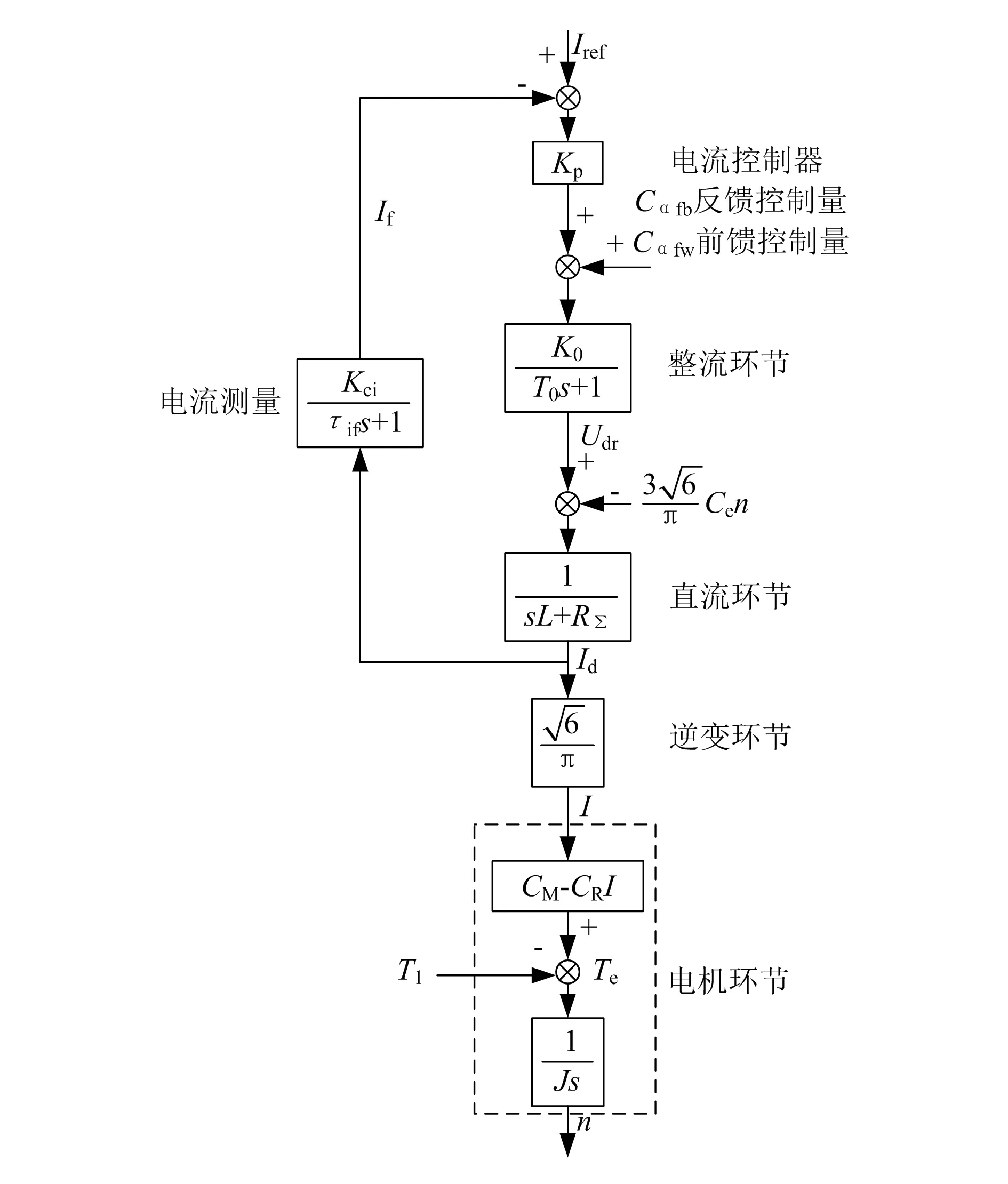
图6 基于导通角前馈控制和电流团环控制的控制框图

电流闭环控制总的表达式如下：

(6)

式中：Cα(t)为导通角指令值；Cαfw(t)为导通角前馈控制量，(°)；Cαfb(t)为反馈控制量，(°)；Cαinit为前馈控制量初始值，(°)；Ki为导通角前馈控制器参数；Δiul为与电流参考值和电流测量值偏差相关的量，A；Kp为反馈比例系数；Δi(t)为电流参考值与电流测量值偏差值，A。

整流电路初始导通角Cαinit对应的直流电流产生的驱动转矩应该大于负载转矩，同时要限制直流电流小于直流电流允许值，即：

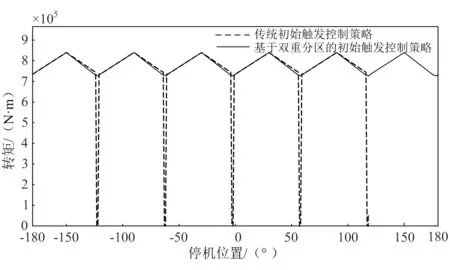
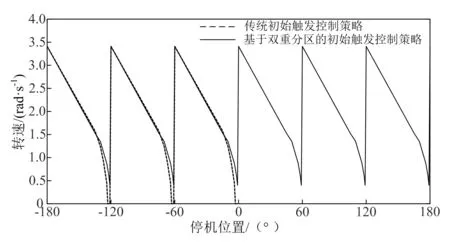
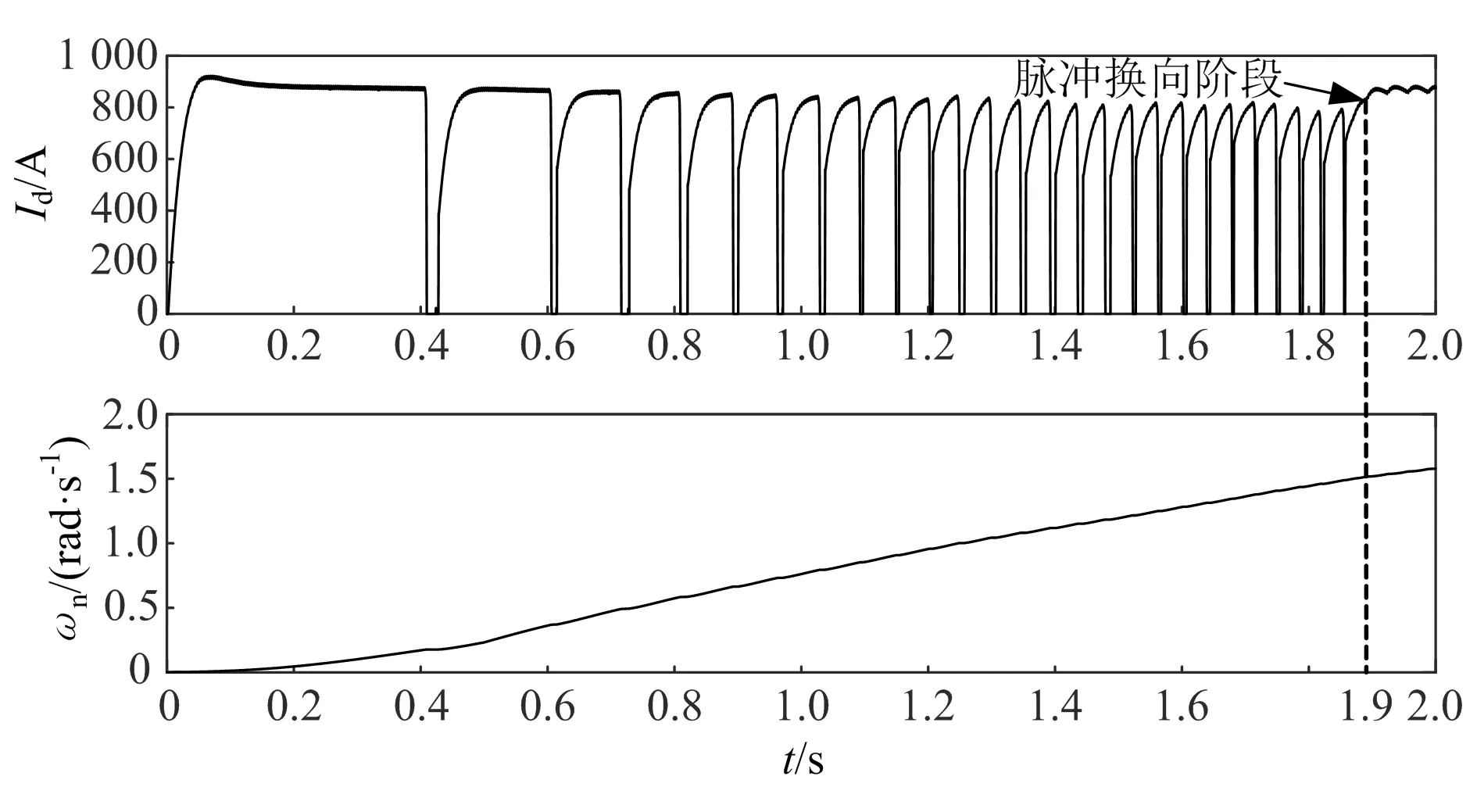
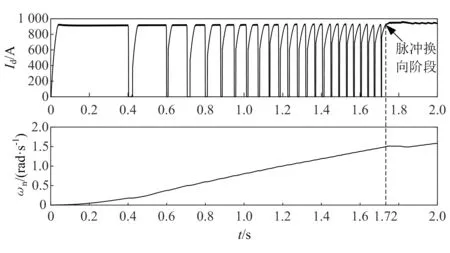
Id.min

(9)

式中：Iinit为初始导通角下对应的电流；Id.min为负载转矩需要的电流；Id.max为直流电流允许值。

t为0.02 s，在0.1～0.2 pu范围内选取合适的电流偏差量Δiul，根据脉冲换相阶段末TD时刻前馈控制量Cαfw(TD)和初始导通角Cαinit确定前馈控制器参数Ki：

Ki=(Cαfw(TD)-Cαinit)·ΔT/(Δiul·TD)

(10)

式中：ΔT为换相阶段的时间差。

根据脉冲换相阶段末TD时刻前馈控制量Cαfw(TD)和直流电流参考值，以及静止变频器整流电路最小控制量Cαmin，确定反馈控制器参数Kp：

Kp·Iref

(11)

式中：Iref为电流指令值。

3 RTDS仿真验证

在RTDS(real time digital simulator)中搭建仿真模型，同步发电机参数见表1，直流电抗器的电感值为40 mH，输入三相电相电压为8 kV，励磁电流在低速阶段恒定为1 000 A，直流电流的参考值为900 A。

表1 同步发电机参数

以停机时转子位置为自变量，初始转矩为因变量，两种初始导通方案的初始转矩比较结果如图7所示，由图7可以看出，初始转矩的变化以60°为周期，以停机转子位置在0°～60°为例，当转子的停机位置在0°～30°时，传统的初始导通方案和基于双重分区的初始导通方案的导通方式相同，因此初始转矩相同，且随着角度的增加，初始转矩逐渐增大；当转子的停机位置在30°～57°时，基于双重分区的初始导通方案的初始转矩比传统导通方案略小；当转子的停机位置在57°～59°时，传统导通方案的初始转矩为零，同步电机不能启动。考虑转子经过初始导通后获得动能，两种初始导通方案的转速比较如图8所示，在50°～59°时，基于双重分区的初始导通方案的转速大于传统初始导通方案的转速。因此，转子的停机位置在0°～49°时应采用传统导通方式，在50°～59°时采用改进导通方式。

图7 两种初始导通方案的初始转矩比较

图8 两种初始导通方案的转速比较

基于电流单闭环控制策略的直流电流和转速如图9所示，从图中可以看出，随着转速的上升，电流的上升时间t3增大，直流电流幅值随着转速的上升而减小，电流在1.9 s后变为连续，静止变频系统切换为高速阶段控制，转子在脉冲换相阶段加速时间为1.9 s。基于导通角前馈和电流闭环控制的直流电流和转速如图10所示，由图可以看出，直流电流基本维持在参考值900 A附近，验证了导通角前馈控制可提高直流电流的稳定性。比较图9和图10可以看出，基于导通角闭环前馈和电流闭环控制的直流电流脉冲间隙，即直流电流为零的时间t2更短，发电机失去驱动转矩的时间缩短，有利于其转速稳定上升。通过比较电流上升到最大值的90%所需时间内电流平均的上升速率可以看出，经过导通角前馈控制和电流闭环控制后电流的上升速率加快，0 s、0.4 s、0.8 s、1.2 s和1.6 s时电流闭环的电流上升速率，传统的控制策略分别为23.38 A/ms、31.28 A/ms、29.07 A/ms、37.10 A/ms、46.25 A/ms，而导通角前馈控制和电流闭环控制策略分别为27.93 A/ms、40.50 A/ms、54.00 A/ms、115.71 A/ms、73.64 A/ms。由于直流电流的快速上升并维持稳定，使得脉冲换相时间缩短为1.72 s。

图9 基于电流单闭环控制策略直流电流和转速

图10 基于导通角前馈和电流闭环控制的直流电流和转速

4 结束语

本文从静止变频系统的原理和输出转矩出发，提出了一种基于双重分区的初始导通方案，该方案保证转子在任何位置都受到正向电磁转矩驱动，且较传统的初始导通方案产生的电磁转矩更大。导通角前馈控制和电流闭环控制换相相结合的控制策略使控制参数更具适应性，实现了脉冲换相阶段电流恢复的快速性并使其维持在一定水平，确保发电机在该阶段升速快速、平稳，进而提高静止变频启动设备的工作可靠性，避免在该阶段发生启动失败。