南海反气旋涡旋温度细结构特征分析

夏 越

(河海大学 海洋学院,江苏 南京 210098)

早期的海洋观测由于仪器的限制,观测资料的垂向间隔很大,在层间深度上的数据必须内插,所得到的海水物理量的垂直剖面被绘制为光滑的曲线,由此逐渐形成了如下观念:在垂直断面上海水的温度和其他物理性质的廓线是平滑变化的。细微结构的观测案例最早可以追溯到19世纪后期的鄂霍茨克海巡航考察[1],不过当时被归结于温度计的故障而被排除。直到20世纪早期,湖泊和海洋中大量增加的温度连续剖面频繁地观测到细结构特征,海洋学家才逐步意识到这一过程。Woods[2]利用染色实验阐明了温度等物理量垂向分布的非光滑性,并提出海洋垂向上存在类似片层结构的理论。随着测量仪器技术的发展,经各种高灵敏度探测仪探测,现已经证实海水的温度、盐度、密度及其垂直梯度的廓线都具有很多精细结构,这些结构在深达3 000 m的深度上都有所发现[3],并被统称为海洋细微结构。

海洋细微结构的存在影响着海洋声速测量结果,研究细微结构有利于水下定位技术的发展;研究形成和破坏海洋细微结构过程中的能量,对估算海洋中能量的转化,包括估计大尺度洋流动能的耗散率都是十分重要的;海洋中低于声频范围的内重力波的传播,也突出了细微结构的效应,内重力波的许多动力学和能量的特征只有根据密度细微层结的存在才可能被理解。因此,研究海洋细微结构是很有意义的。

在海洋学中,“细结构”一词传统上用于描述与分层有关的非均质性,而“微结构”一词常用于描述与小规模湍流有关的非均质性[4]。其中,海洋细结构的概念在不同的文献中的定义有所差别:Munk[5]将海水物理量垂向变化尺度介于1～100 m的脉动称为细结构;Gregg[6]把远大于耗散尺度而小于温跃层的e折厚度的脉动称为细结构;而Eriksen和Curtis[7]和Kunze等[8]将细结构尺度局限在1～10 m;方欣华等[9]结合季节性跃层的厚度尺度,认为以1～10 m的尺度范围作为研究季节性跃层处和浅海海域细结构特性较为合适。

在大洋观测人们发现温盐廓线含有阶梯状的变化,这是扩散对流[10]与盐指现象[11]导致的。关于双扩散的研究可以追溯到19世纪,“热糖指”现象在实验室被发现,然而这种现象当时没有得到重视,“被遗忘了将近100 a”[12]。双扩散现象在海洋中广泛存在,水分的强蒸发会使盐度增大产生盐指[13]、海冰的融化会使冷而淡的水覆盖于暖咸水之上,为对流扩散提供条件,国内外众多学者对北冰洋的双扩散阶梯的研究重点集中在通量计算上[14-17]。地热过程也会导致双扩散阶梯的存在,并且起到了抑制湍流、阻碍垂向热量输送的作用[18]。Orlanski和Bryan[19]提出了大尺度内重力波翻转可能形成阶梯结构的机制。此外,水团分界的锋面通常会形成彼此的侧向侵入,从而在强梯度边界上下都可能产生双扩散现象。Tang等[20]利用高分辨率的海洋人工反射地震观测技术,在赤道附近巴拿马海盆的温跃层底部探测到一个水层界面,他们认为该界面前缘变长/变强的过程对应着该处的湍流扩散正在被双扩散逐步取代的临界过程。

对于涡旋结构的研究,国内外早有开展。Chaigneau等[21]利用卫星与Argo资料,在归一化坐标内合成并得到了涡旋的三维结构。Hu等[22]利用船测资料得到了南海西南部一个冷涡的三维结构,发现其具有倾斜的垂向主轴。Lin等[23]利用海洋模式研究了南海涡旋结构特征,发现涡旋存在3种空间形态。Yang等[24]利用南海18 a海面高度计观测资料,研究了南海中尺度涡旋速度的水平结构,发现涡速结构与涡振幅密切相关。Shu等[25]利用水下滑翔机的高分辨率现场观测数据、海平面异常卫星数据和地转流数据,得到了2015年春季南海北部一个反气旋涡旋的具体结构。

对于细微结构的研究,过去由于仪器性能的限制进展缓慢,国内成果更是非常少,并且以往关于细微结构的研究也局限于个别精度满足要求的数据。例如,蓝昌华和黄华文[26]利用温盐深剖面仪(Conductivity Temperature and Depth,CTD)资料对南海东北部海区上层温盐细微结构进行了初步分析,发现东沙群岛西南的冷涡内部细微结构不明显。本文利用水下滑翔机围绕南海一个暖涡观测得到的3 000多条廓线数据,拟对暖涡细结构的分布特征进行详细地分析。

1 数据来源

温度廓线数据来自于中国科学院沈阳自动化研究所研制的水下滑翔机。水下滑翔机的概念首先由海洋学家Stommel提出[27],它是一种将浮标、潜标技术与水下机器人技术相结合的无外挂推进装置,通过改变自身体积来借助浮力沉降和使用机翼进行水平移动。本文使用的水下滑翔机数据的观测时间跨度为2017-07-14—2017-08-15,地点位于南海某一暖涡(117°～120°E,19°～22°N)附近,最深观测深度约1 000 m,绝大部分廓线垂向分辨率约1 m,共3 000多条,均观测到了明显的温度细结构特征(图1)。

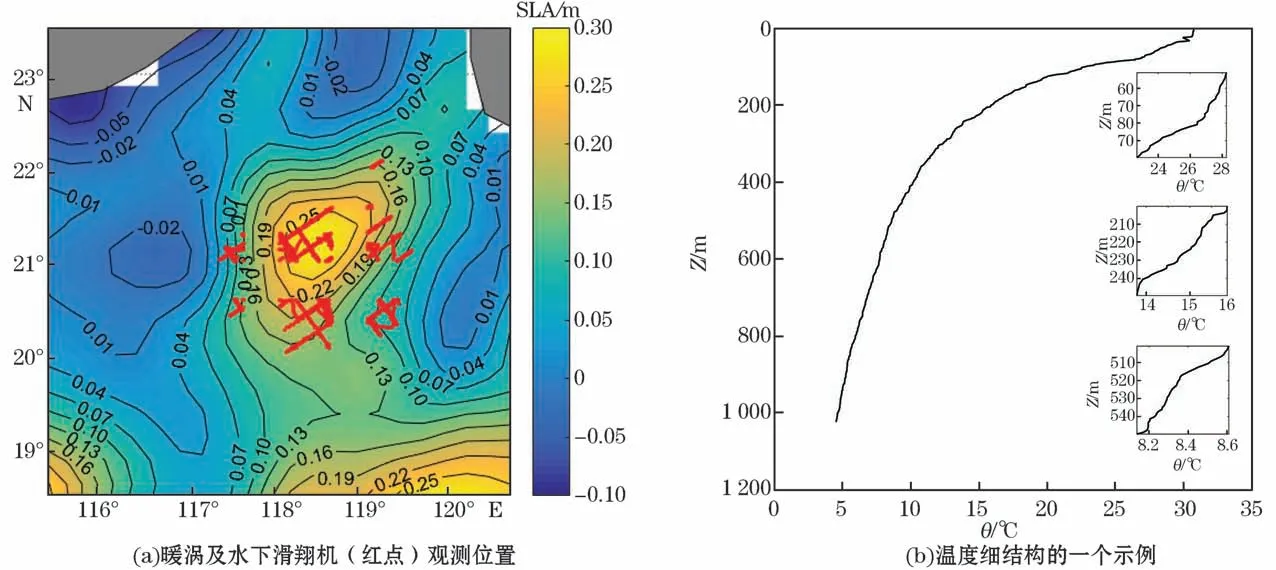
图1 水下滑翔机观测位置及温度细结构示例Fig.1 Location of warm eddy and gliders and observed temperature finestructure

用于识别涡旋的海面高度异常(Sea Level Anomaly,SLA)数据来自法国国家空间研究中心卫星海洋学存档数据中心(Archiving Validation and Interpretion of Satellite Oceanography,AVISO)的卫星高度计资料,由ERS/Envisat,TOPEX/POSEIDON和Jason-1等多颗卫星高度计资料融合而成,空间分辨率为0.25°×0.25°,时间分辨率为1 d。

海表太阳净辐射数据来自ERA5(ECMWF Re-Analysis 5)再分析资料,它是由欧盟资助、欧洲中期天气预报中心(European Centre for Medium Range Weather Forecasts,ECMWF)运营的哥白尼气候变化服务(Copernicus Climate Change Service,C3S)在ERA-Interim的基础上同化了卫星数据、现场观测数据等多种数据产品打造的新一代再分析资料,实现了时空分辨率的大幅提升,空间分辨率为0.25°×0.25°,时间分辨率为1 h。

2 数据处理与分析方法

2.1 廓线分离

为了识别和分析细结构的性质和起源,必须对廓线先进行廓线分离。分离时将温度廓线θ(z)表示为平均值与脉动值和的形式:

式中:z为深度,〈θ(z)〉为温度平均值的垂向分布,θ′(z)为对应的脉动值。式(1)可以由多种取平均的方式实现。由于水下滑翔机缺乏定点持续观测,无法对时间取平均得到平均廓线,海洋近表层由于太阳辐射、风力强迫等原因形成的性质垂向均匀的层被称为混合层,本文针对混合层采用层内取平均、混合层以下采用50 m滑动平均的方式进行廓线分离[26](图2)。

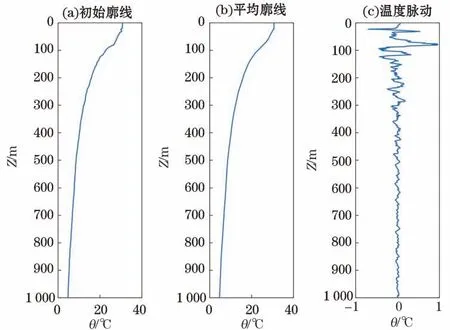
图2 温度廓线分离示例Fig.2 An example of temperature profile separation

2.2 廓线位置归一化

涡旋的识别利用AVISO卫星高度计资料与闭合等值线法[28]。在有水下滑翔机观测的时间段内,由于该暖涡移动速度较大、形状和半径变化较快,水下滑翔机在涡旋内的相对位置需要进行归一化处理:

式中:C为每日涡旋中心;α为以涡旋中心为起点、水下滑翔机某时刻位置为终点的矢量与正东方向的夹角;K为任一条廓线所在的水平位置;P为以C为起点过K做射线与涡旋边缘(最外围闭合等值线)的交点;(dx,dy)为K在归一化圆中的位置。

2.3 涡旋各个方向变形指标

为了探究涡旋变形与细结构的关系,本文定义了一个参数用于衡量涡旋在各个方向的变形情况(图3):每10°均匀取出闭合等值线上的点(即图3中α=10°,20°,…,360°),计算闭合等值线上每个点的外角β,将其作为衡量变形凹凸的依据。

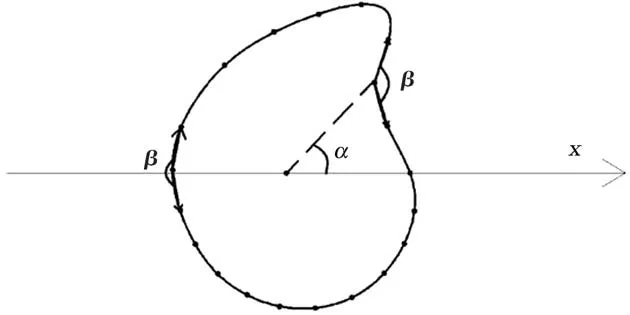
图3 计算涡旋变形指标示意图Fig.3 Schematic diagram for calculating eddy deformation index

当β＞180°时,表示该位置涡旋形状为凸;当β＜180°时,该位置涡旋形状为凹。本文旨在探讨涡旋变形快慢对细结构的影响,将有水下滑翔机观测的33 d内各个方向的凹凸情况算出,同一方向取标准差,用凹凸情况的变化来衡量该方向变形的快慢。

2.4 细结构强度指标

细结构的强度,前人一般采用Cox数来衡量,Cox数首先由Osborn和Cox[29]应用于温度处理,定义如下:

式中的Cθ为Cox数,由于取平均时各自的方法不同,所以不同学者计算得出的Cox数也有较大的差别。方欣华等[9]针对南海的温度Cox数进行研究发现大部分值不超过2且Cox数近似服从对数正态分布。Gregg[30]通过3个不同航次研究得到的Cox发现,不同月份Cox值也大不相同。张爱军和方欣华[31]在赤道附近的断面进行了温盐分析,发现大部分温度Cox数小于1,密度Cox数小于0.5且概率密度分布偏于低值。鲍献文和方欣华[32]认为Cox数的计算存在极大的人为任意性。前人用于计算的数据量虽少但垂向分辨率高于水下滑翔机[8,26],且观测数据的深度较浅,此时采用Cox数来衡量细结构的强度是可行的,但水下滑翔机的测量深度范围大且垂向分辨率低于前人所用资料,经计算Cox数无法表示细结构的绝对强度。因此,本文采用每个点脉动值的绝对值|θ′|作为衡量该点细结构强弱的指标,对于感兴趣的水层采用对脉动绝对值进行深度作积分取平均的方式衡量该水层的细结构强度。

2.5 细结构成因诊断方法

细结构有很多种成因,例如内波、双扩散、湍流混合等[32],本文采用Pingree[33]使用的方法作为诊断判据。为方便解释细结构的选择和统计分析的结果,定义2个参数M和m如下:

可以利用M和m的值判断水层产生的物理过程:

①内波运动学效应情况以及温、盐度垂直混合情况

②等密度平流或等密度混合情况

式(6)～式(9)中:θ′、S′分别为廓线分离出的温度、盐度脉动值;α、β分别为热扩散系数与盐收缩系数;()表示在所感兴趣的水平面邻近的某一深度范围内取平均。与Pingree[33]的计算方法相同,对于每个采样点以100 m范围取平均计算M,m的估计采用,每50 m估计一个m值。与之前廓线分离方法不同的是,这里采用的平均廓线是对所有廓线经过插值取平均得到,而非每条廓线进行滑动平均,本文做定性的讨论,因此可以认为这样的廓线分离是没有问题的。

2.6 其他方法

谱分析是用于研究细结构强弱的重要手段,目前在细结构的垂向谱方面,对于温度细结构的谱特性研究得较多,Levine和Irish[34]得出细结构尺度范围内温度脉动谱斜率为-2.5～-3.0,方欣华等[9]对南海西南海域得出斜率为-3.0～-4.1。方欣华等[35]得出东海细结构的温度梯度谱斜率为-1.0到-1.6。Toole和Hayes[36]分析了赤道潜流区与较高纬度的海流资料,发现垂向谱均在0.1 cpm附近出现明显折断,垂向温度梯度谱可分为3段,以0.1与5.0 cpm为界,当波数大于5 cpm时是微结构区域,会出现最低谱强度。谱方法可以将不同尺度的细结构分离出来,本文将利用温度脉动平均谱研究反气旋涡旋中细结构的特性。

北太平洋次表层水和北太平洋中层水进入南海经混合后会形成高温、高盐的南海次表层水团和低温、低盐的南海中层水团,这样的双层水系统的初始稳定层结不能长久保持,因为分子热传导会使两层之间的温度跃变比盐度跃变消失得快,使得水团界面处的密度分布变成流体静压不稳定,从而发生盐指双扩散现象。表征双扩散强度大小的物理量最先由Turner和Benton[37]提出,他们指出可以由密度率(Rρ)来决定:

式中:Rρ为密度率,α、β分别为热膨胀系数与盐收缩系数,θz和S z分别为温度和盐度的垂向梯度。Ruddick[38]在1983年引入Turner角(Tu)表示双扩散的强度大小:

当Tu位于不同的区间时,其反映的物理意义不同[39]:|Tu|＜45°时,水层处于稳定状态;Tu＞45°时,盐指不稳定产生;Tu＜-45°时,发生对流不稳定。本文采用Tu判定盐指的发生,计算Tu时采用的廓线和计算M、m时一样。

3 涡旋细结构特征

3.1 垂直结构

本文计算出的各个水层的温度细结构强度如图4所示,r为利用2.2节方法计算得到的归一化半径,由温度细结构强度随深度的变化可知,涡旋不同水平位置(0～0.8r、0.8r～1.2r、1.2r～1.6r)细结构强度均呈现自海面向下减弱的特征。这表明自海洋表面向下的物理过程在逐渐减弱。

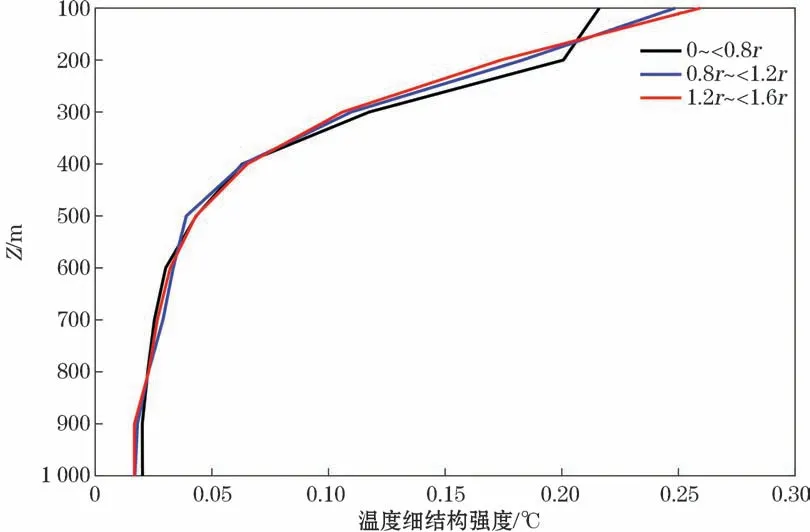
图4 温度细结构强度随深度的变化Fig.4 Vertical variation of temperature finestructure strength

细结构强度随深度的变化与物理过程随深度的变化有关,细结构的成因也会随深度发生变化,初步计算得到了M与m随深度的变化(图5)。

图5 M和m随深度的变化Fig.5 Vertical variation of Mand m

不同深度起主导的物理过程也不相同,图5中M在约120 m与500 m处的间断点为盐度梯度为0所致,在此深度附近不做讨论。在0～100 m,m与M和β/α的值都很接近,海洋表层发生的物理过程受到太阳辐射、风强迫、降雨等多因素的影响,水平与垂向混合过程均占相当比例。而100 m以深对比m与β/α曲线,水平混合不显著,意味着水平混合造成的细结构少。200～300 m深度段m和M几乎相等,表明在这个深度段,垂向混合过程的作用占主导,细结构的成因初步断定主要为垂向过程,如内波、双扩散、跨等密度面混合等。800～1 000 m深度段与200～300 m深度段相似,为垂向混合过程占主导。

为了进一步弄清细结构的成因,本文利用2.6节介绍的方法,计算得到Turner角(图6a)。结果表明,Turner角先随着深度增加而变大,在约250 m处达到最大值,250 m以深随着深度增加逐渐降低,约100～500 m深度段产生盐指,而200～400 m处盐指最为明显。盐指发生的区域,由于盐指引起的热盐输送,该区域的密度通量为净负值,热盐的重新分布通常会产生很多阶梯结构[40],这种阶梯结构也常被认为是发生盐指现象的标志,在本文的观测中温度阶梯结构较为明显(图6b)。结合图5可知200～400 m深度段物理过程主要为盐指造成的垂向扩散,水平方向混合在该水层(以下称为盐指层)很弱。

图6 涡旋区域发生的盐指现象Fig.6 Vertical distribution and variation of salt finger in the eddy region

3.2 水平结构

3.2.1 涡旋内外温度脉动谱的差异

本文涡旋内外温度脉动总体平均谱如图7所示,谱斜率列于表1。

表1 不同深度段、不同半径范围温度脉动平均谱斜率Table 1 Average spectral slope of temperature perturbation at different depth and with different radius range

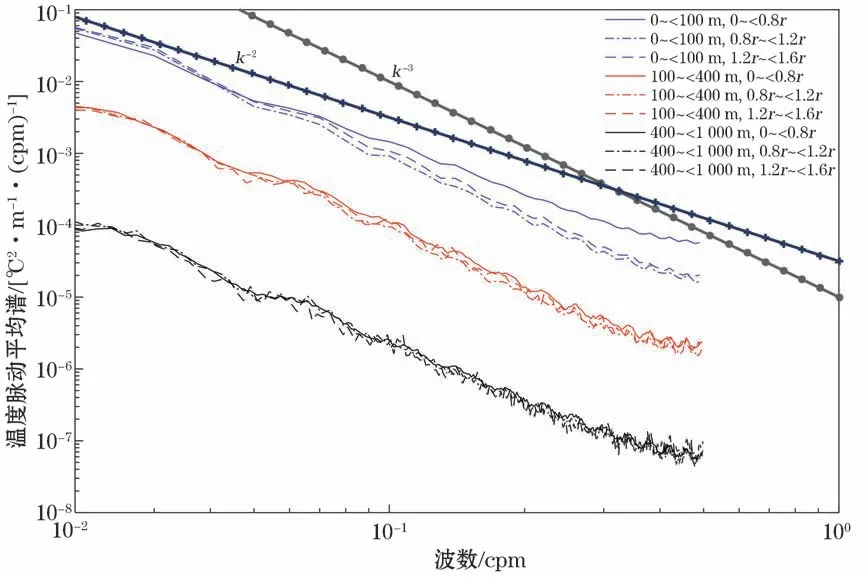
图7 涡旋内部、边缘、外部温度脉动平均谱Fig.7 Average spectrum of temperature perturbation inside,at the edge of and outside the eddy

随着深度的加深,细结构的强度减小,0～100 m深度范围内涡旋内部(0～0.8r)谱斜率为-2.05,而涡旋边缘(0.8r～1.2r)与涡旋外部(1.2r～1.6r)谱斜率分别为-2.48与-2.56,这意味着细结构能量随尺度的衰减在涡旋最大流速内部以内最弱,随着涡旋半径向外延伸,能量随尺度衰减变快,表明0～100 m深度范围内细结构振幅在涡旋外比涡旋内更大。100 m以深不同半径范围温度脉动总体平均谱差异不大。

3.2.2 涡旋变形对细结构的影响

由谱分析结果可知垂向上细结构强度随深度的增加而减弱。为了更直观地展示细结构强度的分布特征,利用每条廓线的位置归一化结果绘制了细结构强度分布特征图(图8)。可以看出0～100 m范围内涡旋细结构强度涡旋边缘向外大于涡旋内部。细结构的谱分析着重体现“振幅”大小的分布,结合图8,这似乎意味着在0～100 m深度范围内,波数小于0.1 cpm的温度细结构在涡旋外部出现得更多。

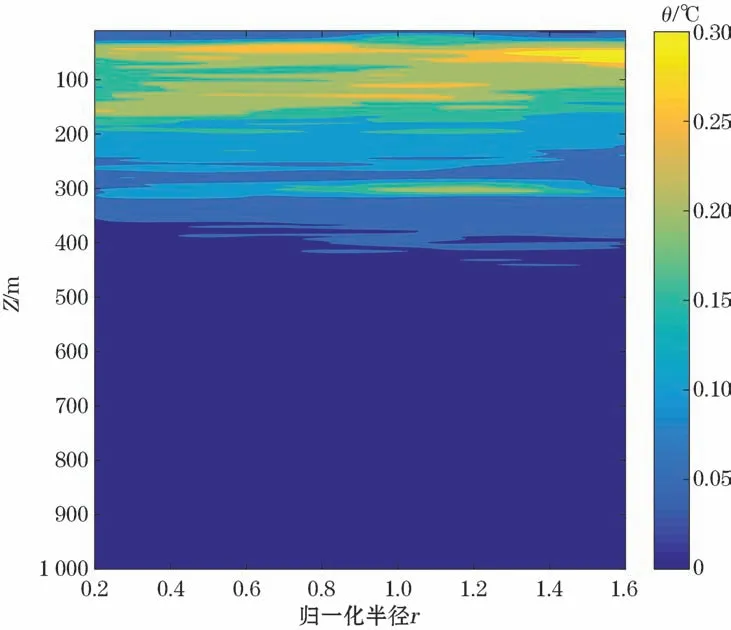
图8 温度细结构强度随归一化半径的分布Fig.8 The vertical distribution of temperature fine structure strength versus normalized radius

本文涡旋变形的计算结果表明:在水下滑翔机观测的33 d内(2017年7月14日至8月15日)各个方向θ的标准差(Standard Deviation,STD)在涡旋东南部(第四象限)最大,即涡旋东南部形状变化最为明显(图9a)。

本文将变形明显涡旋的东南部廓线0～100 m细结构强度的概率密度pdf与变形不明显位置的廓线进行对比(图9b):变形明显涡旋的东南部0～100 m细结构强度概率密度峰右移,从变形不明显的0.20℃右移至0.24℃,形状变化大的区域出现强度大于0.25℃的水层的概率大于外形变化小的区域。这说明0～100 m深度段,涡旋形状变化大的区域细结构比形状稳定的区域细结构更加明显。本文将涡旋海面高度异常中值所在的等值线取出,用于计算涡旋内部的变形情况并与涡旋边缘进行对比(图9a),其中d20为20℃等温线深度,可以指代温跃层深度,自涡旋向外d20逐渐增加。可以看出在各个方向涡旋边缘处的变形情况均比涡旋内部明显。已知0～100 m涡旋变形明显处的细结构强度更大,而涡旋变形自内向外越来越明显,这可以解释图9所展示的0～100 m细结构强度在涡旋边缘向外的区域大于涡旋内部,由于引起涡旋变形的因素过多,具体机制还有待进一步研究。

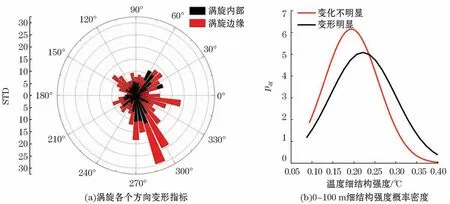
图9 涡旋变形对温度细结构强度的影响Fig.9 Effect of eddy deformation on the strength of temperature fine-structure

为了进一步理解涡旋细结构强度的空间分布,本文依旧将廓线分为涡旋内(0～0.8r)、边缘(0.8r～1.2r)、外部(1.2r～1.6r)三组,通过Turner角得出每条廓线盐指层的厚度。由盐指层厚度的概率分布与盐指层随d20(20℃等温线深度,自涡旋中心向外逐渐减小)的变化结果(图10)可知,由盐指现象从涡旋内向外不断减少。本文认为这可能是因为涡旋外部的流速剪切比内部强,阻碍了盐指的发展[41]。

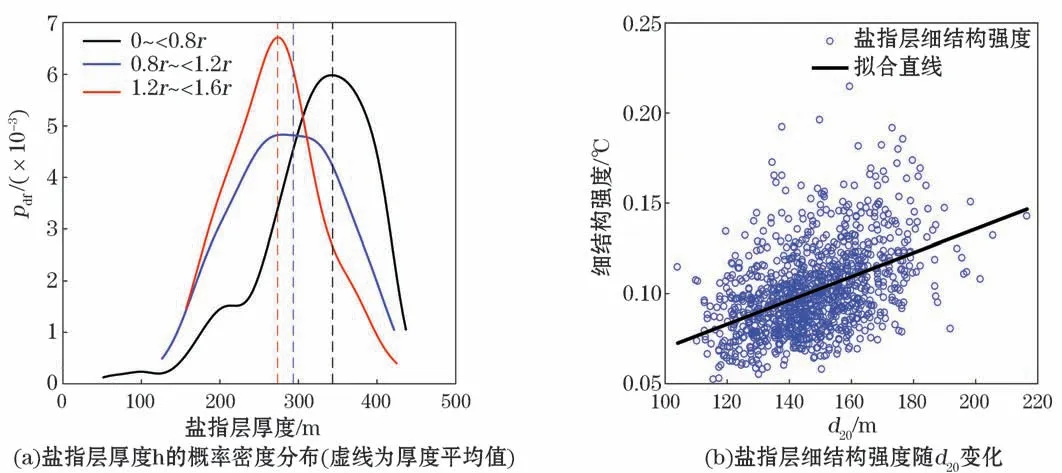
图10 盐指现象在涡旋区域的分布情况Fig.10 Characteristics of salt finger phenomena in eddy region

3.3 细结构的日变化

水下滑翔机在33 d内连续不断的观测使得本文有机会研究涡旋的日变化特征,本文将水下滑翔机数据进行合成得到了涡旋温度随时间的变化曲线(图11),等值线的起伏表明涡旋温度存在较为明显的日变化,细结构强度的日变化特征以及相关影响因素值得探究。

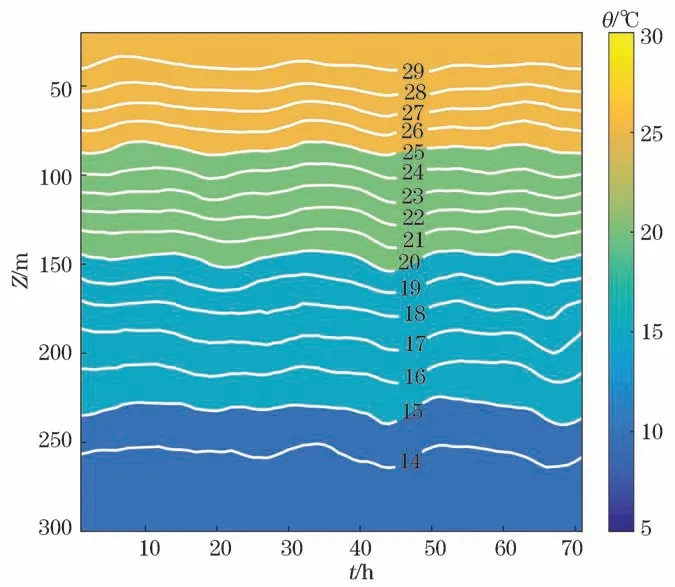
图11 滑翔机观测到的温度的日变化Fig.11 Diurnal variation of temperature observed by gliders

本文将一天时间三等分为00:00-8:00、8:00-16:00、16:00-次日00:00三个时间段,将所有廓线按照观测时间分成3组作脉动平均谱(图12)。谱分析结果表明,0～100 m、08:00-16:00时脉动平均谱振幅与谱斜率均比其他时间段大(表2),这说明该深度范围内08:00-16:00涡旋细结构能量随尺度的衰减比00:00-08:00和16:00-次日00:00慢,进而导致同尺度细结构振幅更大(图12)。本文利用ERA5提供的海表太阳净辐射数据,将涡旋附近的点取出并在水下滑翔机观测的33 d内按照每小时取平均,得到涡旋太阳辐射的日变化(图13),可知08:00-16:00太阳辐射强烈,这可能是谱特性产生变化的原因,而在更深的深度范围内,不同时间段温度脉动平均谱特性相近。

表2 不同深度段、不同时间段温度脉动平均谱斜率Table 2 Average spectral slope of temperature perturbation at different depth and with different time period

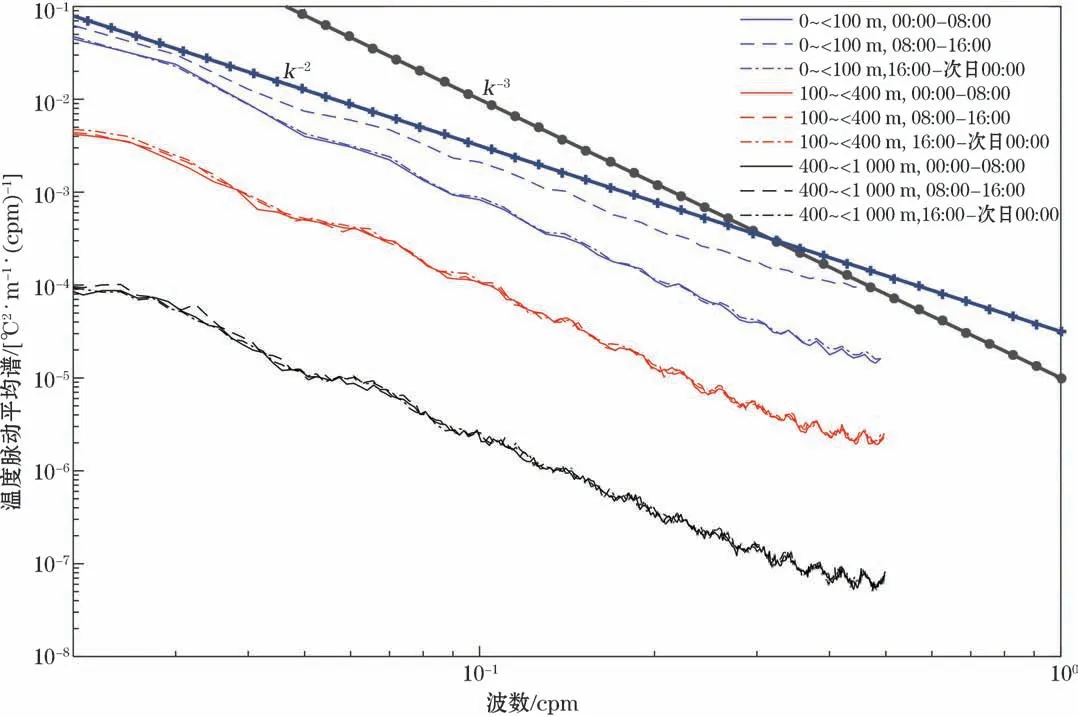
图12 不同时间段温度脉动平均谱Fig.12 Average spectrum of temperature perturbation in different time periods

将廓线按照时间分为3组做谱分析只是为了确定温度细结构日变化的存在性,为了获得其日变化的更多细节,本文将所有廓线按每个小时做了更加细致的分组,对同一时间段的廓线细结构强度做平均,得到了0～100 m与盐指层细结构强度的日变化特征(图14):0～100 m深度范围细结构强度具有周期为1 d的振荡,振幅约0.02℃,细结构强度约05:00至16:00逐渐增强,约16:00至次日05:00逐渐减弱;盐指层细结构强度也具有周期为1 d的变化,振幅约0.008℃,小于表层强度振幅,细结构强度前半天减弱而后半天增强。盐指层以下细结构强度的日变化不明显,本文不做讨论。

将图13和图14对比,发现0～100 m细结构强度在有太阳辐射的时间段增强,在没有太阳辐射的时间段减弱。似乎在白天太阳辐射最强烈的时段,细结构更加明显,也容易得到保持。我们猜测可能是由于海洋表层夜间发展的对流在一定程度上削弱了垂向细结构,而对流在白天由于太阳辐射遭到了抑制,所以白天更有利于细结构的发展,这样的差别也被直接反映在脉动谱的振幅与斜率上(图12)。对于盐指层,本文发现细结构强度的日变化与d20的日变化十分相似(图15):当d20减小(变大)时,盐指层细结构强度减弱(增强),这表明盐指层细结构强度的日变化与温跃层深度的变化有着密切的联系,但具体机制仍有待研究。

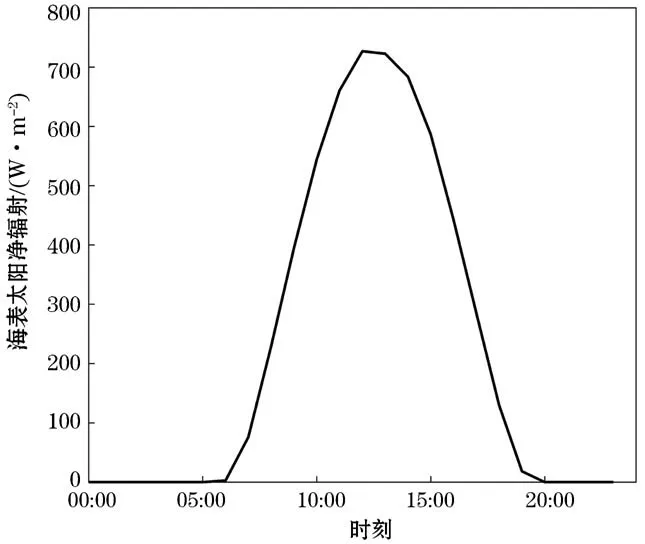
图13 涡旋范围内太阳净辐射的日变化Fig.13 Diurnal variation of the net solar radiation within the eddy

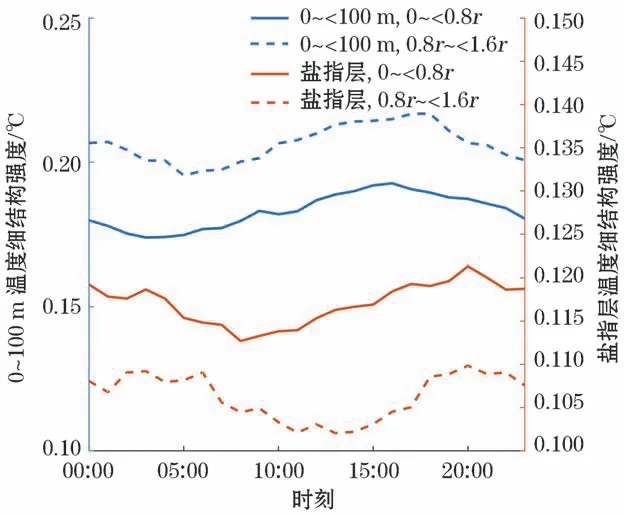
图14 0～100 m与盐指层温度细结构强度的日变化Fig.14 Diurnal variation of temperature finestructure strength in the depth range of 0-100 m and salt finger layer

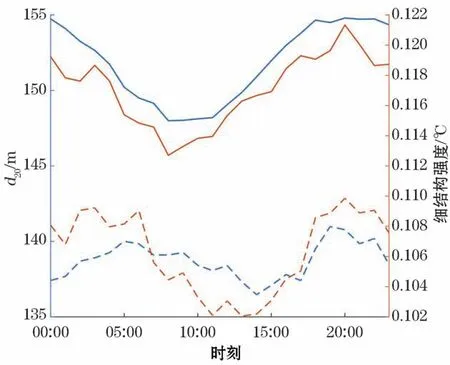
图15 盐指层细结构强度的日变化Fig.15 Diurnal variation of d20 and finestructure strength of salt finger layer

4 结 语

海洋细微结构是很多不同的物理过程共同作用的产物,同时又是海洋物质输运和能量平衡上一个极重要的环节。细微结构的存在影响着海水中物质、能量、动量的传输以及能量的耗散,研究细结构有助于估算海洋中能量的转化。本文利用围绕南海某一涡旋进行测量的水下滑翔机观测的3 000多条廓线,通过对每条廓线按半径比例做归一化处理,定义水层细结构强度的指标,分析了温度细结构在涡旋中的分布特征,得到的结论如下:

1)在垂向上,细结构的强度从海洋表层至深层呈现上大下小的特征,海洋表层水平与垂向过程共同作用产生细结构,在约100～400 m深度范围盐指较为活跃,产生了阶梯状温度细结构。

2)在水平方向上,在0～100 m海洋表层,细结构能量在涡旋最大流速所在半径内部衰减最弱,随着涡旋半径向外延伸,能量随尺度衰减变快。涡旋内部变形小于涡旋外部,导致细结构强度自涡旋向外逐渐增强。在100～400 m深度范围内,盐指层厚度在涡旋内部更大,该层细结构强度呈现涡旋内部大于涡旋外部的特征。

3)在时间变化上,0～100 m海洋表层白天温度脉动平均谱的振幅和斜率均比其余时间大,且细结构强度随着太阳辐射的增强而增强,原因可能是夜间发展的对流混合削弱了垂向细结构,而该对流在白天由于太阳辐射受到了抑制。在盐指层细结构强度的日变化特征与温跃层深度的变化有关。

随着观测资料分辨率的提升,针对细微结构的研究已成为了可能。本文对涡旋温度细结构的研究是依据多组水下滑翔机数据进行的,通过分析大量垂向分辨率相对较高的廓线得到了一些成果,但也有不足之处:由于缺乏定点时间序列观测数据,关于内波对细结构的影响以及细结构寿命长短的研究无法进行;缺乏海流实测资料与观测到的细结构进行对比,且垂向分辨率为1 m的资料无法用来研究微结构,而具有高分辨率(0.1 m)的温盐测量仪器目前很难像水下滑翔机那样可以在短期内观测得到大量数据。相信随着水下滑翔机垂向分辨率的提高,关于涡旋细微结构的深入研究能够顺利进行,弥补目前的数据短缺现象。