基于混沌自适应萤火虫算法的UAVs分配策略

宋阿妮 包贤哲 权 轶

(湖北工业大学电气与电子工程学院 湖北 武汉 430068)

0 引 言

无人机(Unmanned Aerial Vehicle，UAV)以其快速、精准、低风险等优势已经广泛应用于军事[1]、农业[2]、运输等领域[3-6]。战场无人机作为新型作战装备在现代战争中起着不可代替的重要作用，在武装打击、敌情侦察、目标追踪、山地搜索、危机预警、定点监视等多种类任务方面能够很好地代替人力，大幅度降低执行任务风险并克服复杂地形障碍[7]。但随着无人机数量激增，任务数量和复杂度不断上升，寻常算法的分配运算时间大幅增加，无法满足现代战争对作战任务快速分配响应的要求。所以如何在战场任务数量和无人机基数较大的情况下合理分配任务获得最高收益是当下无人机作战任务分配研究热点。很多学者尝试引入各类智能优化算法来解决此类问题[8]。其中萤火虫优化算法以其易于实现、优化性能好、限制条件少等优点，成为目前运用较为广泛且应用效果最好的方法[9]。

在萤火虫算法研究中，Wang等[10]提出了一种随机吸引的萤火虫算法模型。该算法通过随机选择一个亮度更高的个体进行移动从而减少收敛时间和复杂度，但由于移动次数过少容易引起算法早熟。Zhou等[11]引入了概率参数p来控制萤火虫的吸引频率，此方法被称为部分吸引模型。只有在个体亮度高于本体且概率参数同时满足要求时才能移动，此方法有效地加快了收敛速度，但概率参数p的选定却是一个难题。Wang等[12]提出了邻域吸引模型，本体与一定范围领域内的个体进行比较，通过控制领域的大小，可以有效控制算法收敛速度，但个体周围领域大小过于依赖问题特征。随着算法研究的不断深入，传统萤火虫算法存在着容易陷入局部最优解和随机移动造成的收敛速度过慢收敛精度不高的问题。

本文将传统萤火虫算法的移动步长改进为自适应步长，在位置更新信息中加入全局历史最优值和自适应惯性权重，采用变尺度混沌方法改进光吸收强度系数，提出混沌自适应萤火虫算法(Chaotic adaptive Firefly Algorithm,CAFA)，并应用于多作战无人机多任务分配问题。该算法有利于更精确地找到最优分配方案，提高系统的响应速度和机动性。

1 问题分析与模型建立

设定无人机作战任务分配问题中，敌我双方在交战地域S=[0,s]×[0,s]内，有n个不同类型任务M=(M1,M2,…,Mn)等待无人机执行，需要从无人机基地派出Q架无人机完成交战地域S内的所有任务。为了躲避敌人雷达和监控设备对无人机的探测减小其坠毁概率，设立圆形禁飞区Ρ，无人机禁止在此区域内飞行，其实时位置(xVi,yVi)∉P。上述无人机的任务分配调度问题可定义为一个优化模型：一组无人机V={V1,V2,…,Vm}，一组待完成的任务M={M1,M2,…,Mn}，将任务风险指数、航程代价指数作为系统成本，任务完成潜力指数和执行任务价值指数作为系统收益，通过模型评价指标以评价当前分配方案的优劣，最终确定最佳分配方案。

1.1 任务风险指数

任务风险指数是指无人机在执行任务时损毁的概率大小，设无人机Vi号执行Mj号任务时的任务风险指数为：

(1)

式中：ValVi为无人机Vi号的价格成本；ThrMj为无人机完成任务Mj号发生损毁的概率大小；max{ValVi|1≤i≤m}是所有无人机中的最大价格成本。

1.2 航程损耗指数

任务航程损耗指数是指无人机完成任务时间长短，设无人机Vi号执行任务Mj的航程损耗指数为：

(2)

式中：DisVij表示无人机Vi与任务Mj之间的距离；max{DisVij|1≤i≤m}表示所有无人机到任务Mj的最大距离。

1.3 任务完成潜力指数

任务完成潜力是指无人机完成指定任务的概率大小，应优先分配任务给完成概率大的无人机。设无人机Vi号完成任务Mj的潜力指数为:

(3)

式中：TiVi表示无人机Vi号在空中飞行的最大时间；max{TiVi|1≤i≤m}表示所有无人机在空中飞行的最大时间；Potij表示无人机Vi号执行任务Mj时的任务完成概率。

1.4 执行任务价值指数

执行任务价值指数是指无人机在完成匹配任务后能够创造的最大价值，设无人机Vi完成匹配任务Mj的执行任务价值指数为:

(4)

式中：ValMj表示完成任务Mj的收益；max{ValMj|1≤i≤m}则表示所有任务中完成收益最大值。

1.5 战场无人机禁飞区域

在现代战争中，雷达等侦测手段成为了无人机的头号敌人，躲避雷达和监控设备将会大大降低无人机坠毁概率，为了模拟敌人的雷达和监控设备，无人机在完成任务过程中禁止在该区域内飞行，即满足：

(5)

式中：Vxi、Vyi分别表示无人机飞行状态下的横纵坐标；Oxi、Pyi则表示敌军雷达和监控设备的横纵坐标。

考虑应以最短时间执行任务，无人机执行任务路径为直线往返，所以无人机与禁飞区中心位置最短距离大于等于其安全半径可转化为无人机与被执行任务之间连线与禁飞区圆形区域相切或相离，过禁飞区圆心向无人机飞行路径直线作垂线，无人机到禁飞区边缘的最近距离：

(6)

式中：Aijx+Bijy+Cij=0为无人机Vi执行任务Mj时无人机位置与任务点位置连线的直线方程；Ri(i=1，2，…,n)为禁飞区的安全半径。

1.6 无人机分配优化模型

任务风险指数以及航程损耗指数作为代价指标需要进行最小优化，而任务完成潜力指数和任务收益指数作为最终收益要进行最大优化。为了能够将优化目标统一，采用倒数方法表示系统任务收益。

(7)

式中：Get_Fin为完成任务潜力指数的倒数；Get_Inc为执行任务价值指数的倒数。

将四个指标的线性组合作为无人机分配任务的综合评价指标来评判分配方案的优劣，由此得到最终的无人机分配优化目标函数为：

(8)

式中：m和n分别表示无人机和任务的最大数量。m和n的约束条件为：

(9)

式中：kVi为每种类型无人机的最大任务负荷，无人机执行任务数量不能超过其最大任务负荷；hij表示无人机Vi号是否去执行了任务Mj，记录无人机完成任务的状态，若无人机Vi完成了任务Mj则将其各项指标代入计算，否则不列入数值。计算表达式为：

(10)

2 多无人机分配优化算法

2.1 经典萤火虫算法

经典萤火虫算法是一种启发式算法，灵感来源于萤火虫闪烁行为。萤火虫不分性别，任意个体将会吸引到所有其他的萤火虫。吸引力与它们的亮度成正比，对于任意两个萤火虫，亮度低的萤火虫被吸引，向更加明亮的移动，其亮度又随着其距离的变化而变化。如果在某个萤火虫邻域范围内没有亮度更高的萤火虫，那么它会随机移动，直到集中于全局最亮萤火虫的周围。

群体中每一个萤火虫都对应问题的一个可能解。假设Xi=(xi1,xi2,…,xid)是一只萤火虫，其中：i表示萤火虫的编号；d表示每一个萤火虫解的纬度数。对于两只不同的萤火虫即不同解Xi、Xj,i≠j，二者之间的吸引度可以表示为：

(11)

式中：β0表示距离r=0处的吸引力；rij表示两只萤火虫之间的距离；γ表示两者之间传播媒介对光的吸收率，由介质性质决定。式(12)即为两只不同萤火虫之间的距离。

(12)

移动公式表示为：

xid(t+1)=xid(t)+β(rij)·(xjd(t)-xid(t))+αε

(13)

式中：α∈[0,1]表示萤火虫每次移动的步长的系数；ε为常数，表示移动步长；t表示迭代的次数。所有萤火虫按照式(13)向着更优个体移动。

2.2 改进的混沌自适应萤火虫算法

萤火虫算法容易陷入局部最优解，而且还存在着最亮个体距离过远而导致的萤火虫无法集中收敛和收敛速度慢问题。对传统萤火虫算法进行改进，运用变尺度混沌方法将光吸收系数改进为跟随迭代次数不断更替的混沌数值，再将萤火虫的位置公式中引入全局最优以及自适应步长因子与惯性权重来整体优化萤火虫算法的性能。

2.2.1步长因子优化

理想情况下，萤火虫最终会收敛于极少点或者单个点，由此可得到：

(14)

当迭代次数达到一定数值时，式(14)就会收敛为一个数值，收敛后的解不再发生变化，此时可以根据式(11)-式(13)得到：

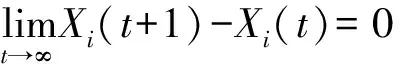
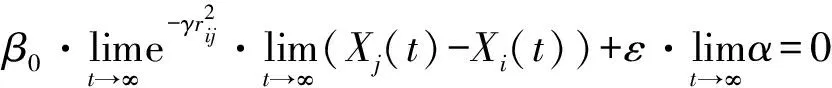
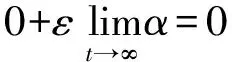
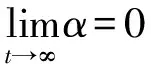
(15)

由式(15)可知，当最终结果收敛时，步长因子α=0。

根据此性质，提出一种自适应步长的改进方案：

(16)

式中：Tmax为迭代最大次数。

由式(16)可以看出，当迭代次数增加时，步长因子在不断减小，在t→∞时步长因子α→0，加快了收敛速度和精度。

2.2.2自适应惯性权重

为了能够使得萤火虫移动时方向和搜索距离更加准确，在萤火虫上一时刻位置xid(t)前引入μ(t)自适应惯性权重：

(17)

式中：gbest(t)为萤火中历史全局最优值；E(f)为第t次迭代所有目标位置的平均值：

(18)

通过引入自适应惯性权重，使得计算后期萤火虫的收敛精度和速度进一步提高。

2.2.3引入历史全局最优值

在萤火虫的位置更新中加入历史全局最佳位置，让萤火虫有记忆地搜寻最优解，在向更亮的个体移动的过程中同时向着历史最佳位置靠拢，使得位置较远的萤火虫也能在迭代次数较高的情况下集中于全局最优解附近，大大加快了收敛速度和收敛精度。改进后的位置公式为：

xid(t+1)=μ(t)xid(t)+β0(rij)·(xjd(t)-xid(t))+

ω(gbest(t)-xid(t))+α(t)ε

(19)

式中：gbest(t)是迭代次数为t时的历史最佳位置。ω系数随着t增大而减小：

(20)

2.2.4变尺度混沌光强度吸收系数

光吸收系数γ是影响萤火虫搜索精度和速度非常重要的参数[13]，能够很大程度影响到萤火虫向最优解集中。当γ→∞时，根据式(11)可知β(i,j)→0，萤火虫的吸引力最小，有利于在小范围内细化搜索；当γ→0时，β(i,j)→∞，萤火虫吸引力最大，可以进行大范围移动，有利于在大范围内全局搜索最优解。如果光吸收系数设定为常数则会影响到萤火虫搜索的精度和速度，基于此提出一种变尺度混沌光强度吸收系数来强化萤火虫的全局与局部搜索能力。

混沌是一种普遍存在的非线性现象，具有随机性、初值敏感性、应用便利性，利用这些特性改变萤火虫的光吸收强度系数，让算法能够跳出局部最优解，避免了迭代过程中光吸收强度保持不变的缺陷。

根据Gandomi等[14]对映射函数的分析，选择混沌应用效果较好的Sinusoidal映射，其公式为：

(21)

式中：a为一个幅值常数。

搜索空间对于混沌优化方法有较大的影响，搜索空间较小时效果较为明显，搜索空间过大会导致混沌优化失效。随着搜索空间的增大，搜索精度也会进一步降低，所以采用变尺度混沌方法限制其搜索空间大小。将式(21)改进为：

(22)

式中：

(23)

此时光强度吸收系数为：

(24)

萤火虫的亮度公式改进为：

(25)

βrev(i,j)随着迭代次数变化的曲线如图1所示，迭代前期收敛速度较快，能够提高收敛速度，迭代后期搜索范围变小，收敛速度较慢，有利于群体在小范围内精确寻找最优位置。

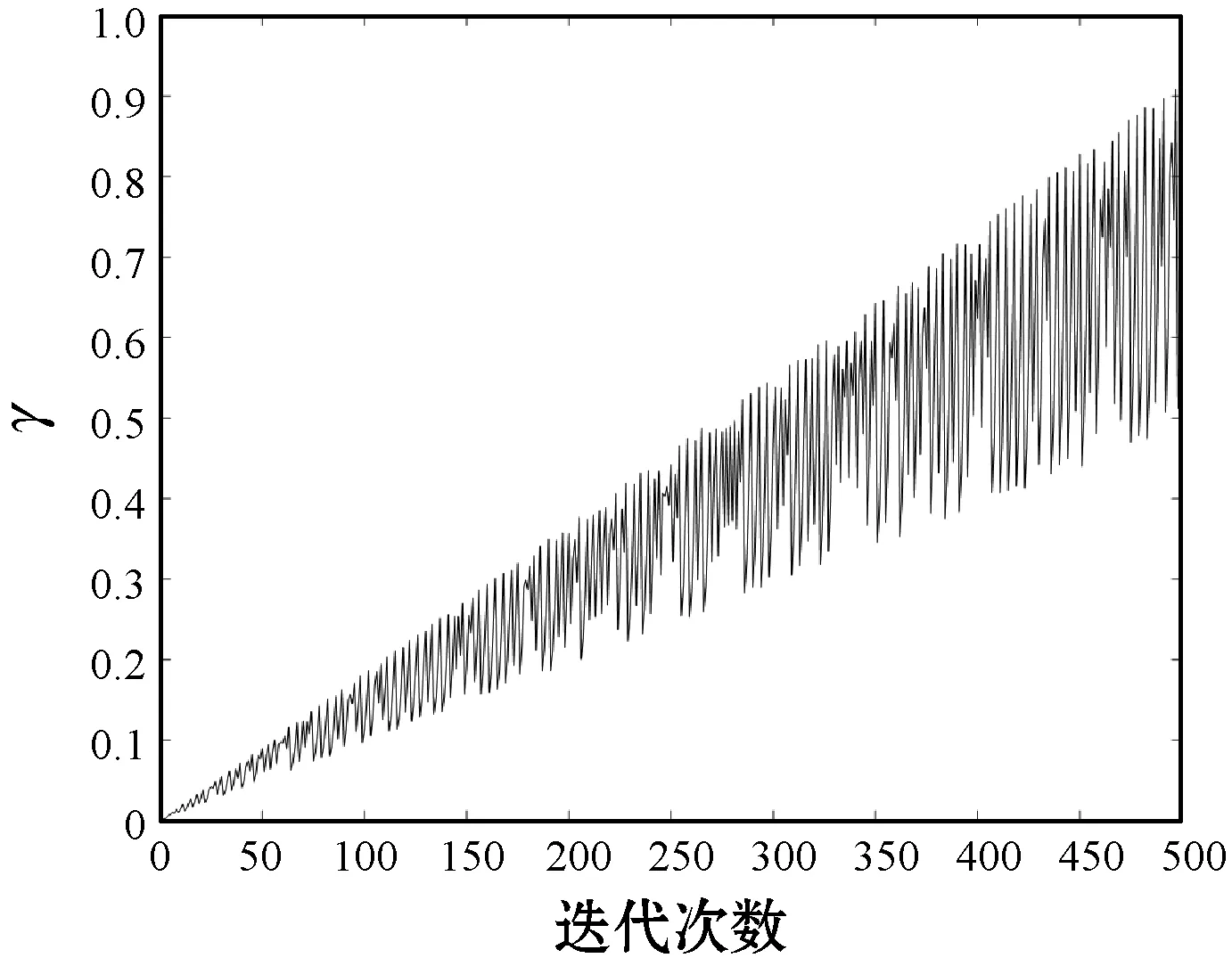
图1 混沌变异γ变化曲线

根据上述提出的改进方案，变尺度混沌自适应萤火虫算法(CAFA)的流程如图2所示。

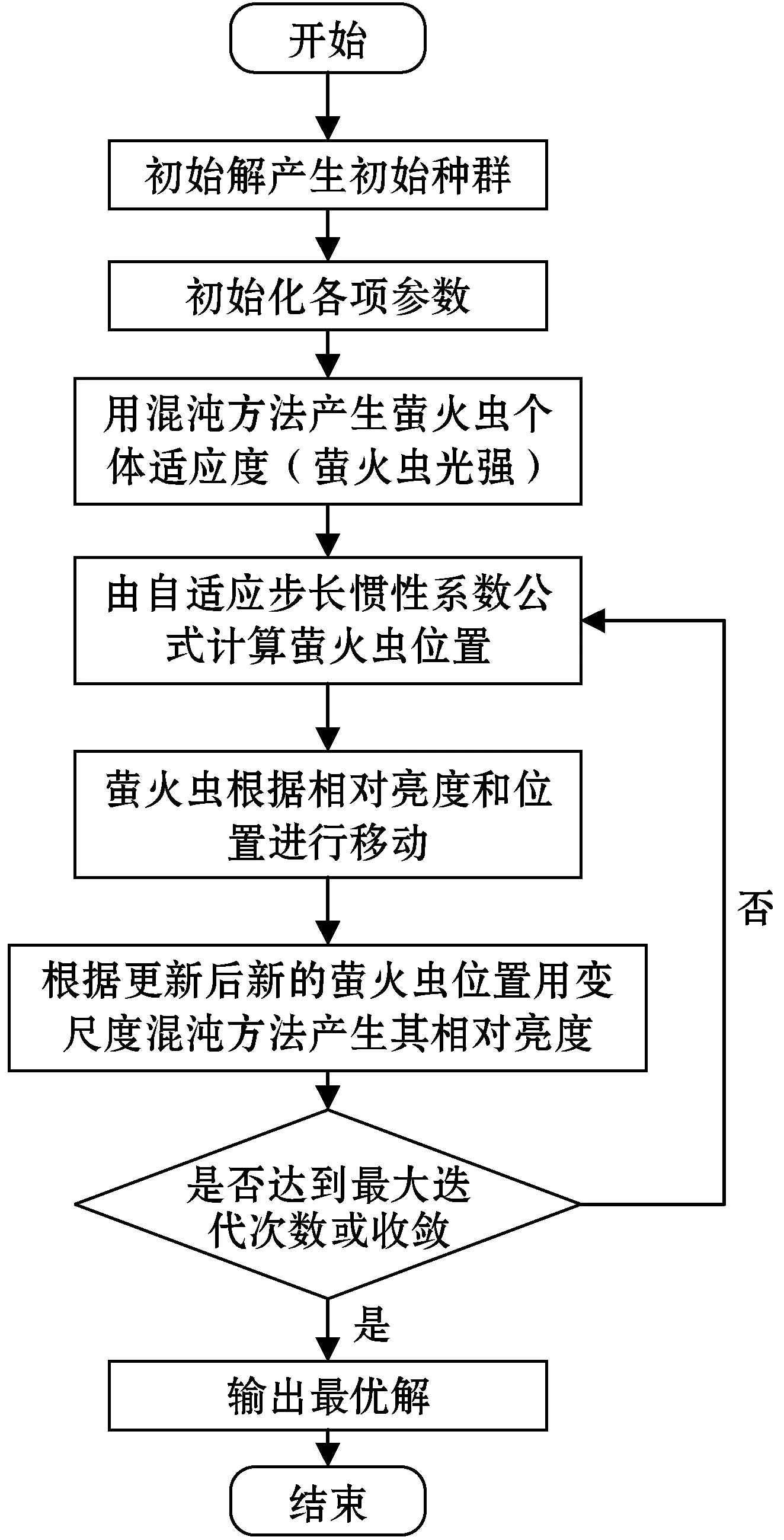
图2 混沌自适应萤火虫算法流程

3 实验与结果分析

为了验证提出的分配算法的合理性，本文设计了如下算例进行无人机协同作战仿真实验。假设任务开始前，我军已经获取了敌军所有目标部队以及交战区域敌军防空阵地的坐标，敌我双方交战的地域S=[0，80]×[0，80] km2内，有15个地点安排有不同类型任务，并且4架作战无人机已被我方地面部队送达适合起飞的4个位置执行相关任务。作战地域整体分布情况如图3所示。

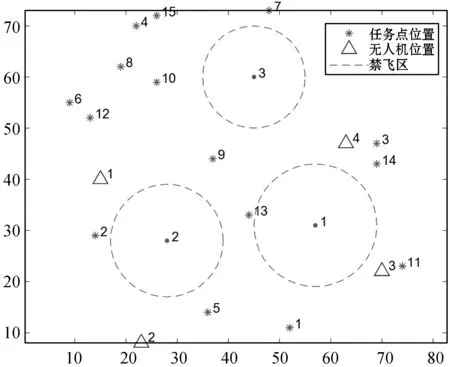
图3 作战区域整体位置分布

在交战区域S内设立三个禁飞区，无人机在完成任务过程中禁止在该区域内飞行即满足：

(26)

式中：Vxi、Vyi分别表示无人机飞行状态下的横纵坐标；三个雷达的侦测范围分别为方圆12 km、11 km、10 km。

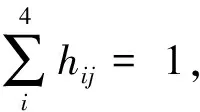
表1 无人机各项参数表

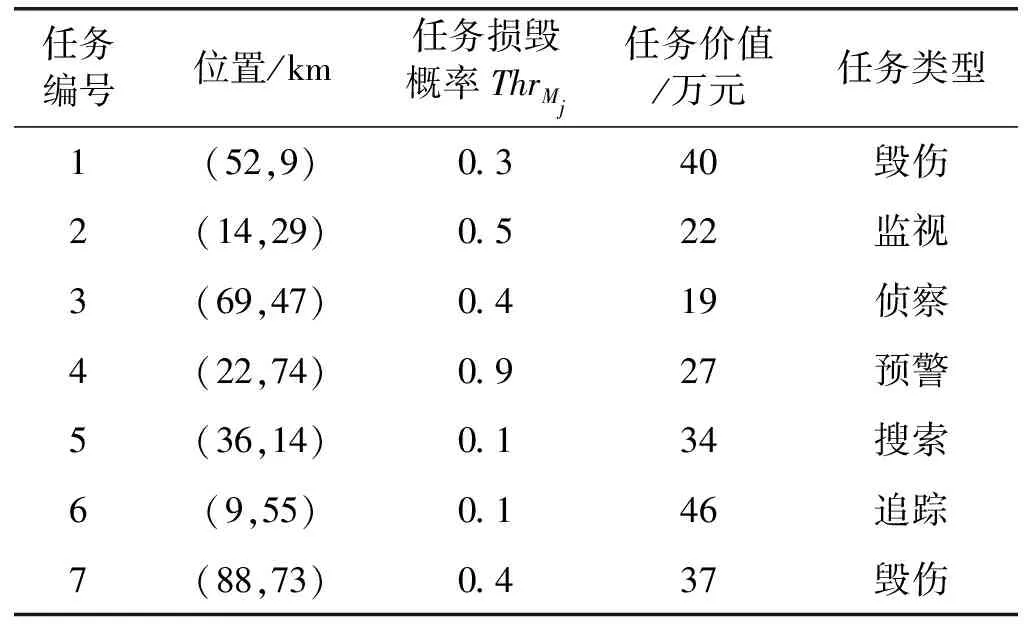
表2 任务各项参数表

续表2

根据表1和表2相关无人机和任务参数可知，毁伤任务1、7、11仅可以由3号和4号无人机完成即xi1、xi7、xi11取值为3、4，监视任务2、10、15仅可由1号、2号、3号无人机完成即xi2、xi10、xi15的取值为1、2或3，其他任务取值以此类推。

对算例中任务按照1～n进行编号，无人机则按照1～m进行编号，无人机总数为4架，则萤火虫个体的搜索范围Ω⊆[1，5)，所得小数均向下取整，由任务数n=15可设定萤火虫个体xi属性为15维，第i个萤火虫表示为xi=(xi1,xi2,…,xi15)。为保证算法收敛到最优解，设置萤火虫的初始种群个体数量N=20，迭代次数t=1 000，其步长因子α、光吸收系数γ、惯性系数ω都由函数定义，分别用粒子群算法、经典萤火虫算法、混沌自适应萤火虫算法对此问题进行求解得到其最优分配序列如表3所示，运用PSO、FA、CAFA三种算法求解迭代对比如图4所示。

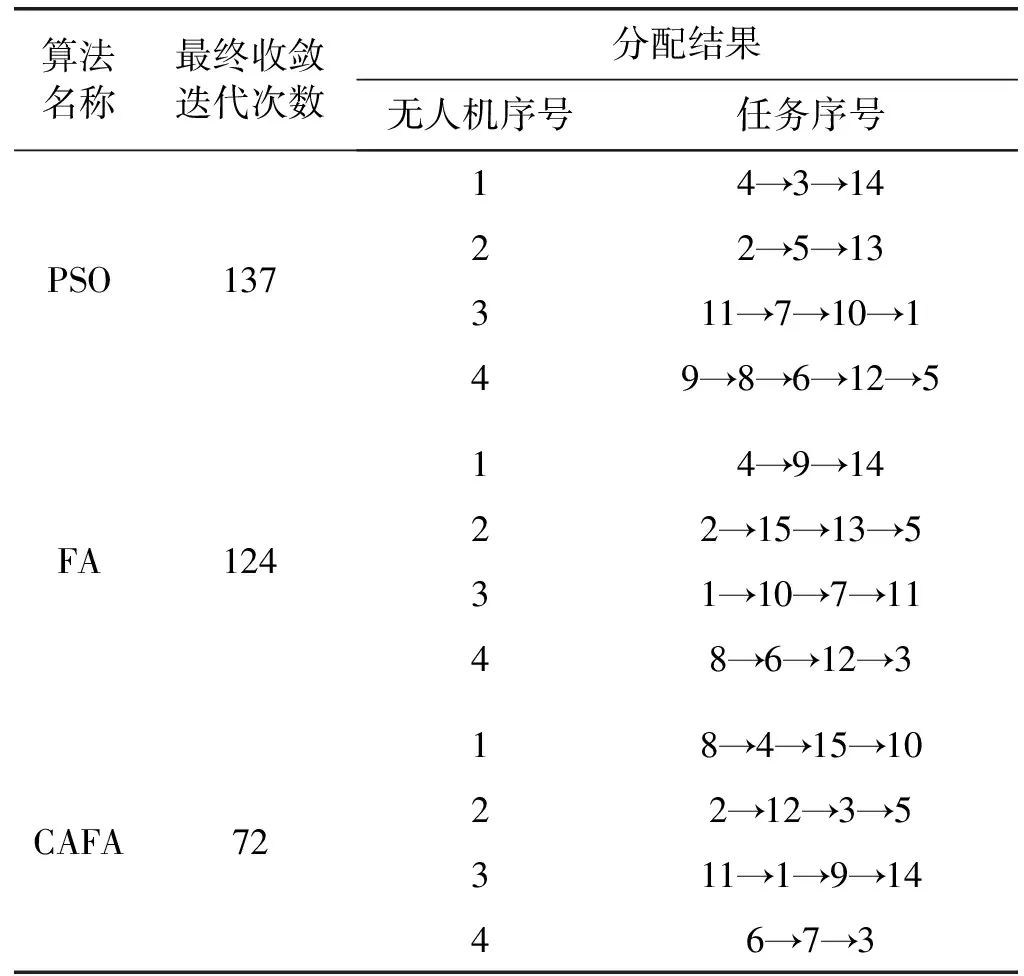
表3 无人机任务分配表

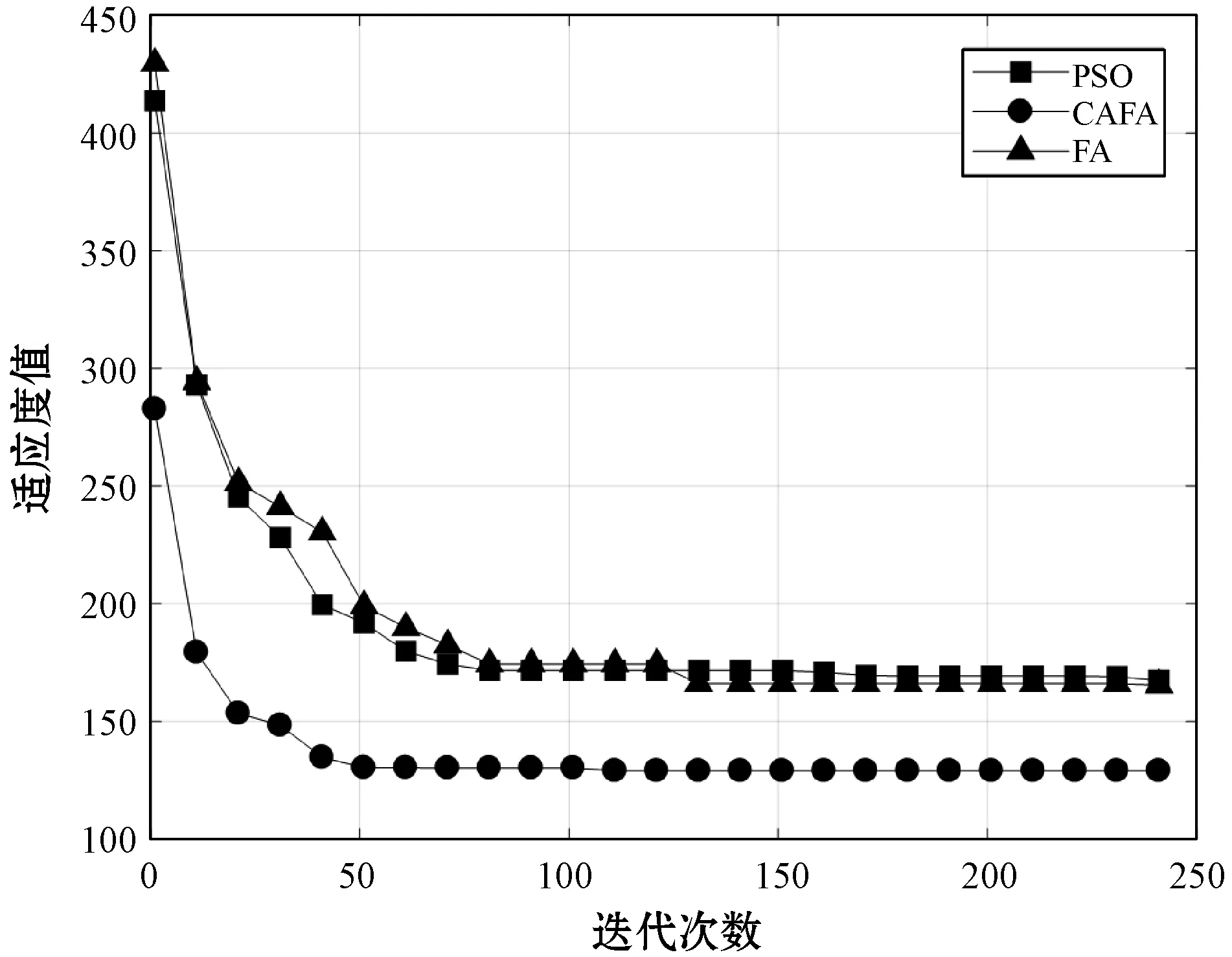
图4 三种不同算法对应迭代对比

可以看出，三种算法的迭代速度有非常大的差别，其中以混沌自适应萤火虫算法的迭代速度最快，在74次左右就收敛到最优值，比粒子群和传统萤火虫算法在迭代速度上有了很大提升。所以混沌自适应萤火虫算法对此问题有更好地适应度。在无人机或任务状态发生改变时，该算法可以更快地响应计算出新的最优分配方案。算法结果对比如表4所示，其飞行路线如图5所示。

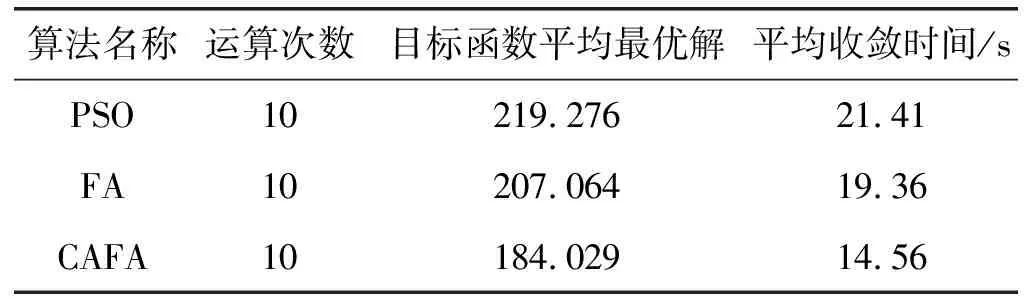
表4 三种算法结果对比表

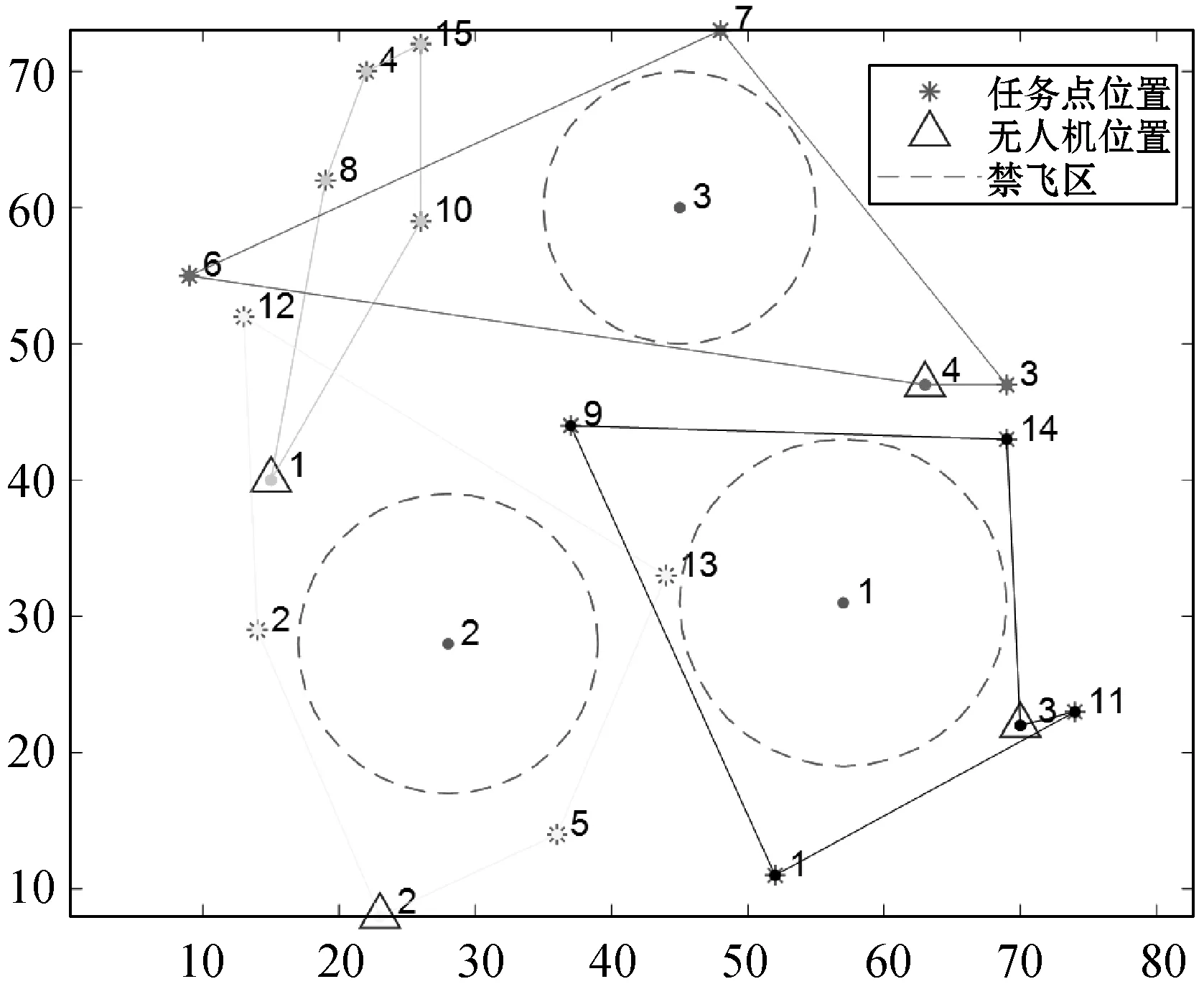
图5 无人机执行任务飞行轨迹

表4给出了PSO、FA和混沌自适应算法的数值结果对比，可以看出针对此问题的解PSO和FA的迭代时间、次数和最终结果相对于混沌自适应算法适应度都相对较差，混沌自适应算法得到的结果相对于PSO和FA精度分别提高了16.07%、11.12%，迭代时间相对提高了31.99%，24.79%，收敛率也相对提高了33.33%、17.65%。实验结果表明CAFA具有较强的全局搜索能力和处理复杂问题的能力，在面对复杂情况时能够更快响应，计算出当前状态下的最佳方案，且能根据作战任务和无人机状态的改变实时更新方案。除此之外，该算法能够很好地提升传统萤火虫算法在初期容易陷入局部最优和随机移动造成的收敛较慢的问题，使得在优化分配任务初期能够更准确、更快地优化当前方案，节省大量时间成本，让无人机群的作战性能进一步提升。

4 结 语

本文针对多数量无人机协同作战任务的分配问题提出一种基于变尺度混沌光吸收强度系数、自适应步长、惯性系数、全局历史最优解的综合萤火虫优化算法。算法能够在搜索前期自适应选择最优方向并加快搜索速度，在收敛后期又可以精确搜索局部最优解，有效地解决由于步长不变而导致的容易在搜索后期跳过最优解、收敛前期速度过慢的问题，具有非常好的收敛精度和速度；能够在一定程度上提升无人机群的协同作战的性能、反应速度并提高处理复杂多变的情况下任务分配速度。考虑地形和环境等影响因素，将算法如何运用于更加复杂的异构无人机协同作战系统，是下一步研究的目标。