基于样条卡尔曼算法的AIS数据修复
苏俊杰,兰培真
(1.集美大学海上交通安全研究所,福建 厦门 361021;2.交通安全应急信息技术国家工程实验室,福建 厦门 361021)
0 引言
目前,AIS是海事分析的主要数据源,但AIS设备由于性能缺陷、信号干扰和设备故障等因素的影响,导致岸基设施接收到的AIS报文在解码后通常会存在部分异常数据,而在数据挖掘分析的过程中,低质量的数据往往会带来巨大的安全隐患[1],因此,亟需开展数据清洗和数据修复工作来提高AIS数据的可用性。
传统的船舶AIS数据修复主要通过插值法实现,文献[2]基于线性插值对船舶轨迹数据进行修复,但仅对近似直线运动的轨迹有较好的修复表现,对曲线运动轨迹的修复则存在较大误差。文献[3-7]基于多项式插值、三次样条插值或Hermite插值对船舶轨迹数据进行修复,能获得较高的修复精度,但修复误差与AIS数据缺失程度呈正相关。采用插值法修复AIS数据,不同特征变量数据的修复过程是相互独立的,没有考虑船位、船速、航向数据之间存在的变化约束,丢失了船舶航行状态特征数据间的关联性。文献[8-9]基于船舶运动学对船舶轨迹数据进行修复,理论上可根据模拟特征变量间的关联性对船舶轨迹数据进行高精度的修复,但AIS数据不能提供足够的参数输入。文献[10-13]基于最小二乘向量机、随机森林、K近邻等机器学习模型对AIS数据进行修复,这些模型虽然能自主学习相似轨迹数据的关联性,在大量准确完整的船舶历史航迹数据支撑下,对AIS数据有比较高的修复精度,但实际上很难获取到准确完整的模型训练样本数据。文献[14-15]基于卡尔曼滤波算法对实时连续变化的系统的动态观测值进行修复,可稳定有效消除传感器获取数据的误差,但相关算法的实现依赖于完整的动态观测数据和状态相关性模型。
本文提出一种样条卡尔曼算法(spline Kalman,SK),拟更准确地修复AIS数据,并利用厦门港及附近水域的历史AIS数据验证算法的有效性。
1 样条卡尔曼算法
卡尔曼滤波算法的基本框架如图1所示。

给定ti-1时刻系统的真实值和ti时刻的系统状态观测值,即可得到ti时刻系统状态的真实值,具体步骤描述如下。
步骤1 根据运动学模型,构建系统状态转移模型,该模型用于描述系统状态ti-1时刻至ti时刻的变化趋势。


可见,卡尔曼滤波算法的基本思路是通过融合当前时刻系统状态的观测值和预测值逼近系统的真实状态值,仅需要系统前一时刻的真实状态值,不需要其他的历史数据,占用内存小,运行速度快,适合用于实时连续变化系统的建模,因此,本文基于卡尔曼滤波算法对AIS数据进行修复。
ti时刻的船舶航行状态Yi可由经度loni、纬度lati、航速vi、航向θi构成的4维特征向量表示,即Yi=(loni,lati,vi,θi),i=1,2,…,n。大多数据修复研究将问题数据集转化为缺失数据集,再通过插值算法对缺失数据集进行填补,这类方法会导致船舶航行状态的观测值存在部分缺失。为方便卡尔曼滤波算法的应用,本文采用局部光滑性较好的分段三次样条插值法[12]对状态观测值进行初步修复,以获得较为准确的状态观测值。


(1)

S3(t)=-Mi[(t-ti+1)3/(6Δti)]+Mi+1[(t-ti)3/(6Δti)]+[xi-
(2)
为求未知数Mi,对S3(t)求导:
(xi+1-xi)/Δti-[(Mi+1-Mi)/6]Δti。
(3)
由此可得:
(4)
同理,在区间[ti-1,ti]可得:
S′(ti-0)=-(Δti-1/6)Mi-1+[(Δti-1)/3]Mi+(xi-xi-1)/Δti-1。
(5)
由式(4)和式(5)可得:μMi-1+2Mi+λiMi+1=di。
其中:μi=-Δti-1/(Δti-1+Δti);λi=Δti/(Δti-1+Δti);di=[6/(Δti-1+Δt)][(xi+1-xi)/Δti)-(xi-xi-1)/Δti-1]=6f[ti-1,ti,ti+1];f[ti-1,ti,ti+1]=[1/(Δti-1+Δti){[(xi+1-xi)/Δti]-[(xi-xi-1)]/Δti-1}。
令式(1)中i=1,式(2)中i=n,则端点方程为:
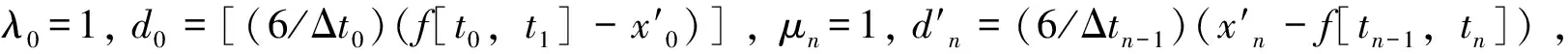
求得Mi后即可获得该状态特征变量x关于时间t的三次样条拟合函数S3(t),从而可对AIS数据中缺失的状态值进行初步修复,得到卡尔曼滤波算法的完整状态观测数据Zi。由于AIS数据的初步修复只考虑了单个状态特征的变化趋势,不足以反映船舶运动特性,因此,本文通过构建船舶航行的状态转移模型来模拟状态特征变化的关联性,对AIS数据进行二次修复,从而还原船舶的运动特性。为便于计算,将航速分解为经度方向航速vlon=vi×cosθi和纬度方向航速vlati=vi×sinθi,则Yi=(loni,lati,vloni,vlati,θi)。由于AIS播发的时间间隔较短,因此,可认为船舶在经纬度方向近似做匀加速运动,则用ti时刻的船舶航行状态来预测ti+1时刻的状态,更新方程为:
其中:F、B、C、D表示相应的矩阵;hlon,hlat分别为单位经度和纬度的实际距离;aloni=(vloni+1-vloni)/Δt;alati=(vlati+1-vlat)/Δt;ωi=(θi+1-θi)/Δt。
预测协方差矩阵为:Pi+1=FPiFT+Q。其中:Pi为ti时刻对应的协方差矩阵,衡量状态特征间的关联性,初始协方差矩阵P0设为对角阵,值取6;Q是用来衡量外界干扰的不确定性的过程噪声,也设为对角阵,取值10-5。
卡尔曼增益矩阵为:Ki+1=Pi+1(Pi+1+R)-1。其中:R是观测噪声,用来衡量观测值的不确定性。

2 检验分析
为检验本文提出的AIS异常数据修复算法的有效性,对厦门港及其周边水域船舶历史AIS数据进行修复,修复步骤如图2所示。选取航行轨迹较为准确完整的385条船舶的AIS数据作为验证数据,取AIS原始数据中的MMSI(maritime mobile service identify)、时间、经度、纬度、航速、航向作为观测数据,以船舶的唯一标识MMSI为一级索引,用以区分不同的船舶轨迹数据,并以时间为二级索引排序观测数据,对重复的AIS数据,仅保留唯一记录;根据经验剔除明显错误数据,保留缺失数据,清洗后的AIS数据如图3所示。
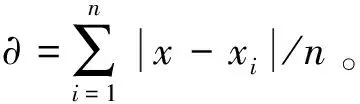

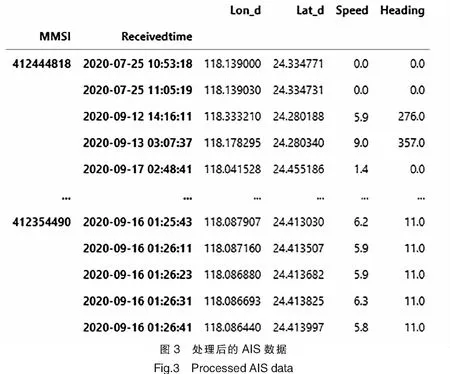
不同缺失率下5种数据修复算法的误差如表1所示。数据修复用时如表2所示。
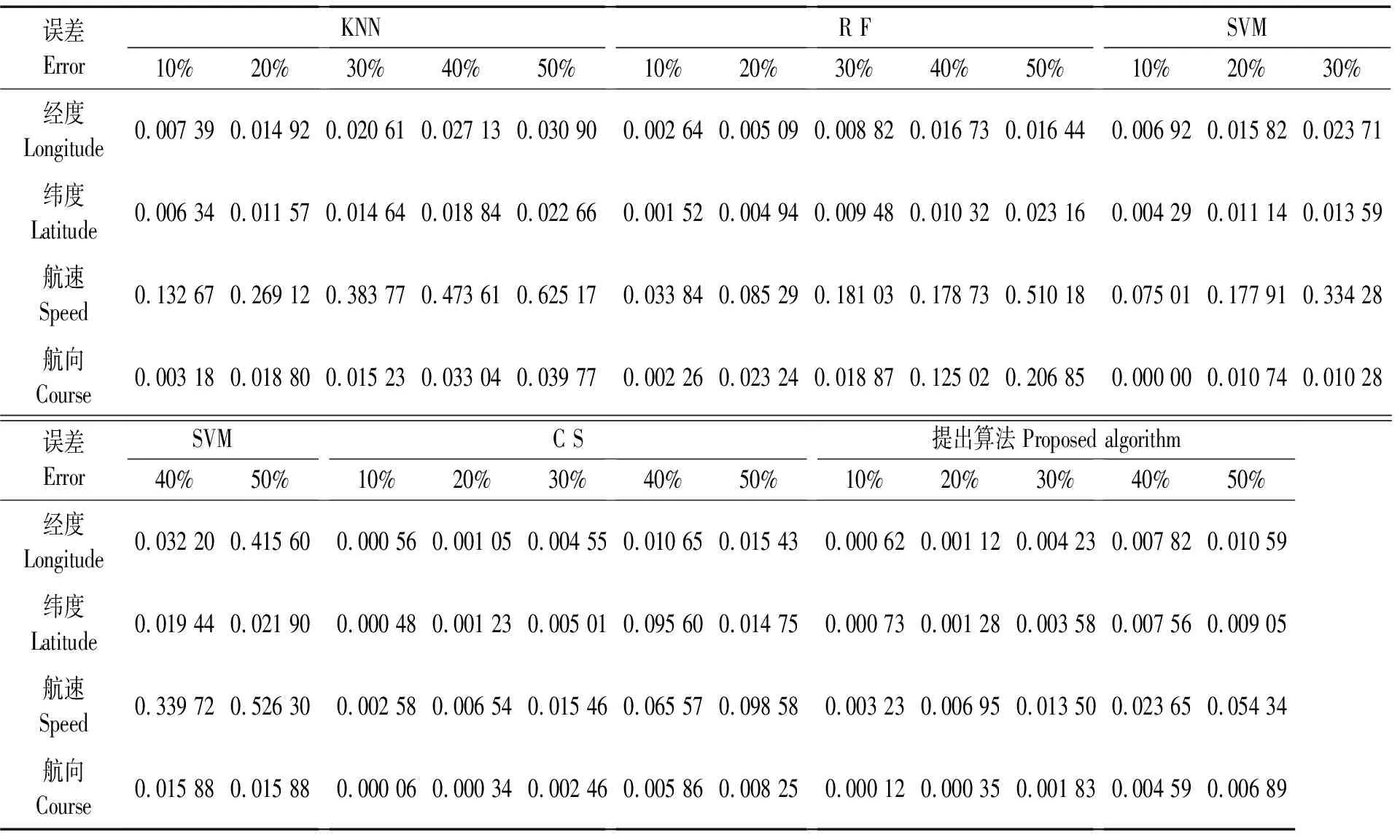
表1 数据缺失的修复误差

表2 不同缺失率AIS数据修复用时
由表1~表2可知,在10%和20%的数据缺失率下,AIS数据修复以分段三次样条插值的效果最优,综合误差分别为0.092%和0.229%,其次是样条卡尔曼算法,综合误差分别为0.118%和0.243%,表明在低缺失率情况下,样条卡尔曼算法对AIS数据的修复效果近似于三次样条插值,优于K近邻法、随机森林算法和支持向量机。而在30%、40%和50%的数据缺失率下,AIS数据修复以样条卡尔曼算法的效果最优,综合误差分别为0.579%,1.086%和2.022%,而对比算法的最优综合误差分别为0.687%,2.291%和3.425%。从整体上看,样条卡尔曼算法在不同缺失率情况下对AIS数据的修复效果最好,表明系统状态转移方程对状态变量起到了一定的约束作用。由表2可知,K近邻法、随机森林法、支持向量机、三次样条插值和样条卡尔曼算法修复不同缺失率情况下的AIS数据的平均用时分别为0.28、1.71、24.13、1.78、1.95 s,除支持向量机算法数据修复效率较低外,其他修复算法修复AIS数据耗时均较小,表明样条卡尔曼算法能满足AIS数据修复时效性和和准确性的要求。
不同缺失率下船舶特征数据修复误差变化曲线如图4所示。

在低数据缺失率的情况下,5种修复算法对AIS数据均具有较好的修复效果,随着AIS数据缺失率的不断增加,5种修复算法的不同状态变量的修复误差都呈现上升趋势,其中,样条卡尔曼算法的修复稳定性最优,三次样条插值算法次之,表明样条卡尔曼算法适用于不同缺失率的AIS数据修复,而K近邻、随机森林、支持向量机等机器学习算法对不同状态变量的修复误差增长尤其明显,可见机器学习算法对数据具有很大依赖性,在数据缺失较多的情况下对AIS数据的修复效果不佳。
3 结论
针对AIS数据的修复提出样条卡尔曼算法,该算法用分段三次样条插值法得到的初步修复数据,并将该数据作为卡尔曼滤波算法的观测数据,并考虑动力学原理和误差干扰因素,建立系统离散状态方程,约束船舶状态变化。检验结果表明,算法能稳定地对不同缺失率的AIS数据集进行修复,修复效率较高,能为基于AIS数据的相关研究提供相对可靠的数据基础。由于卡尔曼算法会受到系统离散状态方程和初次修复算法的影响,因此,在以后的研究中,需要进一步提高状态观测数据的修复精度,并建立更为准确的系统离散状态转移模型,使得AIS数据的修复更加完整准确。

