溶质Marangoni效应对降膜流动稳定性的影响
刘成治,李春曦,周静宜,叶学民
(华北电力大学能源动力与机械工程学院, 河北 保定 071003)
引 言
降膜流动广泛用于精密涂层[1]、燃烧室冷却[2]、降膜换热器[3]、生物医疗[4]等诸多领域,其流动稳定性对于提高涂膜质量、保障降膜换热器换热性能和促进药物吸收具有重要作用。因此,深入研究降膜流动的稳定性问题具有重要的实际应用价值[5-7]。
降膜流动是一种开式流体动力系统,具有显著的对流不稳定特征[8-10]。重力驱动下的降膜系统稳定性可由临界Reynolds 数Rec判别,当液膜流动的Reynolds 数Re超过Rec后,扰动致使液膜流动不稳定,最终导致液膜失稳甚至混沌[11-13]。液膜受热不均或添加表面活性剂后,在温度梯度或活性剂浓度梯度的作用下,液膜表面将会产生表面张力梯度,该类现象分别称为热毛细效应与溶质Marangoni 效应,此类效应对液膜流动的稳定性产生重要影响[14-18],本文仅关注溶质Marangoni效应的影响。
目前,对于受溶质Marangoni效应影响的降膜流动稳定性研究主要以线性稳定性理论为主。Ji 等[19]通过求解O-S 方程,研究了表面活性剂对垂直壁面上降膜流动线性稳定性的影响,结果表明:在中等Reynolds 数条件下,溶质Marangoni 效应在液膜表面引起了扩散波,并证明了表面活性剂的解吸附是扩散波产生的主要原因。Blyth 等[20]分析了倾斜平板上含表面活性剂的降膜流动线性稳定性,结果表明:表面活性剂具有促进液膜稳定的作用,且添加表面活性剂可有效提高Rec。Pereira 等[21]考察了溶质Marangoni效应对降膜流动非线性区的影响,发现表面波的扰动演化为孤立脉冲,其振幅和速度随溶质Marangoni 效应增强而减小。Georgantaki 等[22]实验研究了SDS 活性剂对降膜流动稳定性的影响,指出加入活性剂后,入口初始扰动显著衰减,一次失稳的Rec提高了一个数量级,并在一定参数下扰动会触发二次失稳。Hu 等[23]基于加权残差模型研究了表面活性剂影响下的降膜流动线性稳定性,并考虑了表面弹性和表面黏度对流动的影响,结果表明:提高表面弹性可降低扰动增长率,增大Rec,同时抑制表面波的色散效应;提高表面黏度则降低了扰动增长率与截断波数,但不影响Rec大小。
综上所述,表面活性剂对降膜系统的稳定性有重要影响。在以往的研究中[20-21,23],所得临界Reynolds数与Weber数无关,并极少考虑Peclet数对线性稳定性的影响。而有研究表明[24],无表面活性剂情形下,提高Weber 数可增大降膜流动稳定区。因此,本文将在Blyth 等[20]研究基础上,进一步考虑Weber数与Peclet数对临界Reynolds数的影响,提出包括Weber数、Marangoni数、壁面倾角和Peclet数在内的临界Reynolds 数表达式,进而分析相关参数对流动线性稳定性的影响,并通过数值模拟探究溶质Marangoni 效应作用下表面波的时空演化特征以及相关参数对流动非线性特征的影响。
1 理论模型
如图1 所示,在倾角为θ的固体基底斜面上均匀附着一层厚度为h*的薄液膜,初始液膜厚度为,液膜受到扰动后表面呈现波状,波长为l*。该液膜在重力作用下沿斜面向下流动,重力加速度为g,液膜表面分布有不溶性表面活性剂。假设该液膜为不可压缩牛顿流体,其密度为ρ*,动力黏度为μ*。忽略液膜表面外界的气体黏度与液膜蒸发的影响,不考虑分子间作用力,上角标“*”代表有量纲量。

图1 含不溶性活性剂薄液膜沿斜面下降流动示意图Fig.1 Schematic diagram of a liquid film flow over an inclined plane in the presence of an insoluble surfactant
本文采用长波近似法研究中小Reynolds数范围内液膜的稳定性,其优势是避免直接求解O-S 方程特征根所带来的计算烦琐的问题[8,21]。在长波近似法的假设下,本文基于Navier-Stokes 方程、连续性方程与活性剂扩散方程[10],并在基底处采用无滑移无渗透边界条件,自由界面处考虑切向应力、法向应力平衡边界条件以及运动学边界条件[21],最终推导出如下形式的液膜厚度与活性剂浓度演化方程:
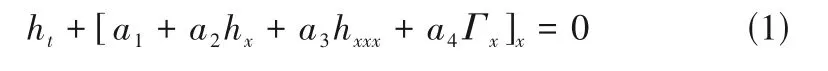

式中,Re为Reynolds 数,中小Reynolds 数条件下Re取值范围为0~10;Pe为Peclet 数,表征表面活性剂的扩散程度,其值与表面活性剂的种类有关,取值范围为10-1~103;We为Weber 数,表征液膜表面张力与惯性力之比,本文引入S=ε2We表示经缩小后的Weber数,取值范围为0~10;M为Marangoni数,表征溶质Marangoni 效应的强度,取值范围为0~10;U*为特征速度,U*=ρ*gh*2sinθ/3μ*;ε=h*/l*≪1,表示液膜厚度与表面波波长的比值;Ds*为表面活性剂的扩散系数,表征表面活性剂的扩散强度。演化方程推导过程中假定表面张力与活性剂浓度之间符合线性关系式[25]:σ*(Γ*)=-α*(Γ*-),其中是参考浓度,σm*为Γm*所对应的表面张力,α*=-(∂σ*/∂Γ*)为表面张力系数,表征表面张力随活性剂浓度变化的剧烈程度。
2 含表面活性剂的降膜流动线性稳定性分析
2.1 色散方程的推导
采用摄动法对基态流施加小扰动可得:

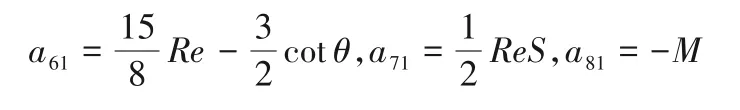
将无穷小扰动按照正则模法展开为(η,γ) =(η̂,γ̂)eikx+ωt,其中复波速ω=ωr+iωi,ωr表示扰动增长率,ωi表示扰动频率,实数k表示扰动波数,(η̂,γ̂)代表液膜厚度与活性剂浓度的扰动振幅,将展开后的无穷小扰动代入式(5)和式(6)可得色散关系式:
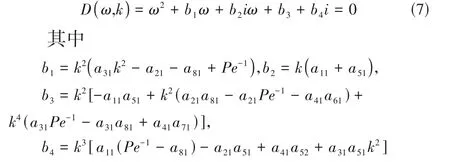
式(7)为以复波速ω为未知数的一元二次方程,其复数根的实数部分与虚数部分分别定义为扰动增长率ωr与扰动频率ωi,具体如下:

2.2 液膜流动中性稳定状态

式中,kc表示截断波数。液膜流动在0<k<kc为失稳区,其他区为稳定区。
2.3 线性稳定性分析
下文主要关注Re、M、θ、Pe和S对液膜流动稳定性的影响,若无特殊说明,Re= 1,M= 1,θ= 60°,Pe=100,S= 4.5。
图2 和图3 为最大扰动增长率ωr,m和最危险波数km随Re的变化,表征流动的最不稳定状态。图2表明:当Re<Rec时,ωr,m= 0,即扰动在任意波数下均不随时间增长,流动保持稳定;当Re>Rec时,ωr,m>0,ωr,m随Re的增大近似呈线性增长,衍生出失稳区并随Re增加而扩大,最危险模式下液膜扰动增长越来越剧烈。增大M与减小θ降低了ωr,m的线性增长率,说明溶质Marangoni 效应的增强与惯性因素的减弱抑制了最危险模式下扰动的增长,有利于液膜的稳定流动。

图2 最大扰动增长率ωr,m随M和θ 的变化(“ ”表示临界状态)Fig.2 Variation in the maximum perturbation growth rate ωr,m with M and θ (“ ” indicates a critical state)
图3 表明:当Re≤Rec时,km= 0,此时ωr,m≤ 0 在任意波数k时恒成立,液膜流动处于稳定状态。当Re>Rec时,最危险波数km随Re增大而提高,液膜流动的最危险模式向短波区扩张,表明增大Re不利于液膜的稳定流动;增大θ与减小M均减弱了Marangoni应力对惯性力的抑制作用,并使流动最危险模式向短波区移动,因此缩小了液膜的稳定区,降低了液膜流动的稳定性。例如无表面活性剂(M= 0)或基底竖直摆放时(θ= 90°),Rec最小,此时km最大,液膜的失稳区范围最大。

图3 最危险波数km随M和θ 的变化(“ ”表示临界状态)Fig.3 Variation in the most dangerous wave number km with M and θ (“ ” indicates a critical state)
图4 反映了Marangoni 数M对ωr+与相速度ci的影响。图4 表明:提高M减小了液膜在失稳区的扰动增长率ωr+,同时使液膜截断波数kc向长波区移动,从而减小了失稳区内液膜扰动增长与失稳区面积,表明溶质Marangoni效应抑制了失稳状态下扰动的发展。在无表面活性剂(M= 0)情形下,相速度ci为一常数,表明表面波是非色散波,其相速度不随扰动波数的变化而变化;添加表面活性剂后,随波数k的增大相速度ci先降低后升高,表面波的演化受色散效应影响。在长波区(k< 0.8)内,ci在最危险波数km附近存在一极小值点,此时表面波的色散效应最强,液膜扰动的发展最显著。随着M的增大,相速度曲线左移,ci极小值增大,表明溶质Marangoni 效应的进一步增大将削弱表面波的色散。
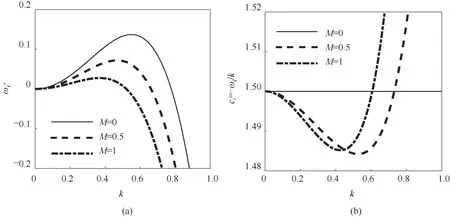
图4 扰动增长率ωr+和相速度ci随M的变化Fig.4 Variation in perturbation growth rate ωr+ and phase speed ci with M
图5 为不同参数下的中性稳定曲线。由图5 可知,增大M使中性稳定性曲线下移,Rec增大,液膜失稳区逐渐收缩,体现了溶质Marangoni效应对液膜流动的稳定作用。提高θ则导致中性稳定曲线上移,Rec减小,失稳区扩大。提高Weber 数S将减小失稳区面积,促使流动稳定,但不影响Rec的大小,这与Dholey 等[24]在研究无表面活性剂时降膜流动稳定性中的结论一致。Pe表征活性剂单体扩散速度的大小,与液膜表面活性剂分子的扩散系数成反比。Pe越大,活性剂分子在液膜表面的扩散速度越慢,Marangoni应力对惯性力的阻碍作用越弱,液膜越趋于失稳。

图5 不同参数下的中性稳定曲线(“ ”表示临界状态)Fig.5 Neutral stability under different parameters (“ ” indicates a critical state)
图6对比了本文结果与Blyth等[20]基于直接求解O-S 方程所得结果,实线表示本文结果,虚线表示Blyth 等[20]的结果。图6(a)表明,在Stokes 流假设下(Re= 0),M= 0 时,两种方法所得到的ωr+均小于0,液膜流动始终处于稳定状态,且两条曲线在小波数范围内(k< 0.5)的数据基本吻合。图6(b)表明,采用长波近似法所得出的中性稳定曲线相较于直接求解O-S 方程得出的结果而言,曲线整体略微向x轴负半轴移动,流动稳定区有所收缩,但变化幅度不大,M= 0与M= 1时对应的Rec分别下降了0.41与0.50。
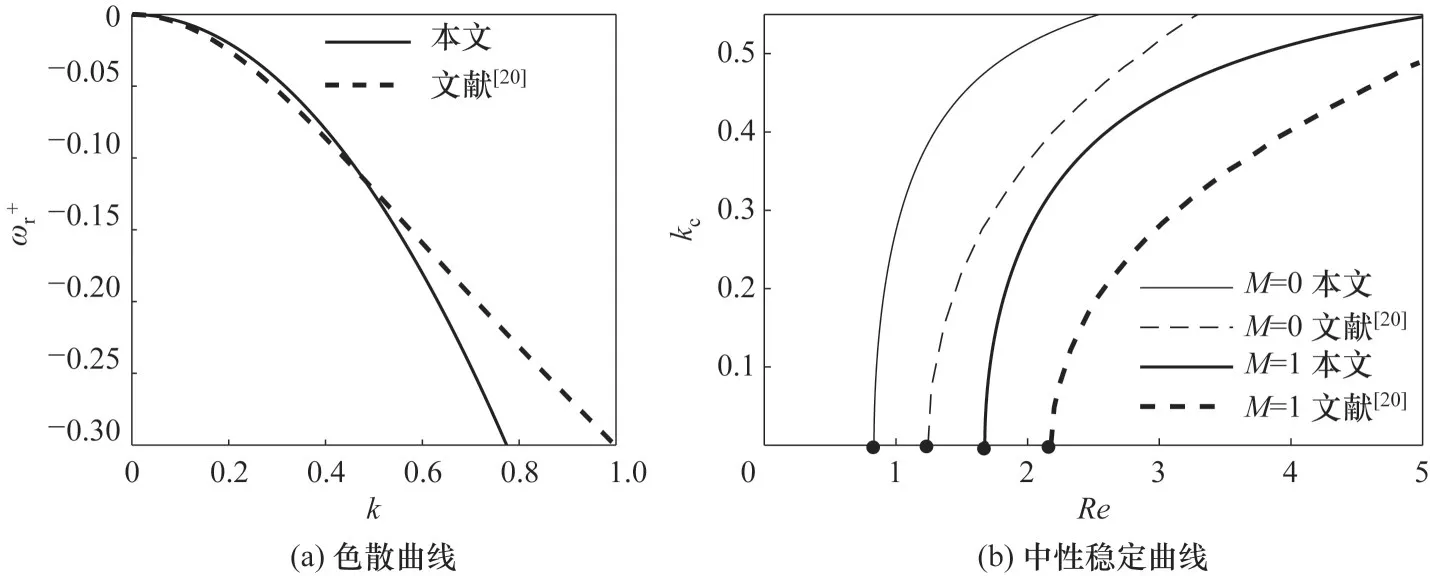
图6 本文结果与文献[20]结果的对比(“ ”表示临界状态)Fig.6 Comparison of the results of this paper with that of Ref.[20](“ ” indicates a critical state)
3 表面波演化历程
3.1 初始条件与边界条件
为进一步探究溶质Marangoni 效应对表面波的影响,采用偏微分方程数值求解软件“FreeFEM++v4.7”求解非线性演化方程组式(1)和式(2),该软件具有网格自适应和移动网格生成的特点,目前已广泛用于相关领域的研究中[26-29]。为模拟扰动的演化,根据演化尺度选取0<x< 200的一维区域进行计算,并设置初始扰动振幅为基本流膜厚的1%,如式(11)所示,相应的边界条件如式(12)所示。经过网格无关性验证后,在满足精度与减少计算时间的条件下,设置计算域网格数为20000,时间步长为0.1。
初始液膜厚度与活性剂浓度分布[30]为:

平板两端液膜厚度与活性剂浓度分布边界条件为:
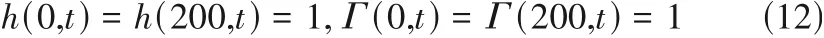
3.2 表面波演化特征
图7 为溶质Marangoni 效应对表面波演化的影响。无表面活性剂(M=0)时,初始扰动最终演化为孤立波。添加表面活性剂(M>0)后,表面波由于色散效应的影响,衍生出快波与慢波。一方面,快波演化受溶质Marangoni 效应抑制,其振幅随M的增大而减小,这与线性稳定性结论一致;另一方面,在色散效应影响下,慢波随时间演化出了多峰波状结构,Georgantaki 等[22]的实验同样观测到了这一现象。进一步增大M则抑制了慢波的发展,使其振幅衰减,即溶质Marangoni 效应抑制了初始扰动的发展。
图8 展示了溶质Marangoni 效应对活性剂浓度分布的影响。由图8可知,随着液膜的流动,活性剂分子逐渐向下游区域扩散并呈现波状分布。对比图8(a)、(b)可知,随着M的增加,活性剂浓度变化逐渐趋于平缓,即溶质Marangoni效应促进了活性剂分子的重新分布。观察图7 可知,在M= 0 时,上游区液膜厚度分布均匀,下游区液膜初始扰动演化为快波;而当M> 0时,随着液膜的流动,上游区出现了慢波并且慢波振幅随时间逐渐增长,而下游区的快波振幅则随时间逐渐衰减,这实质上是活性剂浓度分布不均所产生的Marangoni 应力作用的结果。M相同时,图7 中慢波区液膜厚度的波峰基本对应图8中活性剂浓度的波谷,二者相位差略小于180°,而图7 中快波区液膜厚度的波峰对应图8 中活性剂浓度的波峰,Marangoni应力驱动流体从高浓度处流向低浓度处,这一流动叠加液膜整体从左向右流动之后,导致慢波振幅随时间增加,而快波振幅随时间衰减,且慢波与快波间的距离不断增大。

图7 溶质Marangoni效应对表面波演化的影响(实线箭头表示慢波,虚线箭头表示快波)Fig.7 Influence of solutal Marangoni effect on surface waves evolution(solid arrow represents slow waves, and dashed arrow represents fast waves)
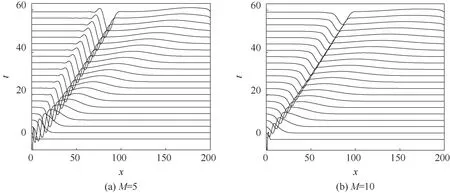
图8 溶质Marangoni效应对活性剂浓度分布的影响Fig.8 Influence of solutal Marangoni effect on the distribution of surfactant concentration
图9 为Peclet 数Pe对表面波演化的影响。图9表明,提高Pe增大了慢波振幅,促使慢波后续演化出多峰波状结构。提高Pe即减缓了活性剂分子的扩散速度,阻碍了活性剂分子在液膜表面的扩散,且从活性剂浓度演化方程式(2)可知,Pe直接影响活性剂浓度Γ的二阶导数项,因此在活性剂浓度变化剧烈的慢波区,Pe增大导致活性剂浓度梯度作用被放大,局部Marangoni 应力提高,从而增大了慢波振幅,降低了液膜流动的稳定性。Pe的变化对快波的演化基本无影响,这是因为快波区活性剂分布相对慢波区较为均匀,活性剂浓度Γ的二阶导数项较小,因而Pe变化对快波的影响并不显著。
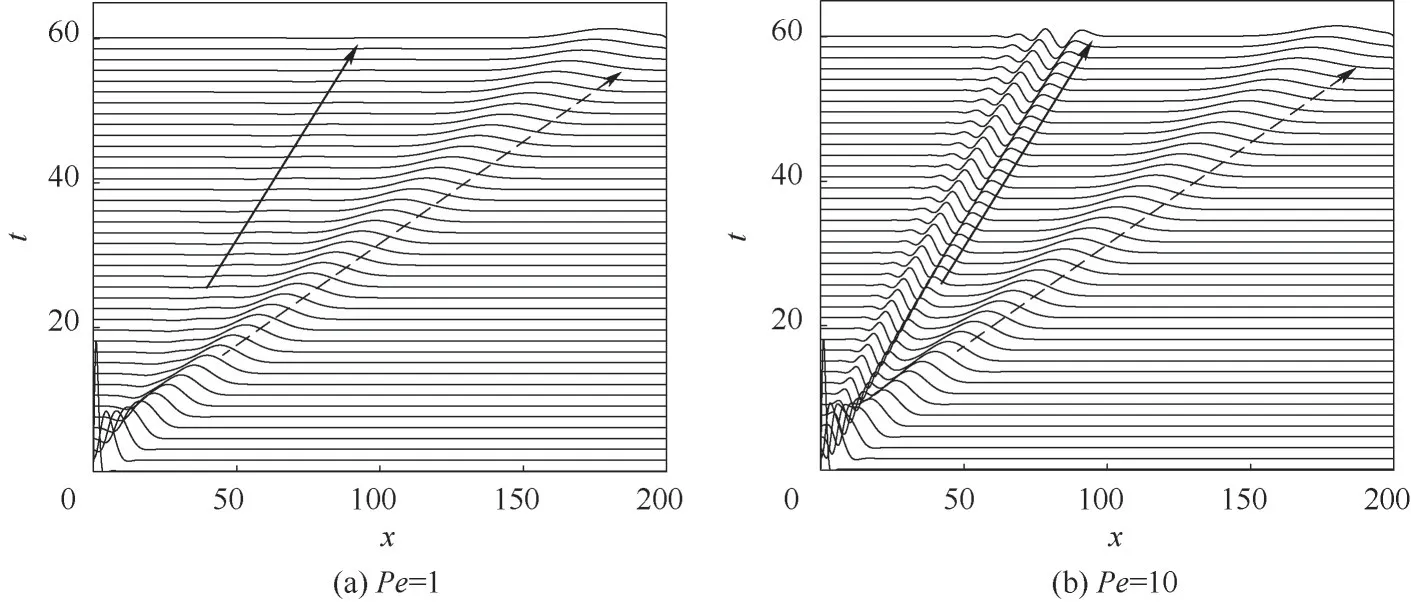
图9 Peclet数对表面波演化的影响(实线箭头表示慢波,虚线箭头表示快波)Fig.9 Influence of Peclet number on surface waves evolution (solid arrow represents slow waves, and dashed arrow represents fast waves)
图10 为Weber 数S对表面波演化的影响。图10 表明,降低S增强了慢波振幅,提高了慢波的波数,不利于液膜的稳定。从液膜厚度和活性剂浓度的演化方程式(1)和式(2)可知,S直接影响液膜厚度的四阶导数项,因此对液膜厚度变化剧烈的慢波区影响显著,对液膜厚度变化平缓的快波区影响较小。由前文分析可知,在慢波区,液膜厚度与活性剂浓度存在略小于180°的相位差,同时,根据本文S的定义式,减小S意味着减小表面张力的作用,导致表面波演化更剧烈,在后续演化过程中慢波的波数将逐渐增加,因此慢波会演化为多峰结构,慢波振幅也逐渐加大。这一点与图7 中减小M的作用类似,但减小S的效果更为显著。
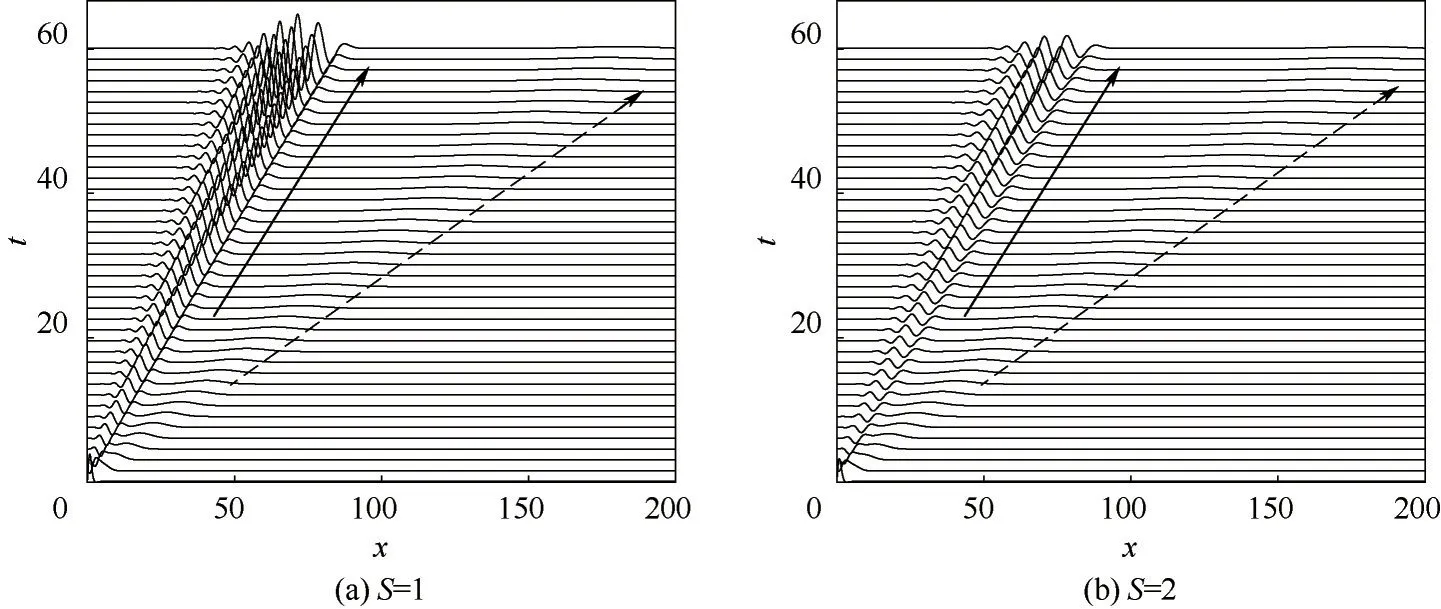
图10 Weber数对表面波演化的影响(实线箭头表示慢波,虚线箭头表示快波)Fig.10 Influence of Weber number on surface waves evolution (solid arrow represents slow waves, and dashed arrow represents fast waves)
4 结 论
本文基于长波近似法推导出综合考虑Weber数S、倾角θ、Peclet 数Pe、Marangoni 数M的色散关系式与临界Reynolds 数Rec表达式,研究了溶质Marangoni效应作用下的降膜流动线性稳定性,并通过数值模拟探究了溶质Marangoni 效应作用下表面波的时空演化特征,主要结论如下。
(1)对于受溶质Marangoni 效应影响的降膜流动,提高M即增大了溶质Marangoni效应对液膜流动的影响。这将导致Rec的增大并降低失稳区内的扰动增长率与截断波数kc,由此减小液膜失稳区范围,抑制失稳区内扰动波的增长,有利于液膜流动的稳定,而增大Re与θ则降低了液膜流动的稳定性。
(2)S与Pe均对液膜流动的稳定性产生重要影响:提高S可增大Marangoni 应力对液膜流动的稳定作用,缩小失稳区范围,但并不改变Rec;增大Pe可减缓活性剂分子在液膜表面的扩散速度,阻碍活性剂分子的铺展,不利于液膜的稳定。
(3)表面波的演化结果表明:与无活性剂时液膜流动相比,溶质Marangoni效应引起了表面波的色散效应,使初始扰动分离为快波与慢波,而慢波在后续演化中进一步发展为多峰波状结构;进一步增强溶质Marangoni效应则减小了活性剂浓度梯度,同时减小了快波与慢波的振幅,由此抑制了表面波的演化;提高Pe导致活性剂浓度梯度作用被放大,局部Marangoni应力提高,从而降低了液膜流动的稳定性;减小S意味着减小了表面张力的作用,导致表面波演化更剧烈,不利于液膜的稳定流动。

