高压涡轮气动优化与分析

杨伟平，房兴龙，欧阳玉清，李恩华，曾 飞

(1.中国航发湖南动力机械研究所，湖南 株洲 412002；2.中小型航空发动机叶轮机械湖南省重点实验室，湖南 株洲，412002)

1 引言

涡轮是燃气轮机及航空航天等动力装置的核心部件，其性能好坏直接关系到整个系统能否高效、可靠运行。邹正平[1]、王保国[2]等针对涡轮的气动设计和流动机理进行了大量研究，为涡轮气动设计及优化提供了有益的参考。但关于涡轮转静轴向间距的选取，却有不同观点。柯别列夫等[3]认为，在考虑结构可靠的基础上，应该减小转静之间的轴向距离，且该值约为0.2 倍工作叶片弦宽。文献[4]则认为，为避免转静之间气流的互相干扰与激振，并考虑冷热态工况下轴向长度的变化，带冠叶片与其前面导叶的轴向间距应不小于导叶轴向弦长的20%；当动叶不带冠时，希望间距增大1 倍以上。高怡秋[5]采用数值模拟方法进行研究表明，涡轮的流量和效率随轴向间距的减小而减小，但随着间距的增大，流量和效率先增大后下降。可见，前述各研究所得结论有一定差异，为此有必要针对涡轮转静轴向间距开展进一步研究。

此外，业界对轴流叶轮机械优化也进行了较多研究。张剑等[6]基于iSIGHT，集成涡轮平面叶栅造型程序、叶片三维积叠程序、流道设计软件、网格划分软件TurboGrid、流场分析软件CFX，开发了涡轮三维叶片气动优化集成平台；并对弹用发动机低压涡轮导向器进行了三维气动优化设计。结果表明，导向器能量损失较原型降低7%。米攀等[7]基于iSIGHT，通过集成三维造型程序、CFD 计算程序与多岛遗传算法，搭建了三维造型优化设计系统。针对某压气机第一级静子根区存在的角区分离进行优化。结果表明，优化后的叶型有效削弱了第一级静子的角区分离，使得根部区域的总压恢复系数增加了1.8%，改善了级间匹配，提高了压气机效率。王婧超等[8]基于iSIGHT，搭建了全三维涡轮叶片一体化多学科优化设计系统，并将之运用于涡轮优化，使涡轮性能得到明显提高，研究还表明，所搭建系统稳定、高效，具有应用于工程实践的可行性。何松[9]在iSIGHT 中集成UG、ICEM、CFX 软件，建立起叶轮蜗壳参数化建模、网格划分、流场数值计算对比的自动优化系统，选取NSGAII 优化算法，提升了设计工况下涡轮泵的水力效率和扬程目标。以上研究表明，可以根据需要，在iSIGHT 中集成不同的软件，以延续原设计体系；且所搭建的系统具有良好的兼容性和鲁棒性，同时也提供了丰富的多目标优化算法，为优化设计提供了较好的平台。

综上所述，由于本文所优化的涡轮，其转静轴向距离根据经验选取，而前人对间距选取的观点不统一，因此有必要对其进行优化。同时，为了延续原有的涡轮设计和性能评价体系，基于iSIGHT，集成Numeca、CFX 软件，开发了三维气动优化集成平台，并以涡轮效率和级出口绝对气流角为目标，对涡轮进行多目标优化。以期在不改变子午流道几何、考虑冷却叶片及与下游低压涡轮匹配的需求，且保持涡轮进口流函数和膨胀比基本不变的条件下提升涡轮性能。

2 数值模型与优化思路

研究对象为某发动机的高压涡轮，其导叶和动叶均带冷却设计。采用商用软件CFX 17.2 进行三维CFD 计算与分析，计算域如图1 所示。其中，湍流模型为两方程 k−ε 模型，工质假设为燃气，采用变比热计算。三维计算考虑了涡轮冷却、封严等二股气流的影响，导叶的冷却气膜孔、封严气采用源项进行模拟。为方便动叶优化，暂不添加源项。考虑叶身、端壁、缘板、外环等流道区域粗糙度影响，设置固壁粗糙度等沙粒直径为0.02 mm。高压涡轮转子叶片叶尖间隙取固定值0.50 mm。

图1 计算域示意图Fig.1 Computational domain

对于涡轮气动设计，尽管一维设计参数对涡轮气动性能起决定作用，但考虑到原高压涡轮存在着与低压涡轮的匹配及结构设计限制问题，因此不再进行一维参数及子午流道的优化。对于三维而言，涡轮气动性能的好坏与叶型直接相关。叶型除了决定其本身负荷及负荷形式外，由其所构成的三维叶片喉部面积，更是决定了单级涡轮的流量、功分配以及级出口马赫数和气流角的径向分布，继而影响一维设计参数，使得三维设计参数与一维设计参数偏离。为此，本研究在优化的同时，尽量保持涡轮导叶进口流函数不变，将表征涡轮转静叶片功分配的反力度也限定在一定区间内，使级内的匹配不发生较大变化。根据对原型涡轮三维数值模拟结果的分析，主要从以下两点进行优化：

(1)轴向间距。原型轴向间距根据经验参数选取，而经验参数一般有一定的范围，取值可能不是最佳，需进一步优化。

(2)动叶叶型。原型导叶总压恢复系数较高，损失较小，且导叶采用大冷气量进行冷却设计，结构较复杂，为此不对导叶叶型进行优化；而动叶受二次流影响较严重，且进口气流存在一定的攻角，因此着重对动叶叶型进行优化。动叶的优化需要考虑冷却叶片、强度设计以及与下游低压涡轮的匹配问题。

3 优化结果与分析

3.1 转静轴向间距优化

在平均中径高度上，原型涡轮转静轴向间距L约为导叶轴向宽度 Ls的0.387 倍，如图2 所示。由于该值根据经验选取，故对其进行优化。选取平均中径高度上转静轴向间距，分别为导叶轴向宽度的0.200、0.250、0.300、0.350、0.387(原设计)、0.400、0.450、0.500 倍作为算例。图3 给出了涡轮进口流函数、膨胀比和效率随相对转静轴向间距的变化。其中，涡轮进口流函数由公式(1)计算得到。可以看到，涡轮进口流函数基本保持不变。所有算例中，能量反力度均在0.428～0.431 之间，说明涡轮级内匹配也基本保持不变。涡轮效率随着相对轴向间距的增大先增大后减小，存在一个最佳的轴向间距(为导叶轴向宽度的0.300 倍，约9.3 mm)，使得涡轮效率提高约0.2%。根据多个型号的结构设计经验，该轴向间距满足结构方面的要求。据此，所研究的高压涡轮，当轴向间距为导叶轴向宽度的0.300 倍时，不仅能满足结构设计要求，同时也能使涡轮性能最佳。

图2 轴向尺寸示意图Fig.2 Sketch map of axial spacing in the meridian plane

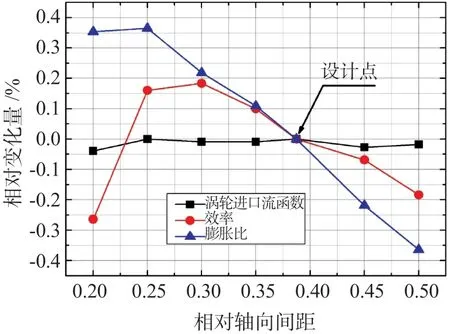
图3 进口流函数、效率和膨胀比随相对轴向间距的变化Fig.3 Flow function,efficiency and expansion ratio vary with the relative axial spacing

式中：min为涡轮进口流量，Ttin为涡轮进口总温，ptin为涡轮进口总压。

3.2 动叶优化

3.2.1 叶型参数化

根据3.1 节研究结果，在后续的动叶优化中，转静轴向间距均采用0.300 倍导叶轴向宽度。采用Numeca 中的Autoblade 模块，对转子叶片进行参数化，选用与Pritchard[10]参数法相似的参数化方法。选取根、中、尖3 个截面进行参数化拟合，进出口构造角及安装角如图4(a)所示;吸力面和压力面均选择4 个控制点，如图4(b)所示。

图4 叶型参数化示意图Fig.4 Sketch map of blade parameterization

为校验参数化拟合效果，对原型叶片和参数化后的叶片进行了CFD 验算，结果见表1。表中，相对变化量。可知，参数化后的叶片较原型叶片的涡轮性能变化在0.20%以内，说明参数化后叶片与原型的性能基本接近，参数化效果较好，可以用于后续的优化研究。

表1 参数化前后涡轮性能对比Table 1 Performance comparison of the turbine before and after parameterization

3.2.2 优化平台及优化问题描述

为了延续使用CFX 作为涡轮数值计算和性能评估的软件，基于iSIGHT，集成Numeca、CFX软件，开发了三维气动优化集成平台。采用Numeca 中的Autoblade 模块实现叶片的参数化，Autogrid 模块实现网格的划分，Screening 模块实现叶片参数化到网格划分的流程自动掌控；采用CFX 中的Pre模块实现数值模拟的前处理，Solve 模块实现数值求解，Post 模块实现后处理；最终通过iSIGHT，实现涡轮叶型参数化、网格划分、三维数值计算及结果的自动处理与优化。

考虑高压涡轮与低压涡轮的匹配问题，在提升高压涡轮效率的同时，应尽量使高压涡轮级出口气流参数变化较小。而级出口绝对气流角2α、级出口马赫数Ma2和反力度Ω 相互制约，为此选择涡轮效率ηtt和2α 作为优化目标。优化目标函数如公式(2)所示，优化流程见图5。根据多轮的优化经验，在优化目标中，ηtt部分给定0.9 的权重系数，α2部分给定0.1 的权重系数，得到优化目标ϖ 。由于α2较原型的不宜变化过大，因此限制在72°～79°之间。考虑涡轮级内匹配及轴向力等因素，Ω 限制在0.42～0.46 之间。原型动叶采用冷却叶片设计，考虑到冷却叶片的需求，保持原叶片的前缘半径、尾圆半径以及厚度不变，只选取根、中、尖3 个截面的进口构造角，出口构造角，安装角，尾缘楔形角δ，以及吸力面的4 个控制点，共24 个参数作为优化变量，且变化范围均为正负10%。由于NSGA-Ⅱ具有良好的探索性能，根据优化算法的使用经验及相关文献[11-12]，最终选择NSGA-Ⅱ全局多目标优化算法。在算法设置中，Population Side 设置为16，Number of Generations 设置为25，样本数为400，满足推荐值20～200 之间的要求。Crossover Rate 设为0.9，在推荐值0.6～1.0 之间。其余按默认设置。

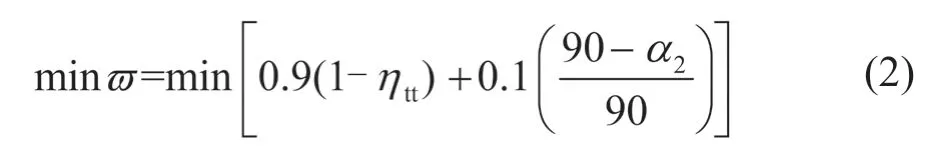
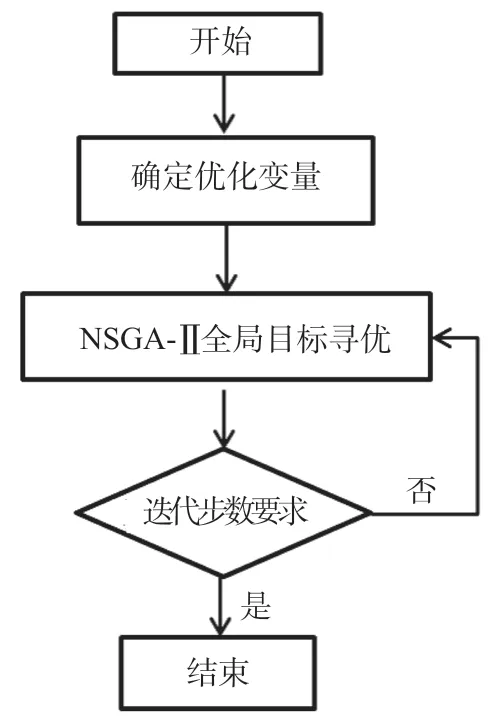
图5 优化流程示意图Fig.5 Flow path of optimization

3.2.3 优化结果与分析

图6 示出了吸力面控制点 ts1随优化步数的变化趋势。可看出，作为优化变量的代表，其基本达到收敛。图7 示出了涡轮效率随优化步数的变化，可见效率在一个区间内震荡。根据优化结果，第322 个样本点涡轮性能最佳。表2 给出了优化前后涡轮性能的对比。表中，相对变化量ξ=((Aopt−Aori)/Aori)×100%。可见，优化后涡轮进口流函数基本保持不变，膨胀比下降了1.099%，涡轮效率提高了0.799%，功率提高了0.785%，转子能量损失系数下降了8.561%，而涡轮级出口气流角仅下降2.895%，约2.3°。原型涡轮的能量反力度为0.437，优化后涡轮的能量反力度较原型提高了0.023。图8 给出了设计转速不同膨胀比工况下，优化前后涡轮性能对比。图中，ori 表示原型，opt 表示优化后。可以看到，优化后的涡轮性能较原型的有了较大提升，说明优化效果较好，优化方法有效。

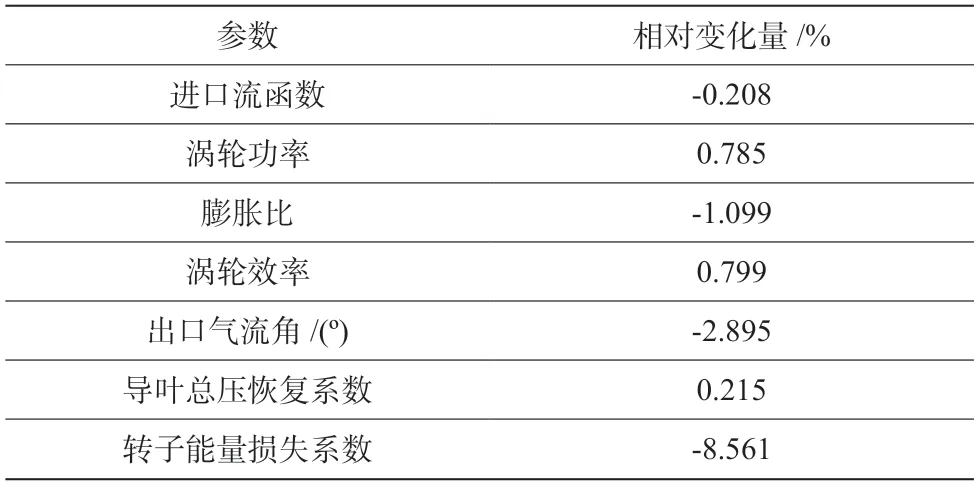
表2 优化前后涡轮性能对比Table 2 Performance comparison of the turbine before and after optimization

图6 控制点ts1 随优化步数的变化Fig.6 The convergence history of ts1

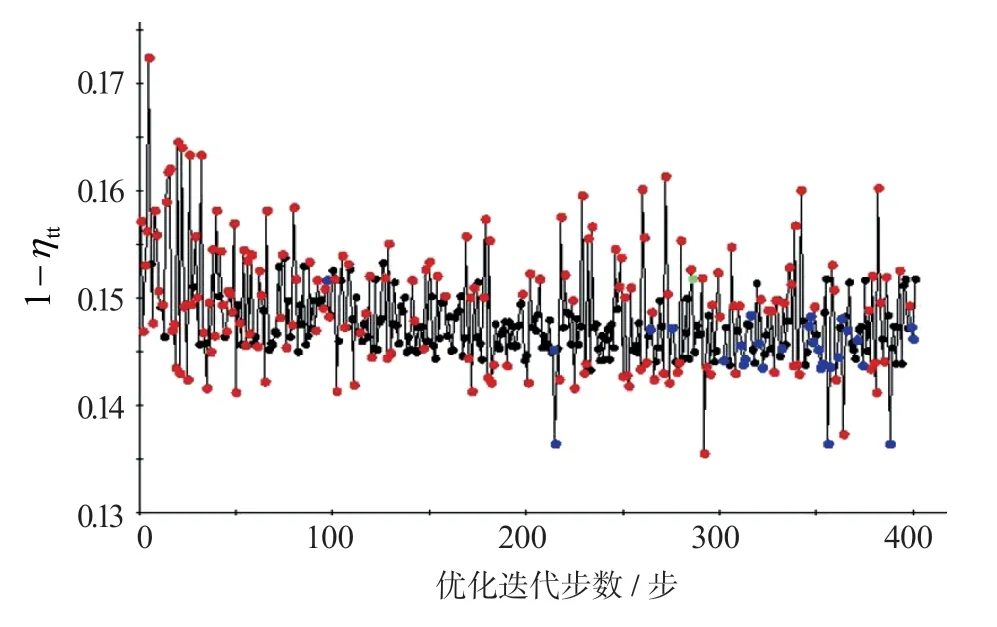
图7 1−ηtt 随优化步数的变化Fig.7 The convergence history of turbine efficiency

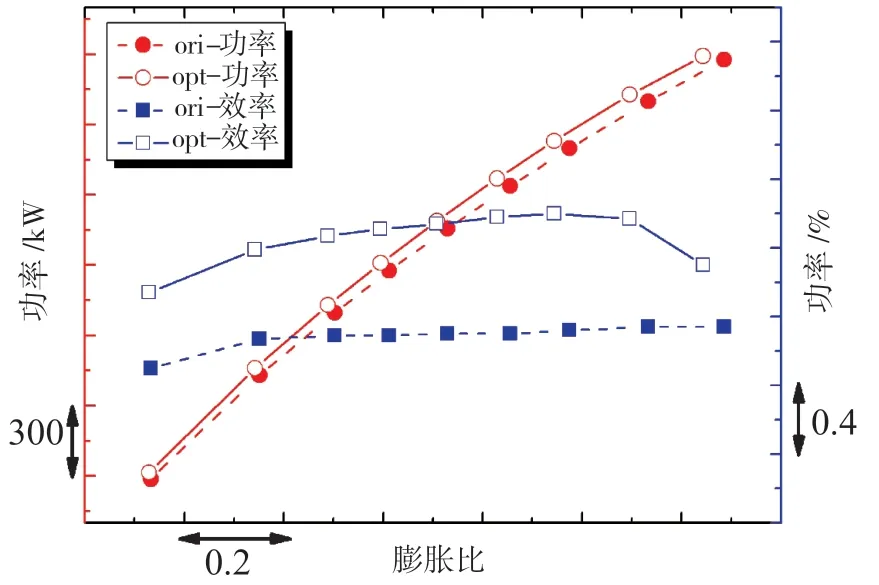
图8 优化前后不同膨胀比下涡轮效率和功率的变化趋势Fig.8 Comparison of efficiency and power of the turbine before and after optimization

图9 和表3 分别给出了优化前后2%、50%、98%叶高截面叶型和造型参数的对比。可以看到，优化前后，叶型前缘半径、厚度、尾缘楔形角与原型基本一致，为冷却叶片的设计提供了较好保障；从出口构造角上看，优化后叶根和叶尖截面相对原型分别“关小”了2.47°和8.53°；从进口构造角上看，优化后叶根截面和叶中截面相对原型增加了约3°，叶尖截面则基本保持不变。

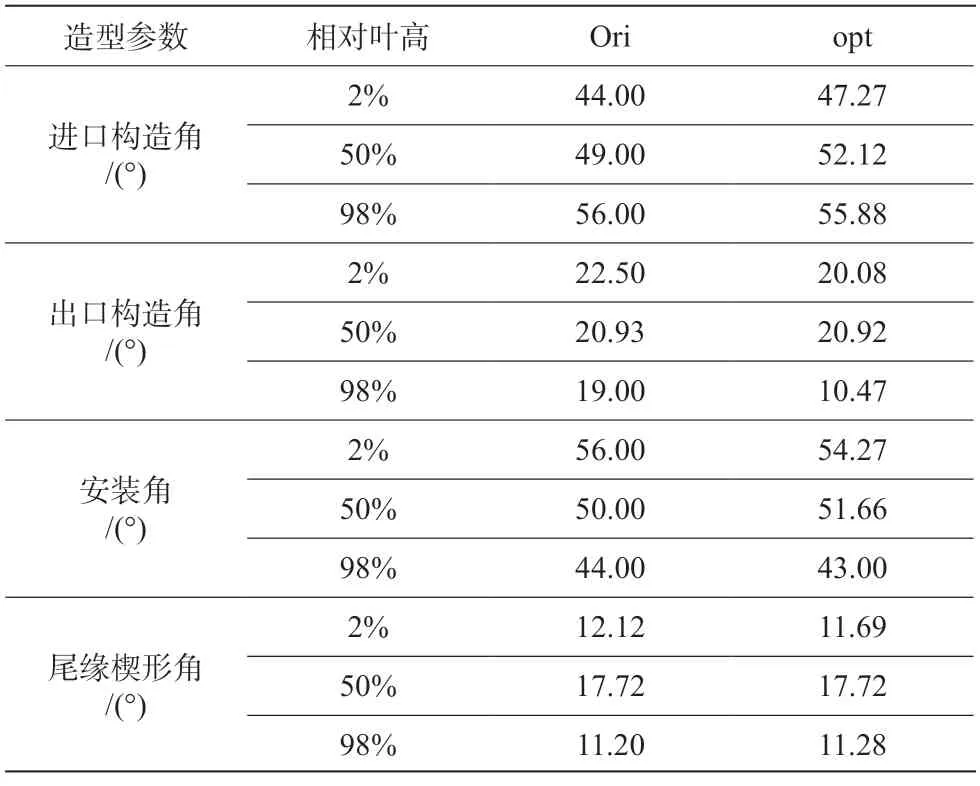
表3 优化前后造型参数对比Table 3 Comparison of blade parameters before and after optimization

图9 不同叶高叶型对比(黑：优化后；红：原型)Fig.9 Comparison of the blade at different span before and after optimization (black: opt;red: ori)

图10 给出了优化前后10%、50%、90%叶高截面叶型等熵马赫数(Mais)分布。可见，优化后吸力面前缘的吸力峰得到了明显削弱，气流从前缘加速到叶背更加自然；气流攻角得到了改善，叶片前缘区域负荷减轻，有利于降低马蹄涡压力侧分支的强度、减小损失。同时，吸力面尾缘处气流的加速状况也得到了改善。原型根、中、尖3 个截面吸力面的气流在80%轴向弦长后基本处于扩压状态，优化后气流持续加速到了约90%轴向弦长，速度峰值更加靠近尾缘，出口扩散段变短，扩散损失变小，这进一步减小了气流损失。此外，优化后叶片的总负荷有所降低，这必然减小叶栅通道间的横向压差，削弱通道涡的发展，对涡轮性能有益。

图10 不同叶高截面叶型等熵马赫数分布Fig.10 The distribution of isentropic Mach number at different span turbine before and after optimization

图11 给出了优化前后涡轮动叶表面极限流线和压力分布。可以看到，气流的正攻角状况有一定的改善，叶背上二次流影响范围和极限流线流向叶中的倾斜角度均有所减小，说明通道涡卷起的范围和强度均得到了抑制，有利于涡轮性能提升。

图11 叶片表面极限流线和压力分布Fig.11 Limiting streamline and pressure distribution on blade

图12、图13 分别给出了优化前后，转子叶片能量损失系数和反力度沿径向的分布。优化后，10%～80%叶高的能量损失系数小于原型，叶根和叶尖的能量损失系数则有所增加。这是由于优化后，叶中区域转子叶片的负荷减轻，前缘吸力峰减弱，攻角和尾缘处流动得到改善所致。优化后叶尖的反力度增加，导致叶尖间隙泄漏损失增大，使得80%叶高至叶顶的损失增加。综合叶片中部和端部的损失增量，优化后实现了效率的正收益。图14 给出了优化前后级出口绝对气流角的对比。可见，优化后叶片的横向压差减小，根部和尖部喉部面积缩小，反力度增加，出口气流马赫数增大，使得级出口绝对气流角较原型的偏离轴向更远。

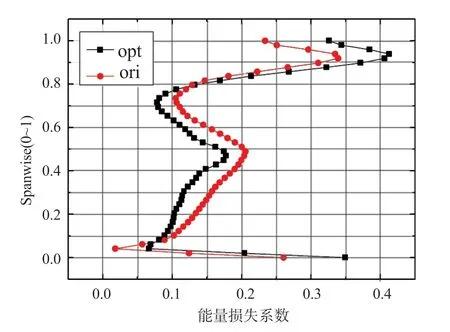
图12 优化前后能量损失系数径向分布Fig.12 Radial distribution of energy loss before and after optimization

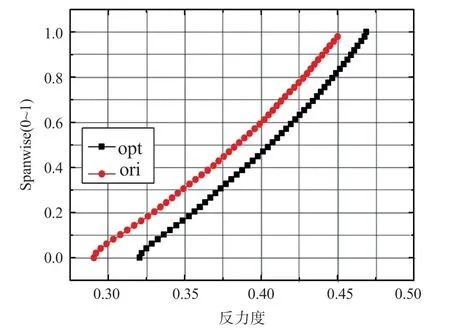
图13 优化前后反力度径向分布Fig.13 Radial distribution of reaction before and after optimization

图14 级出口绝对气流角径向分布Fig.14 Radial distribution of the stage outlet flow angle before and after optimization

4 结论

针对发动机高压涡轮气动性能提升需求，在不改变子午流道几何，并考虑叶片冷却、结构强度设计及与下游低压涡轮匹配的约束条件下，对其进行了级环境下的气动优化。主要结论为：

(1)对于所优化的高压涡轮，在保持进口流函数和反力度基本不变的条件下，效率随着轴向间距的增加先增大后减小。对于本次研究的涡轮，存在一个最佳的转静轴向间距(为导叶轴向宽度的0.3倍)，使得涡轮效率最高，较原型提高约0.2%。

(2)结合轴向间距和动叶进行了多目标优化，在保持涡轮进口流函数基本不变的条件下，涡轮的效率提高了0.799%，功率增加了0.785%，级出口气流角仅减小了2.3°，优化效果较好。

(3)基于iSIGHT，集成Numeca、CFX 软件，开发了三维气动优化集成平台，实现了叶型参数化、网格划分、数值计算及三维计算结果的自动处理与优化。实践证实，该平台在工程上具有良好的可行性与鲁棒性。