基于ALSTM的光伏出力短期预测研究

韩 坤

（中国大唐集团科学技术研究总院有限公司，北京 100040）

0 引言

随着全球对环境问题的关注，开发诸如风能[1]、水能[2]、燃料电池[3]、光伏[4]等可再生能源已成为普遍共识。国际能源署（International Energy Agency，IEA）评估，到2040 年，新能源的比例将达到60%，其中光伏和风能将占50%以上。光伏，即太阳能光伏，自1992 年以来，已从小规模应用的利基市场发展成为主流电源。2017 年，全球累计光伏发电量达到近460TWh，约占全球总能源的2%，其中60%用于公用事业的应用，其余40%用于分布式应用[5]。到2018 年底，全球累计光伏总容量达到512 千瓦，满足了全球2.55%的电力需求[6]。

但是，由于环境温度、相对湿度、风速和晴空指数等气象因素[7]，光伏发电具备间歇性的特性，会有相当大的波动性。在文献[8]中使用了神经网络来验证光伏功率输出与温度、风速和相对湿度密切相关性，文献[9]则证明了晴空指数和温度对光伏功率输出的性能有很大的影响。由于光伏发电输出受气象因素影响很大，强波动和间歇性会对电力系统运行和并网造成很大影响。当光伏大规模并网时，可能会引起电网振荡[10]。因此，准确预测光伏出力可以显著改善电力系统的运行，增加光伏系统的渗透率。

光伏功率预测的方法可概括为物理方法、直接预测方法和间接预测方法。物理方法主要依赖于从太阳能到电能的能量转换的理论分析获得的物理模型，物理模型通常基于数值天气预报、卫星图像和云运动模型[11]，这些模型可以高精度地预测光伏功率输出[12]。但是，这种预测方法需要卫星云图上的额外信息，导致更高的运行成本和计算成本。为解决此问题，直接预测方法，即时间序列方法被广泛应用于光伏预测。这些方法根据光伏功率序列的周期性、趋势性和其他特性，在历史功率序列和未来光伏功率之间建立数学关系。但是，这种方法缺少辐射、温度、湿度、风速和风向等气象信息，不完整的天气信息难以保证预测的准确性。为了提高预测精度，提出了间接预测方法，即回归方法。考虑气象因素后，某一时段光伏发电量的预测性能有了显著提高。间接预测方法包括人工神经网络[13,14]、支持向量机[15]和马尔可夫链[16]等。

本文通过深度学习方法，在基于MIE 构建的光伏特征输入基础上，利用ALSTM 的预测优势，采用回归方法对光伏出力进行了较为准确的短期预测。

1 ALSTM深度网络

1.1 长短期记忆网络（LSTM）

LSTM 是目前机器学习领域中广泛使用的深度学习方 法，由Hochreiter 和Schmidhuber 在1997 年 提出[17]。LSTM 是专门用于处理时间序列数据的深度学习模型，其在网络模型中加入门控制器，可以解决RNN 中的长期依赖问题（梯度爆炸或消失），结构如图1 所示。

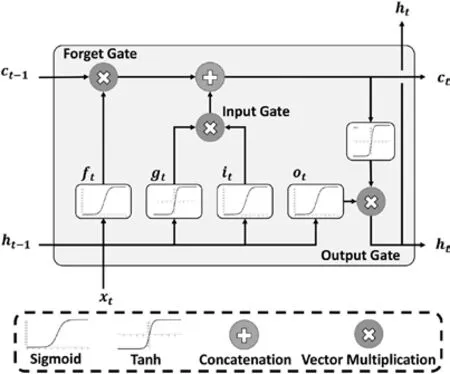
图1 LSTM网络结构Fig.1 LSTM Network structure

LSTM 模型在原有的短期记忆单元ht的基础上，增加一个记忆单元ct来保持长期记忆，同时增加3 个门控机制来控制整个学习过程中的信息流。LSTM 单元在每个时间步长t的状态被定义为一组5 个向量Rd：输入门it、遗忘门ft、输出门ot、隐藏状态ht和存储单元ct，d是LSTM 单位的数量。LSTM 传递函数为：

其中，xt是当前输入；σ表示sigmoid 函数；W和b是权重和偏置参数。遗忘门控制从存储单元删除不需要的信息，而输入门控制向存储单元添加新信息，输出门控制内部存储状态的暴露。通过3 个门，存储单元ct可以选择性地更新、删除和遗忘内部信息，从而更好地理解序列中的长期依赖性，提取时序数据中隐藏的特征。

1.2 注意力机制（Attention）

当神经网络接收到大量的输入信息输入时，不同的输入对输出值的影响是不同的。为提高神经网络的计算效率，对于相同的输出，更多的计算能力被分配给重要的输入信息，这种措施被称为注意力机制。

注意力机制分两步计算，第一步是计算所有输入值上的注意力分布值αi；第二步是计算单个输出值下的输入信息加权平均值。注意力机制如图2 所示。

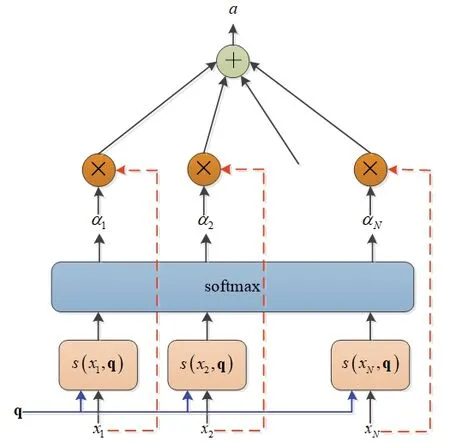
图2 注意力机制结构图Fig.2 Structure diagram of attention mechanism

其中，xi是输入值；q是神经网络的查询向量；s是注意力的得分函数；αi是查询向量q在所有输入值上的注意力分布值。

得分函数为：

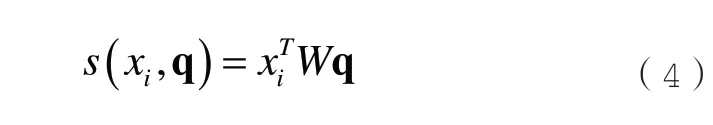
其中，W是可以自主学习的神经网络参数。计算式（4）的softmax 值，可以得到注意力分布αi，如式（5）所示：

a是注意力分布值α和输入值xi的加权平均值，表示为：

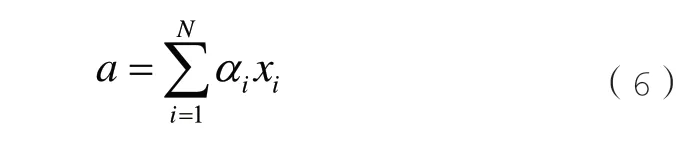
2 基于ALSTM的光伏短期功率预测

2.1 基于互信息熵(MIE)的相关性衡量

互信息为信息论中用来度量变量间信息共享程度的方式，它可以表征一个随机变量与另一个随机变量信息的相关性情况[18,19]。

定义向量X=[x1，x2，，，xn]，n为X的长度。如式（7）所示对X进行归一化计算：

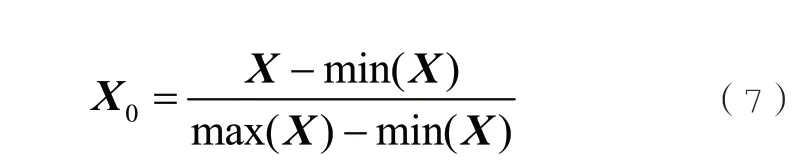
式（7）中，X0是X归一化处理后的结果。

设B为X0的组距，Ei为X0的波动区间上下限，其计算公式分别如式（8）和式（9）所示：

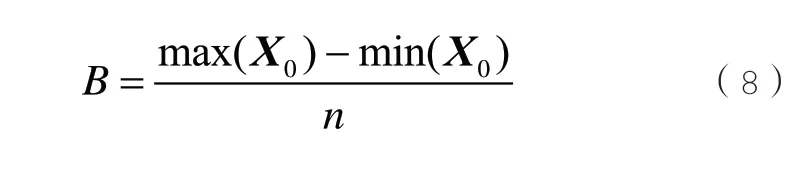
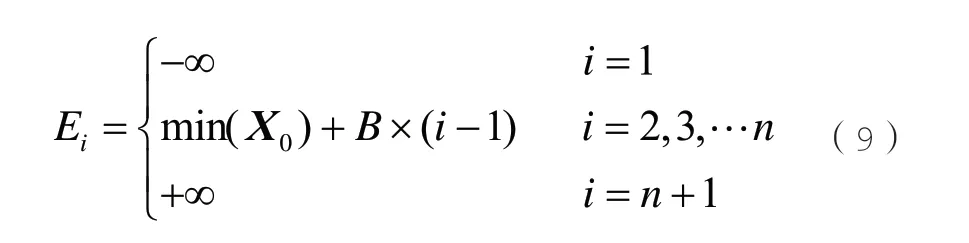
依据一维直方图分析法，按式（9）将X0分为n个波动区间，设Xi表示第i个波动区间，如式（10）所示：

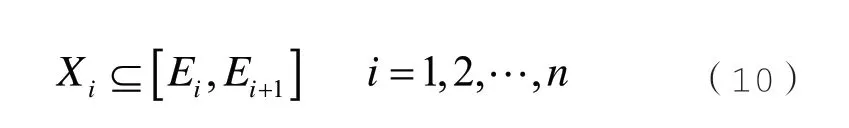
设p(·)表示上下限概率密度函数，则各波动区间Xi的上下限概率密度p(Xi)为：

式（11）中，ni为X0中元素在波动区间Xi的数据样本数。

通过自信息熵H(Xi)来表征X自身随机波动的不确定度大小，即：

依据香农信息论[15]，一维向量的自信息熵H(Xi)扩展到二维向量的互信息I(X;Y)，即为：

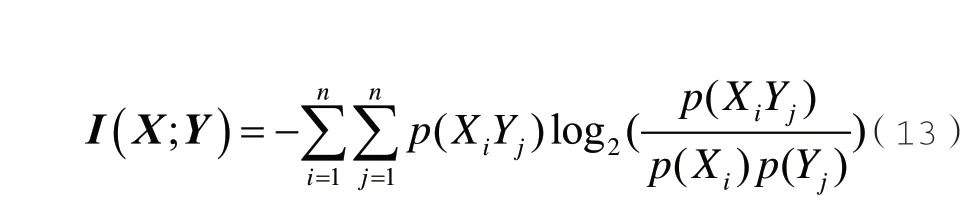
式（13）中，Y为与X不同的向量；p(Yj)为波动区间Yj的上下限概率密度；p(XiYj)表示X0和Y0在波动区间Xi和Yj的联合概率密度。

I(X;Y)表征了X和Y信息的共享程度，可用于衡量两个变量中一个同另一个相关性的大小情况。若向量X和向量Y彼此独立无关，那么向量X将不会给向量Y提供任何信息，它们彼此间的互信息为零；反之，若向量X和向量Y互相相关，则X和Y之间所传递的全部信息都会共享，那么二者间的互信息I(X;Y)=1。

为消除量纲的影响，广义互信息I(X;Y)经过归一化计算后，最终得MIE 相关系数IXY为：

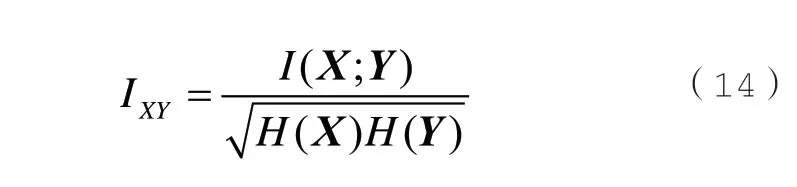
式（14）中，H(Y)表示向量Y的自信息熵。

MIE 表征了变量之间概率分布的统计特性，其始终是非负的，即IXY≥0，与广义的线性相关系数相关，可应用的范围更广，能更好地挖掘气象因素与光伏功率间的非线性相关性，有利于关键气象特征的筛选。

2.2 光伏特征输入选取

通过维度较大的数值天气预报（uNmerical Weather Forecast，NWP）气象数据进行光伏功率预测之前，要先对复杂气象输入数据与光伏功率输出数据进行关联性分析。要将与光伏功率相关性低的变量进行剔除，也即减少预测模型的噪声输入，对输入气象数据降维，提高预测模型精度的同时，也提升预测模型的运行效率。

若各气象变量Xi(i=1，2，…，5)分别为辐照度、温度、云量、风速和湿度，光伏功率则以变量Y表示。通过利用2.1 小节公式分别计算各输入气象因素与输出光伏功率的互信息熵（MIE）相关系数IXY=[IFP，ITP，ICP，IWP，IHP]，其计算结果见表1。

表1 气象因素和光伏功率的MIE相关系数Table 1 MIE correlation coefficients between meteorological factors and photovoltaic power

从表1 可知，各气象因素与光伏功率的MIE 相关系数由大到小分别是照度、温度、湿度、风速和云量，即辐照度和温度与光伏功率相关性最高，均大于0.9。为了最大程度地平衡训练精度和训练效率的关系，本文最终将MIE相关系数较高的前3 种气象因素，辐照度、温度及湿度作为光伏功率ALSTM 预测模型最终的输入变量，同时前一时刻光伏功率与当前时刻功率亦是强相关的，因此本文也将前一时刻的光伏功率送入预测模型。

2.3 预测误差指标

好的预测误差指标有助于预测模型更好的迭代寻优，也可方便进行不同算法之间的对比，本文选取常见的均方根误差和平均绝对误差作为预测误差指标，具体定义如下：

1）均方根误差

2）平均绝对误差

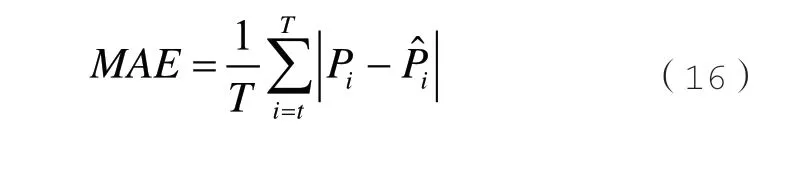
式中：T为的采样时间点数；Pi和分别代表i时刻实际值和预测功率值。

3 仿真验证

3.1 数据集

本文数据集取自澳大利亚布里斯班昆士兰大学露西亚校区的平板光伏系统的昆士兰大学中心（UQ Centre），该楼布置在建筑物屋顶的1806 块多晶硅太阳能电池构成，装机容量为433.44 kW[20]，如图3 所示。原始数据集是2012 年～2013 年完整的2a一 每天24h 和1min 采样周期的数据一因为光伏功率具有间歇性的特性，所以本文数据集实际只提取每天07:00～18:00 时间段的功率数据，从而原始的功率数据集包括481800 个采样点的数据（2a×365d×11h×60min），其中缺失了5034 个数据，占总数据的百分之一左右，本文通过向前平均法进行缺失数据的填充处理。

图3 昆士兰大学中心（UQ Centre）光伏系统Fig.3 University of Queensland Center (UQ Centre) photovoltaic system

为了平衡数据量和数据自身特征的保留情况，本文对原1min 采样周期的原始数据进行了重采样，每15min 提取一个数据，遇到缺失数据，则通过向前15 个数据平均替代，使预测时间尺度由1min 调整为15min，最终的光伏功率数据点总数为32320（15min）。

3.2 预测效果

为了验证本文所提ALSTM 预测模型的有效性和优越性，本文在昆士兰大学中心光伏数据集上，分别进行了晴天功率预测、阴雨功率预测以及天气剧烈波动日预测，同时还将双向LSTM（BiLSTM）和卷积神经网络（CNN）进行对比验证。

◇晴天数据预测

以2013 年6 月某天晴为预测数据样本，通过ALSTM预测模型进行预测。预测曲线如图4 所示。从图4 可知，晴天天气条件下，总体的光伏功率波动均较小，由表2 的RMSE 和MAE 预测误差指标值可知，ALSLTM 比BiLSTM和CNN 的预测误差更小。

图4 天晴日光伏功率确定性预测Fig.4 Deterministic prediction of photovoltaic power on sunny days

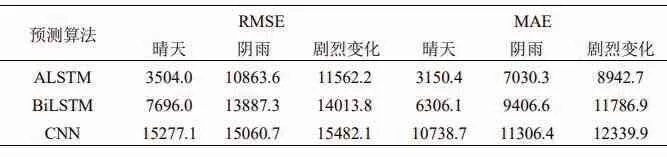
表2 光伏功率预测对比Table 2 Comparison of photovoltaic power predictions

◇阴雨天数据预测

为验证本文提出的ALSTM 预测模型在其他气象条件下的预测精度情况，选取6 月某一阴雨天作为光伏功率预测数据样本进行预测。预测结果如图5 所示。从图5 可知，阴雨天气下，光伏功率相比晴天整体波动要大。从表2 的两个误差指标可知，与另外两种深度学习算法预测结果相比，本文方法预测精度更高。

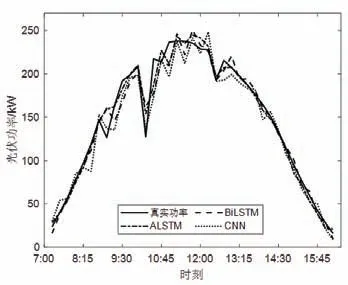
图5 阴雨天光伏功率确定性预测Fig.5 Deterministic prediction of photovoltaic power in cloudy and rainy days

◇复杂强波动天气数据预测

一个预测模型的好坏取决于其可否很好地在恶劣天气情况下，进行光伏功率预测。为验证本文提出ALSTM 在复杂强波动天气下的光伏功率预测情况，选取6 月某一强波动数据样本进行功率预测，预测结果如图6 所示。结合图6 以及表2 两个预测误差指标可知，复杂强波动天气下的光伏功率波动比阴雨天更大，但ALSTM 预测误差相对较小。与另外两种方法相比，精度更高，能更好地进行光伏功率预测，体现了本文ALSTM 预测模型的优越性和强鲁棒性。

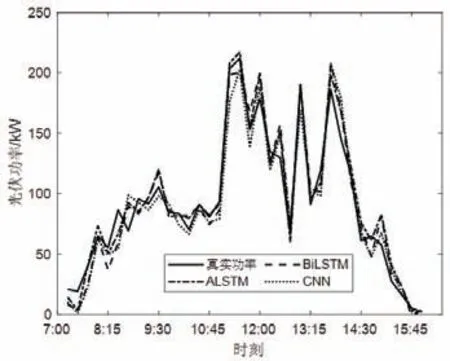
图6 天气剧烈变化日光伏功率确定性预测Fig.6 Deterministic prediction of photovoltaic power on days with severe weather changes

4 结论

准确可靠的光伏出力预测对改善电力系统运行能起到很大作用。本文基于LSTM 提取时序数据关联特征的优势，以注意力机制进一步改善LSTM 网络，构建了ALSTM 预测模型，通过MIE 方法衍生光伏特征输入，对影响光伏功率预测的复杂气象因素进行降维处理，进一步减少输入噪声和提示预测精度。在昆士兰大学中心光伏出力数据上，通过天晴、阴雨天以及天气剧烈波动日的光伏功率预测情况，并与BiLSTM 和CNN 的对比验证可知，ALSTM 能更准确地在晴天、阴雨天以及天气剧烈波动日等情况下进行光伏出力预测，具有更好的鲁棒性和适用性。