基于改进深度ResBiLSTM的短期风电功率预测

路 岩

（中国大唐集团科学技术研究总院有限公司，北京 100040）

0 引言

对可持续环境和能源系统的日益关注使太阳能和风能等可再生能源得到广泛增长，使发电组合构成发生了显著变化[1,2]。这些资源的最高年增长率可以在世界各地观察到，可从中看出能源结构的快速转变[3]。例如，全球风力发电能力从2010 年的180 千兆瓦增长到2019 年的622千兆瓦，太阳能发电能力同时从41 千兆瓦增长到585千兆瓦[4]。由于太阳能和风能的经济效益提高，预计其渗透率将进一步增长。但是，风电等新能源与天气的强相关性会威胁电力系统运行的可靠性和经济性[5]，导致重大的社会和经济损失[6]。因此，准确的风电功率预测，有助于电网的安全和经济运行。

风电功率预测方法可分为3 类：物理方法、常规统计方法和基于人工神经网络的方法。物理方法建立在中尺度天气模型或数值天气预报系统的基础上，它代表了基于各种地理和气象信息的数学表达模型[7,8]。虽然这种方法对3 h 以上的中期预报效果很好，但它对短期预报有局限性，因为很难收集所有相关的地理或气象数据[9-11]。传统的统计方法是基于历史数据产生风力输出的线性特征，如自回归模型或ARIMA 模型已被广泛用于构建线性关系。但是，风电数据的非线性往往会损害模型的准确性和通用性。尽管基于传统统计方法有各种方法来表示非线性，但这些基于线性形式的方法在表示非线性动力学方面仍然受到限制[12-14]。而基于人工神经网络的方法，则可以有效地表示风速和功率的非线性和复杂特征，因此基于人工神经网络的风电功率预测或风速预测模型比物理或常规统计方法具有更高的精度[15,16]。与此同时，除了这3 种方法，有研究提出了混合模型，将基本人工神经网络模型与其他模型（如卡尔曼滤波器和支持向量机）并行，以提高风电功率预测的精度[17,18]。在深度神经网络（DNN）中引入循环神 经网络（RNN）提高了人工神经网络模型的精度[19,20]。基于长期保存数据的能力，LSTM 被用于提取风电功率时序数据的时间特征[21]。如文献[22]所述，基于LSTM 的风电功率预测模型优于基于人工神经网络或ARIMA 的模型。

本文为解决风电功率预测的难题，从网络结构以及网络深度两方出发，通过融合网络方法构建了改进的深度ResBiLSTM 网络，对风电短期功率进行了较为准确的预测。

1 深度残差BiLSTM网络模型

1.1 长短期记忆神经网络(LSTM)

LSTM 是传统RNN 的改进结构，以克服其在解决长期依赖问题上的局限性。LSTM 可以通过增加一个特殊的隐藏单元来缓解渐变消失的问题，该单元可以增加或删除新的输入。3 个控制门通过控制数据流来确定单元的操作，如图1 所示。遗忘门从状态向量中丢弃无用的信息，输入门从新的输入和先前的净输出中添加必要的信息。最后，相应单元的新输出由输出门决定。基于这些操作，LSTM 单元可以长时间保存有用的数据，因此它比传统的RNN 更好地捕捉长期相关性。

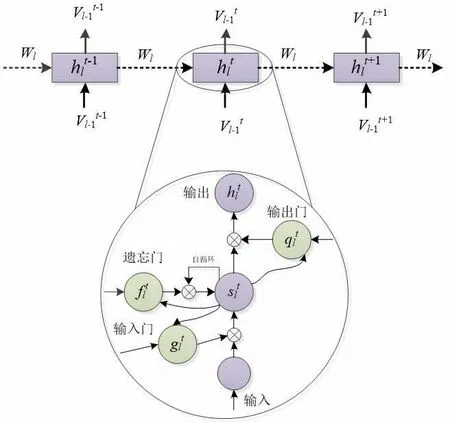
图1 LSTM单元结构Fig.1 LSTM unit structure

双向学习有助于提高传统LSTM 的准确性[12]。双向LSTM（BiLSTM）通过正向和反向路径训练其参数来理解上下文，这个训练过程可以捕获双向方面的特征或模式，而LSTM 只在前向路径中训练。BiLSTM 在序列学习中表现出比传统RNN 更高的准确性和性能。如图2 所示，BiLSTM 将双向概念引入LSTM。BiLSTM 的前向层像LSTM 网络一样，更新单元中的参数。另一方面，后向层中的LSTM 单元计算前向层中传播误差的导数。后向层中单个LSTM 单元h 的操作可以描述如下：

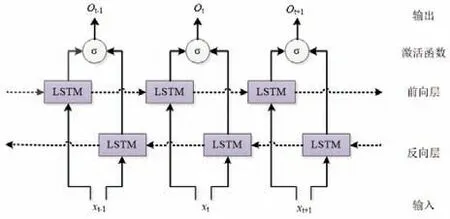
图2 双向LSTM网络的总体结构Fig.2 The overall structure of the bidirectional LSTM network

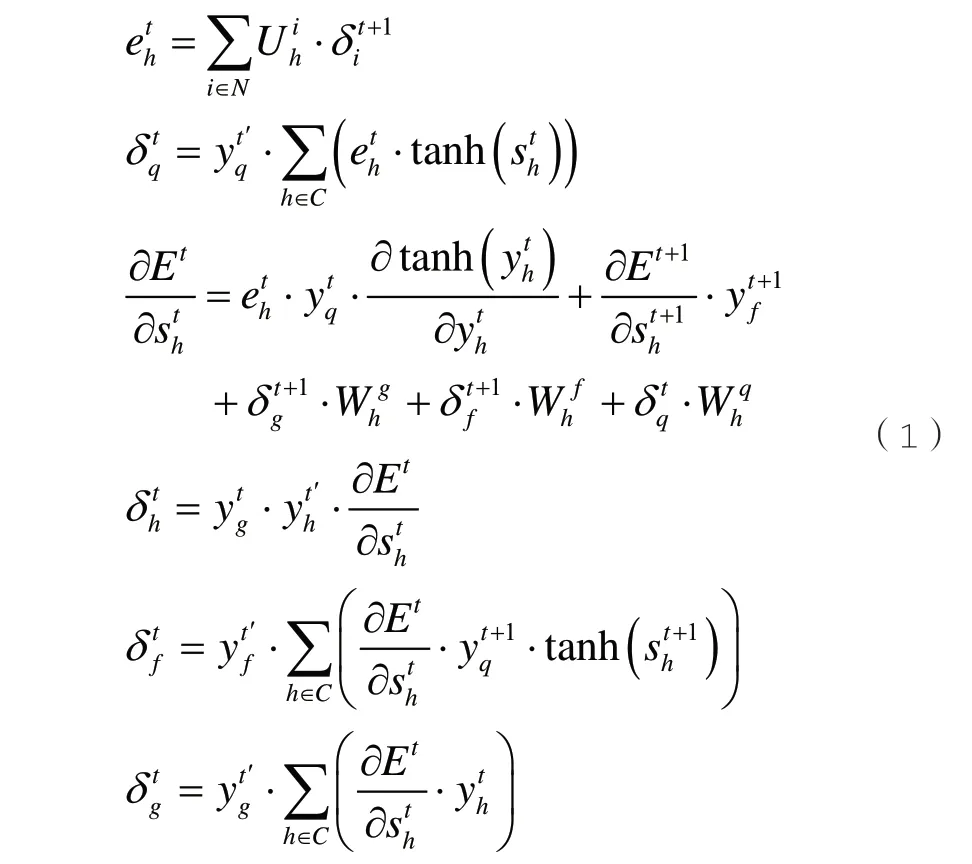
1.2 残差BiLSTM网络

He 等[13]提出了残差网络结构（ResNet），通过引入残差块（Residual block）来构建深度网络。残差块以x 为输入，H(x)为输出，结构如图3 所示。其中，F(x)为残差映射函数。

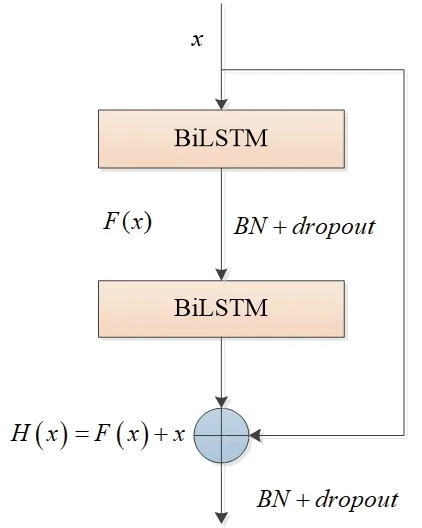
图3 残差块结构图Fig.3 Residual block structure diagram

构建深层网络的基本约束是堆叠后的网络模型误差应不高于基础的浅层模型，He 等在实际中采用恒等映射的方法构建深层模型，即用H(x)=x 表示一组堆叠网络层的最佳解映射。当网络较深时，模型难以直接拟合实际映射H(x)，残差网络通过引入“shortcut”快捷连接将问题转换为拟合残差映射F(x)，此时实际映射H(x)表示为H(x)=F(x)+x。当F(x)=0 时，就构成了一个恒等映射H(x)=x，模型只需最小化残差函数F(x)=H(x)-x 来逼近实际映射，以解决网络层堆叠的性能退化问题。

常规的深度残差网络即将图3 所示残差块层层堆叠，但不管堆叠多少层，均能够维持输入流，不会卡在某些训练细节上，因此可以防止网络的过拟合或者梯度爆炸等情况。

1.3 改进的深度残差BiLSTM网络

为进一步提高网络的准确性，本文通过融合网络方式改进了深层残差网络，融合网络包括垂直和水平方向的堆叠层，其中水平方向的堆叠并非简单相加，而是将各级网络进行合并串联连接起来，充分利用各级网络特征提取能力，具体的网络形式如图4 所示。

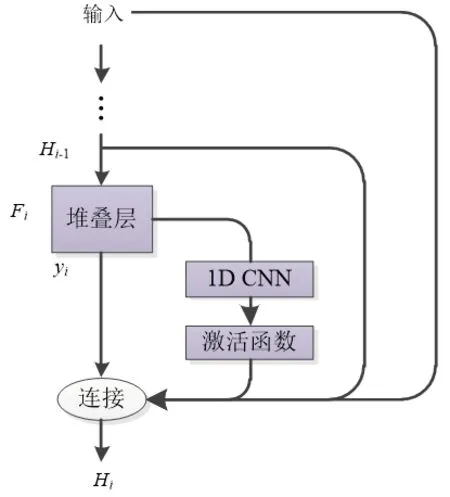
图4 融合网络结构Fig.4 Fusion network structure

本文的水平堆叠映射采用1D CNN 方式，可以进一步提取数据时间特征。

2 基于深度残差BiLSTM的功率预测

2.1 基于互信息熵(MIE)的相关性衡量

互信息为信息论中用来度量变量间信息共享程度的方式，它可以表征一个随机变量与另一个随机变量信息的相关性情况[18,19]。

定义向量X=[x1，x2，，，xn]，n为X的长度。如式（2）所示对X进行归一化计算：

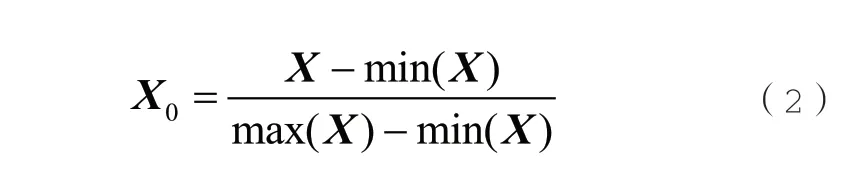
式（2）中，X0是X归一化处理后的结果。

设B为X0的组距，Ei为X0的波动区间上下限，其计算公式分别如式（3）和式（4）所示：

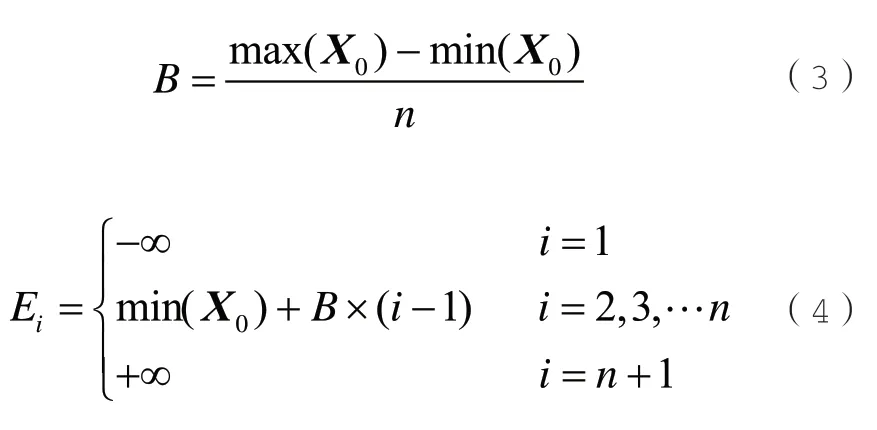
依据一维直方图分析法，按式（4）将X0分为n个波动区间，设Xi表示第i个波动区间，如式（5）所示：

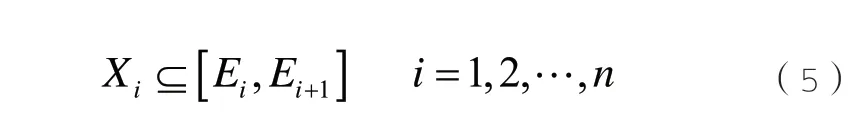
设p(·)表示上下限概率密度函数，则各波动区间Xi的上下限概率密度p(Xi)为：

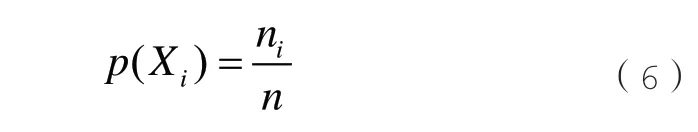
式（6）中，ni为X0中元素在波动区间Xi的数据样本数。

通过自信息熵H(Xi)来表征X自身随机波动的不确定度大小，即：

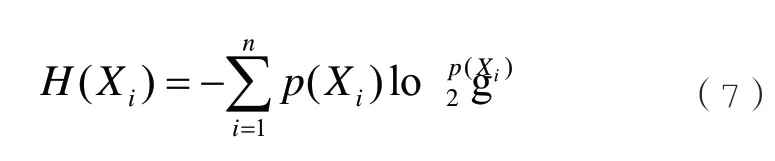
依据香农信息论[15]，一维向量的自信息熵H(Xi)扩展到二维向量的互信息I(X;Y)，即为：

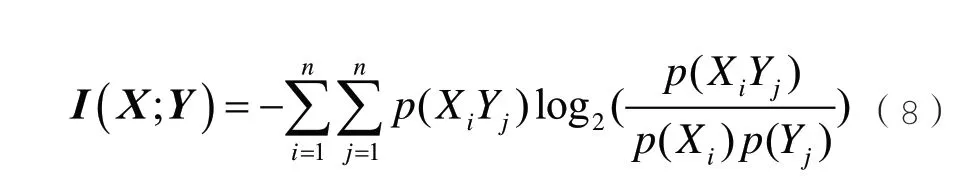
式（8）中，Y为与X不同的向量；p(Yj)为波动区间Yj的上下限概率密度；p(XiYj)表示X0和Y0在波动区间Xi和Yj的联合概率密度。

I(X;Y)表征了X和Y信息的共享程度，可用于衡量两个变量中一个同另一个相关性的大小情况。若向量X和向量Y彼此独立无关，那么向量X将不会给向量Y提供任何信息，它们彼此间的互信息为零；反之，若向量X和向量Y互相相关，则X和Y之间所传递的全部信息都会共享，那么二者间的互信息I(X;Y)=1。

为消除量纲的影响，广义互信息I(X;Y)经过归一化计算后，最终得MIE 相关系数IXY为：

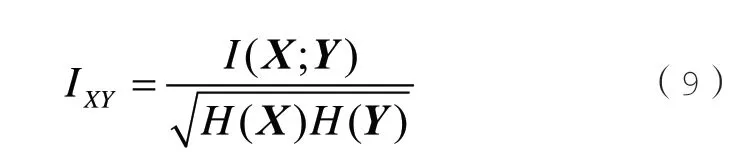
式（9）中，H(Y)表示向量Y的自信息熵。

MIE 表征了变量之间概率分布的统计特性，其始终是非负的，即IXY≥0，与广义的线性相关系数相关，可应用的范围更广，能更好地挖掘气象因素与光伏功率间的非线性相关性，有利于关键气象特征的筛选。

2.2 风电特征输入选取

为降低预测难度，需减少预测输入中与风电功率低相关因素的干扰，因此需要简化预测输入特征变量，从而减低输入维度。假设各气象变量X'(i=1，2，…，4)分别代表风速、风向、温度和气压，风电功率表示为Y'。本文利用2.1 节中的公式分别计算各气象因素与风电功率的MIE 相关系数IXY'=[ISP，IDP，IEP，IPP]，其计算结果见表1。

表1 各气象因素与风电功率的MIE相关系数Table 1 MIE Correlation coefficients of various meteorological factors and wind power

从表1 可知，各气象因素与风电功率的MIE 相关系数由大到小分别是风速、风向、温度和气压，即风速和风向与风电功率相关性最高，均大于0.5。为了最大程度地平衡训练精度和训练效率的关系，本文最终将MIE 相关系数较高的前两种气象因素（风速和风向）作为风电功率深度ResBiLSTM 预测模型最终的输入变量，同时本文还将历史功率值亦作为输入变量之一。

2.3 预测误差指标

好的预测误差指标有助于预测模型更好的迭代寻优，也可方便进行不同算法之间的对比，本文选取常见的均方根误差和平均绝对误差作为预测误差指标，具体定义如下。

1）均方根误差

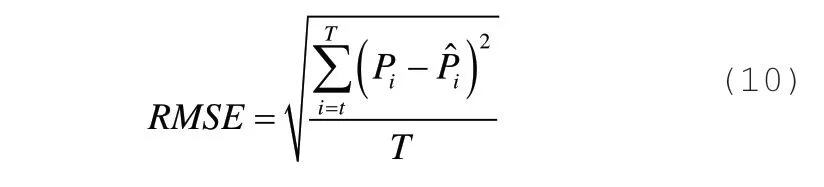
2）平均绝对误差

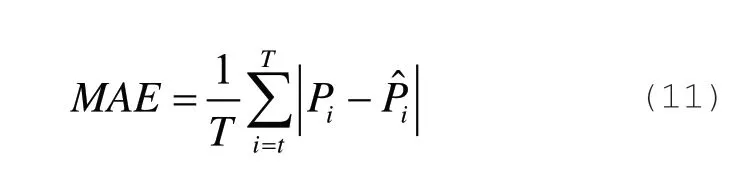
式中，T为采样时间点数；Pi和别代表i时刻实际值和预测功率值。

3 仿真验证

3.1 数据集

风力发电数据集取自2017 年～2019 年26311 h的ERCOT 每小时总风力输出[14]。数据显示了德克萨斯州所有风力发电机的总输出功率。总装机风力发电量从16246MW 增加到22607MW，最大风力输出为19099MW。本文先是建立了三层LSTM 风速和风向预测模型，根据风速和风向的历史值对当前风速和风向进行了预测。随后根据风速和风向的预测值，以及风功率的历史值，构建了深度ResBiLSTM 风功率预测模型。

3.2 预测效果

从图5 和图6 中可以看出，无论风速还是风向，二者的预测值和实际值趋势和大小基本一致，利用2.3 小结的平均绝对误差公式进行计算，得到二者平均绝对误差分别为3.54 m/s 和21.7°，可见均较小，预测效果良好。

◇风速预测

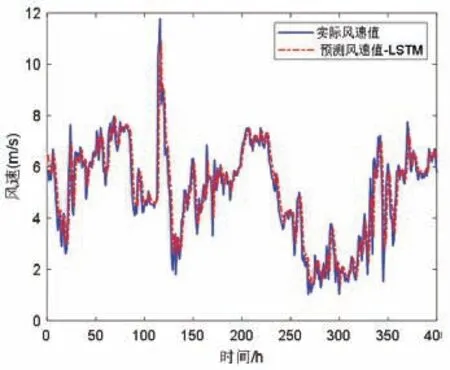
图5 风速预测Fig.5 Wind speed prediction

◇风向预测

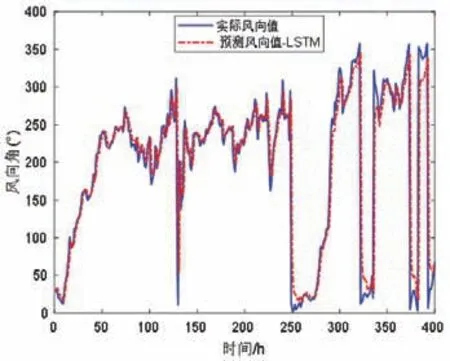
图6 风向预测Fig.6 Wind direction forecast

◇风电功率预测

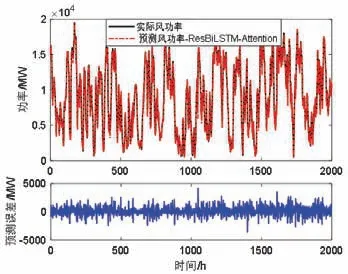
图7 风功率预测Fig.7 Wind power prediction

◇预测对比

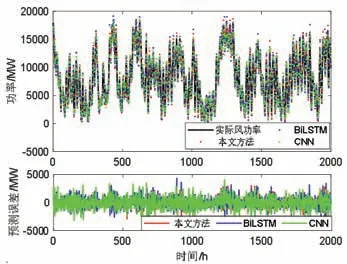
图8 风功率预测算法对比Fig.8 Comparison of wind power prediction algorithms

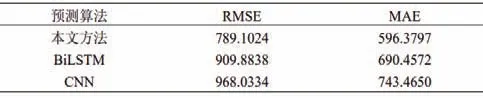
表2 预测结果比较Table 2 Comparison of prediction results

从图7 可知，本文算法的预测值与实际值较为接近，误差值在零附近波动，仅在个别点出现较大的误差。图8是本文算法与另外两种算法的对比验证情况，表是3 种算法的RMSE 和MAE 指标的计算结果，从表看出本文提出的算法RMSE 和MAE 两种误差均更小，可见本文所提预测模型可以更好地适应风电机组的实际工作条件，具有更高预测准确率。

4 结论

为更准确地进行短期风电功率预测，本文充分结合BiLSTM 的网络结构以及深度网络非线性表示的优势，以融合网络方法对ResBiSLTM 进行了改进，同时通过MIE方法对影响风电功率预测的气象因素进行降维处理，降低了输入的复杂性，提升了预测模型精度和效率。在ERCOT 风电厂与BiLSTM 和CNN 的对比验证可知，改进的ResBiLSTM 能更准确地进行短期风电功率预测。本方法针对复杂时序数据进行专门设计，亦可对其他时序数据进行准确预测，具有较大的可推广性。