回归分析拟合刮板取料机俯仰拉力曲线

孙伟哲 陈 玲 罗威强

中国交通信息科技集团有限公司 上海 200125

0 引言

刮板取料机普遍应用于电力、钢铁、码头等散货输送领域，其俯仰机构采用钢丝绳卷扬变频驱动，作业灵活、控制精准。钢丝绳拉力值通常作为刮板取料机运行保护的重要参数，但行业内对该参数的保护值确定较为简单，无法全面、准确地保护刮板取料机设备运行安全。

1 刮板取料机的结构

刮板取料机[1]作为一种高效取料设备，在条形、圆形等煤炭堆场的连续取料工艺中得到了日益广泛的应用。图1为刮板取料机实物图，刮板取料机本体一端通过钢丝绳吊挂在悬臂架上，另一端铰接至悬臂架下方。刮板机构驱动装置通过减速器联接至驱动轴，驱动轴通过链轮带动链条在悬臂架的支承下循环运转。固定在链条上的刮板随链条运动，将物料刮取到取料机落料斗。

图1 刮板取料机实物图

2 刮板取料机俯仰拉力保护的必要性

刮板取料机的俯仰[2]依靠钢丝绳卷扬机构实现，卷扬机构驱动采用变频调速电机，可通过调节钢丝绳伸出长度控制刮板每次下俯的幅度，进而调节取料层深。

刮板取料机主体为箱梁结构，长度较长、自重较大，正常作业工况下，不允许刮板取料机下方承受平整料堆之外的其他支撑力，即不允许出现钢丝绳拉力过小的情况，否则会造成刮板取料机箱梁结构变形等不利影响。

精确获取刮板取料机钢丝绳的拉力，能间接得知刮板取料机下方的承力大小，并依此对刮板取料机启动、下俯和行走制定程序逻辑限制，是全方位保护刮板取料机设备安全运行的有效手段。

3 刮板取料机钢丝绳拉力工况分析

刮板取料机主机制造厂通常会在俯仰机构左右两侧钢丝绳上各安装1个拉力传感器，图2为拉力传感器安装实物图。拉力传感器将钢丝绳拉力模拟量以DC 4～20 mA形式输出至刮板取料机PLC控制系统，在PLC控制系统内将其转换为实际拉力值，但制造厂出厂标准程序保护手段较为单一，通常情况是钢丝绳拉力小于特定数值即触发保护停机。这种保护方式简单机械，不能可靠、灵活、高效地保护刮板取料机在各种工况下的安全作业。

图2 拉力传感器安装实物图

实际刮板取料机在不同工况下，钢丝绳受力的情况也不同：

1）在刮板取料机悬空状态下，门架通过钢丝绳拉起整个刮板取料机，俯仰钢丝绳拉力值稳定。

2）悬空状态下，刮板取料机俯仰角度不同，俯仰钢丝绳拉力也不同。

3）在刮板取料机重载作业时，其下方承受了一定的来自平整料堆的支撑力，俯仰钢丝绳的拉力小于刮板取料机悬空状态时的值。

4）当刮板链条不运转而直接将刮板取料机放置在料堆上时，俯仰钢丝绳的拉力值要小于最小安全拉力的下限值。

综上所述，控制软件应将采集到的钢丝绳实时拉力与此时理论允许的空载、重载拉力值相比较。根据当前工况，输出相应的保护及联锁信号，实时保护刮板取料机的运行安全。实现拉力保护的关键由此转化为如何获取拉力值的理论曲线。

4 理论拉力曲线的获得步骤

如想获知刮板取料机在任意俯仰角度的理论拉力值，可按如下步骤实施（以空载拉力曲线为例）：

1）在空载情况下，在不同的俯仰角度采样，经过力学计算得到若干对应的拉力受限值。

2）建立平面直角坐标系，横坐标为刮板取料机俯仰角度，纵坐标为钢丝绳的拉力值，形成由几个散点组成的折线。

3）采用回归分析的数学方法，拟合一条曲线，尽可能地与上述散点图匹配起来。

4）将该曲线作为设计曲线，预测在任意倾角下刮板取料机的钢丝绳拉力空载受限值。

5 曲线拟合的回归分析[3]

5.1 数据分析并建立回归模型

选取如图3所示的刮板为测试对象，设计参数为：刮板取料机质量100 t，刮板长度53.5 m，吊点位置35.5 m，刮板俯仰角度范围-5°～45°，离俯仰铰点横向24 m，离俯仰铰点垂向27 m，边长36.12 m。

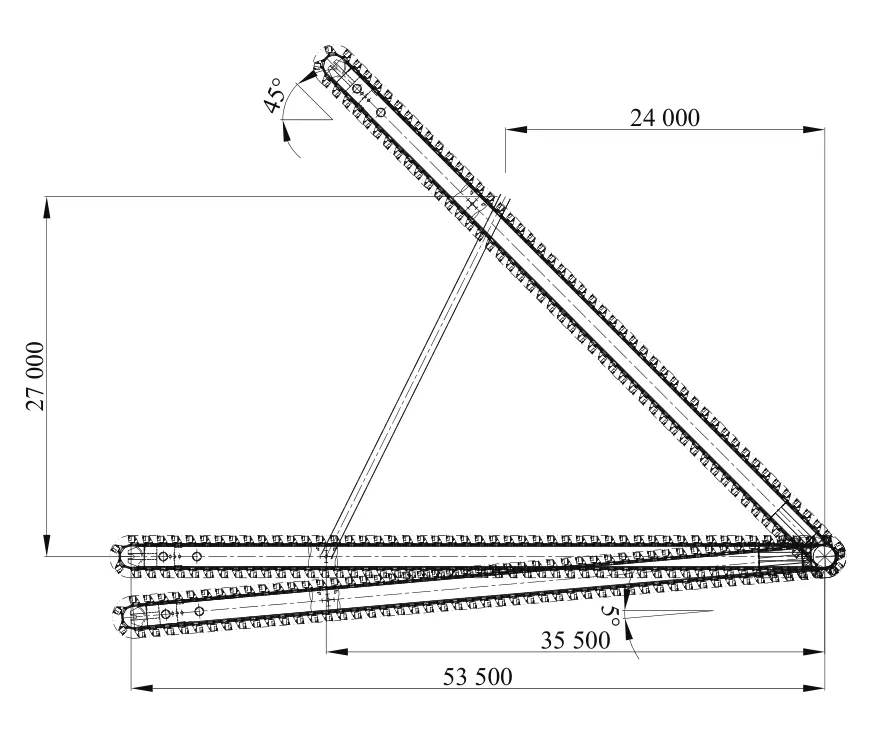
图3 刮板设计图

经过实际测量和力学计算，可得刮板取料机在空载工况下，刮板俯仰角度分别在0°、10°、20°、30°、40°所对应的拉力值，设x（刮板俯仰角度）为自变量，y（拉力值）为因变量，可得到5组散点坐标实测值（见表1），其中拉力为俯仰装置2根钢丝绳的拉力之和。

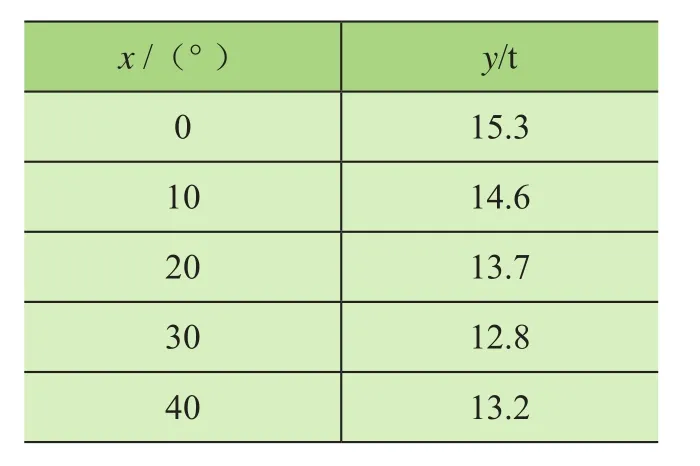
表1 拉力散点坐标实测值

根据表1建立x-y轴坐标系，将拉力散点坐标实测值标注在坐标图中，并将散点平滑连接，描绘出散点图，图4为采样拉力散点图。假设y与x之间存在某种线性关系，建立一元线性回归模型为

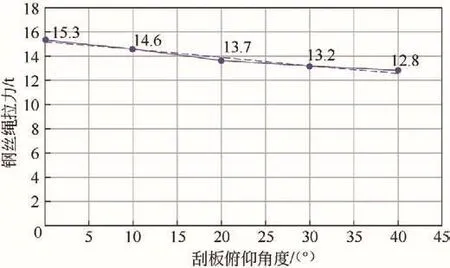
图4 采样拉力散点图

求得常数b0和b1，即可得到在空载工况下俯仰拉力值与俯仰角度的近似方程关系，进而得到在刮板俯仰范围内任意角度的俯仰拉力值。由于俯仰拉力值与俯仰角度不是绝对的线性关系，所以需采用回归分析的方式进行计算并验证b0和b1，使求得的一元线性线性方程曲线与实际曲线更加拟合。

5.2 估计参数

表2 计算值

5.3 曲线拟合程度与显著性检验

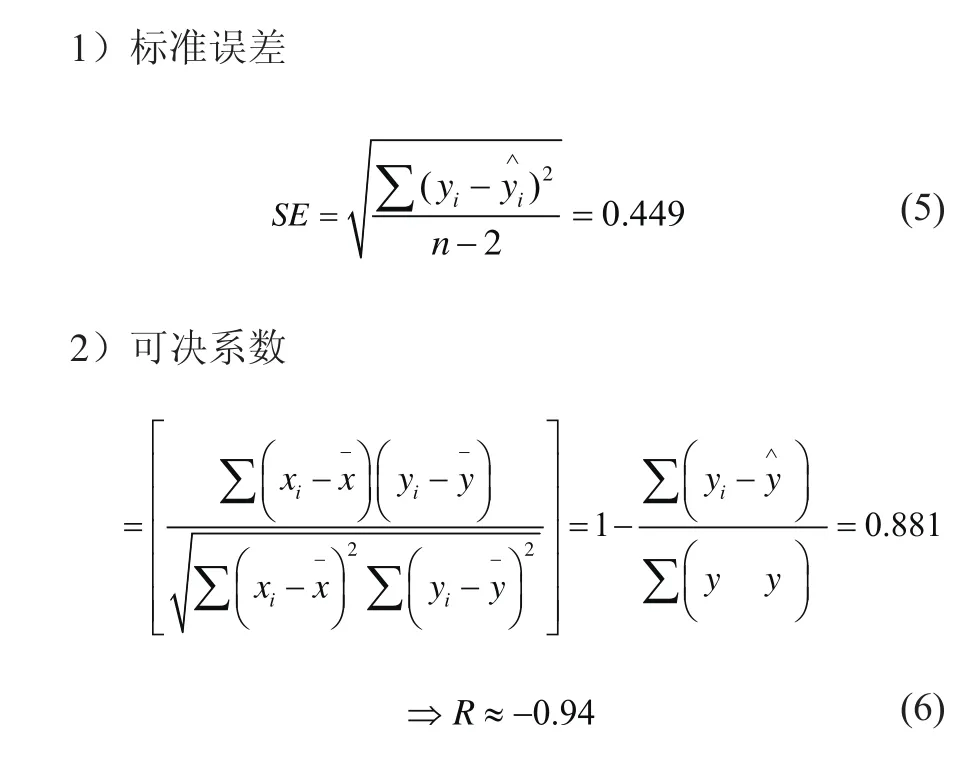
由此可以看出，自变量与因变量的拟合程度比较好。

3）回归系数显著性检验

4）回归模型的显著性检验假设

检验假设H0为回归方程显著，H1为回归方程不显著。

检验统计量

当α= 0 .05时，回归方程效果显著。

由上述回归分析与检验可以看出：可采用回归方程预测在给定倾角的情况下，空载时允许启动的钢丝绳拉力下限值。当且仅当钢丝绳测得的拉力值在预测值附近时，刮板取料机才允许启动。

同理可得重载极限时的预测回归方程。当钢丝绳的拉力小于重载极限值时，禁止刮板取料机启动、下俯以及行走。

6 结语

在大量刮板取料机的改造项目中，基于上述原理在控制软件中预设了刮板取料机俯仰钢丝绳拉力空载、重载保护理论曲线，作为安全检测子程序的数据依据，纳入刮板取料机运行保护逻辑中。实践证明，运行效果良好。