基于仿生算法优化的镜像极限学习机的应用*

印煜民，廖柏林

(吉首大学计算机科学与工程学院,湖南 吉首 416000)

反向传播训练神经网络是人工神经网络的一种，已广泛应用于现实生活中[1].然而这种传统的神经网络学习算法存在固有缺陷，需要设置大量的网络训练参数，且在迭代中收敛较慢[2].2004年，黄广斌等设计了一种名为极限学习机(Extreme Learning Machine，ELM)的单隐层前馈神经网络(Single-Hidden Layer Feed Forward Neural Network，SLFN)[3].

ELM在参数确定过程中无需任何迭代步骤，从而大大缩短了网络参数调整时间[4-8].与传统的训练方法相比，ELM具有学习速度快、泛化性能好的优点[9-10]，可以有效地应用于模式分类[11-14].值得指出的是，在确定参数时，所有ELM和类ELM神经网络模型都是随机生成输入层权值，然后计算输出层权值[15].为了设计一种分类准确率更高、网络结构更简单的类ELM网络模型，笔者拟提出一种新的权值确定方法，即交换输入权值和输出权值的确定顺序，并结合仿生算法进一步优化该方法的权值选择.

1 镜像权值确定极限学习机

1.1 极限学习机

如图1所示，ELM神经网络由3层组成，具有较简单的神经网络结构.其输入层和输出层分别有J和K个神经元，采用简单的线性激活函数；隐层有M个神经元，这些神经元被单调的非线性激活函数f(·)激活.连接第m个隐层神经元和第k个输出层神经元的权值用bmk(m=1,2,…,M；k=1,2,…,K)表示，输出权值bmk在(c1，c2)范围内随机生成；连接第j个输入层神经元和第m个隐层神经元的权值用ajm(j=1,2,…,J；m=1,2,…,M)表示，输入权值ajm由伪逆方法确定.在(c3，c4)范围内随机生成第m个隐层神经元的偏置hm，并将输入层和输出层中的偏移值设置为0，于是得到某个神经元的输出结果：

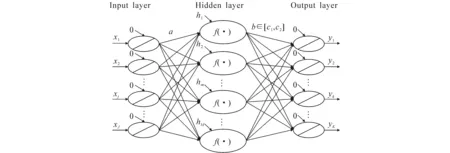
图1 极限学习机神经网络模型

(1)

其中xj表示第j个输入层神经元的输入.(1)式可以简写成

y=Bf(Ax-h).

(2)

其中：y=(y1,y2,…,yK)T∈RK×l；x=(x1,x2,…,xJ)T∈RJ×l；h=(h1,h2,…,hM)T∈RM×l；输出层权值矩阵B与输入层权值矩阵A分别定义为

1.2 镜像极限学习机权值的确定

本研究中改进的ELM的权值确定方式与传统的ELM权值确定方式互为镜像，即随机生成输出权值，随后通过伪逆计算的方式获得输入层权值，因此将改进的ELM称为镜像ELM(Mirror Extreme Learning Machine，MELM).

将实验样本数设置为N，可得(2)式矩阵形式的输出，

Y=Bf(AX-H).

(3)

其中：Y=(y1,y2,…,yN)T∈RK×N；X=(x1,x2,…,xN)T∈RJ×N；H表示隐层神经元的矩阵形式偏移量，H=(h,h,…,h)T∈RM×N.

定理1假设激活函数f(·)是严格单调的.当分别从[c1，c2]和[c3，c4]中选择输出权值B和偏差H时，最佳输入权值A=(f-1(B+Y)+H)X+，其中f-1(·)表示f(·)唯一的逆函数，B+和X+分别表示矩阵B和X的伪逆矩阵.

证明(3)式两边同乘以B+，得到

B+Y=B+Bf(AX-H)=f(AX-H).

(4)

求解(4)式的反函数，得到f-1(B+Y)=AX-H，将其继续改写为

AX=f-1(B+Y)+H.

(5)

在(5)式两侧右乘X+，得到AXX+=(f-1(B+Y)+H)X+，即A=(f-1(B+Y)+H)X+.证毕.

2 天牛须搜索算法

天牛须搜索(Beetle Antennae Search,BAS)算法[16]是一种高效的智能优化算法.天牛须搜索算法的生物原理为：天牛觅食时不知道食物的位置，但它会根据食物的气味强弱搜寻其位置.天牛有2只长触须，如果左侧触须接收到的气味强度比右侧强，那么天牛飞向左侧，否则就飞向右侧.根据这一简单原理，天牛可以有效地搜寻到食物.

为了便于说明，天牛在时间t(t=0,1,2…)的质心位置用向量pt表示，位置p处的气味浓度用f(p)表示，f(p)称为适应度函数.适应度函数的最大值对应于气味的源点.观察天牛的行为发现，天牛用触须搜寻食物气味时，主要有2种行为方式，即搜索和探测.搜索行为即天牛用触须寻找气味时，它们会随机搜索未知的环境.在现实生活中，天牛存在于三维空间，笔者为了使BAS算法有效地应用于任何维度的函数，在该算法中设计了一个随机的天牛搜索方向，以模拟天牛的搜索行为：

其中ran(·)表示一个随机函数，h表示空间的维数.由于天牛在寻找气味时头部的方向是任意的，因此天牛从右触须到左触须的方向也是任意的.为了简化天牛模型，在BAS算法中将天牛的质心坐标设置为p，左触须和右触须的坐标分别用pl和pr表示.这样，天牛的运动过程可以模拟为

(6)

其中d是天牛左右触须之间的长度.该长度应足够长，以避免在优化过程开始时落入局部最优值，其值会随时间逐渐减小.为了描述天牛的探测行为，结合天牛搜索行为模型(6)给出如下公式：

pt=pt-1+αtbsign(f(pr)-f(pl)).

(7)

其中：α是搜索的步长，初始步长可以尽可能大，最好等于自变量的最大长度；sign(·)表示符号函数；f(pr)，f(pl)分别表示位置pr，pl处的气味强度.利用搜索参数，即触须长度d和步长α，为算法设计提供更新规则，更新规则示例如下：

dt=ηdt-1+0.01，αt=ηαt-1，

其中η在0和1之间接近1，通常η设置为0.95.

3 BAS-MELM神经网络模型的建立

类ELM的泛化性能在很大程度上取决于其参数的选择.因此，笔者采用BAS算法来寻找MELM神经网络的最佳初始权值，并将其应用于MELM神经网络，以获得更优的MELM预测模型，从而构建最终的BAS-MELM训练模型.

建模步骤如下：

(ⅰ)构建BAS算法所需的方向向量.定义空间维度为w，将模型结构设置为U-V-1，U为输入层神经元数，V为隐层神经元数，输出层神经元数为1，于是搜索空间维数w=U×V+V×1+V+1.

(ⅱ)设置阶跃系数δ.阶跃因子δ用于控制天牛触须的区域搜索能力.初始步长应尽可能大，以覆盖当前搜索区域，而不会陷入局部极小值.本研究采用线性递减权值策略来确保搜索的精细化，即δt+1=δtη.

(ⅲ)选择均方根误差(Root Mean Squared Error，RMSE，用R表示)作为BAS算法的适应度评价函数，以促进空间区域的搜索，

(8)

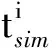
(ⅳ)BAS算法初始化.初始参数随机生成，作为BAS算法的初始解集，即天牛触须的初始位置，保存在bestP中.

(ⅴ)评估.根据(8)式计算初始位置的适应度值，并将其存储在bestQ中.

(ⅵ)天牛触须位置更新.根据(6)式更新天牛左右触须在空间中的位置坐标.

(ⅶ)适应度函数更新.根据BAS算法中天牛触须两侧的位置，求出该位置的适应度函数值f(pr)和f(pl).比较强度，根据(7)式更新天牛的位置，调整神经网络的权值，然后计算当前位置的适应度函数.若此时的适应度函数值优于bestQ，则更新bestQ和bestP.

(ⅷ)迭代停止控制.确定是否达到迭代次数，若达到，则转至步骤(ⅸ)；否则，返回步骤(ⅵ)继续迭代.

(ⅸ)获得最佳权值.当算法停止迭代时，bestP中的解就是训练的最优解，即MELM神经网络的最优初始权值.

4 模式分类实验

4.1 MELM的模式分类实验

采用公开的标准数据集Zoo评估MELM的性能.该数据集提供了100组数据，属性和类的个数分别为16和7.训练神经网络时，随机抽取50组数据，其余数据用于测试神经网络，实验结果如图2和图3所示.

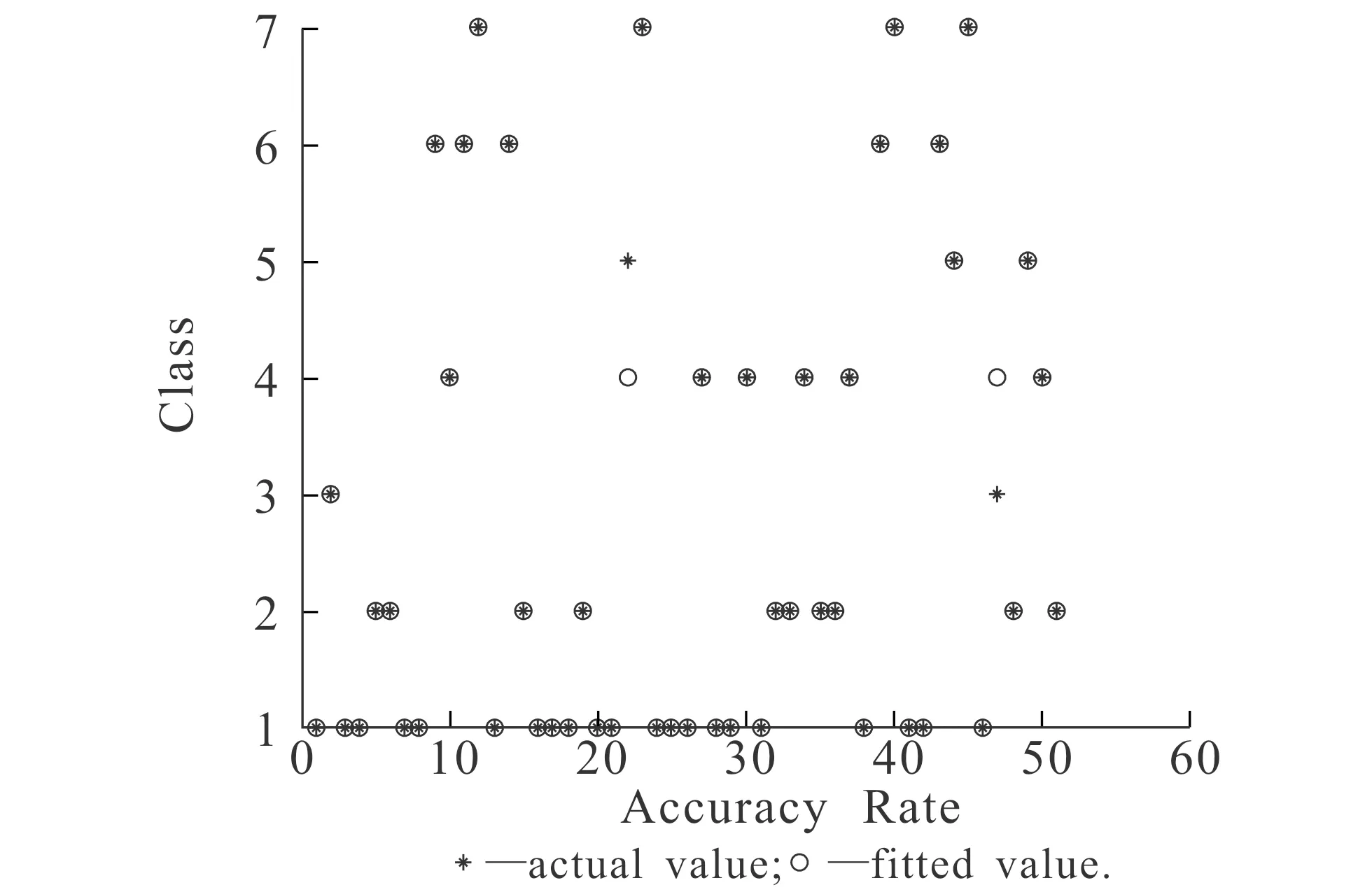
图2 Zoo数据集的训练结果

图3 Zoo数据集的测试结果

由图2和图3可见，MELM可以在训练和测试中很好地执行分类任务，测试和训练的最佳分类准确率分别为92.15%和88%.此外，通过实验发现，当隐含层神经元数量较小时，MELM的泛化性能就已达到稳定.具体来说，当隐层神经元数为2个左右时，分类准确度就达到最优并保持稳定.

笔者对比了MELM与其他神经网络(包括SOCPNN-W，MOCPNN-W，MLP-ELM，MLP-LM，RBFNN和SVM)[17]在达到最优分类时的隐层神经元数量，结果见表1.

表1 隐层神经元数量

从表1可知，与其他几种神经网络相比，在达到最优分类时，MELM所需的隐含层神经元数量最少，即MELM的结构最简单.这说明MELM的计算复杂度低于其他神经网络.MELM的隐层神经元数量将直接应用于后续BAS-MELM的模式分类实验中.

4.2 BAS-MELM的模式分类实验

采用UCI机器学习库中的典型现实世界分类数据集对MELM的性能进行评估，其特征见表2.在实验期间随机选择50%的数据集进行训练，其余的数据集用于测试.为了简单而又不失一般性，将隐层神经元的偏差B设置为0.此外，选用arctan函数作为神经网络的激活函数.

表2 实验数据特征

利用表2中的6组数据来训练和测试BAS-MELM神经网络的模式分类，并比较BAS-MELM与其他神经网络(包括SOCPNN-W，MOCPNN-W，MLP-ELM，MLP-LM，RBFNN和SVM)[17]的性能.对所有算法进行100次试验以避免初始参数设置过程中随机性产生的影响，并采用平均排序方法[18](即数字越小，泛化性能越好)对7个神经网络的泛化性能进行综合排序，结果见表3.

表3 测试集的平均分类准确度比较

从表3可知：对大多数数据集的测试集进行分类时，BAS-MELM都达到最高或第二高的平均分类准确度，即使对于某类数据的分类准确度不是最优结果，BAS-MELM的分类结果与最优结果之间的差距也很小；BAS-MELM的平均排名为2.17(最小值)，这说明BAS-MELM在7个神经网络中所有数据集的模式分类中表现最好，验证了BAS-MELM在模式分类中的有效性和优越性.

5 结语

笔者设计了一种改进的ELM，即MELM，它可以有效地应用于模式分类中.MELM的参数确定过程中，输出权值随机给出，并通过伪逆方法获得输入权值.MELM完成了ELM神经网络的逆向推导.笔者结合MELM，采用BAS仿生算法进一步优化了神经网络权值的选择.实验结果表明，与其他神经网络相比，BAS-MELM在进行模式分类时可达到更高的分类准确度，且隐层神经元数量最少.基于真实分类数据集的大量实验结果表明，与其他神经网络相比，BAS-MELM表现出其神经网络结构的简单性和有效性，以及在模式分类实验中具有良好的泛化性能.