不同空间方位异常体的直流电阻率法分析

张淼淼， 石显新

(1.煤炭科学研究总院， 北京 100013； 2.中国煤炭科工集团西安研究院有限公司， 西安 710077)

直流电阻率法是以岩层中岩石和矿石的电性差异为物质基础，由电极向地下供入电流，通过观测与研究人工建立的地中电流场的分布规律来进行地质勘探的一种电法勘探方法[1]。直流电阻率勘探无论是在金属、非金属矿产普查和地质构造研究方面，还是在水文地质调查、工程地质调查等方面，均发挥着重要的作用[2]。刘伟等[3]对低阻富水构造的多极距联合剖面曲线进行了二维正演模拟，对模型在二维中的倾斜状态进行了阐述。王志鹏等[4]利用高密度电法对断层进行探测，该方法对断层识别具有一定的有效性和准确性，但是对逆断层的探测效果明显好于正断层。孟麟等[5]采用井地电阻率法对起伏地形下陷落柱模型进行正演模拟，结果表明地形会改变陷落柱异常响应的形态和位置。通过上述研究可以发现，对于电阻率法探测断层，主要是基于在二维空间下的单一方位变化进行研究，而在其他地质异常体的研究中也主要是对地形变化对探测结果的影响。所以在三维空间下异常体不同方位对探测结果的影响需要进一步研究。

在运用直流电阻率勘探中，准确确定异常体实际位置与校正其位置偏差都非常重要，为了提高勘探效果，就需要对地质异常体的影响因素进行研究，其中对地质异常体的产状变化也很有必要，对于二维空间下异常体的空间变化只是单一方向的变化，而在实际探测中是具有不同空间方位的变化的。因此，现采用COMSOL有限元软件进行三维空间下不同方位的异常体进行直流电阻率研究，首先对点电源进行直流电法正演模拟误差验证，然后用板状体模拟断层，采用单极-偶极与偶极-偶极装置研究低阻板状体在空间方位上变化的异常响应特征，最后结合工程实例进一步分析验证，以期为直流电阻率法后期处理中准确识别断层等提供理论依据。

1 稳定电流场的基本理论

在稳定电流场的任意点上，电流密度矢量j与电场强度矢量E，则介质电阻率ρ与电流密度，电位U和电场强度之间有着如下关系[2]：

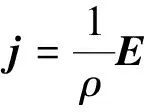
(1)

(2)

(3)

将式(1)和式(2)代入式(3)，则可以得

(4)

在无源均匀介质空间中，ρ为常数，则式(4)为

(5)

式(5)即拉普拉斯方程，它表示稳定电流场中不包含电流源在内的空间任何一点的电位只是空间位置的函数，在直角坐标系(x，y，z)中拉普拉斯方程表达式为

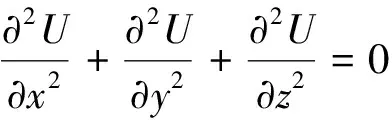
(6)

在球(r，θ，φ)坐标系中，有

(7)

在有源的均匀介质空间中，ρ为常数，有一点电源A(x0，y0，z0)，其电流强度为I，通过引入狄拉克函数δ(A)，得到满足电位与电流之间关系的微分方程，即泊松方程形式：

(8)

式(8)中：δ(A)是以点A(x0，y0，z0)为中心的狄拉克函数。

求出满足给定边界条件的泊松方程的解，即稳定电流场的边值问题，如图1所示，在求解电场问题时，边值问题有三种[6-8]。

在地面边界Γs上，电位的法向导数为

(9)

在无穷远边界Γ∞上，电位是点源电位：

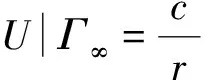
(10)

式(10)中：c为常数；r为点源到边界距离。对式(10)求偏导，消去常数c，得

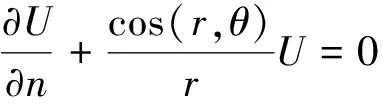
(11)

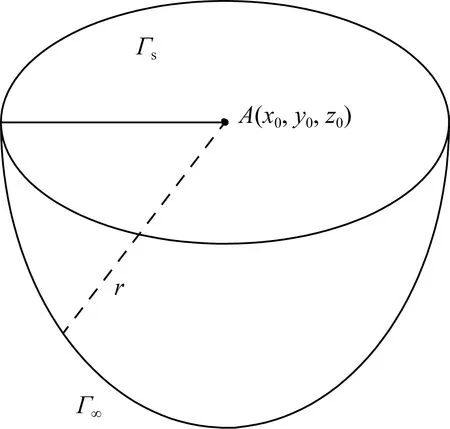
Γs为地面边界；Γ∞为无穷远边界；r为任意点A到无穷远边界Γ∞ 的距离图1 点电源边界示意图Fig.1 Sketch of point electric source boundary

2 误差分析

COMSOL软件是一款以有限元法为基础，通过求解偏微分方程的多物理场仿真软件，用来分析电磁学、结构力学、声学、流体流动和化工等众多领域的实际工程问题，COMSOL核心产品可以轻松实现建模流程的各个环节，为科研人员从常规有限元编程中解脱出来，COMSOL还拥有强大的求解器，可自动检测要求解的物理场，以及问题大小，并针对具体问题选择求解器，可以直接或迭代求解。在COMSOL中，用户可以自由控制模型的各个方面，其主要功能提供了基本的几何建模工具，也可以从AutoCAD制图软件导入模型。此外，还可以直接在图形用户界面使用方程式和表达式中输入用户自定义参数来进行仿真。COMSOL软件是基于有限元分析来模拟的，所以主要的分析过程与有限元大致相同，主要有三个步骤：前处理过程、求解过程和后处理过程。COMSOL分析的流程图如图2所示。

COMSOL的前处理阶段主要是建立几何模型、给定材料性质、设置边界条件、网格剖分。在COMSOL模拟仿真中，其模型建立的好坏将直接影响收敛的速度以及精度，所以在建立几何模型时，应该对实际模型进行简化处理，这样会减少求解的时间。在设置边界条件中，在距离点电源无穷远处可以假设电位为零，这样就可以满足第一类边界条件。但由于在COMSOL中建立太远边界，将会使得计算范围增大，从而导致计算时间太长，所以通过在模型周围建立无限元域即可防止模型过大。在地表边界处，空气的电阻率无限大而导致电流不能穿过，所以在模型中设置地表面电流密度的法向分量为零，满足第二类边界条件[9]。在COMSOL软件中无需设置内部连续条件，软件自动满足。

在有限元建模中网格的选择将会决定模拟的精度，在COMSOL中通过自适应网格优化解决这个问题，它首先在初始网格上求解，然后通过迭代将元素插入估计误差高的区域，然后重新求解模型，这样可以最大限度地减少模型中的总体误差。在COMSOL 软件中，可以根据需要来创建自由网格、扫掠网格和映射网格等，利用网格剖分工具，可以生成三角形、四边形、四面体和六面体等网格单元，而四面体网格的适应性较强，且容易实现局部网格加密，所以一般采用四面体网格剖分[10]。COMSOL有限元软件中的全局自适应网格细化方法通过使用误差估计，确定建模域中局部误差最大的点，在兼顾整个模型的局部误差的同时，同时在局部误差更显著的区域使用较小的单元。这种方法的好处在于，所有的网格细化工作均自动完成；其缺点是无法对网格进行控制。

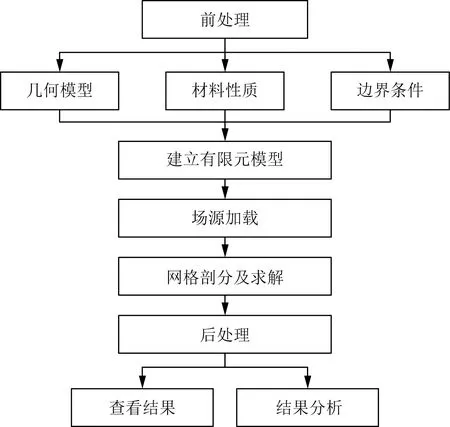
图2 COMSOL分析流程图Fig.2 Chart of COMSOL analysis

首先为了验证 COMSOL 软件对于地电模型正演的可靠性，通过建立三维均匀半空间的简单地电模型对其进行数值模拟。建立一个半径为10 m的半球体模型模拟均匀半空间，设置均匀半空间的背景电阻率为ρ=100 Ω·m，供电电极坐标(0，0，0)处，电流强度I=1 A，求取数值解并将与理论解进行对比。在三维均匀半空间中，点电源电位U解析公式为

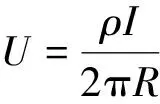
(12)

式(12)中：ρ为背景电阻率；R为观测距离。

表1给出了解析解和数值解的对比，从表1可知，在距离点源1 m处，相对误差为6.293 1%；在距离点源5 m处，相对误差为0.404 7%；而在距离点源10～50 m处，相对误差都小于0.100 0%。可以看出，在距离点电源较近的范围(小于3 m)，误差相对较大，越远离点电源，其误差越小。所以，可以看出COMSOL 软件对于直流电法三维地电模型的数值模拟结果是可靠的。

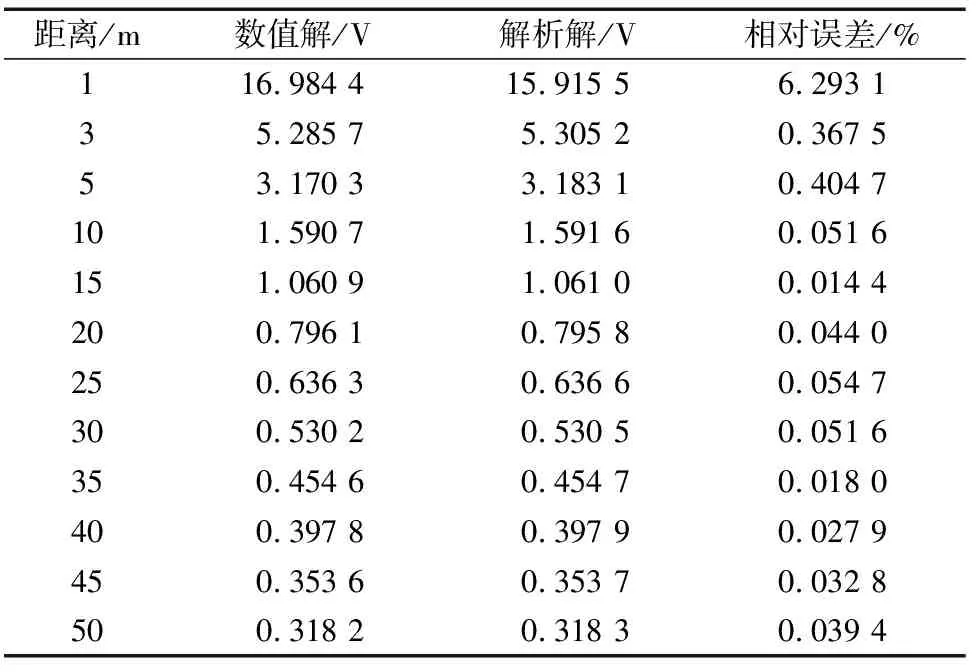
表1 三维点电源模型电位误差对比Table 1 Comparison of potential errors in three-dimensional point power supply models

3 低阻板状体直流电阻率模拟

3.1 板状体不同旋转方向数值模拟

3.1.1 模型1

设水平均匀大地电阻率背景值ρ1=100 Ω·m，在水平地面下方有一电阻率为ρ2=10 Ω·m的板状低阻异常体，模拟含水构造异常体，截面积10 m×10 m，厚度2 m，以板状异常体中心为圆心，沿Y轴顺时针旋转，旋转角度为0°、30°、60°、90°。根据模型采用单极-偶极与偶极-偶极装置进行观测计算。首先建立的模型一，原点位于地面正中心。其次先采用单极-偶极装置在地面A点(-70，0，0)供电，电流强度为1 A，M、N为测量电极，极距为5 m；然后采用偶极-偶极装置，A(-70，0，0)和B(-65，0，0)两点供电，电流强度分别为1 A和-1 A，极距5 m，两种方式测线距离为-60～60 m与-55～60 m。模型如图3所示。

图4给出了当埋深h=10 m时采用单极-偶极沿Y轴旋转的正演结果视电阻率曲线。从图4中的4条曲线可以看出，除曲线前端位置出现不同程度的波动以外，整体呈现出不对称形态。当长方体未进行旋转时即Y轴旋转0°曲线中可以看出，在极值异常两侧呈现左高右低的双峰形态，极值异常最小；随着顺时针旋转角度的增大，在旋转30°、60°、90°时极值异常两侧都呈现出左低右高的双峰形态，极值异常逐渐增大。正演结果显示，当板状异常体沿Y轴顺时针旋转时，双峰的高低与旋转方向呈现对应关系；且极值异常大小随着旋转角度的增大，异常幅值也在增大。

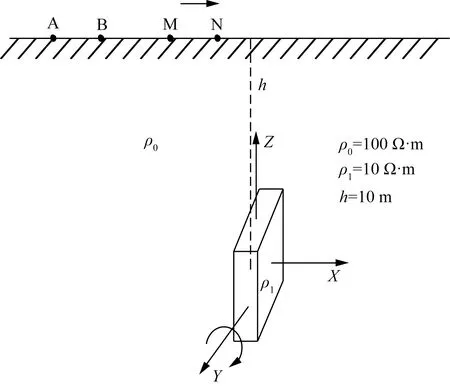
图3 模型1示意图Fig.3 Schematic diagram of model 1

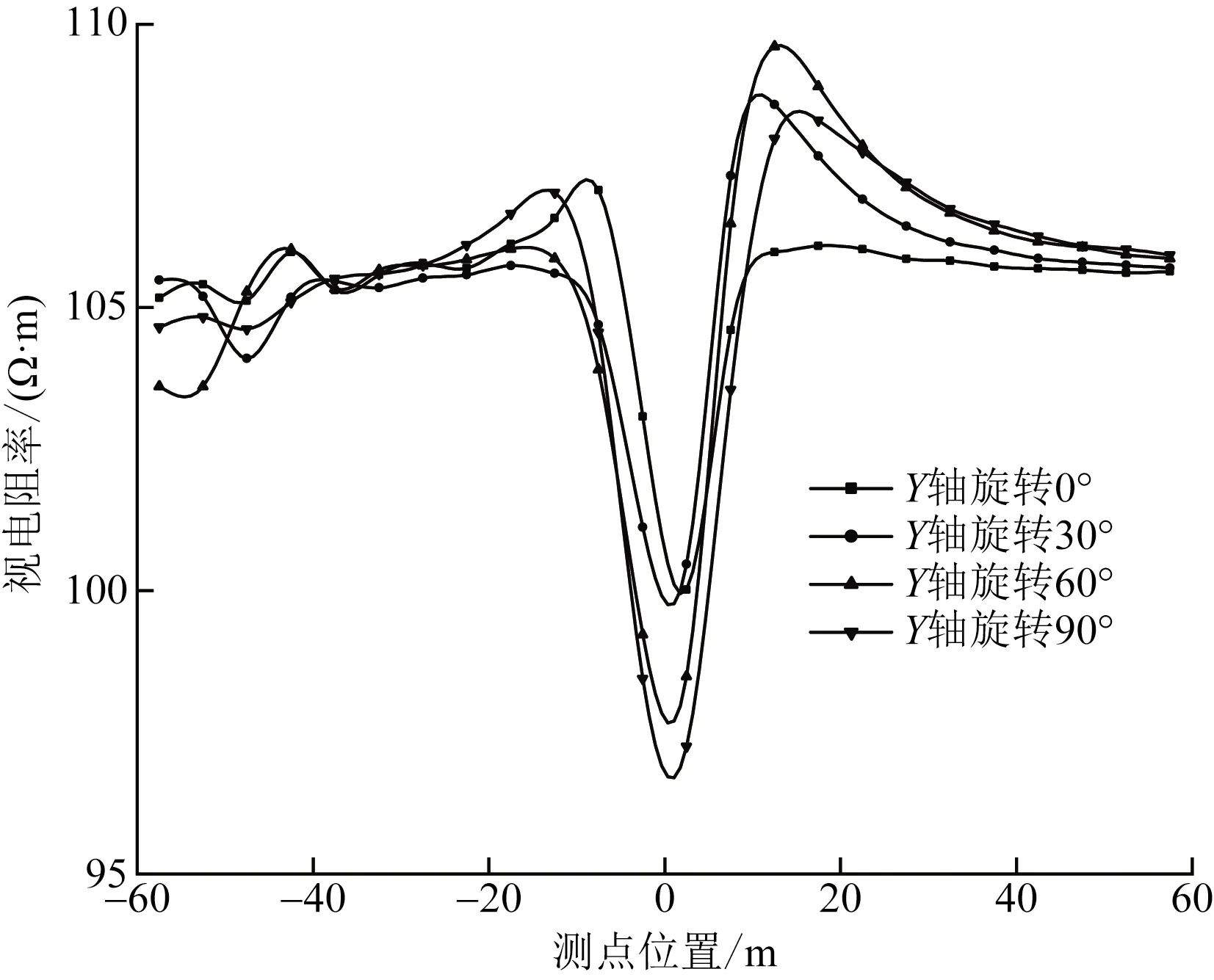
图4 模型1单极-偶极装置视电阻率曲线Fig.4 Apparent resistivity curve of pole-dipole device in model 1

图5给出了当埋深h=10 m时采用偶极-偶极装置沿Z轴旋转的正演结果视电阻率曲线。从图5中的4条曲线可以看出，除绕Z轴旋转30°曲线前端位置出现波动以外，其余3条曲线较光滑，而整体呈现出不对称曲线形态。而正演结果与单极-偶极模拟结果很相似，当板状异常体沿Z轴顺时针旋转时，双峰的高低与旋转方向呈现对应关系；极值异常大小随着旋转角度的增大，异常幅值也随之增大。

3.1.2 模型2

以板状异常体中心为圆心，沿Z轴顺时针旋转，旋转角度为0°、30°、60°、90°，其余设置与模型1一致。根据模型采用单极-偶极与偶极-偶极装置进行观测计算，模型2如图6所示。

图7给出了当埋深h=10 m时采用单极-偶极沿Y轴旋转的正演结果视电阻率曲线。从图7中的4条曲线可以看出，4条曲线前端位置都出现了一定波动，整体呈现出平滑的不对称曲线。当长方体沿Z轴旋转0°曲线中可以看出，在极值异常两侧呈现左高右低的双峰形态；随着顺时针旋转角度的增大，在旋转30°、60°、90°时极值异常两侧呈现出左低右高的双峰形态，极值逐渐减小。正演结果显示，当板状异常体沿Y轴顺时针旋转时，双峰的高低与旋转方向呈现对应关系，随着顺时针旋转角度增大，极值左边的单峰逐渐减小；且极值异常大小随着旋转角度的增大，异常幅值也在增大。

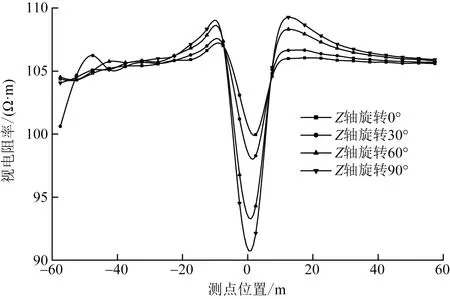
图5 模型1偶极-偶极装置视电阻率曲线Fig.5 Apparent resistivity curve of dipole-dipole device in model 1

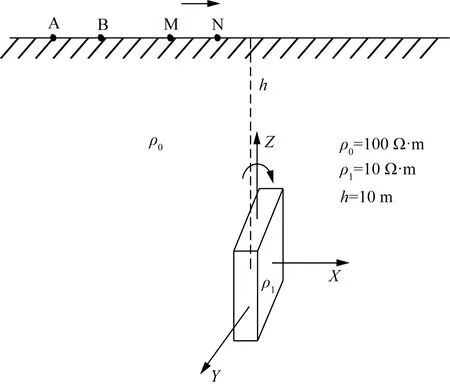
图6 模型2示意图Fig.6 Schematic diagram of model 2

图8给出了当埋深h=10 m时采用偶极-偶极装置沿Z轴旋转的正演结果视电阻率曲线。从图8中的4条曲线可以看出，有3条曲线前端位置都出现不同程度的波动，而整体呈现出不对称曲线形态。当板状异常体沿Z轴顺时针旋转时，双峰的高低与旋转方向呈现对应关系，随着顺时针旋转角度增大，极值左边的单峰逐渐减小；且极值异常大小随着旋转角度的增大，异常幅值也在增大。

通过低阻板状体在沿Y轴与Z轴旋转的模拟结果对比可以发现，两种模型双峰的高低与旋转方向都呈现相对应关系，但是在沿Z轴旋转时，需旋转角度较大(>60°)才有明显变化；两种旋转都随着旋转角度的增大，异常幅值也在增大。

图7 模型2单极-偶极装置视电阻率曲线Fig.7 Apparent resistivity curve of pole-dipole device in model 2

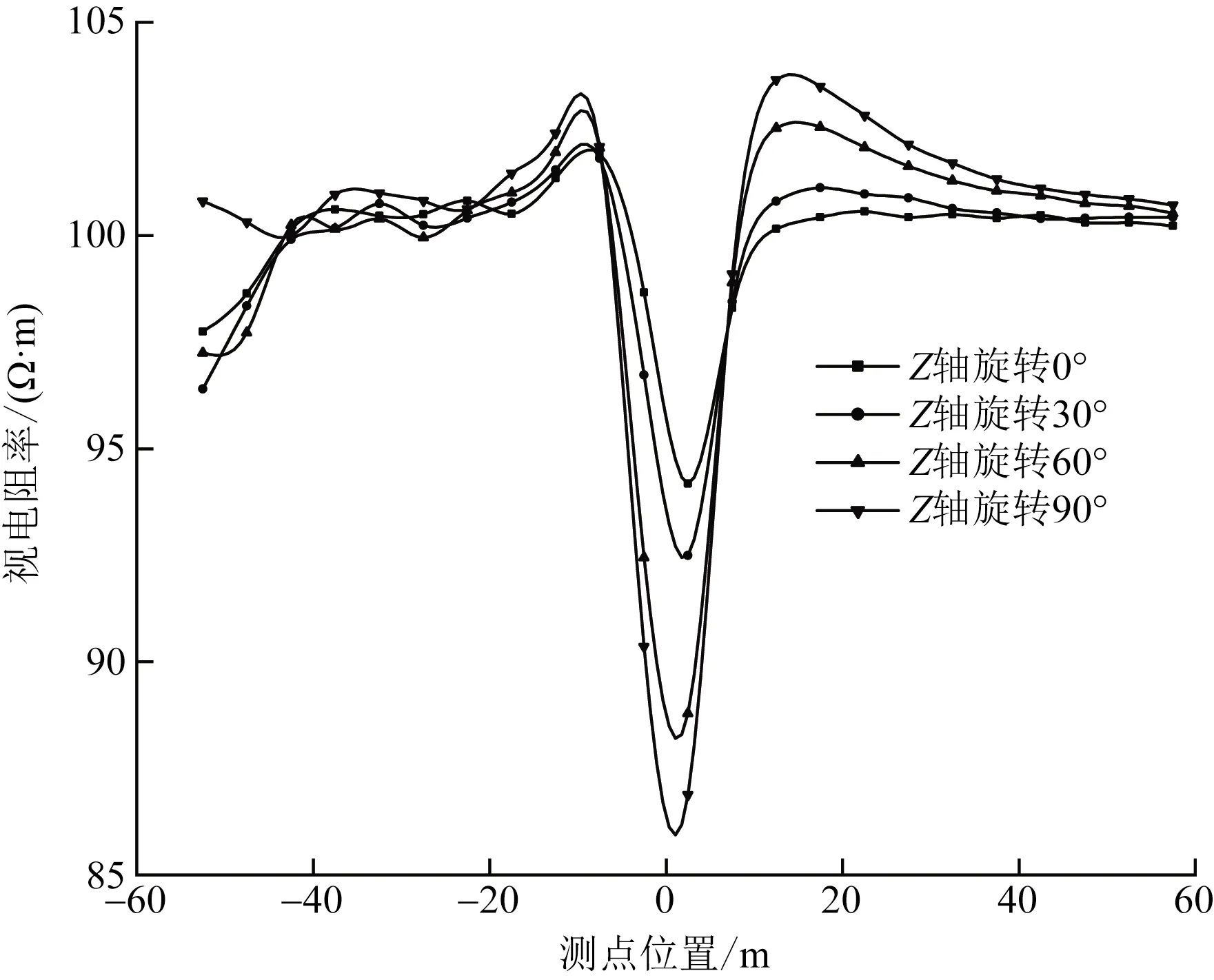
图8 模型2偶极-偶极装置视电阻率曲线Fig.8 Apparent resistivity curve of dipole-dipole device in model 2

3.2 不同旋转变化横向比较分析

上述分析主要是在每个角度的异常幅值以及形态变化上进行对比分析，但在横向上差异并不明显。因此，将视电阻率曲线图转换成视电阻率断面图，进一步分析异常体角度变化在横向上的差异。以单极-偶极装置视电阻率断面为例，如图9所示。

由图9(a)可知，当异常体绕Y轴旋转为0°时，可以准确反映异常体位置，但异常范围较小；随着旋转角度增加，低阻异常所在位置相对于真实位置有所提前，且异常范围开始变大。由图9(b)可知，当异常体绕Z轴旋转，异常范围变化很小，但随着旋转角度的增加，异常体的位置有所提前。

因此，在用直流电阻率勘探中，应综合考虑地质构造的产状，从而对异常体进行校正、归位。

4 工程实例

为了进一步说明断层对直流电阻率法结果的影响，选取野外探测实例进行说明。为保证广西南宁至玉林城际铁路某段建设安全，在该段内进行断层等地质灾害的勘测。

该段地表植被发育，地表为第四系覆盖，主要岩性有白垩系、寒武系泥岩、砂岩，物性参数如表2所示。由表2可知，第四系、白垩系砂岩夹泥岩之间存在一定的电性差异，较完整岩体破碎、较破碎或含水岩体之间在电阻率值和等值线形态有明显的区别，因此该工区具备开展直流电阻率法的地球物理勘探条件。

表2 物性参数统计表Table 2 Statistical table of physical parameters

在该区段布置一条#1高密度测线，选用温纳装置进行观测，电极间距5 m，最大隔离系数为31，通过逐次扩大电极距a值，使探测深度逐渐加深，观测测点处垂直方向由浅到深的电阻率变化。资料处理采用瑞典高密度二维反演软件RES2DINV，最后将反演数据利用Surfer及 AutoCAD软件绘制成果图。

图9 单极-偶极视电阻率断面图Fig.9 Profile of apparent resistivity of pole-dipole device

图10 视电阻率断面图及地质断面图Fig.10 Apparent resistivity section and geological section

测线视电阻率断面图和地质断面图如图10所示，由浅及深电阻率可以分3层，浅地表电阻率较为不均匀，推测其主要为第四系、覆盖层，电阻率较低，为10～30 Ω·m；测点距离0～400 m：中间层为白垩系砂岩夹泥岩，较破碎，电阻率ρ=10～20 Ω·m，下部为白垩系砂岩夹泥岩，较完整，电阻率ρ=20～60 Ω·m；测点距离400～800 m：中间层为寒武系砂岩夹泥岩，较破碎，电阻率ρ=10～100 Ω·m，下部为寒武系砂岩夹泥岩，较完整，电阻率ρ=100～500 Ω·m；测点距离300～400 m，电阻率等值线变陡呈低阻纵向延伸，通过后期钻探资料得知，由断裂引起，断层破碎带，与基岩倾角约60°，电阻率ρ=10～50 Ω·m。

从图10(a)与图10(b)对比中可知，在地质断面图中断层的真实位置大概在测线300～400 m，而图10(a)中通过高密度电法所测得的断层范围显示在测线400～550 m。因此，在进行直流电阻率法测量断层等异常时，倾角变化会导致其真实位置发生偏移，且异常范围也会增加，在后期应进行校正处理才能精确定位。

5 结论

(1)采用COMSOL软件对三维半空间模型正演模拟，通过验证数值解与解析解的误差，可以知道利用COMSOL软件进行三维半空间模型正演计算是可行的。

(2)在模型模拟中，采用单级-偶极装置和偶极-偶极装置来模拟低阻板状体绕Y轴与Z轴的变化，绕Y轴旋转其极值两侧双峰的高低与旋转方向有很大关系，但是在沿Z轴旋转时，需旋转角度较大(>60°)才有明显变化；两种旋转都随着旋转角度的增大，异常幅值也在增大。

(3)两种旋转方式在横向上的变化，随着绕Y轴旋转角度增加，低阻异常所在位置相对于真实位置有所提前，且异常范围增大；绕Z轴旋转，异常范围变化较小，位置有所提前。

(4)实际数据得到的反演结果与数值模拟的结论相吻合，当有倾角断层时，会导致直流电阻率法结果出现断层真实位置偏移，异常范围增加，所以应对后期结果进行校正才能准确定位。