双能图像融合算法研究
洪晓洁,金 晓,张成鑫,3
(1.中国工程物理研究院研究生院,四川绵阳 621999;2.中国工程物理研究院应用电子学研究所,四川绵阳 621900;3.中国工程物理研究院应用电子学研究所加速器及应用技术中心,四川绵阳 621900)
在工业X 射线检测中,特别对于复杂工件来说,单能的DR 成像(数字X 射线成像)会出现图像质量下降、受材料和厚度影响大甚至细节丢失等问题,因此解决这类问题显得尤为重要。文中采用双能和小波技术相结合的图像融合算法,进一步增强图像细节,达到较理想的融合效果。图像融合是指对多个通道采集到的数据,提取其最有利的数据,融合成一幅高质量图像的过程。高效的图像融合方法可以综合地处理多通道信息,提高信息的利用率和准确性,提高原始图像的空间分辨率和光谱分辨率。所以图像融合在很多领域都有广泛的应用,比如计算机视觉、医学、遥感技术和军事等领域[1]。
图像融合由低层级到高层级依次是数据级融合、特征级融合以及决策级融合[2],其中数据级融合也称作像素级融合,它能够直接对采集的数据进行处理,是高层次图像融合的基础,它的优点在于尽可能地保护原始数据,最大化地提供细节信息,精度较高。像素级融合中有空间域和变换域算法,灰度加权平均法[3]、逻辑滤波法和对比调制法属于空间域算法[4]。金字塔分解融合法和小波变换法属于变换域算法,其中小波变换法是比较主流的算法。特征级融合是把各个传感器里的特征信息提取出来,再进行进一步的分析和处理。决策级融合主要在于主观的要求,比如贝叶斯法、表决法和D-S 证据法等[5]。每种方法都有其的优缺点,目前来说,数据级(像素级)融合方法最为主流,也是文中所采用的。文中给出的双能图像融合方法主要步骤:首先对高能和低能的DR 图像进行小波分解,然后将提取的低频和高频分量进行融合,最后采用小波重构算法生成最终的融合图像。
1 小波变换分析
1.1 基本小波
小波是一种频率窗和时间窗都可以改变的时频分析方法[6],它的窗口面积不变,但是窗口的形状会随着频率的高低变化。小波变换在低频时,有较低的时间分辨率和较高的频率分辨率,在高频时,有较高的时间分辨率和较低的频率分辨率,对局部特征的表征能力比较强[7]。
设ψ(x)∈L2(R),其傅里叶变换为Fψ(w),若Fψ(w)满足条件:

则称ψ(t)为一个基本小波(母小波),将ψ(t)进行伸缩和平移后得到:
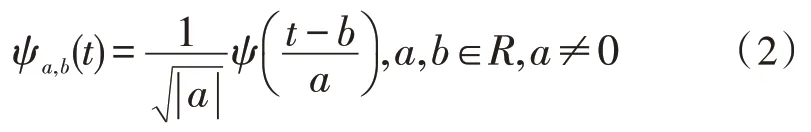
1.2 小波的分解
DWT 离散小波变换技术是按照幂级数对尺度函数进行离散化的处理,如下:

小波分解的实质就是利用对信号进行离散小波变换,当信号传输到滤波器时,高通滤波器分解为高频分量,也称为细节分量,低通滤波器分解为低频分量,也称近似分量,该过程对应的算法称为Mallat 算法。Mallat 算法的基本思想是设Hj f为能量有限信号在分辨率2j下的近似,则Hj f可进一步分解为在分辨率2j-1与2j之间的Dj-1f之和,其分解过程如图1 所示。

图1 高频和低频分解过程
1.3 信号分解重构
设:

信号分解和重构就转化成寻找和与之间的关系,可以通过推导得到分解系数的表达式:

因此重构系数的表达式为:
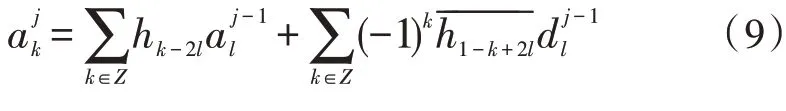
2 图像融合算法
图像融合是把融合的方法运用到低频系数和高频系数当中。图像融合的目的是增强图像的利用率和信息的精度,把两幅或者多幅图像融合在一起[8],进行综合处理,得到一幅信息全面、精度较高、满足需求的图像。
2.1 低频融合规则
因为小波低频融合[9]主要反映图像周围的整体框架,所以能够很好地保留图像的轮廓细节信息,解决一些单能X 射线图像中的细节不突出问题,达到增强图像细节的目的[10]。
G(X,p)表示图像X在以p点为中心的Q区域的区域方差显著性,如下:
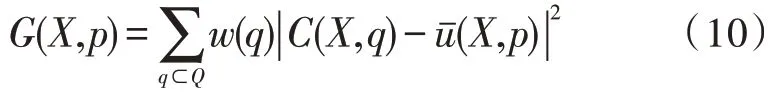
其中,w(q)表示权值。图像A和B的区域方差显著性表示为G(A,p)和G(B,p)。用M2(p)定义图像A和B在p点的区域方差匹配度:
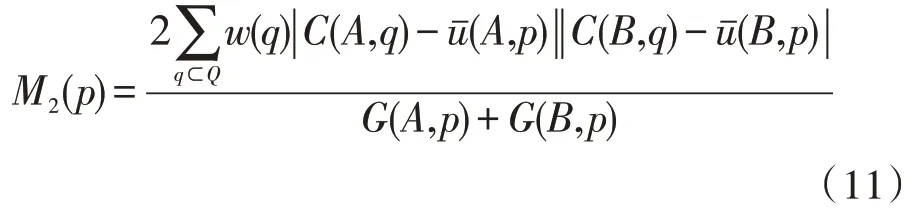
M2(p)的取值范围为(0,1),相关程度与取值大小有关,取值越大,相关程度越大。设N2为匹配度阈值,取值范围为(0.5~1)。
当M2(p) 当M2(p)≥N2时,采用的是平均融合,如式(13)所示: 这种低频融合方法能够最大程度地保留框架细节,增强图像的成像质量,达到预期目标。 融合规则在图像融合中起到很重要的作用,高频分量反映的是图像的细节信息,最大化地保留图像丰富的细节信息尤为重要[11],所以这里采用Sobel边缘检测算子来检测细节信息,再根据检测到的细节信息提取高频分量。一个Sobel 算子[12]检测水平边缘,一个Sobel 算子检测垂直边缘,进而计算图像的灰度近似值。其卷积因子如下: Hx、Hy分别是水平方向和垂直方向的矩阵,和图像作卷积就可以得到水平方向和垂直方向的亮度差分近似值。用I0代替原始图像,可以得出: 设f(a,b)为图像在x=a,y=b的灰度值,计算公式如下: 将得到的水平灰度值和垂直灰度值进行结合,算出该点灰度值的大小: 如果梯度H大于某一阈值,就认为它是边缘点。在高频融合部分采用的是取最大梯度值再加权的融合规则:在高频系数矩阵外添上0,方便把同一级同一方向的矩阵进行分块。把它们分成N×N的矩阵块,求出每个矩阵块的梯度之和,把这个和作为矩阵块中心点的梯度值。用这些中心点的梯度值构成新的梯度矩阵,再比较同一级同一方向的梯度值,取梯度值最大的高频系数,构成高频融合子带。 将上述方法应用到工件的检测中,该文采用某复杂金属构件作为模体(型号为AIS19Cu3),进行实验和分析。 在该实验中,采用高能和低能对模体进行DR 成像,射线源使用的是COMET XP450 MXR451HP/11,探测器使用的是XRD 1611 AP14,在低能DR 成像中,管电压为80 kV,管电流为4 mA,积分时间为1 000 ms;高能DR 成像中,管电压为320 kV,管电流为1 mA,积分时间为500 ms。图2 为实验装置,将模体和线对卡固定在转台上,可以采集到原始的高能和低能DR 图像,如图3和图4 所示。 图2 实验平台装置图 图3 高能DR成像 图4 低能DR成像 利用文中的融合方法进行融合,融合后得到的图像如图5 所示。 图5 融合后图像 可以采用信息熵[13]、空间频率和方差[14]对图像进行参数比较[15-20],也是通过定量来评价该文方法的有效性。各参数的比较如表1 所示。 从表1 可以看出,利用该文方法融合后的图像的信息熵比融合前的信息熵大,融合后的空间频率和方差都比融合前的图像要大,这说明了这种融合方法使得融合后的图像比融合前的图像有更多细节信息,具有一定的应用价值。 表1 融合图像性能参数比较 文中给出了结合双能和小波技术的图像融合算法。先进行小波分解,用基于邻域像素的关联性和区域方差提取低频分量。再用Sobel 算子检测局部细节信息,梯度最大值作为算子检测的图像边缘输出,提取高频分量。最后用小波重构算法对处理后的小波系数进行反变换重建,即可得到融合图像。在提取高频信息时,即提取局部信息时,过往通常采用Krisch 边缘检测算子从8 个方向检测局部细节信息。该文创新性地采用Sobel 算子检测水平边缘和垂直边缘,再将图像作卷积就可以得到水平方向和垂直方向的亮度差分近似值。这种方法能有效提取图像边缘处细节。低频信息和高频信息的双能融合可以对低能和高能进行信息互补,较好地保护了图像的细节,增强了图像的成像质量,提高了工业测量的准确性,在工程上具有广泛的应用前景。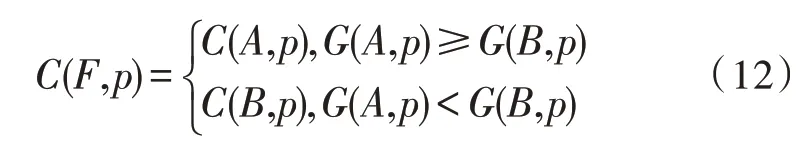
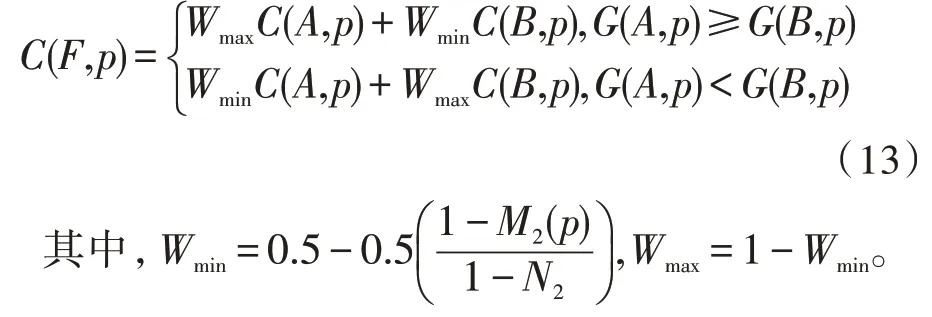
2.2 高频融合规则




3 实验结果及分析





4 结束语

