基于DPCA 残差互异度的故障检测与诊断方法

张 成 戴絮年 李 元

在现代工艺中,企业对系统更安全更可靠的需要推动了过程故障检测技术的快速发展.该类技术通过及时检测过程扰动、设备故障等特殊事件,不仅在保证工艺和人员安全方面起到了重要作用,而且提高了工艺效率和产品质量.随着分布式控制系统(Distributed control systems,DCS)对大量变量的自动测量和存储,多元统计过程监控(Multivariate statistical process monitoring,MSPM)方法被成功地应用于各种工业过程的在线监控领域[1−3].

针对相关过程变量引起的共线性问题,主元分析(Principal component analysis,PCA)[4−5]和偏最小二乘(Partial least squares,PLS)[6−7]等方法相继被提出并在化工过程检测领域得到了广泛的应用.PCA 在过程检测时通常将原始空间分为主元子空间(Principal component subspace,PCS)和残差子空间(Residual subspace,RS),然后分别使用Hotelling＇sT2和平方预测误差(Square prediction error,SPE) 作为统计量来监控样本状态[8].其中,T2是归一化主元得分平方和,即对PCA 模型内变化的度量,而SPE是平方误差之和,即对PCA模型未捕获变化量的度量.为了检测非线性过程,基于核理论的主元分析方法被提出,即核主元分析(Kernel PCA,KPCA)[9].KPCA 的基本思想是首先通过非线性映射将低维样本数据映射到高维特征空间,然后在特征空间中执行PCA 完成故障检测[10−11].值得注意的是,PCA 和KPCA 方法均应用T2和SPE两个统计量进行过程状态监控.T2和SPE能够较好完成过程监控的前提条件是变量服从多元高斯分布且样本间相互独立[12].事实上,众多生产过程,如石油化工、半导体蚀刻工艺等,变量间存在较强的非高斯特征且样本间存在自相关特征[13],这些显著特征制约了上述方法的故障检测性能.针对上述不足,Ku 等提出了动态主元分析(Dynamic PCA,DPCA)[14].DPCA 通过“时滞移位”方法将过程的静态信息和动态信息实现同步提取.在进行故障检测时,DPCA 同样采用T2和SPE统计量监控样本状态.SPE统计量主要衡量样本在空间上的变化信息,而没有考虑样本存在时间信息上的变化.因此当样本具有时刻相关性时,SPE统计量通常无法及时检测出故障.Kano 等定义了一个互异度指标来监测过程时间序列数据的分布[15].在故障检测时,互异度方法和DPCA 使用不同的统计量监控样本状态.互异度方法通过对具有不同特征的过程数据分布进行定量分析来检测典型连续过程中操作条件的变化.近年来,许多学者对互异度方法进行了深入研究并取得了丰硕的成果,如Wang 等提出了基于互异度方法的渐进式故障检测与诊断方法,Zhao等将互异度方法应用于批次过程故障检测中.一系列成功的理论研究和应用表明,互异度方法能够快速、有效地检测过程变量间相关性的变化[16−17].

DPCA 方法能够提取过程的动态变化信息,其在化工过程故障检测方面的有效性已经得到了验证[18−20].然而,文献[21]指出,由DPCA 获得的主元和残差中仍然保留了较强的自相关性.这种特征降低了T2和SPE控制图的故障检测性能.针对动态主元分析方法中残差自相关性降低过程故障检测率问题,本文提出基于DPCA 残差互异度的故障检测与诊断方法.首先,通过DPCA 方法将输入数据空间划分成主元子空间和残差子空间.接下来,对于残差得分应用滑动窗口技术并结合互异度指标完成对样本状态的监控.该方法能够降低过程动态特征对故障检测的影响,通过仿真实验进一步证明了本文方法的有效性.

1 动态主元分析和互异度指标

1.1 动态主元分析

假设X=[x(1)x(2)··· x(m)] 为包含m个样本的数据集,其中x(i)∈Rn(i=1,2,···,m) .若过程的时滞参数lag=k,则可通过式(1)生成包含过程静态特征和动态特征的增广矩阵,

接下来,对Y通过式(2)进行标准化处理,

其中,m和 Σ 分别为Y的均值向量和标准差对角阵,ξ为元素全为1 的列向量.标准化后的增广矩阵的协方差矩阵可由式(3)计算得到,

根据式(4)可计算C的特征值λ和特征向量p,

记C按降序排列的特征值与相应的特征向量依次为λ1,λ2,···,λn×(k+1)和p1,p2,···,pn×(k+1),依据累计方差贡献率(Cumulative percent variance,CPV)可将特征向量分为主元负载矩阵=[p1p2··· pr]和残差负载矩阵=[pr+1pr+2···pn×(k+1)],其中,r为被保留的主元数.于是,可通过式(5) 和(6) 计算样本的主元得分和残差得分,

1.2 互异度指标

记X=[X1,X2],于是X的协方差矩阵可表示为:

其中,N=N1+N2.将R通过式(11)进行特征分解:

其中,Ξ 为R的特征值构成的对角矩阵,P0为相应的特征向量矩阵.构造变换矩阵P1:

同时,P1与R满足:

将数据集Xi做如下变换:

则矩阵 Ψi的协方差矩阵可表示为:

通过式(10)、(12)和(15)可得:

由式(16)和(17)可得:

式(17)和(18)说明,S2与S1具有相同的特征向量,而其特征值满足如下关系:

2 基于DPCA 残差互异度的故障检测与诊断方法

在DPCA 方法中,通常采用SPE统计量对过程数据残差得分进行监控.该统计量可以进一步整理为如下形式:

可以看出,SPE统计量本质上在监控样本的残差得分到坐标原点的距离.为了保证SPE统计量的有效性,进一步要求过程数据残差得分应具有较低的自相关性.事实上,由DPCA 所捕获的残差得分通常存在较强的自相关性.接下来,通过一个简单的数值例子进行分析验证上述结论,主要模型如式(22)所示:

其中,u(i)=0.7u(i −1)+w(i −1),u(0)=0,w是均值为0、方差为1 的高斯白噪声.由式(22)生成1 000个样本,在时滞参数lag=1 的前提下应用DPCA方法对上述数据集X=[u z] 进行分析.记为X被标准化的增广矩阵,的协方差矩阵特征值如图1 所示.由图1可以看出,最后一个特征值较小且接近于0,这说明通过分析使得过程的动态特征被捕获.在本例中,由于3 个主元可以包含原始数据99.7%的变化信息,因此被保留的主元数设置为3.

图1 主元累计方差贡献率Fig.1 Cumulative percent variance of principal component

接下来,通过式(23)分析本例中残差得分的自相关性.

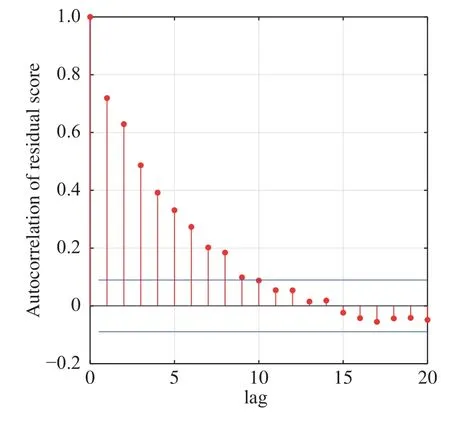
图2 DPCA 残差得分自相关性Fig.2 Autocorrelation of residual score in DPCA

本文结合DPCA 方法能够有效捕获过程动态特征和互异度指标能有效监控具有自相关性数据的优势,提出基于DPCA 残差互异度的故障检测与诊断方法(Fault detection and diagnosis based on residual dissimilarity in dynamic principal component analysis,DPCA-Diss).DPCA-Diss 故障诊断过程主要由以下三部分构成:离线建模、在线检测和故障诊断.

2.1 离线建模

值得注意的是,本文采用经验法确定统计量的控制限.经验法的一般性描述如下:99%置信上限确定为位于99%检验样本所在位置的统计值,即在该统计值以下可以找到99%的校验样本.经验法确定控制限的意义在于可以为不同方法提供公平的比较[22].

2.2 在线检测

2.3 故障诊断

当 Θ(k) 被识别为过程故障时,其相应的故障诊断方案如下.

注 1.DPCA-Diss 方法结合了DPCA 和互异度指标两种方法的优点,既可以获取过程数据的动态信息,又能消除数据的自相关性对故障检测的影响.但是DPCA-Diss 方法并不是两种方法的简单结合.DPCA 方法既可以对数据进行维数约减,又能获取数据的动态信息,但是DPCA 无法有效消除数据自相关性对过程状态监控的影响.互异度方法虽然可以解决数据自相关性的问题,但是当工业数据具有较多变量时,计算复杂度会增加.同时,基于互异度方法的故障检测策略无法直接通过控制图观测出故障产生原因.DPCA 和互异度两种方法可以优势互补,因此,本文结合两种算法的优势,提出了DCPA-Diss 方法,并且给出了基于贡献图的故障诊断策略,该策略解决了互异度方法无法通过控制图查找出故障原因的问题.

3 数值例子

在本节中文献[14]中的一个动态过程例子被用于测试本文方法的有效性.具体模型如式(25)和(26)所示:

其中,v=[v1v2]T是均值为[0 0]T,方差为[0.120.12]T的高斯白噪声;u是过程相关输入且满足:

其中,w=[w1w2]T是均值为[0 0]T,方差为[1 1]T的高斯噪声,u(0)=[0 0]T.依文献[22]所述,在本例中监控数据集由过程相关输入u和过程输出y构成.由以上模型随机生成两组各包含2 000 个样本的数据集用于确定DPCA-Diss 方法的控制限.为了验证DPCA-Diss 的有效性,由该模型生成包含2 000个样本的测试数据集F.在F中,从第1 001 s起w1的均值由0 变化为2 并持续到过程结束.

在本节中,传统的PCA 和DPCA 方法对本例也进行了测试.各种方法具体参数设置如下:1)在PCA 中,PCs=3;2)在DPCA 中,时滞参数lag=2,PCs=5;3)在DPCA-Diss 中,经交叉验证确定窗宽为100,滑动步长为1.各种方法的故障检测率(Fault detection rate,FDR)如表1 所示.

表1 各种方法故障检测率Table 1 Fault detection rates using different methods

图3 为PCA-SPE的故障检测结果,可以看出该方法并不能有效识别动态过程的异常变化,因此故障检测率仅为4.4%.DPCA 可以捕获过程的动态特征,因此DPCA-SPE的故障检测率相比PCASPE有所提高,但是仅达到了16.6%,如图4 所示.DPCA-SPE故障检测率仍然较低的主要原因是其残差中存在较强的自相关性,如图5 所示.DPCADiss 的故障检测结果如图6 所示,可以看出DPCA-

图3 PCA-SPE 故障检测结果Fig.3 Fault detection results using PCA-SPE

图4 DPCA-SPE 故障检测结果Fig.4 Fault detection results using DPCA-SPE

图5 DPCA 残差得分自相关性Fig.5 Autocorrelation of residual score in DPCA

图6 DPCA-Diss 故障检测结果Fig.6 Fault detection results using DPCA-Diss

Diss 方法在本例中具有最高的故障检测率,达到95.1%.因为Diss 可以有效提取数据在时间上的变化信息即自相关性.以上故障检测结果说明本文方法在降低残差得分自相关性影响的同时能够提高动态过程故障检测率.图7 给出DPCA-Diss 方法的故障诊断结果.可以看出,在第1 051 s～ 1 055 s时间内,变量u1的贡献显著大于其他变量的贡献,这一结果说明,过程的异常变化主要是由于变量u1发生变化引起的.事实上,由于u1是w=[w1w2]T的线性组合,当w=[w1w2]T中心发生漂移时必将引起u1的异常发生.由图8 可以看出,1 001 s 后数据的变量中心发生了明显的偏移,这与DPCA-Diss诊断结果一致.

图7 监控变量贡献图Fig.7 Contribution charts of the monitored variables

图8 输入变量uFig.8 Input variable u

4 Tennessee Eastman 过程

1993 年,Downs 和Vogel 设计了TE 过程仿真器,截止目前,该仿真器已经被广泛应用于过程监控领域并取得了许多先进的研究成果[23−24].TE 过程包含反应器、冷凝器、汽液分离器、循环压缩机和产品汽提器5 个基本操作单元,如图9 所示.由该过程采集的数据包含12 个操纵变量、22 个连续过程测量变量和19 个成分测量变量.本节采用已经被广泛使用的TE 数据集进行仿真测试,该数据集在TE 仿真器中通过3 分钟采样间隔并持续运行48小时获得[25].训练集中包含960 个正常状态下采集到的样本,同时,过程故障在8 小时后引入并持续到过程结束.如文献[26]所述,在本节中对上述数据集中的33 个变量进行监控.

图9 TE 过程Fig.9 Layout of TE process

在DPCA-Diss 方法中,采用包含480 个正常样本的校验集合进行过程故障检测控制限的确定.本例中lag=1,55 个主元被用于建立模型,同时,窗宽设置为60,滑动步长为1.为了对比分析,本节对PCA、KCPA、DPCA 和Diss 方法也进行了实验.表2 给出上述方法的故障检测率.综合对比上述方法对于TE 故障的检测效果,PCA 和KPCA方法的检测率相对较低,其原因是这两种方法均无法获取数据的动态信息.DPCA 相较于前两种方法检测率有所提高,主要原因是该方法可以有效捕获数据的动态信息.但对于部分故障DPCA 检测率仍旧较低,原因是这些故障具有较强的自相关性.在TE 原始数据集上使用Diss 方法进行故障检测时,其对于大部分故障检测率依然较低,其根本原因是TE 过程数据变量较多,数据自相关特征不显著.DPCA-Diss方法的总体检测效果最优,主要原因是该方法既可以提取数据的主要动态信息,又可以成功消除数据自相关性对故障检测的影响.

表2 各种方法故障检测率(%)Table 2 Fault detection rates using different methods(%)

接下来,通过两个具体的故障对DPCA-Diss方法进行分析.图10 和11 分别给出PCA,DPCA和DPCA-Diss 方法对故障5 和19 的检测结果.对于故障5 而言,由于DPCA 成功获取了过程数据的动态信息,因此本文方法与DPCA-SPE具有较高的故障检测率,均达到99%以上.而在故障19 的检测故障中,虽然DPCA 方法获得了过程数据动态信息,但是残差得分仍存在自相关性,而本文方法有效解决了该问题,因此本文方法故障检测率显著高于其他两种方法.

图10 故障5 检测结果Fig.10 Detection results of Fault5

为了进一步确定故障产生的原因,图12 和13分别给出了故障5 和故障10 的诊断结果.故障5是在仿真8 小时后由冷凝器冷却水入口温度发生阶跃变化引起.由于没有测量冷却水入口温度,所以操纵变量冷凝器冷却水流速 (x33) 是最相关的变量,如图14 所示.故障10 是由C 进料温度发生随机变化引起的,基于TE 过程的机理,这种变化必将引起汽提塔温度 (x18) 的异常变化,如图15 所示.故障5 和故障10 的诊断结果与实际一致,结果验证了本文诊断策略的有效性.

图11 故障19 检测结果Fig.11 Detection results of Fault19

图12 故障5 贡献图Fig.12 Contribution chart of Fault5

图13 故障10 贡献图Fig.13 Contribution chart of Fault10

图14 变量33Fig.14 Variable 33

图15 变量18Fig.15 Variable 18

5 结论

针对动态主元分析方法中残差自相关性降低过程故障检测率问题,提出了基于动态主元分析残差互异度的故障检测与诊断方法.本文方法通过滑动窗口技术与互异度指标相结合降低了过程动态特征和数据自相关性对故障检测的影响;同时,本文给出了基于贡献图的故障诊断策略,解决了无法通过控制图获取故障产生原因的问题.对比传统的故障方法,本文提出的方法具有更优异的故障检测性能.

本文采用的滑动窗口技术对发生于初始时刻的故障检测通常较为迟缓,因此接下来的研究方向为对初始时刻发生的故障进行及时有效地监控.