外电场下含有缔合缺陷的ZnO/β-Bi2O3界面电学性能*

李亚莎 刘世冲 刘清东 夏宇 胡豁然 李光竹

(三峡大学电气与新能源学院,宜昌 443002)

电力设备的安全运行很大程度上取决于避雷器的过电压保护水平,ZnO压敏电阻因具有优异的非线性伏安特性而广泛应用于电力系统避雷器的核心元件.为了从微观结构上了解ZnO压敏电阻的电学性能,本文采用基于密度泛函理论的第一性原理对含有锌填隙Zni与氧空位Vo缺陷的ZnO/β-Bi2O3界面进行分析计算,并研究其在不同外电场下的相关电学性质.计算结果表明,弛豫后氧空位Vo缺陷发生迁移.在外电场的作用下,填隙Zn离子向界面处偏移,界面能在电场强度超过0.1 V/Å后快速升高,界面之间的相互作用力变大,层间距减小,体系导电性迅速增强.采用差分电荷密度、功函数以及Bader电荷分析方法,计算出了界面处的势垒高度,证实了内建电场是ZnO压敏电阻具有非线性伏安特性的重要原因.采用态密度分析的方法,分析了原子轨道能级、陷阱能级以及能隙等微观参数对ZnO压敏电阻宏观导电性能的影响.本工作通过调控外电场的强度对含有缔合缺陷的ZnO/β-Bi2O3界面不同电气参数进行分析,为理解和调控ZnO压敏电阻的电学特性提供了新的思路.

1 引言

近年来,随着电气工程和电子学的快速发展,对供电可靠性的要求也越来越高,据研究表明,电力系统中大多数事故是由雷电引起的过电压造成的[1−3],因此过电压及其防护成为当今电力系统重点研究解决的问题之一.ZnO压敏电阻作为避雷器的核心元件,其具有优异的非线性伏安特性和浪涌吸收能力,在线路工作电压时呈现高阻态,不影响线路的正常运行,而在承受过电压时能迅速降为低阻态导通,可以有效限制过电压,吸收过电压带来的高能量,对电力系统的安全运行起到至关重要的保护作用.随着特高压电网的建设,传统的避雷器已经不能很好地满足当下特高压电网对过电压防护的要求,极大地影响了电力系统安全、稳定、可靠运行,避雷器的性能亟待提高[4].

ZnO压敏电阻内部的微观结构和晶界性质决定了其相关宏观电气特性[5].目前对ZnO压敏电阻导电机理的研究主要集中于宏观实验,通过在压敏电阻中掺杂诸如Bi,Mn,Cr,Zr,Sb,Si等不同元素的金属氧化物的方法,使ZnO压敏电阻内部形成错位、取代、填隙等结构缺陷,从而达到改善ZnO压敏电阻某些特性或使其具有新特性、新功能的目的[6−11].但因为实验原料、成分配方和工艺条件与宏观电气性能参数之间具有非常复杂的关联关系,精确的结果必然是基于大量的实验时间和资源的浪费上,这样机械化的研究方式势必会导致研究效率低下且缺乏合理的理论解释[12].由于晶界层的结构决定着ZnO压敏电阻的特性[13],因此从ZnO压敏电阻微观分子结构的角度出发,运用第一性原理对ZnO压敏电阻内晶界层进行研究,从更深层次对ZnO压敏电阻的电学机理进行探讨不免是一个新的研究方法.

本文建立了含有缔合缺陷的ZnO/β-Bi2O3界面模型,从体系的结构、能量、差分电荷密度、功函数、Bader电荷分析以及态密度等角度,对界面的导电性、内建电场、非线性伏安特性等相关电学性能进行了详细分析,对相关实验结果做出理论解释,为制造出性能更加优异、可靠性更强的ZnO避雷器提供坚实的理论基础.

2 模型的建构及计算方法

2.1 构建含有缔合缺陷的ZnO(002)/β-Bi2O3(210)界面模型

据Onreabroy等[14]的研究发现,当 ZnO 压敏电阻中以β相和δ相Bi2O3为主要成分时,其非线性伏安特性更为优异.通过TEM发现ZnO (002)与β-Bi2O3(210)存在实际的晶界面.徐彭寿等[15]指出任何实际应用的晶体均存在缺陷,且在ZnO晶体中以O空位和Zn填隙两种缺陷较为常见.因此本文以含有Zn填隙与O空位缔合缺陷的ZnO(002)/β-Bi2O3(210) 界面作为研究对象,对含有该缔合缺陷界面的电学特性进行研究.

如图1所示,紫色球代表Bi原子,红色球代表O原子,灰色球代表Zn原子.为了得到含有缔合缺陷的ZnO/β-Bi2O3界面,首先通过计算确定了6层ZnO(002)与6层β-Bi2O3(210)层片来构建不含有缺陷的晶界面,接着对界面进行ZnO缔合缺陷处理并进行结构优化[14,16−20].详细的模型建立步骤如下:对ZnO与β-Bi2O3晶胞分别进行结构优化,并对优化后的晶胞结构进行切割处理,得到ZnO(002)与β-Bi2O3(210).由文献[17]可知,以Zn为终端的ZnO表面能小,形成的界面较O为终端的稳定性好,因此模型采取以Zn原子为终端的ZnO表面与实际更为相符.在此基础之上构建含有缔合缺陷的晶界层结构.对结构的层数按如下公式进行测试计算:

图1 含有缔合缺陷的ZnO(002)/β-Bi2O3(210)界面初始模型Fig.1.Initial model of ZnO(002)/β-Bi2O3(210) interface with aggregation defects.

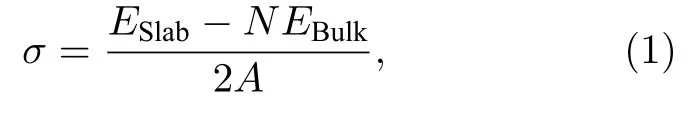
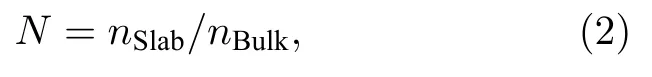
其中,σ代表表面能,ESlab是层片的能量,EBulk表示单胞的能量,N可用(2)式求得,nSlab与nBulk分别表示层片的原子个数与单胞的原子个数.

经计算,ZnO层片与β-Bi2O3层片的表面能在原子层数为6层时收敛于0.809和1.161 J/m2,因此分别选取6层来构建该界面模型能够满足模拟计算的要求.界面之间的间距也需要通过计算确定,界面层间距收敛测试数据如图2所示,结果表明,界面间距约为2.06 Å时存在最小的界面能量,因此选择2.06 Å的界面间距是合理的.在构建界面模型中,晶格匹配同样是不容忽视的因素之一,一般来说,晶格失配度应在5%以下,如果界面结构的晶格失配度过高,则界面结构会由于应力过大而不能稳定存在,本文所构建的界面结构的晶格失配度如表1所列,表1中U和V分别代表晶胞的长与宽,由表1可知,最大晶格失配度为3.16%,符合界面构造规律.

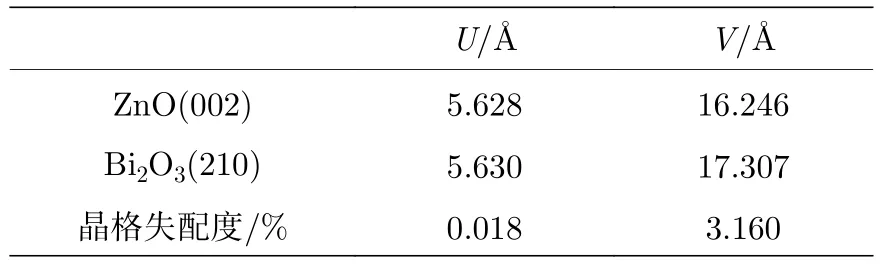
表1 界面结构晶格失配度Table 1.Interfacial structure lattice mismatch.

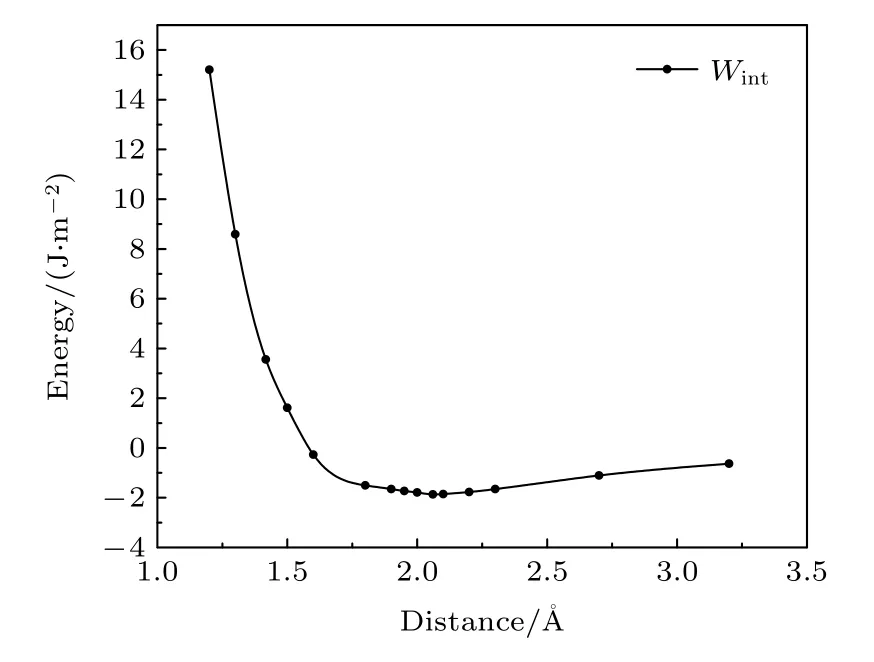
图2 界面层间距收敛测试数据Fig.2.Convergence of interfacial layer spacing test data.

为了模拟含有缔合缺陷的ZnO/β-Bi2O3界面,在尽可能靠近界面处添加一个锌离子并去除一个氧原子.为了避免z方向相邻两层片的相互作用,在结构的两侧共选取了20 Å的真空层来消除影响.该界面结构能相对精确地描述实际ZnO压敏电阻的内部微观情况.

2.2 计算方法

采用基于密度泛函理论 (DFT) 的VASP (Viennaab initiosimulation pack-age) 软件包对晶体结构进行优化和电子结构计算.在广义梯度近似(GGA)的框架下利用PBE (Perdew-Burke-Ernzerhof)泛函来描述电子交换和相关势,离子实和价电子之间的相互作用通过投影缀加平面波(projectoraugmented wave,PAW)方法进行描述.用于电子波函数平面波扩展的能量截断值设置为450 eV,布里渊区取样采用Monkhorst Pack方法产生的4×1×1k点网格用以几何优化,能量和力的收敛判据分别为1 × 10–5eV/atom和0.02 eV/Å.

3 结果与讨论

3.1 外电场对界面结构和能量的影响

用GGA方法对具有缔合缺陷的ZnO/β-Bi2O3界面进行优化,得到具有最低能量的优化结构如图3所示.在界面结构的ZnO 侧,Zn31为填隙锌离子,Zn24与Zn29是处于界面处且临近Zn31的锌原子,与Zn6,Zn7,Zn11,Zn12共同连接的氧原子缺失而形成氧空位.含有缺陷的ZnO/β-Bi2O3界面经优化后,Zni周围的锌原子与氧原子稍微向内弯曲,这是因为Zni与周围的锌原子有很强的共价键,同时Zni的正电势场会使处于其周围的氧原子在电磁作用的影响下向Zni处偏移.处于β-Bi2O3侧的O36发生界面迁移,导致Vo发生了反方向的界面转移,在β-Bi2O3侧的Bi1,Bi9,Bi12处形成新的Vo,这是因为在ZnO中锌填隙缺陷形成焓要低于氧空位缺陷形成焓,且氧化锌中锌原子的原子半径低于氧原子[15],所以在ZnO表面更容易形成锌填隙缺陷,同时受到表面悬挂键的影响,这使得界面和界面附近原子在满足收敛条件下,处于β-Bi2O3侧的O36受静电力的影响而发生跃迁,在β-Bi2O3侧形成新的Vo.由于Vo而形成的正电势场和力学势场,使得处于Vo周围的Bi1与Bi9,Bi12会受到电磁作用和结构力场的影响而向Vo处偏移.

图3 含有缔合缺陷的ZnO(002)/β-Bi2O3(210)界面优化模型Fig.3.Optimization model of ZnO(002)/β-Bi2O3(210) interface with aggregation defects.

为了研究含有缔合缺陷的ZnO/β-Bi2O3界面在不同电场强度下结构以及能量的变化情况,本文沿着z轴正方向以0.05 V/Å为步长,对界面结构施加0—0.25 V/Å的电场强度,并分别对其进行结构优化,分析界面结构的几何构型变化.结果表明,在β-Bi2O3侧新形成Vo附近的原子会随着电场的加强而更加偏向于Vo中心,外加电场会使Vo处电磁作用的影响更加明显,ZnO侧的填隙锌离子会在电场的作用下逐渐向界面方向移动.下文差分电荷密度图以及Bader电荷分析中可以看出,填隙锌离子在向界面移动的过程中会捕获电子,陷阱不断填充,致使ZnO压敏电阻的肖特基势垒发生畸变,这也是导致ZnO压敏阀片老化的原因之一[21,22].值得注意的是,外加电场在0—0.1 V/Å范围内时,界面结构并未发生明显的变化,而在0.1—0.25 V/Å的电场作用下,结构变化明显,平均层间距减小,界面的导电性增强.

界面之间结合的强弱对材料的宏观性能有重要的影响[22].界面能是衡量界面之间相互作用力的重要参数,反映了自由表面结合形成界面过程中能量的释放,界面能越小则在结合成界面的过程中释放的能量越大,不同界面之间的相互作用力也就越大,界面之间结合得更加紧密.可用下面公式来计算界面能:

图4是不同电场下界面能的变化曲线,外电场强度在0—0.1 V/Å时,ZnO/β-Bi2O3界面能变化幅度较小,表明在该阶段界面的结合能力基本不变.当场强超过0.1 V/Å 后,体系的界面能显著降低,尤其在施加0.15 V/Å的电场时,界面能以更快的速度下降,界面的结合力大幅度升高.

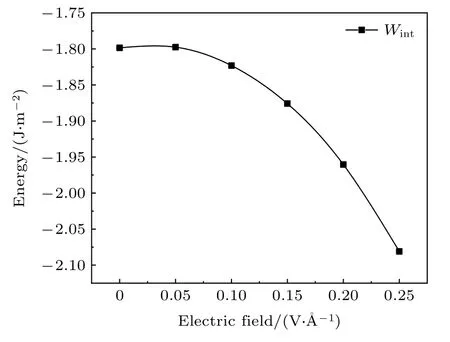
图4 ZnO/β-Bi2O3界面能Fig.4.Interface energy of ZnO/β-Bi2O3.

晶界主要依靠分子中导带上的自由电子与价带中的空穴运动进行导电,HOMO能级上对应的能量越高表明电子越容易跃迁,因此,可以用HOMO能级上对应能量的高低来反映材料的导电性能,ZnO/β-Bi2O3体系HOMO与LUMO能级能量随电场变化如图5所示.

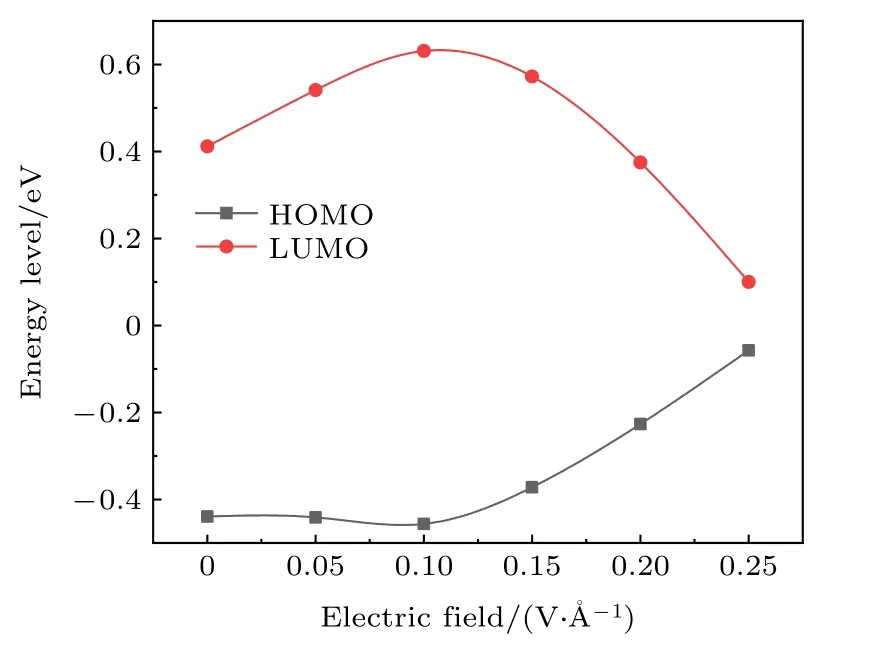
图5 ZnO/β-Bi2O3体系HOMO与LUMO能量Fig.5.HOMO and LUMO energy of ZnO/β-Bi2O3.

由图5可知,当电场强度在0—0.1 V/Å之间时,HOMO能级上的电子能量略有降低,LUMO能级能量持续升高,LUMO与HOMO之间的宽度增加,表明界面的导电性稍有减弱,电子更难发生跃迁,结合上述对ZnO/β-Bi2O3体系在该电场范围内界面能的分析,从宏观上来看,ZnO/β-Bi2O3体系在此电场强度区间处于预击穿区,ZnO压敏电阻能够稳定地在这一区域工作,伏安特性曲线接近线性化.当电场强度超过0.1 V/Å后,HOMO能级的电子能量增加,LUMO随着电场强度的增加而减小,LUMO与HOMO之间的禁带宽度迅速减小,尤其是当电场强度超过0.15 V/Å以后,HOMO能级的电子能量和禁带宽度变化的速度更快,使得HOMO能级上的电子更容易跃迁至导带上,由价电子变成自由电子,且界面间的相互作用显著增加,层间距缩小,材料的导电性能迅速增加.在宏观上称此阶段为击穿区,这里所提及的击穿并不是一般介质的破坏击穿,而是指当ZnO压敏电阻所承受的电压超过某一个数值以后,ZnO压敏电阻的阻值急剧下降的现象[22,23].在这一区域中的伏安特性曲线呈非线性特征,且随着外加电场的不断增大,HOMO能级上的电子能量也随之增大,价电子获得的能量不断增强,使电子的迁移变得愈发容易.综合图4和图5的数据可以得出,ZnO/β-Bi2O3体系的击穿场强在0.15 V/Å附近,一般ZnO压敏陶瓷单晶界击穿电压为2.5—3.6 V之间[24],通过TEM观察到非晶区晶界宽度为1—2 nm[14],因此可求得实际单晶界击穿场强在0.12—0.36 V/Å之间,进一步说明本文所构建的界面模型能够较好地反映实际ZnO压敏阀片的内部微观结构.

3.2 不同外电场对界面内建电场的影响

3.2.1 差分电荷密度分析

为了定量分析不同外电场对界面内建电场的影响,本文分别对外加电场强度为0,0.1以及0.25 V/Å时界面附近的差分电荷密度、电荷转移量以及肖特基势垒高度进行具体研究.图6(a)—图6(c)为计算得到的电场强度分别为0,0.1及0.25 V/Å时的界面差分电荷密度图.图6(a)中黄色区域代表电子的聚集,蓝色区域表示电子的损失,可以看出在ZnO和β-Bi2O3组成界面后,层片的电子发生重排,集聚于β-Bi2O3层片与界面处,且β-Bi2O3层片中的O原子与Bi原子周围电子的局域性分布明显,显示出较强的离子键.界面处可以看出ZnO层片中的Zn原子与β-Bi2O3层片的中O原子存在明显的电荷转移,电子由ZnO层向β-Bi2O3层发生转移,形成一个由ZnO层片指向β-Bi2O3的内建电场.在图6(b)中,施加0.1 V/Å的电场后,与未加电场时的差分电荷密度相比,电子之间的交互由β-Bi2O3层更多地聚集到界面处,且电子的运动更为活跃.通过后文对Bader电荷的分析不难看出,ZnO层向β-Bi2O3层转移的电子数达到最大值,内建电场强度增强,ZnO层内部向界面处注入电子的速率与界面向β-Bi2O3层转移电子的速率也达到一个平衡,结合前文分析知该电场强度对应开始放电击穿前的状态.随着外电场的持续增大,如图6(c)所示,在高电场能量的驱动下,电子在界面处的聚集更加明显,ZnO层的Zn原子与β-Bi2O3层的O原子成键性增强,靠近界面处的ZnO层与β-Bi2O3层之间产生强烈的相互作用,与前文界面能大幅度下降的分析相符.因此,在该电场强度下更容易形成空间电荷的聚集,并与界面中存在的陷阱相结合,导致内建电场强度降低,对电子的束缚能力减小,电子的跃迁难度下降,导电性能增强,层片更易于击穿.

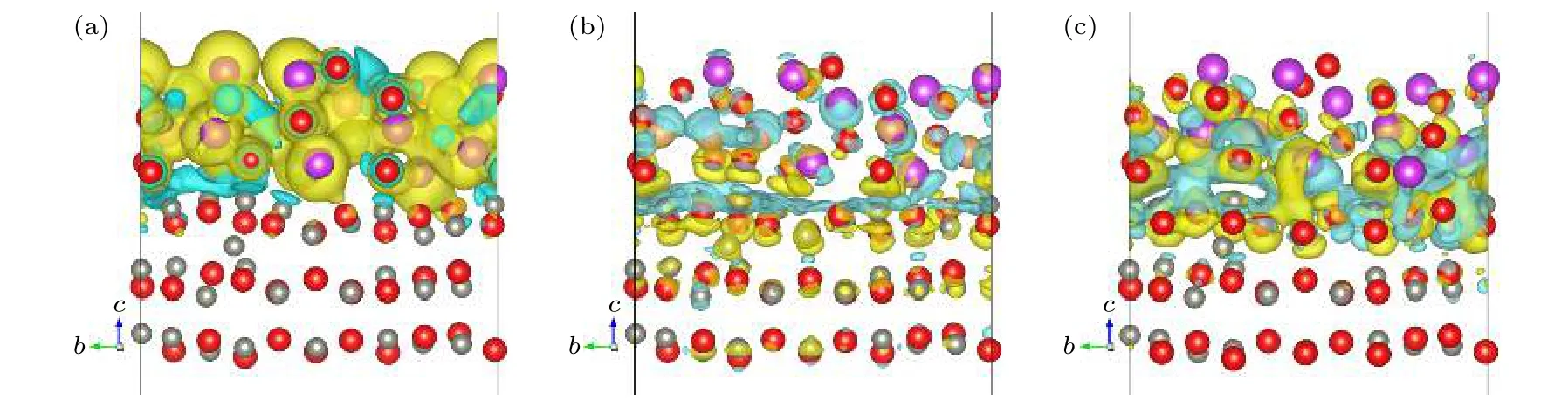
图6 差分电荷密度 (a) 电场强度为0 V/Å;(b) 电场强度为0.1 V/Å;(c) 电场强度为0.25 V/ÅFig.6.Differential charge density:(a) Electric field strength is 0 V/Å;(b) electric field strength is 0.1 V/Å;(c) electric field strength is 0.25 V/Å.

3.2.2 Bader电荷分析

Bader电荷分析方法是基于实空间划分的计算原子电荷的方法.该电荷分析方法将电子密度零通量面称为原子间的分界面,将每个被划分出的原子独立空间称为原子盆,满足∇ρ(r′)·n(r′)0 的条件,式中r′为原子界面上的任意点,n为界面上的单位法矢量,ρ是电子密度函数[25].这样的空间划分相较于其他方法而言,具有更加严格的物理解释,并且理论意义也更加明确.原子电荷可用以下公式求得:

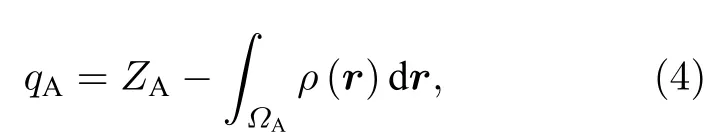
式中ΩA代表A原子盆,ZA代表A原子盆核电荷数.

对界面中的原子进行Bader电荷分析,正值意味着失去电子,负值意味着得到电子.表2列出了界面中不同原子的电子分别在电场强度为0,0.1及0.25 V/Å时的转移情况.

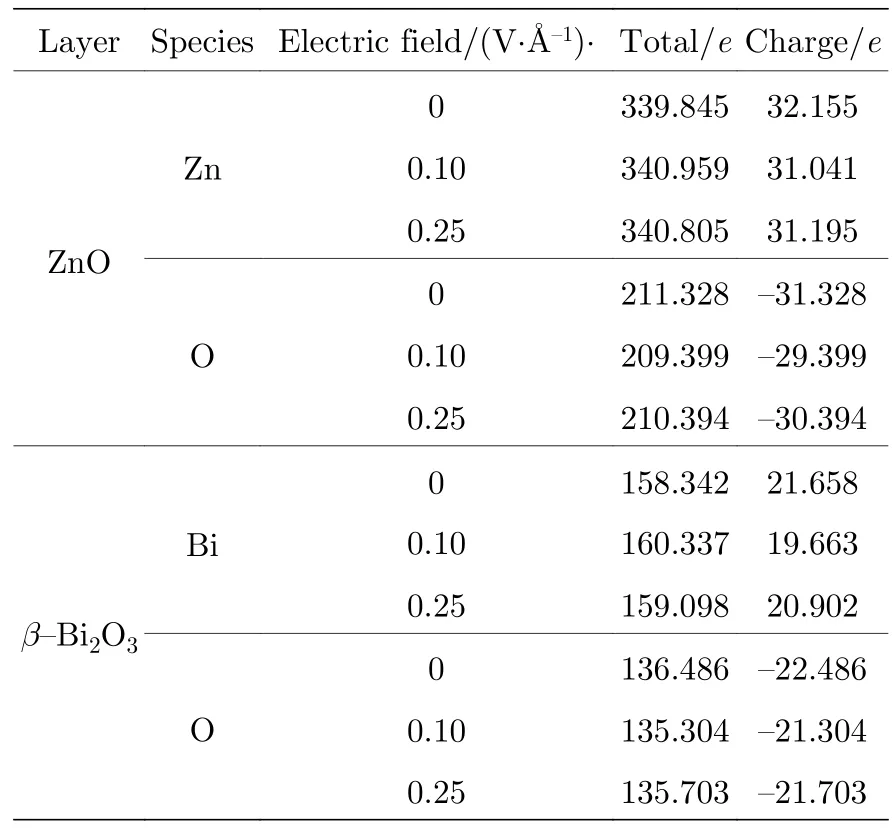
表2 不同电场下Bader电荷分析Table 2.Bader charge analysis with different electric fields.

由表2可以看出,当ZnO与β-Bi2O3组成晶界层后,ZnO层的电子减少,空穴产生,而β-Bi2O3层的电子增加,空穴数量减少.电荷在界面发生了重新排布,使界面附近产生了电子-空穴对和内建电场.由表2可知,基态ZnO层片向β-Bi2O3层片转移0.827e,证明在ZnO与β-Bi2O3组成的界面之间有一个方向由ZnO层片指向β-Bi2O3层片的内建电场.当电场强度为0.1和0.25 V/Å时,ZnO层片向β-Bi2O3层片转移分别转移1.642e和0.801e.在0.1 V/Å的电场强度下,ZnO层片向β-Bi2O3层片转移电子数最多,内建电场强度达到最大值,界面中的电子更难以跃迁,导电性能降低.继续增加电场强度至0.25 V/Å后,在外电场的驱动作用下,更多的电子得以注入界面,形成空间电荷的聚集并与处于空态的陷阱结合,势必会使ZnO层片向β-Bi2O3层片转移电子数降低,内建电场强度降低,使电子跃迁更加容易.在该电场强度下,界面被外部电场击穿发生导通,导电性增强,外电场的能量能通过界面迅速释放.这进一步说明内建电场与材料导电性的关系是材料呈现非线性伏安特性的重要原因.

3.2.3 肖特基势垒分析

为了定量表示内建电场与外电场之间的关系,可以用Schottky势垒高度来进行描述[26,27].对于典型的金属与n型半导体接触而言,Schottky势垒可用以下公式表示:

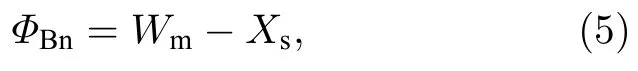
式中Wm为金属的功函数,Xs为半导体的电子亲合能.由于本文中的ZnO层厚度远远小于胞体内部空间电荷形成区,所以仅需要考虑ZnO层与β-Bi2O3层接触形成的空间电荷区,可以认为ZnO和β-Bi2O3组成界面产生的电势差全部作用于ZnO与β-Bi2O3之间,在ZnO与β-Bi2O3的各自表面和晶粒内部之间是不存在电势差的[28].对(5)式进行改写,可知此时n型半导体与p型半导体的肖特基势垒的公式如下:

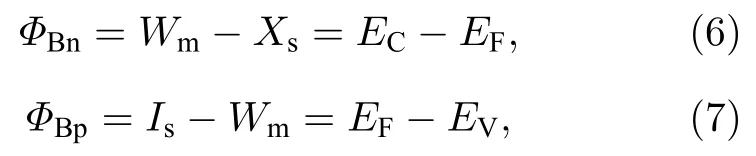
式中,EC表示导带底所处能级,EF为Fermi能级,EV代表价带顶所处能级.从前文中的讨论可知,ZnO与β-Bi2O3组成的界面为n型Schottky接触,而在外加电场的作用下,自0.05 V/Å起变化为p型Schottky接触,因此根据n型及p型Schottky接触的公式可求出在不同电场强度下界面的Schottky势垒高度,如图7所示.从图7可以看出,Schottky势垒高度随电场变化可分为三个阶段,第一个阶段在0—0.05 V/Å电场范围内,Schottky势垒高度随电场强度的增大逐渐增大,该阶段由于外电场的影响,原来的平衡态被打破,界面中处于定域态的电子在外电场的驱动下从陷阱内脱陷,于是界面中的陷阱会由占据态变为空态,陷阱能级随之降低,界面中电子数目增多,内建电场逐渐加强,电子需克服的Schottky势垒高度变高.在0.05—0.15 V/Å电场下进入第二阶段,此时陷阱中的电子在外电场的作用下全部脱陷,陷阱能级达到最低点,Schottky势垒高度在0.1 V/Å电场强度下达到最大值.随着电场的进一步增大,外电场对电子的驱动超过了内建电场对电子转移的抑制作用,于是在晶界层中形成大量空间电荷,使更多的陷阱被占据,占据态陷阱能级不断上升,同时内建电场也因为电子的入陷而减小,高强度电场也使镜像力对Schottky势垒的影响愈发明显[29],于是Schottky势垒高度会较之前以更快的速度下降,最终会随着电场强度的不断升高,使晶界内的陷阱全部填满而导致晶界击穿.计算得到的Schottky势垒高度变化趋势与成鹏飞等[29]实验得出的Schottky势垒高度变化趋势相符得很好.

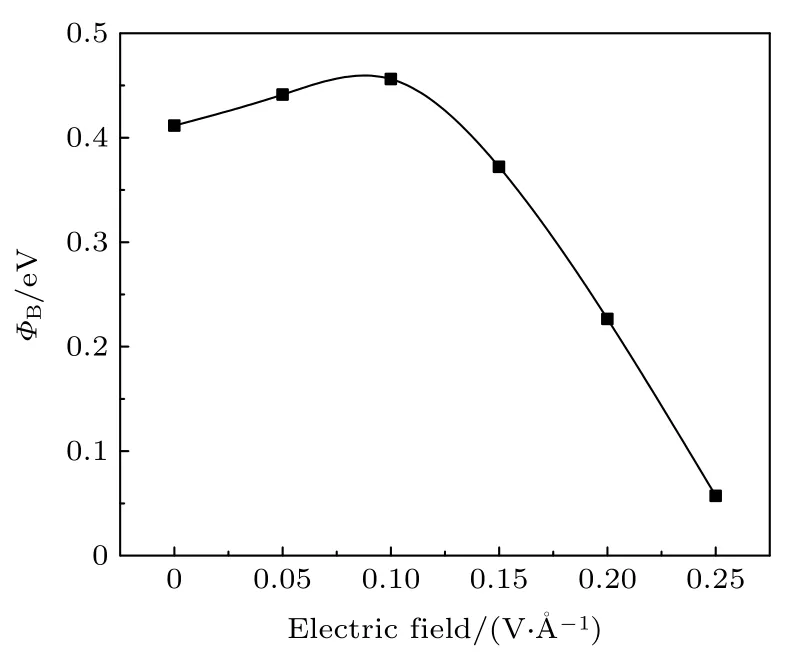
图7 界面的肖特基势垒高度Fig.7.Schottky barrier height of the interface.

内建电场形成的根本原因可概括为ZnO与β-Bi2O3各自的Fermi能级不同,而在两者形成界面后,载流子必然会在界面中扩散来使两侧的Fermi能级相等,从而达到一个稳定的状态.由图8可知,ZnO的平均功函数小于β-Bi2O3的平均功函数,驱动电子从ZnO层片向β-Bi2O3层片转移,因此在界面处形成具有一定宽度的空间电荷区.在施加强度为0.25 V/Å的电场后,β-Bi2O3层片的平均功函数曲线相较于0 V/Å时的曲线有所下偏,而ZnO层片的平均功函数曲线有一定程度上升.功函数的计算公式为

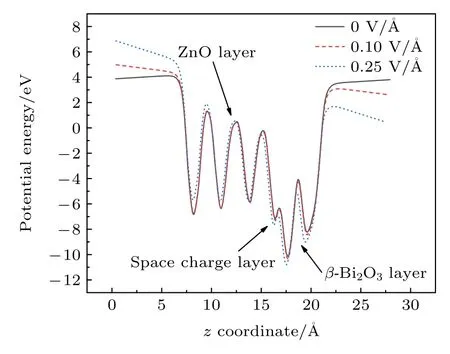
图8 沿着z轴方向的平均功函数Fig.8.Average work function along the z axis.

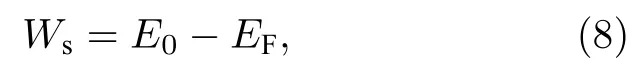
式中E0代表真空能级.由(8)式可知,ZnO和β-Bi2O3的Fermi能级分别向禁带中央移动,使得两者的Fermi能级之差减小,内建电场强度降低.综合以上对肖特基势垒和界面功函数的分析,可知界面中内建电场的存在是ZnO压敏电阻具有良好非线性特性的关键因素.

3.3 不同外电场下界面的态密度

图9(a)绘制的是未加外电场ZnO/β-Bi2O3界面的总态密度和分波态密度,从图中可以看出,价带分布在–19.89—0 eV能级区间,其中第一价带位于–19.89—–16.07 eV价带区域,该峰宽度较窄,局域性很强,主要由O 2s轨道贡献,属于深能级处的轨道相互作用.第二价带位于–11.54—–8.02 eV,主要由Bi 6s轨道以及O 2p轨道贡献,从分波态密度可以看出Bi 6s轨道与O 2p轨道存在态密度“共振”,说明该区域存在s-p杂化现象,属于成键能级区域.在–7.86—0 eV能量区域内存在两个高密度态分布,峰值对应的能量分别为–5.68和–2.16 eV,该区域主要由Zn 3d轨道与O 2p轨道贡献,且根据分波态密度图来看,Zn 3d轨道与O 2p轨道同样存在态密度的“共振”现象,有较强的成键性,且存在p-d杂化.由于缔合缺陷的引入,与纯ZnO/β-Bi2O3界面的态密度相对比[17],存在缺陷界面的态密度曲线在带隙之间出现了陷阱能级,在Fermi能级附近出现了由Zn 4s轨道和O 2p轨道贡献的施主能级,距导带底约0.33 eV.位于导带区域的能级主要由O 2p轨道和Bi 6p轨道组成,分布在0—7 eV区域内.

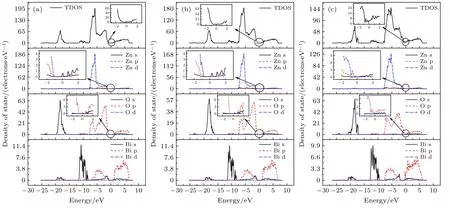
图9 界面的态密度和分波态密度 (a) 电场强度为0 V/Å;(b)电场强度为0.1 V/Å;(c)电场强度为0.25 V/ÅFig.9.Interface density of states and partial density of states:(a) Electric field strength is 0 V/Å;(b) electric field strength is 0.1 V/Å;(c) electric field strength is 0.25 V/Å.

图9(b)是施加0.1 V/Å电场时的总态密度和分波态密度,界面的总态密度和分波态密度曲线相较于基态而言,价带区域并没有明显的变化.位于带隙中的陷阱能级向远离导带底方向发生偏移,移动后距导带底约0.39 eV.处于导带区域的O 2p轨道与Bi 6p轨道向右移动,使得共价键成键增强,能级增大,价带顶与导带底之间的距离增大.该结果表明,在0.1 V/Å外加电场的作用下会使占据态陷阱变为空态,电子的脱陷造成陷阱能级向深能级方向移动,载流子浓度增大,内建电场强度也因此升高,对电子跃迁抑制作用增强,致使界面的导电性减弱.图9(c)是在施加0.25 V/Å的电场时总态密度和分波态密度,由于Stark效应的影响[30,31],原子在外加电场的作用下能级会发生分裂,造成能级的移动,对应轨道的能级变宽.位于价带区域的O 2p,O 2s,Zn 3d和Bi 6s均向右偏移,能级升高.位于能隙中的陷阱能级向左移动,穿过Fermi能级成为完全占据态的施主能级.导带处的O 2p轨道和Bi 6p轨道向Fermi能级处偏移,使得O与Bi原子间的共价键成键减弱,带隙宽度降低.上述结果表明,在该外加电场的作用下,界面中的陷阱捕获空间电荷而重新恢复占据态,使自身能级得到提高,界面之间电子交换数量减少,更多的在各自层片中进行电子交换,内部电场强度降低,外层电子的跃迁难度降低.从TDOS曲线可以看出,该界面已处于击穿状态,界面的导电性增强.

4 结论

本文采用密度泛函理论对不同外加电场下ZnO/β-Bi2O3界面的相关电学特性进行了研究,建立了相对精确的界面模型,并对其结构和能量进行分析,揭示了不同电场强度对界面中内建电场的影响,从态密度的角度分析了外电场对能带带隙的调控机制,得到以下结论.

1)界面中锌填隙Zni与氧空位Vo缔合缺陷的存在,会使得周围的原子向缺陷中心偏移,使结构发生变化,并在外电场的作用下,平均层间距有明显的减小,使得界面导电能力提高.

2)电场强度为0—0.1 V/Å时,界面间结合能力基本不变,LUMO能级对电场敏感,随着电场的增大而增大,HOMO能级略微有减小,导带处的O 2p轨道与Bi 6p轨道相较于基态而言均向右偏移而价带区域并没有明显的变化,陷阱能级向深能级偏移,占据态陷阱变为空态,带隙增大,导电性减弱.在0.1—0.25 V/Å电场作用下,LUMO能级随电场的增大而减小,HOMO能级随电场的增大而迅速增大,两相界面之间的相互作用大幅度增强,价带区域与导带区域对应的轨道均向低能级偏移,陷阱能级上升,空态陷阱与空间电荷结合变为完全占据态,带隙明显减小,导电性能增大,界面的击穿场强约在0.15 V/Å附近.

3) ZnO层片中Zn原子出现电子的缺失,β-Bi2O3层片中O原子出现电子的聚集,形成由ZnO层片指向β-Bi2O3层片的内建电场.在外电场的作用下,ZnO层片向β-Bi2O3层片电子转移在0.1 V/Å电场时达到顶峰,转移电荷1.642e,在电场强度增加至0.25 V/Å时,转移电荷减少到0.801e,肖特基势垒高度呈现先增大后减小的趋势.阐述了内建电场与导电性的关系是材料呈现非线性伏安特性的重要原因.