基于冷原子重力仪的绝对重力动态移动测量实验*

程冰 陈佩军2) 周寅 王凯楠 朱栋 楚立 翁堪兴王河林 彭树萍 王肖隆 吴彬† 林强‡

1) (浙江工业大学理学院,浙江省量子精密测量重点实验室,杭州 310023)

2) (黄山学院机电工程学院,黄山 245041)

动态重力测量可以提高重力场的勘测效率,对基础地质调查、资源勘探、地球物理研究等具有十分重要意义.本文基于冷原子重力仪、惯性稳定平台和牵引动力装置搭建了一套绝对重力动态移动测量系统,并开展了绝对重力动态测量实验.首先测量了不同牵引速度下的垂向振动噪声功率谱,理论分析了其对动态重力测量的影响;其次评估了不同牵引速度对原子干涉条纹对比度和直流偏置量的影响,分析了动态环境下的振动补偿效果;在最大牵引速度为5.50 cm/s、最大振动幅度为0.1 m/s2的情况下,实验上仍能基于振动补偿技术恢复原子干涉条纹.在此基础上,通过开展不同T下的原子干涉条纹测量,评估了动态测量环境下的绝对重力值,在校正完系统误差并减去绝对重力初始值后得到的测量结果为(–1.22±2.42) mGal (1 Gal=0.01 m/s2).最后,通过与静态环境下的绝对重力测量值进行比较,发现两者基本吻合.本文开展的绝对重力动态移动测量实验有望为车载动态绝对重力测量提供数据参考.

1 引言

随着激光技术、原子冷却及相干操纵技术的迅猛发展,冷原子干涉仪逐渐成为精密测量领域的一种有效工具,在基础物理研究[1−3]和应用技术开发[4−6]方面都发挥了十分重要的作用.基于冷原子干涉仪的加速度计[7]、陀螺仪[8,9]、重力仪[10,11]等新型惯性传感器具有灵敏度高、稳定性好、漂移小等特点,因此受到越来越多的关注.尤其是冷原子重力仪在近些年得到快速发展,其测量灵敏度[12−14]和精度[15,16]可以与经典最好光学干涉式绝对重力仪相媲美,在测量重复率、长期连续测量方面还具有独特优势.经过技术的更新与迭代,冷原子重力仪的小型化、轻量化和工程化得到改善[6,17−20].通过参加国际重力比对,冷原子重力仪的绝对重力测量精度逐渐得到验证[21,22];通过在地震台站开展连续重力观测实验,其长期稳定性和环境适应性得以证实[4];通过野外环境下的车载移动定点绝对重力测量实验,其外场适应能力及性能得到检验[23,24].越来越多的实验证据表明,冷原子重力仪有望成为下一代的高精度绝对重力测量仪器,未来可服务于重力基准维护、地球物理研究、基础地质调查等领域.

然而,目前大多数冷原子重力仪只能定点静态工作,且其实验装置仍十分复杂.动态环境下的重力测量对仪器的体积、重量、功耗及抗振动干扰能力要求较高,且需要解决动态环境引入的横纵摇摆、垂向振动叠加、水平加速度串扰等一系列问题,因此绝对重力加速度的动态测量一直是一个难题.虽然基于原子干涉仪的动态测量实验也有先前文献报道[25−27],但前期大多是验证性研究.近几年,法国的Bidel等[28,29]首次基于惯性稳定平台和小型化冷原子重力仪搭建了一套绝对重力动态测量系统,并在船载和机载环境下开展了动态测量实验,重力测量的分辨率分别优于1 mGal (1 Gal=0.01 m/s2)(船载)[28]和1.7 mGal(机载)[29].这些实验结果为动态绝对重力测量提供了新的思路,为未来重力测绘、重力匹配导航、资源勘探提供了一种新的技术方案.绝对重力动态移动测量实验有望为车载动态绝对重力测量提供参考,车载绝对重力动态测量相比船载和机载,其振动频谱及测量工况更为复杂,难度较大.然而,车载动态重力测量可以提高陆域重力场的勘测效率,在作业复杂度、空间分辨率、机动性等方面具有一定优势.

本文报道了我们课题组在绝对重力动态移动测量方面的研究进展.基于冷原子重力仪、惯性稳定平台和牵引动力装置,我们搭建了一套绝对重力动态测量系统,并开展了动态测量实验.测量了不同牵引速度下的垂向振动噪声功率谱,分析了其对绝对重力测量性能的影响.此外,我们还研究了不同牵引速度对原子干涉条纹各参数的影响,进而开展了动态环境下的振动补偿技术研究,获取了动态环境下的绝对重力数据.本文的实验研究为车载动态绝对重力测量提供了前期验证.

2 动态绝对重力测量的基本原理

冷原子重力仪的基本原理(三拉曼脉冲原子干涉仪)在很多文献[14,30,31]中都有介绍,本文不再详述.基于冷原子重力仪的动态重力测量的关键是振动补偿,我们在先前的文章中也有简要介绍[32],其基本原理如图1所示.经过三个拉曼脉冲(π/2-ππ/2)作用后,原子物质波发生干涉,在探测区利用归一化荧光探测法获取F=1态和F=2态上的原子布居数,利用探测激光照射冷原子团,原子团自发辐射出荧光,通过光电管接收荧光信号,得到的原子布居数信号P可以表示为:

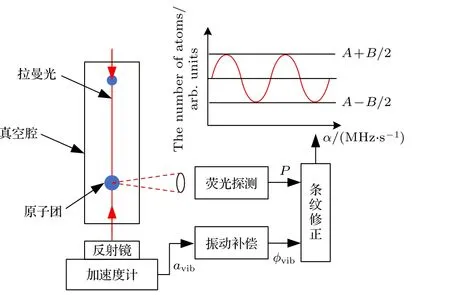
图1 动态绝对重力测量的原理示意图Fig.1.The schematic diagram of dynamic measurement of the absolute gravity.

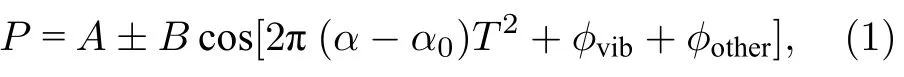
其中,A,B分别是原子干涉条纹的直流偏置和幅度,α为拉曼光扫频的啁啾率,α0为当地绝对重力值对应的啁啾率,T为两束拉曼光脉冲之间的时间间隔,φvib为振动加速度噪声产生的干扰相位,φother为其他噪声源引起的干扰相位.静态环境下,因φvib,φother的相位幅度不大,可以通过扫描α得到原子干涉条纹,通过提取干涉条纹的相位,基于下式可以得到重力加速度信息[10,17]:

其中,keff为拉曼光的有效波矢,keffk1−k2是两束反向拉曼光束的矢量合成波矢,用于提高原子团的受激拉曼跃迁效率.

然而在动态环境下,原子重力仪会受到外界强振动环境的影响,(1)式中的四个参数A,B,φother,α会发生随机波动,影响高精度重力测量;φvib的变化幅度将大于其他相位,因其幅度比较随机且往往大于一个条纹周期(0—2π),这时通常不能直接得到原子干涉条纹.

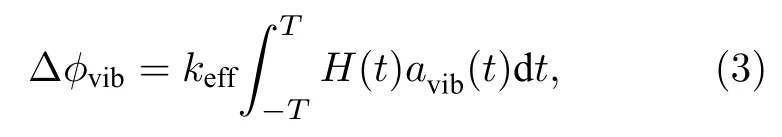
为了重新恢复出原子干涉条纹,并提取重力加速度信息.将文献[32]中的振动补偿方法与参数预测估计方法相结合,提出了一种新的动态迭代条纹拟合算法.下面进行详细介绍,与文献[32]相似,在拉曼反射镜下放置一个高精度加速度计(如图1所示),用于采集拉曼反射镜的实时垂向振动加速度信号avib(t) ;结合原子干涉仪的灵敏度函数H(t)[14],可以通过(3)式的积分实时计算出垂向振动相位φvib:鉴于计算原子布居数的其余4个参数(A,B,φother,α)均无法直接测量,采用参数预测估计方法进行估计和修正,算法的基本流程如图2所示.图中Ai,Ai+1为i和i+1时刻的直流偏置,Bi,Bi+1为i和i+1时刻的对比度,αi,αi+1为i和i+1时刻拉曼光扫频的啁啾率,为i和i+1时刻由其他噪声源引起的干扰相位,Pi为i时刻测量得到的原子布居数,为i时刻与i+1时刻原子布居数的预测值,该预测值可由(1)式计算获得,∂Pi为i时刻测量值与预测值的偏导数,kA,kB,kα,为4个参数A,B,α,φother的更新系数,为i时刻的垂向振动相位,为i时刻统一到一个条纹周期的振动相位,为振动补偿后的相对啁啾率.

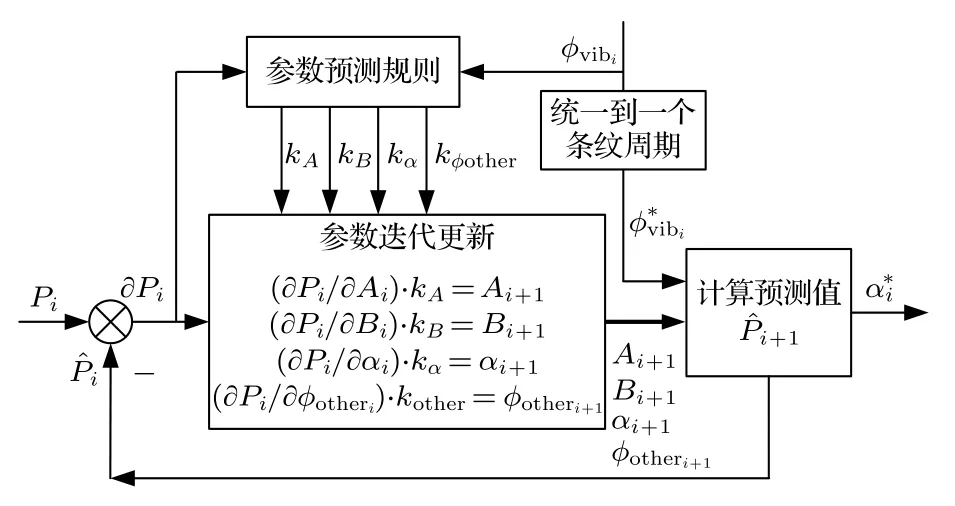
图2 动态迭代条纹拟合算法的原理示意图Fig.2.The schematic diagram of iterative fitting algorithm of the dynamic fringes.

动态迭代条纹拟合算法主要包括参数预测规则、参数迭代更新、计算预测值三个环节.在参数预测规则环节,由于动态绝对重力测量系统每扫描一次啁啾率αi便得到一个原子布居数Pi,结合i时刻的参数值并利用(1)式可计算出预测值Pˆi,并基于(4)式可求偏导∂Pi:

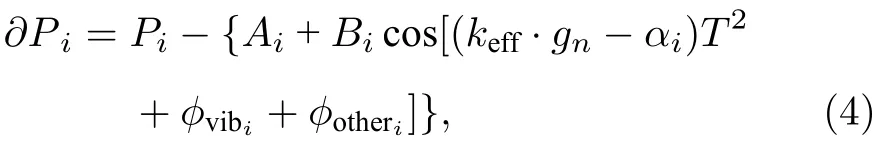
由于(1)式中4个参数的变化可通过原子布居数体现出来,同时垂向振动会影响量子重力仪系统的状态参数,因此我们制定参数预测规则时,把振动相位和原子布居数的偏导数作为规则的输入,kA,kB,kα,kφ作为规则的输出,预测规则使用了模糊集合规则.

首先把两个输入信号模糊化,用语言形式描述输入情况(负大、负中、负小、零、正小、正中、正大),根据经验制定模糊规则表,通过查表的方式得到输出的模糊值,采用加权平均的方法实现去模糊化,其中振动相位的权值大于原子布居数的权值.参数预测规则的输出信号分别与原子布居数的4个偏导数相乘得到下个时刻的参数更新值Ai+1,Bi+1,αi+1,,最后我们采用线性迭代更新的方法以弥补偶尔参数突变造成的影响.

然而,在动态测量环境下,振动相位往往大于一个条纹周期;为了能够拟合原子干涉条纹,需要先将振动相位归算到一个条纹周期之内以得到计算出下一时刻的原子布居数预测值,并计算相对啁啾率.最后通过多组[,Pi]数据拟合出原子干涉条纹,其中算法中各参数的初始值是根据测量得到的原子布居数分布范围评估得到.根据不同T下的原子干涉暗条纹情况,提取相应的中心啁啾率值以获取绝对重力值.该动态迭代条纹拟合算法可以减小动态环境下原子干涉条纹信号波动的影响,更适应动态测量,单点可以计算重力值,具有实时性、快速性、抗环境干扰等特点.

3 实验装置与实验步骤

为了开展绝对重力的动态移动测量实验,验证动态迭代条纹拟合算法的有效性,评估振动补偿技术的效果,我们搭建了一套基于小型化冷原子重力仪的可移动绝对重力测量系统,下面分别介绍整个实验系统及实验步骤.

3.1 绝对重力动态测量实验装置与温湿度环境

绝对重力动态测量系统的示意图、实物图和温湿度曲线分别如图3(a),(b)和(c)所示,整个测量系统由三个子系统组成:原子重力仪系统、惯性稳定平台系统、牵引动力系统.原子重力仪系统是整个重力测量的核心,主要进行绝对重力测量,原子重力仪主要由真空单元、光路单元和电控单元三部分组成,每部分的详细介绍可参考文献[32].惯性稳定平台系统主要用于维持原子重力仪的敏感探头(真空单元)始终处于垂线方向,它主要由惯性稳定平台和全球定位系统(global positioning system,GPS)组成,GPS放置在测试车间的外部以接收定位信息.为了开展振动补偿技术研究,真空单元中的拉曼反射镜被移动到外部,固定在一个高精度三轴加速度计上部,并与惯性稳定平台内框架的底部刚性固定.牵引动力系统使整个装置按照设定程序运动,它主要由导轨、推车、牵引电机组成.导轨固定在测试车间(一个工厂的机械加工及装配间)的地面上,总长度约为15 m,基本处于南北走向.推车坐落在导轨上,牵引电机利用钢丝绳拉动推车在导轨上做水平往复运动,运动速度可以通过编程进行调节.光路单元、电控单元和笔记本电脑放置在推车的前端,惯性稳定平台放置在推车的尾端.

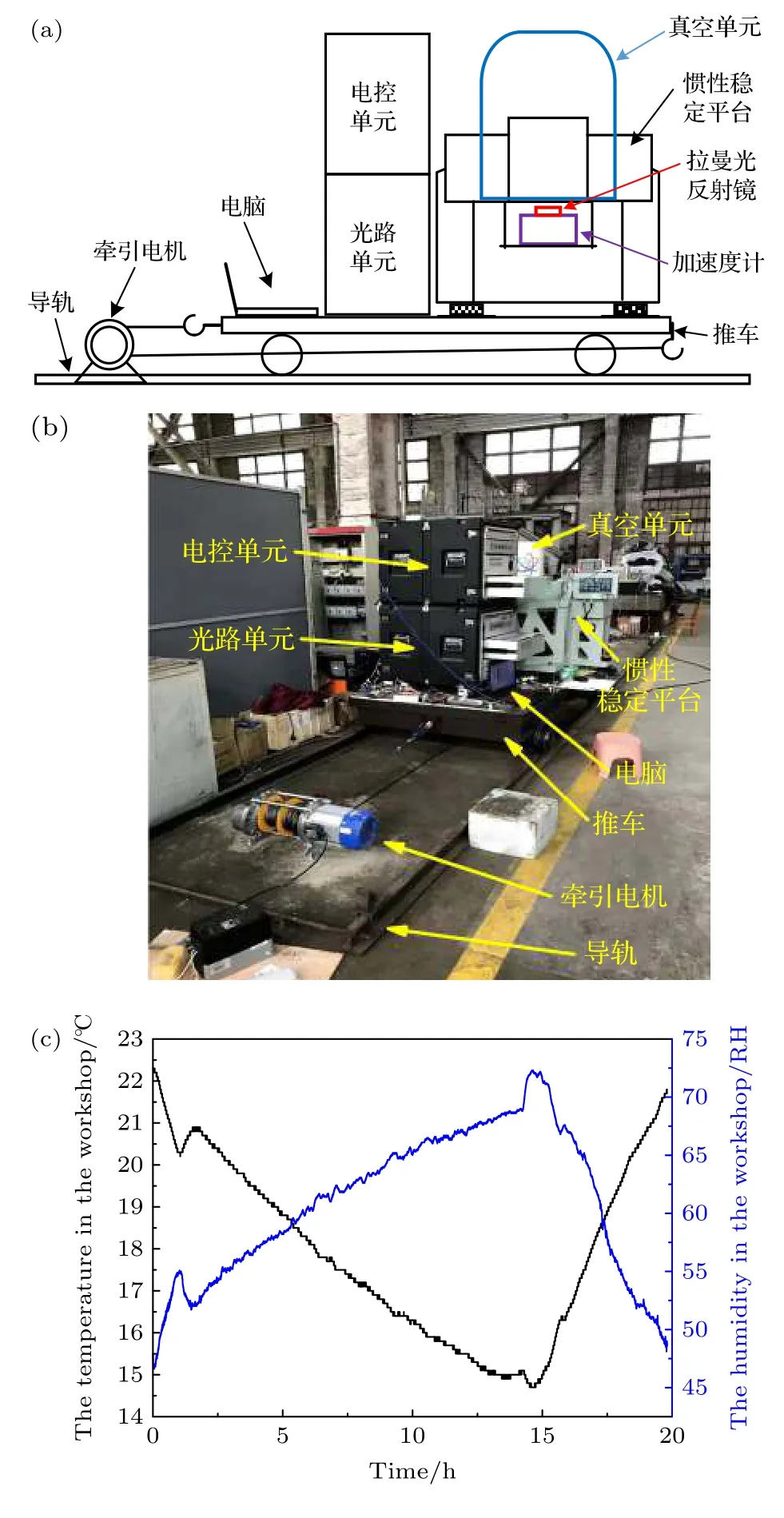
图3 绝对重力动态测量系统示意图和实物图 (a) 实验装置示意图;(b) 实验装置实物图;(c) 20 h中的温湿度统计曲线Fig.3.The diagram and photo of the system for dynamic measurement of the absolute gravity:(a) The diagram of the experimental system;(b) the photo of the experimental apparatus;(c) the curve of temperature and humidity in 20 h.

温湿度数据测量结果如图3(c)所示,温度变化范围为7.6 ℃,湿度变化范围为25%.温湿度的变化会影响原子重力仪测量系统中的光路单元,单元内激光的光功率、相位及偏振均会出现变化,但其变化趋势是缓慢的,对重力测量性能的影响是渐变的,随着时间累积会影响原子干涉条纹的对比度A和直流偏置B.温湿度波动引起的测量系统参数变化不可忽视,是影响测量性能的主要因素之一,但不能作为外部测量噪声进行滤波,因此在动态迭代条纹拟合算法中需要对参数进行预测.

3.2 实验步骤

在开展绝对重力动态测量之前,首先评估动态环境下的振动加速度噪声功率谱.系统预热后,惯性稳定平台和原子重力仪均进入工作状态,惯性稳定平台维持真空探头处于垂线状态.我们通过拉曼反射镜下的高精度加速度计记录不同牵引速度下的垂向振动信号,并基于原子干涉仪的灵敏度函数评估振动对绝对重力测量的影响.在此基础上,我们基于上述动态迭代条纹拟合算法研究振动补偿技术,通过记录不同牵引速度下的原子布居数分布和垂向加速度数据,利用动态迭代条纹拟合算法实时修正原子布居数的分布位置,恢复原子干涉条纹,通过正弦曲线拟合获取相位信息,从而计算出重力值.我们通过分析修正后的原子布居数分布情况,调整迭代算法中的参数取值,达到最佳的拟合效果.此外,为了开展绝对重力动态测量,我们分别配置了不同T的测量任务,并分析不同牵引速度对干涉条纹对比度、相位的影响,获取不同T下的重力值及其不确定度信息.最后,通过不同牵引速度计算科里奥利力效应对重力测量的影响,评估最终的绝对重力值.为了进一步验证重力测量的绝对精度,在静态环境下我们还测量了不同T下的原子干涉条纹,获得静态环境下的高精度绝对重力值,用于与动态环境下绝对重力测量值的比较.

4 实验结果分析

4.1 动态测量环境下垂向振动功率谱对重力测量的影响分析

由于测量点位于一个机械加工车间内,周围振动环境较为恶劣,在牵引电机关闭情况下先测量了地面垂向振动噪声.此外,为了开展动态测量实验,通过牵引电机设置了5种牵引速度,分别为0.55,1.35,2.25,3.75 cm/s和5.50 cm/s,在这5种牵引速度下分别测量了垂向振动噪声功率谱.测量数据如图4(a)所示,其中黑色曲线为推车静止时的垂向振动噪声功率谱,其他颜色曲线表示推车不同牵引速度下的垂向振动噪声功率谱,可以看出动态与静态环境下的振动差别较为明显.动态环境下,0.1—10 Hz频段垂向振动噪声显著增加(8 Hz处有一个共振峰),10—500 Hz频段垂向振动噪声也有所增加.随着牵引速度的增大,垂向振动噪声的幅度也相应增加,最大振动幅度可达0.1 m/s2.为了分析测量到的垂向振动噪声对原子重力仪性能的影响,结合原子干涉仪的灵敏度函数,得到了由垂向振动噪声引起的重力测量不确定度,结果如图4(b)所示.可知,在同一个T值下,随着牵引速度的增加,重力测量产生的不确定度将增大.当T=20 ms时,速度为5.50 cm/s引起的重力不确定度为4137.8 mGal,静止时的重力不确定度为62.7 mGal,两者相差65倍,且静止时的不确定度数值较大,我们无法得到准确的绝对重力值信息.可以看出,垂向振动引起的重力测量不确定度的变化是十分明显的,因此必须进行振动补偿.图中g0≈ 9793.4 mGal为实验室绝对重力参考值.

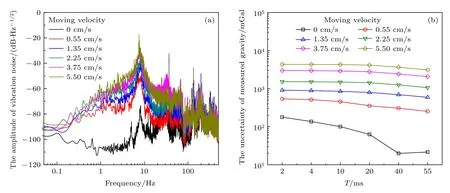
图4 垂向振动噪声对动态重力测量的影响 (a) 静止与运动状态下垂向振动加速度的噪声功率谱;(b) 垂向振动噪声引起的重力测量不确定度Fig.4.The influence of vertical vibration noise on the dynamic measurement of the absolute gravity:(a) The power density spectra of vertical vibration noise in the case of static and dynamic environment;(b) the measurement uncertainty resulted from the noise of vertical vibration.

4.2 动态测量环境下的振动补偿技术

4.2.1 动态测量环境下的原子干涉条纹恢复

在分析完振动噪声的影响之后,我们开展了动态测量环境下的振动补偿技术研究,以恢复原子干涉条纹.我们选择T=4 ms开展振动补偿实验,通过设置5种不同的牵引速度0.55,1.35,2.25,3.75 cm/s和5.50 cm/s,记录原始的原子布居数数据和干涉时间内的振动加速度信号;随后,通过计算振动加速度引起的相位 Δφvib,利用动态迭代条纹拟合算法更新了(4)式中的4个参数值,修正了原子布居数的分布位置,从而恢复出原子干涉条纹.不同牵引速度下恢复的原子干涉条纹如图5所示,其中黑色圆点是实测的原子布居数数据,红色圆点是修正后的原子布居数数据,紫色曲线是相应的拟合曲线.不同牵引速度下原子重力仪的扫频范围不变,图5(a)为静止时的原子干涉条纹,图5(b)—(f)为动态环境下的原子干涉条纹.由图可知,在0.55 cm/s牵引速度下通过原始数据仍然可以观察到原子干涉条纹,但是随着牵引速度增加,条纹变得越来越模糊和不可分辨.考虑到导轨的长度有限,牵引速度为5.50 cm/s时的原始数据的数量减少很多,垂向振动噪声也比较大,原子布居数分布呈现杂乱无规则分布(如图5(f)所示),但是经过振动补偿后仍能恢复出原子干涉条纹,这证实了振动补偿及动态迭代条纹拟合算法的有效性.

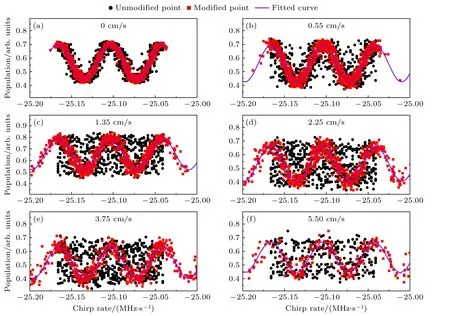
图5 不同牵引速度下的原子干涉条纹恢复及其正弦拟合结果(T=4 ms)Fig.5.The results of the recovering and fitting of the atomic interference fringes with the different moving speeds (T=4 ms).

4.2.2 动态环境下不同牵引速度对原子干涉条纹参数的影响分析

在上述恢复出的原子干涉条纹数据的基础上,我们进一步分析了不同牵引速度对原子干涉条纹各个参数的影响.由于机械加工车间的温湿度环境较差,且动态环境下的大振动会影响光路导致光功率变化,因此原子干涉条纹的对比度和直流偏置量将会发生变化,分析结果分别如图6(a),(b)所示.可知,原子干涉条纹的对比度在2.25 cm/s牵引速度后出现显著下降,下降幅度约为0.04 (相对变化约为15%).出现对比度下降的主要原因有三点.1)随着牵引速度增加,水平加速度也相应增加,下落的原子团在拉曼光场中的位置会发生变化,偏离中心,原子干涉的波前畸变比较严重,导致拉比频率不准,对比度会下降.2)冷却激光功率会出现波动,下落原子团的温度变高,导致参与干涉的原子数变少,导致对比度会下降.3)振动幅值越大,垂向方向的初速度越大,失谐量越大,此时原子团与拉曼光不严格共振,原子团与拉曼光之间的拉比频率改变,使得原子和拉曼光作用时的跃迁几率减小,从而引起原子干涉条纹对比度的下降.

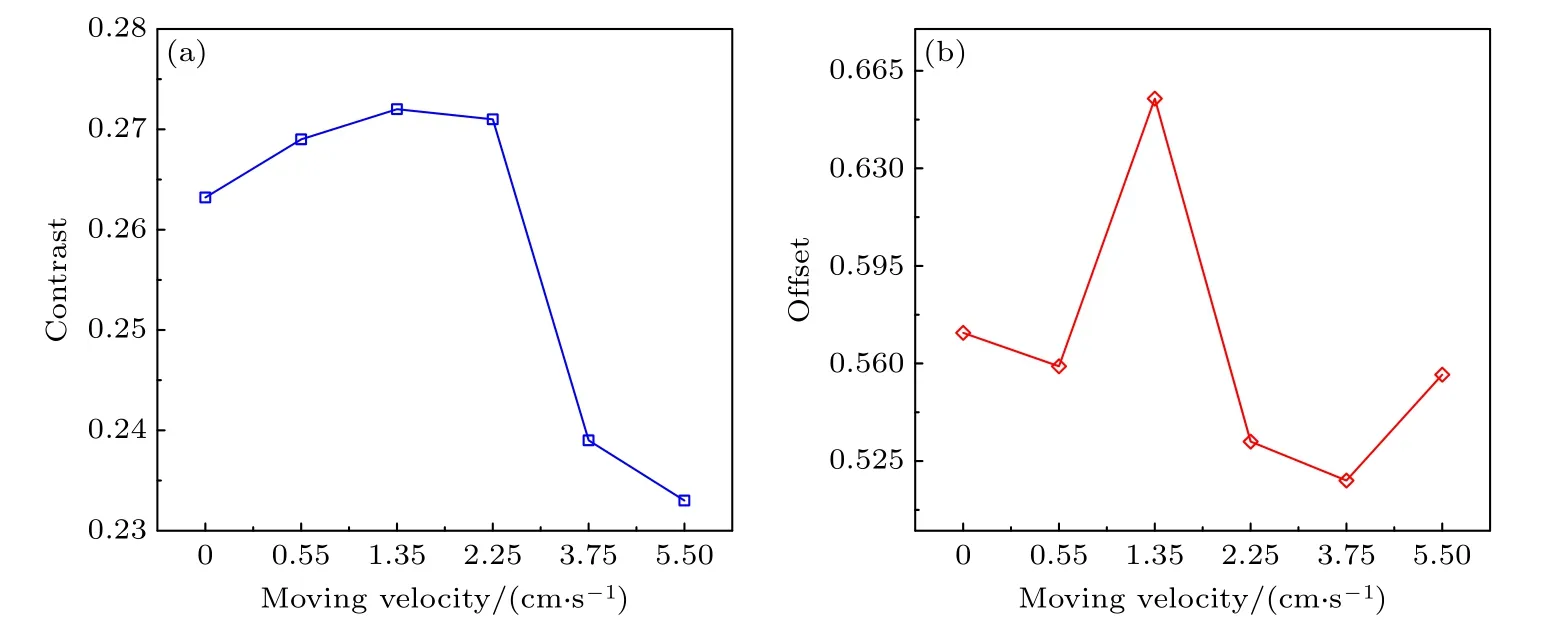
图6 动态测量环境下下原子干涉条纹对比度与直流偏置量变化 (a) 原子干涉条纹对比度随牵引速度的变化曲线;(b) 原子干涉条纹直流偏置量随牵引速度的变化曲线Fig.6.The changes of the contrast and offset of atomic interference fringes in the case of dynamic measurement environment:(a) The changing curve of the contrast of atomic interference fringes with the moving velocity;(b)the changing curve of the offset of atomic interference fringes with the moving velocity.

原子干涉条纹的偏置量约在0.525—0.665区间无规律变化,相对变化幅度约为23%.随着小车牵引速度的增加,虽然垂向振动的幅度变大,但从原子干涉条纹的参数变化上来仍然能够进行正弦拟合,可以有效提取重力加速度信息.

4.3 动态测量环境下的绝对重力测量

在验证了振动补偿技术的效果之后,进而开展动态测量环境下的绝对重力值评估工作.首先分析不同牵引速度对重力测量的影响,通过测量不同T值下的重力值以评估绝对重力测量值;其次,分析动态牵引速度引起的系统效应,评估出不同牵引速度下的科里奥利力效应修正值;最后,为了确认动态环境下测量的绝对重力值的准确性,我们开展了静态环境下的高精度绝对重力测量,比较了测量到的两个绝对重力值.

4.3.1 动态环境下不同牵引速度对重力测量的影响分析

在5种不同牵引速度下,我们分别设置T值为2,4,10和20 ms进行重力测量;通过振动补偿技术恢复出原子干涉条纹,拟合原子干涉条纹获取相位及其不确定度数据,进而获得重力值及其测量不确定数据,实验数据分别如图7(a),(b)所示.可知,随着T值增加,重力测量值的平均值逐渐趋于稳定,说明重力测量值不随T值发散,该点为暗条纹点,可以提取绝对重力值.同时,随着T值增加,原子重力仪的测量灵敏度提高,重力测量不确定度变小,在T值20 ms情况下,重力测量的标准差小于10 mGal.对比图4(b)中T=20 ms的重力测量不确定度曲线,经过算法补偿后的重力测量不确定度减小了很多,说明动态迭代条纹拟合算法是有效的.当速度为5.50 cm/s时,由于小车移动速度较快,垂向振动噪声较大,无法计算出有效数据,4.4节会分析原因.

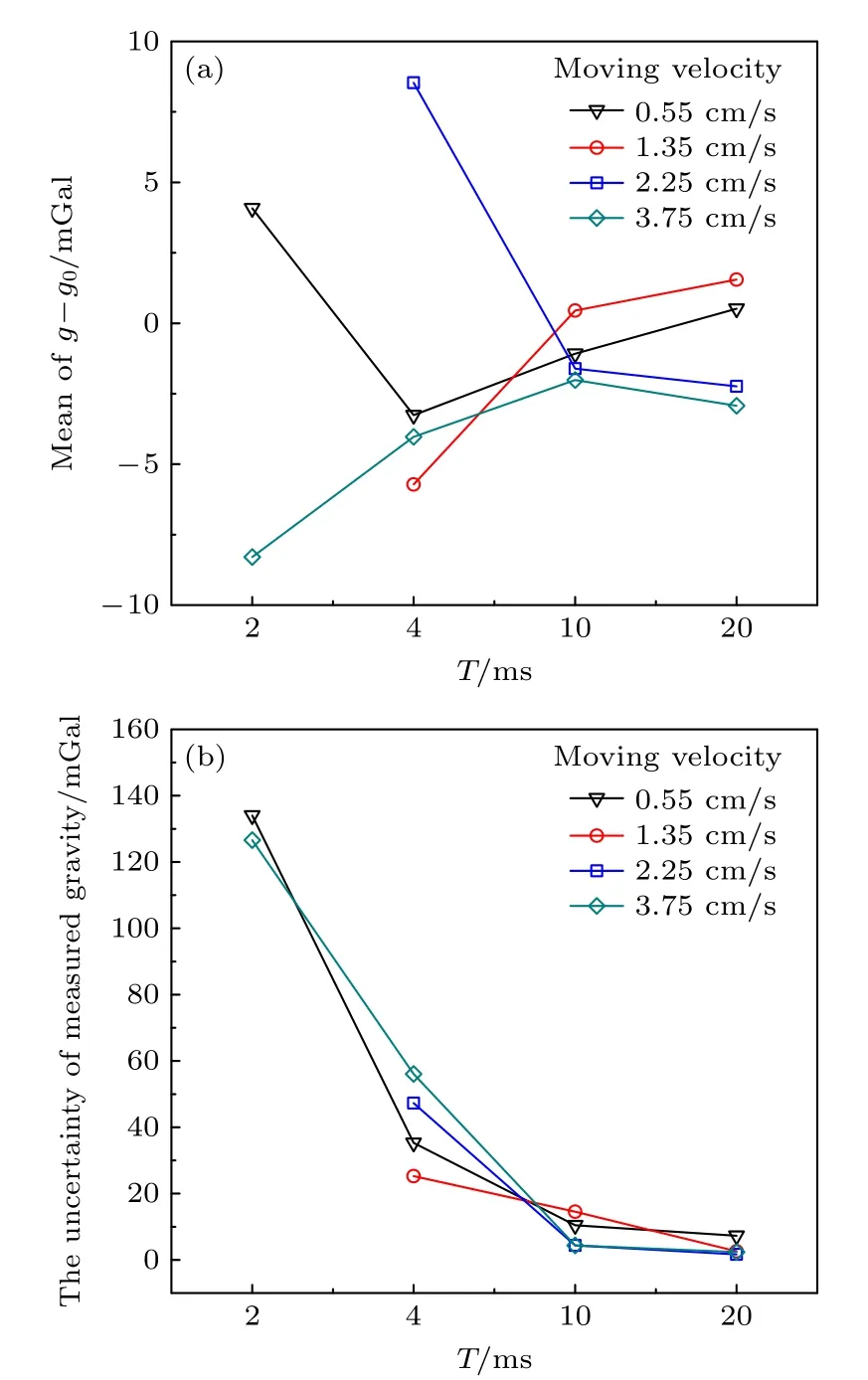
图7 不同牵引速度、不同T下测量到的绝对重力值均值及其不确定度分析 (a) 绝对重力值的均值数据;(b) 绝对重力值的不确定度数据Fig.7.Analysis of the mean values and uncertainties of the absolute gravity measurement at the different velocities and different T:(a) The data of mean value of the absolute gravity measurement;(b) the uncertainties of the absolute gravity measurement.

4.3.2 动态环境下科里奥利力效应的评估

动态环境不同牵引速度下,原子的水平初速度将发生一定变化,由科里奥利力效应引起的系统效应将会发生显著变化.考虑机械加工车间的纬度为30.31°,小车移动方向为北偏西5°,则由科里奥利力效应引起的重力偏置量可以通过下式计算:

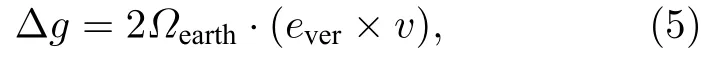
其中,Ωearth为地球自转角速度,v为原子在东西方向的初速度,ever为竖直方向的单位矢量.最终计算得到的科里奥利力修正值见表1.

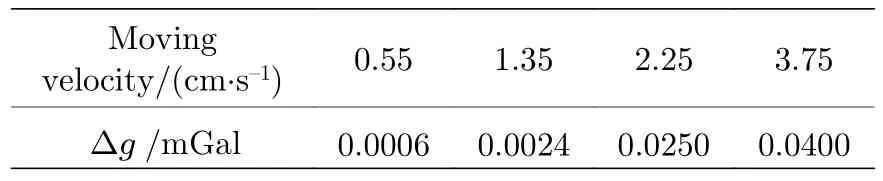
表1 由科里奥利力效应引起的重力值修正Table 1.The systematic corrections caused by the Coriolis effect.

修正完科里奥利力效应的最终结果(T=20 ms)如图8所示,重力测量值的平均值约为–1.22 mGal,平均值的标准差约为2.42 mGal.由图7可知,每一个牵引速度情况下基本能够通过动态条纹迭代拟合算法获得有效的绝对重力值,但是因为T值较小,每个点的测量不确定度都较大.所以本文选择3个不确定度较小的测量结果作为最终绝对重力动态移动测量实验的结果.

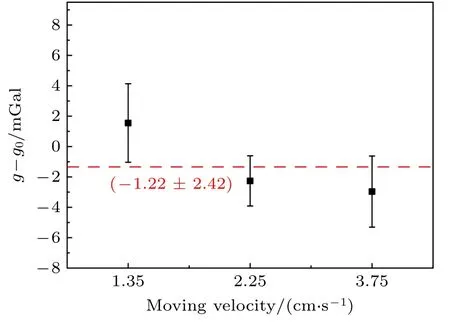
图8 修正完科里奥利效应后的动态绝对重力测量结果(T=20 ms)Fig.8.The final experimental results of the dynamic absolute gravity measurement after the correction of the Coriolis effect (T=20 ms).

4.3.3 动态环境下绝对重力值的确认

为了确认动态重力测量数据的精度,我们在小车上开展了静态高精度绝对重力测量实验.静态环境下,测量了T=2,4,10,20,40和55 ms的原子布居数分布及振动信号,每个T值测量10 min,同样利用动态迭代条纹拟合算方法计算重力值,结果如图9(a)所示.可知,T=2 ms时重力测量值变化的峰峰值可达125 mGal;随着T的增加,重力测量值的峰峰值变化越来越小,所有T值收敛到一个点,确定该点为绝对重力值点.为了方便评估,取T=55 ms长时间测量的重力值为绝对重力值,结果如图9(b)所示,减去实验室绝对重力参考值g0后约为(–2.29±0.05) mGal.

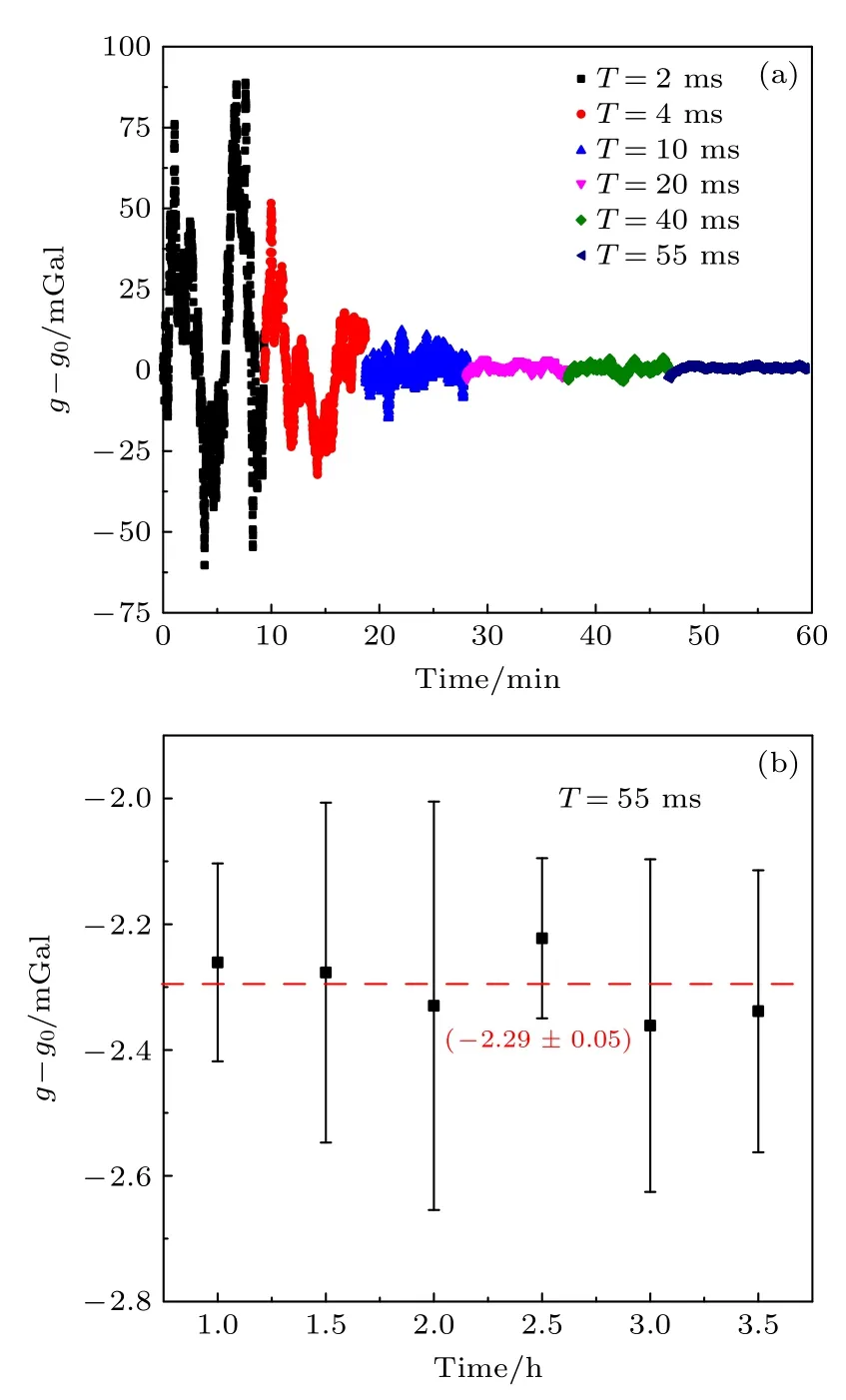
图9 静态环境下的高精度绝对重力值评估 (a) 静态下不同T的绝对重力测量结果;(b) T=55 ms长时间静态绝对重力测量结果Fig.9.The accurate evaluation of the absolute gravity in the case of static gravity measurement:(a) Absolute gravity measurements of different T at static state;(b) static absolute gravimetric measurements of T=55 ms for a long time.

车间静止环境下的重力测量不确定度高于实验室环境下的重力测量不确定度(0.01 mGal).经过比较,我们发现动态环境下和静态环境下分别测量的绝对重力值基本相吻合,约为(1.07±2.42) mGal.结果表明静态与动态均值相差1 mGal,不确定度主要源于动态测量的不确定度.我们会在4.4节中分析测量结果中存在测量偏差的原因.

4.4 问题分析与改进

4.4.1 问题分析

尽管实验数据验证了动态迭代条纹拟合算法的有效性,但是仍然存在诸多技术问题需要解决.当牵引速度为5.50 cm/s时,无法计算出重力值数据;动态环境下与静态环境下测量得到的绝对重力均值相差1 mGal;车间长时间静态测量与实验室静态测量的重力不确定度相差0.05 mGal;实验过程中无法开展更大T值的测量实验.下面我们对这些问题进行分析.

在小平台牵引速度增大后无法进行振动补偿,导致原子干涉条纹拟合失败,具体可能的原因如下:1) 加速度计的性能影响,测量过程中存在非线性环节和延迟,振动相位中仪器本身存在误差;2) 水平加速度串扰现象,加速度计的绝对水平姿态无法保证,且水平加速度数值较大,增加了振动测量误差;3) 惯性稳定平台的控制精度随着速度的增加而下降;4) 原子重力仪的光路单元受环境振动出现光功率、偏振波动的问题.

实验中动态环境下测量得到的绝对重力值存在多种不确定性因素,且静态与动态的系统效应也不相同,它们很难通过误差修正进行去除,因此测量结果相差1 mGal.具体原因分析如下.1) 静态与动态环境下的系统效应有所不同.动态测量时,GPS固定在户外,Coriolis相移评估不够准确;动态测量时原子团存在水平加速度,波前相移无法准确评估出来;动态测量时两束拉曼光的光移出现随机偏差,单光子光移无法有效评估.2) 动态环境下平台的垂向控制精度不同,动态环境下惯性稳定平台受到的外界干扰力矩会增大,平台控制的超调变大,调节时间变长,控制精度下降.3) 动态环境下拉曼光的重合度变差.动态测量时支撑拉曼光反射镜的框架会出现形变,反射镜会抖动,拉曼光的重合度出现偏差.4) 静态与动态环境下垂向振动信号的测量不同.加速度计在静止和动态环境下的测量性能存在差异,受带宽和动态性能影响,高频振动噪声会衰减,这部分的振动信息会丢失,最终的垂向振动相位出现偏差,这些问题可能会导致动态与静态环境下测量的绝对重力值均值不同.

本文实验中静态环境下的测量不确定度是50 µGal,大于实验室环境下的测量不确定度,主要原因是测量场地环境恶劣,影响了原子重力仪的性能.本文静态测量是在一个机械加工车间内开展,温度、湿度环境相对较差,导致激光功率、频率、相位变化较大,因此测量不确定度相比实验室恒温条件稍差.此外,本文实验中振动环境很差,绝对重力数据是通过基于加速度计的振动补偿获得,测量性能受加速速度计性能、振动补偿算法影响较大.

为了进一步分析车间静止环境下的不确定度,将原子重力仪的不确定度分为A类不确定度与B类不确定度,总的测量不确定度为两者的合成.A类不确定度主要体现为数据统计过程中产生的不确定度,形成的原因主要是设备本身的各个噪声源.将3.5 h的绝对重力测量数据进行分组求出相应的均值(表2),对所有均值求标准差即为A类不确定度,数值约为48 µGal.

表2 车间静止测量分组重力值Table 2.The measured gravity value in the quiet place of a workshop.

B类不确定度为除了统计以外的因素产生的不确定度,由原子重力仪的自身因素以及外界环境因素引起,表3罗列了主要的系统效应项目.

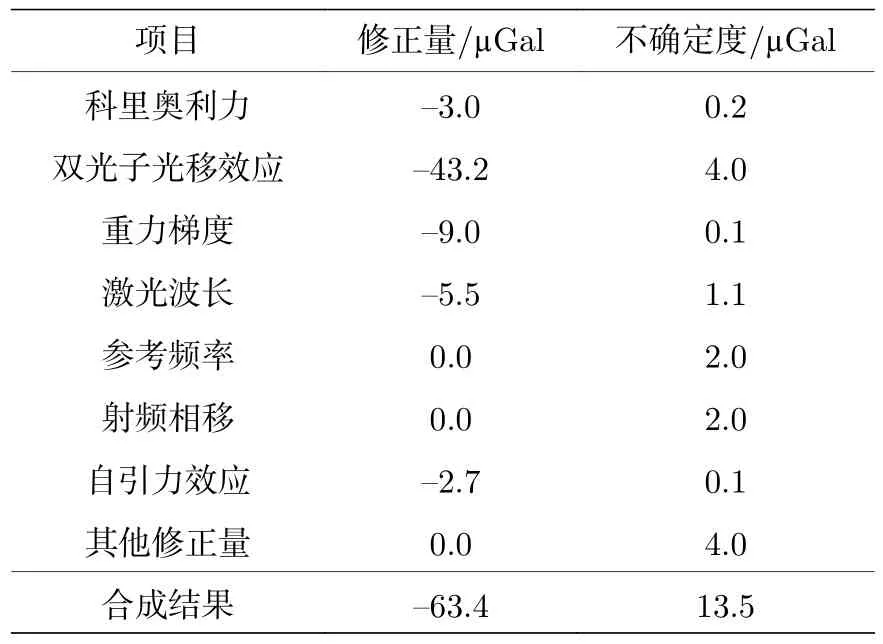
表3 车间静止下的B类不确定度表Table 3.The uncertainties of type B in case of static measurement in the workshop.

最终的合成不确定度数值为50.5 µGal,该评估结果与实际测量结果基本吻合.

实验中发现随着牵引速度增加,垂向振动噪声的幅度将变大,最大可达0.1 m/s2,该干扰加速度将远超过一条原子干涉条纹对应的加速度,导致无效的振动补偿.比如对于T=20 ms,单个原子干涉条纹周期对应的加速度范围一般在10–3m/s2,因此垂向干扰加速度会引起原子干涉条纹移动约100个条纹周期,考虑到目前加速度计的非线性、响应、噪声等,在强振环境下原子下落过程中包含了较多的振动测量误差,补偿后的布居数偏离真是位置,导致条纹拟合出现偏差.T值越大,原子干涉条纹的灵敏度和分辨率就越高,但计算得到的振动相位误差越大,导致无法拟合出条纹,这是本文实验中无法进行更大T的动态测量的原因.

4.4.2 系统改进方案

针对本次实验中存在的问题,系统设计方案需要进一步优化.首先需要筛选性能符合原子重力测量的加速度计,重点评估其闭环传递函数、系统灵敏度和系统带宽;为了减少振动带来的影响,测量系统中应增加减振装置,消除高频振动噪声,低频振动噪声使用振动补偿算法来进行补偿;由于水平串扰无法避免,所以必须要测量水平加速度,并结合惯性稳定平台的姿态角度进行校正;惯性稳定平台控制算法需要紧密结合原子干涉实验的特点,设计最优的控制算法.考虑到导轨的长度有限,牵引速度增加,测量的数据量也会变少,不便进行更大牵引速度下的测量,后续可以考虑增加导轨长度.此外,牵引电机的性能也有待改进,牵引速度可以更为稳定.最后,鉴于现有的动态迭代拟合算法中的4个参数调整采用最小二乘法,面对非线性环节时效果较差,因此需要设计自适应调节器来满足非线性要求.

5 结语

本文基于原子重力系统、惯性稳定平台系统和牵引动力系统搭建了一套绝对重力动态测量装置,并开展了绝对重力的动态测量实验.在先前振动补偿技术的基础上,完成了用于复杂动态环境的动态迭代条纹拟合算法的研究,改进了振动补偿的效果.同时,评估了不同牵引速度下的振动加速度噪声功率谱,发现垂向最大振动幅值可达0.1 m/s2;结合原子干涉仪的传递函数,理论分析了不同牵引速度下的垂向振动噪声对重力测量的影响.此外,基于不同牵引速度下T=4 ms的原子干涉信号以及加速度信号,验证了动态迭代条纹拟合算法的有效性.还分析了不同牵引速度对原子干涉条纹对比度和偏置量的影响,实验发现当牵引速度较大时,对比度会有0.04的下降,相对变化率可达14%,偏置量相对变化约为23%.在此基础上,测量了不同T值不同牵引速度下的原子干涉条纹,通过条纹收敛判断暗条纹位置,以提取绝对重力加速度值.为了得到更为准确的绝对重力值,基于牵引速度修正了由科里奥利效应引起的重力偏置量变化,最终得到在T=4 ms下不同速度的绝对重力值均值为–1.12 mGal,不确定度为2.42 mGal.最后为了进行验证,还进行了高精度绝对重力测量实验,发现静态与动态环境下测量得到的绝对重力值基本相吻合,约为(1.07±2.42) mGal.本次实验为绝对重力动态测量提供了验证,也存在一些技术问题需要解决,希望能为车载动态重力测量提供有价值的参考数据.