一种二级杠杆式声学释放器释放机构的设计与实现

陈凯云， 戈冬阁， 王士创， 张志平

(1.黑龙江科技大学， 哈尔滨 150022； 2.黑龙江科技大学 机械工程学院， 哈尔滨 150022)

0 引 言

海洋面积约占地球表面积的70%[1]，其中蕴含着丰富的自然资源。近年来，人类加大了对海洋的开发力度。声学释放器作为海洋观测中一种基础性设备，常用于海况恶劣、含沙量大、微生物浮粒多的海洋观测系统中。在海洋观测实验中，确保声学释放器高可靠性释放至关重要[2]。目前，国内外对声学释放器均有相关研究。J.C.Duinker[3]利用载人潜水器MIR1和MIR2对俄罗斯R/V Akademik Mstislv Keldysh号潜水器基本问题进行了研究，确定了海底系泊物的确切位置及其未能释放的原因。王欣[4]介绍了一种CTD电控多瓶采水器中电磁式释放机构，并进行了释放实验，验证了可行性。张学坪[5]采用故障树分析方法对QSF3-1型声学应答释放器进行了可靠性分析。常宗瑜等[6]采用多体动力学方法模拟声学释放器释放过程，有利于分析释放失效原因。在实用产品方面，美国Benthos公司、法国Ixblue公司、英国Sonardye公司[7]的产品可靠性高，我国国产释放器可靠性较低。目前，我国海洋工程、海洋救助和海洋打捞中使用的高性能深海声学释放器几乎全部依靠进口[8]。因此，研制具有自主知识产权的高可靠声学释放器至关重要。

文中设计了一种二级杠杆式声学释放器释放机构，理论计算了释放机构的强度可靠度，模拟仿真了释放机构的释放过程，分析了释放钩的运动情况，对释放机构进行了陆地释放动作实验。

1 释放机构设计

声学释放器处于整套海洋观测系统的下端位置。下端释放钩连接重物，起到锚定作用，上端有浮球组和其他相应的功能性组件，如沉积物捕捉器、温盐深仪和ADCP海流计等。如图1所示，到达观测年限后，水上甲板单元发出声学信号，释放器接收信息后驱动电机旋转，克服负载带动释放机构完成释放动作。

声学释放器在海水中的最大工作深度为11 000 m，承受海水最大压强约为110 MPa。同时，观测系统中重力锚负载与浮球拉力，最大约为10 t，需满足强度可靠性要求。TC4钛合金作为释放器主体材料，具有较好的刚度与耐腐蚀性。

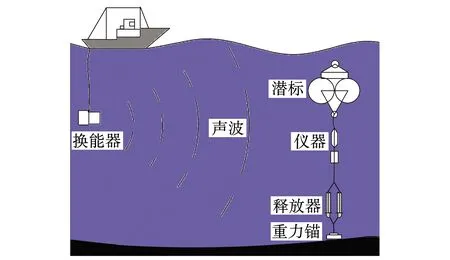
图1 释放器工作原理Fig. 1 Releaser working principle

如图2所示，耐压壳体与上下端盖形成密闭空间。耐压壳体采用圆筒形结构，受力均匀，避免应力集中。上下端盖处均由轴向密封和径向密封组成双重密封结构。传动轴处采用双重动密封，保证了密封的可靠性，保护内部电气结构。

释放机构作为声学释放器的重要组成部分，结构形式多样。文中释放机构采用二级杠杆式，具有较高的减力倍数，有利于负载释放，结构简单，易于制造，成本低。该机构包括齿轮组、二级杆螺栓、二级杆、侧板、释放钩(一级杆)、释放钩螺栓、旋转锁扣、二级杆销钉、旋转锁扣销钉等(如图2所示)。

驱动力由电机提供，选择直流减速电机，其转速慢、扭矩大，符合释放器使用需求。电机轴端通过键与小齿轮配合，经与小齿轮啮合的大齿轮传递动力给传动轴。传动轴上端与微动开关形成限位装置，确定复位原点，中段轴肩与止推滚针轴承配合进行轴向支撑，减小摩擦，下端与旋转锁扣连接。

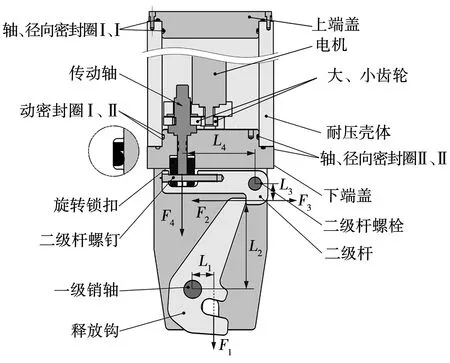
图2 二级杠杆式释放机构与受力分析Fig. 2 Two level lever release mechanism and force analysis

释放钩承受负载拉力，垂直向下载荷F1传递到二级杆；F2、F3分别为释放钩与二级杆之间的相互作用力，使二级杆产生逆时针旋转的趋势，旋转锁扣阻挡二级杆运动；F4为旋转锁扣作用在二级杆螺钉上的作用力。通过计算，选取合适的释放钩尺寸，既要满足强度需求，又要保证足够大的减力倍数。二级杠杆式释放机构与受力分析如图2所示。

由力矩平衡定理得：

F1L1=F2L2，

(1)

F3L3=F4L4，

(2)

F2=F3。

(3)

联立式(1)～(3)可得：

减力倍数：

释放器接收释放信息后电机转动，电机扭矩通过齿轮传递到传动轴，克服F4产生的摩擦力带动锁扣转动。当旋转锁扣转过45°时，二级杆在负载作用下从旋转锁扣中释放，完成释放动作。

2 可靠度的计算

2.1 构件的可靠度

释放器承受最大负载约为10 t，且受海流、波浪等载荷作用力，实际工况复杂，因此，需对其强度进行可靠性研究，以确保释放器各零部件强度可靠。文中采用一次二阶矩方法对释放机构的组成构件进行强度可靠度计算[9]，进而获得释放机构的总体可靠度。建立强度σs与应力σ表示的极限状态函数，即

g(σs,σ)=σs-σ，

式中:σs——材料的屈服强度，MPa；

σ——最大应力，MPa。

分析各零部件的受力形式。释放钩、二级杆以及旋转锁扣均为一端固定，另一端受到弯矩载荷的矩形截面悬臂梁结构。构件受力为所受负载F，负载与固定约束之间距离为l，最大应力为

式中:M——最大弯矩,N·mm；

b——矩形截面宽度,mm；

h——矩形截面高度,mm。

极限状态函数可表示为

符合悬臂梁模型的各零部件参数如表1所示，均服从正态分布。

表1 悬臂梁模型输入变量数值

释放钩螺栓、二级杆螺栓、旋转锁扣销钉以及二级杆螺钉，受力形式为两端固定约束，中间受集中载荷的圆形截面简支梁模型。构件所受负载F与固定约束之间的距离为l，横截面均为直径为d的圆形。最大应力为

极限状态函数可表示为

符合简支梁模型的各零部件参数如表2所示，均服从正态分布。

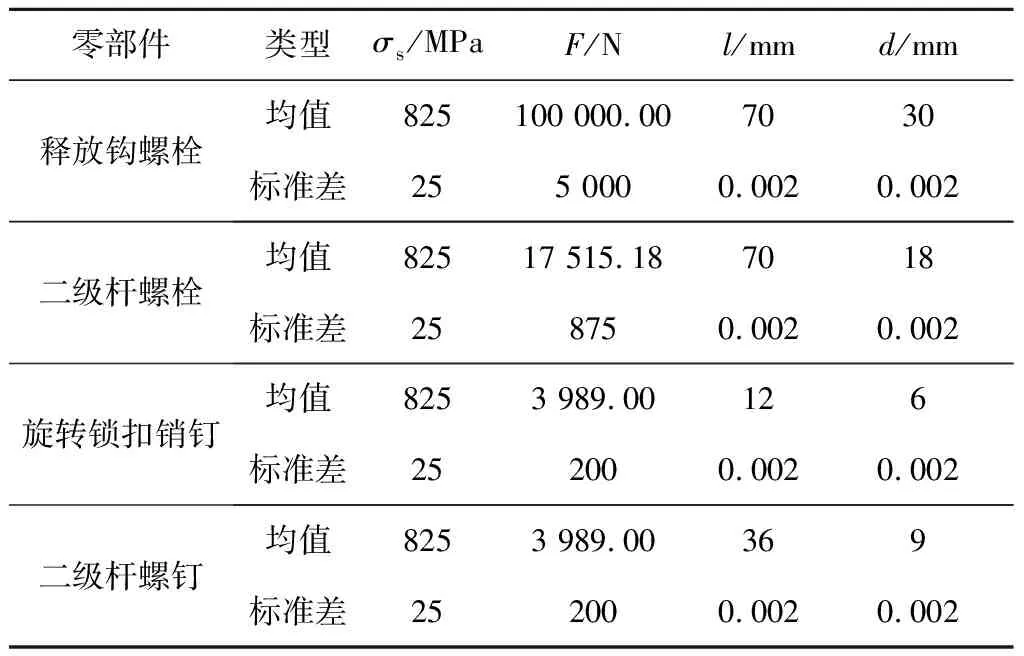
表2 简支梁模型输入变量数值

根据一次二阶矩法[10]计算得到各零部件结构的可靠指标为

全省国土资源工作会议暨党风廉政建设工作会议在杭州召开 （省厅办公室）..................................................1-4

实际工程中，σs、σ两个随机变量均服从正态分布[11],可靠度表达式为

根据实际工况和结构尺寸计算部件的可靠度。释放钩的可靠度Pr=0.999 998；二级杆的可靠度Pr=1；旋转锁扣的可靠度Pr=1；释放钩螺栓的可靠度Pr=0.999 5；二级杆螺栓的可靠度Pr=1；旋转锁扣销钉的可靠度Pr=1；二级杆螺钉的可靠度Pr=1。

2.2 释放机构的可靠度

释放机构各部件的可靠性模型为串联模型，其中任意构件发生失效都会导致释放动作失败。n个构件组成的系统的成功运行，必须满足所有的单元运行在正常状态，故系统串联模型的可靠度表示为

式中：xi——第i个单元处于运行状态；

Pr(xi)——第i个单元的可靠度。

则释放机构可靠度为各个构件可靠度之积，即

该释放机构的强度可靠度为99.949 8%。

3 释放动作仿真分析

3.1 仿真设置

释放机构传动失效亦会导致释放失败。仿真模拟释放动作，分析释放过程是否发生传动失效，影响释放动作，从而对释放机构能否正常释放进行验证。

将二级杠杆声学释放器释放机构的三维模型导入ADAMS软件中，设定构件运动副以及相互接触形式，给定减速电机转速，根据受力施加载荷，进行释放机构的释放动作仿真。仿真参数具体设置：释放钩承受的竖直向下的载荷10 t，所有部件相对运动摩擦因数为0.2[12]，减速电机转速为7.8 r/min。

3.2 仿真结果分析

从释放动作仿真得出：旋转销在电机的带动下缓慢旋转，当旋转锁扣转动45°时二级杆从旋转锁扣中顺利释放，如图3所示，释放钩在负载作用下顺时针转动，带动二级杆转动；当释放钩转过90°时，负载成功释放，释放钩在惯性作用下继续运动。

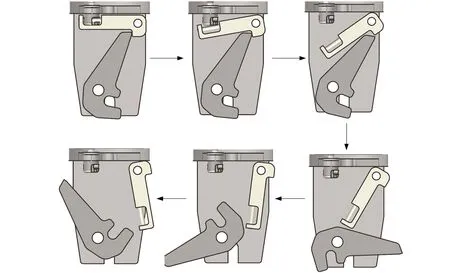
图3 释放机构释放状态Fig. 3 Release state of release mechanism

分析释放钩的接触面压力、角速度、角加速度的变化，可得出负载的释放变化状态。图4为释放钩压力p、角速度ω与角加速度α随时间的变化曲线。

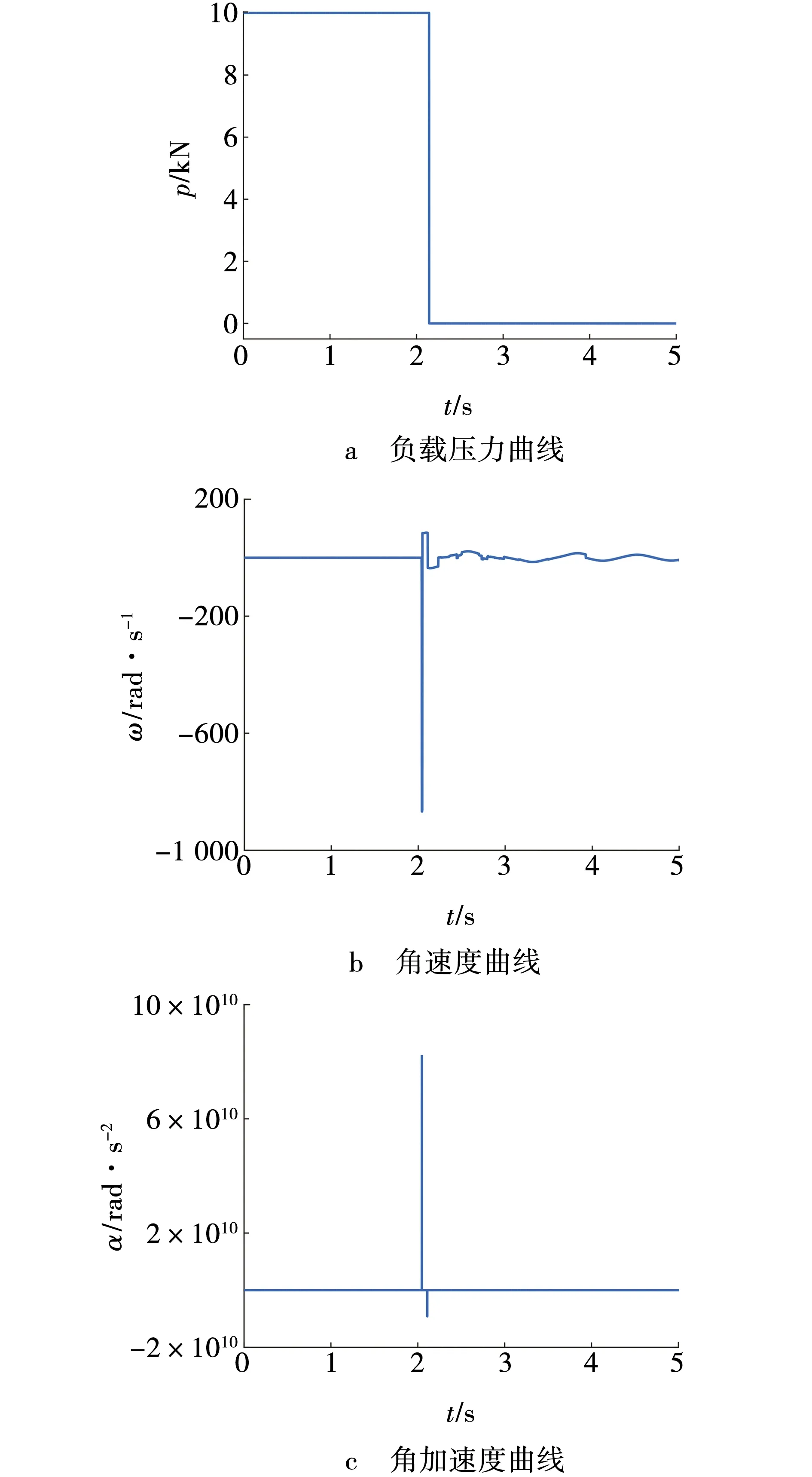
图4 释放钩释放状态Fig. 4 Release status of release hook

图4b显示，释放钩在2.025 s时发生转动，释放钩在负载作用下发生旋转，角速度与角加速度发生突变，负载得到释放，接触面压力减小为0。模拟发现，2.047与2.110 s时释放钩与二级杆发生两次碰撞，致使释放钩速度发生突变，速度方向改变，大部分动能被金属形变吸收，释放钩与二级杆速度都急剧减小，最终释放钩在阻力作用下摆动停止，整个释放动作结束。

由仿真知，在负载脱落释放钩释放过程中，虽然释放钩与二级杆发生两次碰撞(图3)，但是不影响释放动作，且会吸收释放钩大量动能，有利于释放钩快速进入稳定状态，加速释放进程，最终释放钩可靠地完成释放。

4 样机研制与实验

4.1 样机的研制

综合考虑各部件的位置关系、尺寸配合、强度可靠度和安全要求等因素，确定二级杠杆式释放机构样机，如图5所示。钛合金样机整体加工困难、成本高，故选用2205双相不锈钢作为替代材料。该材料具有耐腐蚀、强度高的特点。

图5 释放机构样机Fig. 5 Release mechanism prototype

释放机构二级杠杆减力倍数约为25.07，在10 t负载作用下，作用在旋转锁扣上的压力F4为3 989 N。传动轴与电机之间通过一对齿轮传动，齿轮组传动比为2.32，发挥放大电机扭矩、减小负载的作用。传动轴与电机轴并不同轴，避免了负载轴向力传递到电机轴造成电机损坏。

通过尺寸设计，使释放钩受力方向通过质心且与释放器轴线方向一致，保证了各部件受力均匀，工作时释放器姿态为竖直方向，有利于释放动作进行。

4.2 陆地负载释放实验

陆地释放动作实验模拟声学释放器受到系统拉力时的工作状况。施加10 t极限负载条件，检验释放机构能否正常传动、完成释放动作，并验证释放机构是否满足强度要求，从而检验声学释放器释放机构设计的合理性。为使二级杠杆式声学释放器释放机构能够安装在拉力机上，制做辅助夹具，如图6所示。

图6 释放机构辅助夹具Fig. 6 Release mechanism auxiliary fixture

将夹具安装到释放机构上，调整拉力机到合适位置，完成释放器装夹，启动拉力机对释放机构施予拉力，缓慢加载至10 t，保持一段时间，如图7所示。为减速电机供电(额定电压24 V)，电机转动约2 s后，释放钩打开，负载释放完毕，记录电机从开始转动到负载释放所用时间。

进行旋转锁扣与拉力机复位安装，再次进行试验，施加负载进行释放动作，重复10次，记录成功释放次数。

图7 声学释放器释放机构施加负载Fig. 7 Load applied by release mechanism of acoustic releaser

文中释放动作试验共进行10次，负载全部顺利释放。将实验完成后的释放机构取下测量，各构件未发生明显的形变，释放动作可靠度与部件强度可靠度高。

在释放过程中，从供电到负载释放所用平均时间为2.04 s，可以听到一声明显的金属撞击声，释放钩转动快速停止。根据仿真推论，释放钩与二级杆在极短的时间间隔内发生两次碰撞，声音重叠，人耳可听到有效撞击声为一次。通过陆地负载释放实验，验证了仿真结果的有效性，证明该二级杠杆式机械释放机构在10 t负载下能够可靠的完成释放动作。

5 结 论

对设计的二级杠杆式声学释放器释放机构进行受力分析，建立了系统可靠性模型。采用一次二阶矩方法对释放机构强度进行可靠度计算，释放机构整体可靠度为99.949 8%。使用ADAMS软件对释放机构释放动作进行仿真模拟，释放过程中释放钩与二级杆发生两次明显碰撞，负载顺利释放。根据设计结果研制样机，对样机释放机构进行陆地负载释放实验。通过拉力机对释放机构施加10 t载荷，在额定电压下，进行10次释放实验，负载均顺利释放，且释放机构未发生明显的形变现象。文中对声学释放器研制和失效原因分析具有借鉴价值与参考意义。

由于实验条件限制，未能进行真实海试实验。因此，与释放器真实工作环境相比，实验尚存缺陷，仅证明了在陆地释放的可靠性，未体现海洋环境对释放动作的影响。未来将进一步深化研究，验证提高释放机构的可靠性。