无锡硕放机场进近航空器复飞阶段碰撞风险评估

王勇 孙英然

摘 要：为评估无锡硕放机场雷达管制下进近航空器复飞阶段的碰撞风险，采用概率论模型，分别计算航空器侧向、纵向和垂直间的碰撞风险，从而确定总碰撞风险。经计算，无锡硕放机场进近雷达管制间隔18千米时以及缩小到10千米时，复飞阶段航空器的碰撞风险均满足安全目标水平。

关键词：碰撞风险;安全评估;复飞阶段

无锡地区经济发展迅速，促进了无锡硕放机场飞行量日益增加，自2020年12月31号无锡机场实施雷达管制至今，无锡机场雷达运行安全裕度较高、风险系数较低、目前的雷达间隔较大，为进一步增加空中流量，从航空器碰撞风险角度考虑，评估目前雷达管制间隔下进近航空器的碰撞风险，并尝试缩小间隔，以提高航空器在无锡硕放机场进近的运行效率。

在国外对航空器碰撞风险的研究，最早是英国的P.G.Reich提出一种碰撞风险模型，他分别从航空器的横向、纵向和垂直方向计算航路上的航空器间的碰撞风险，提供了一种确定航路间隔和评估航路系统安全等级的方法，为后续对航空器碰撞风险和间隔确定的研究奠定基础[13]。后来有学者开始研究航空器在进近过程中的碰撞风险，Domino D A等，通过实验模拟，分析了航空器进近時，采用驾驶员自主保持间隔的方法，航空器之间的碰撞风险[4];Madden M M通过研究航空器进近时，速度和位置的变化轨迹，对其进近过程中前后距离变化做了详细的分析，从而计算出碰撞风险[5];Guerreiro N等考虑了尾流的影响，分析其数据特征，建立了考虑尾流间隔的碰撞风险模型[6]。

在国内，张兆宁等在著作《飞行间隔安全评估引论》中，介绍了飞行间隔安全评估基本概念，并从安全目标水平的确定、RECIH改进模型及应用、基于时间的碰撞风险模型及应用、基于冲突区域和位置误差的概率模型及应用、最小安全间隔计算方法和基于CNS性能的安全评估模型，建立了飞行间隔安全评估理论体系[7];韩松臣等人考虑了在航路交叉点附近的航空器的标称位置的变化情况，认为在此处航空器的碰撞风险较大，所以引入时间间隔变量，计算了航空器在航路交叉点上的碰撞风险[8];卢飞等分别研究了航空器近距平行跑道配对进近时航空器间的纵向、侧向碰撞风险评估[910];张兆宁等人采用了基于事件概率思想建立碰撞风险模型，评估侧向跑道雷达间隔进场和离场时的碰撞风险[11];岳睿媛等提出使用改进的Event模型对航路上飞行的航空器垂直方向上的碰撞风险进行评估[12]。

对于无锡硕放机场进近航空器之间的碰撞风险评估，分为两个航空器同时进近时的碰撞风险、前机起飞后机进近时的碰撞风险和前机复飞后机进近时的碰撞风险。由于国内外针对航空器复飞阶段的碰撞风险评估研究不足，所以本文主要研究航空器在复飞阶段，即前机复飞、后机进近时的碰撞风险，为进一步缩小管制间隔提供依据。

1 航空器复飞阶段碰撞风险评估模型

1.1 航空器复飞阶段碰撞风险情况说明

在航空器进近过程中，如果无法保证安全着陆，就要执行复飞程序，当前机执行复飞程序时，与紧跟其后的正在进近的航空器之间存在碰撞风险。结合无锡硕放机场现状，可将复飞阶段的碰撞风险分为两种情况，如图1和图2。

图1中表示航空器A1使用03号跑道的进近程序进行进近，航空器B1使用03号跑道的复飞程序进行复飞，A1和B1之间存在碰撞风险;图2中表示航空器A2使用21号跑道的进近程序进行进近，航空器B2使用21号跑道的复飞程序进行复飞，A2和B2之间存在碰撞风险。

1.2 航空器碰撞风险模型

首先，计算两航空器纵向的碰撞风险，航空器i在t时刻纵向位置误差服从正态分布：

fix（t）～N（μix，σ2ix）（1）

设t时刻，航空器i距离基准航迹线上的基准点的纵向距离为dix（t），则此时航空器i的实际位置为：

Xi（t）=dix（t）+fix（t）（2）

由式（1）和式（2）得前后两架航空器在t时刻的实际纵向间隔为：

X1（t）X2（t）=（d1x（t）+f1x（t））-（d2x（t）+f2x（t））（3）

分解式（3）可得：

X1（t）X2（t）=（d1x（t）-（d2x（t））+（f1x（t）-f2x（t））（4）

其中令d1x（t）-d2x（t）=Lx（t），Lx（t）符合航空器进近时的运动学方程，且由式（1）得f1x（t）-f2x（t）～N（μ1xμ2x，σ21x+σ22x），则根据概率论计算两航空器t时刻纵向碰撞风险为：

PX（t）=12π（σ21x+σ22x）λxλxexp[（x（Lx（t）+μ1x-μ2x））22（σ21x+σ22x）]dx（5）

然后，同理得两航空器在侧向和垂直方向的碰撞风险为：

PY（t）=12π（σ21y+σ22y）λyλyexp[（x（Ly（t）+μ1y-μ2y））22（σ21y+σ22y）]dx（6）

PZ（t）=12π（σ21z+σ22z）λzλzexp[（x（Lz（t）+μ1z-μ2z））22（σ21z+σ22z）]dx（7）

最后，两航空器在t时刻，总碰撞风险概率为三个方向碰撞风险之积：

P=PX（t）×PY（t）×PZ（t）（8）

2 航空器碰撞风险评估参数

2.1 机型参数分析

根据航空器碰撞风险模型，计算碰撞风险时需要的机型参数是航空器的机身长λx、翼展λy和垂尾高λz。在计算时如果考虑飞机的具体机型，虽然符合实际情况，但是会增加模型的复杂程度，并且由于机场运行的飞机机型种类较多，考虑具体机型会导致计算量急剧增大，因此对机型做一般处理。考虑整体情况，将机型参数按照各机型的机队混合比进行加权平均，在计算过程中，所有的机型参数使用加权平均的结果。

设机型i的机队混合比为pi，机型参数为λi，j（j=x，y，z，x表示机身长，y表示翼展，z表示垂尾高），则机型几何参数可以表示为：

λi=∑iλi，jpi（9）

2.2 航空器位置误差参数分析

航空器位置误差表示为航空器偏离参考基准线的距离，对于采用标准进离场程序的航空器，参考基准线为相应的进离场程序，本文评估的是航空器复飞阶段的碰撞风险，所以仅考虑最后进近阶段，此阶段的参考基准线利用最后进近定位点即FAF点和跑道入口点的经纬度坐标计算，采用参数方程的形式给出。

设连接跑道入口点与FAF点的直线段方程如下：

y-y1x-x1=y1F-y1x1F-x1（10）

其中x1F

y1F表示直线段上给定点的纬度。化简为点斜式：

y=kx+b（11）

其中k=y1F-y1x1F-x1，b=y1-kx1。

给定航迹点P'=（x'，y'），假设直线段上离P'最近的点为P=（x，y），那么（x，y）可以根据如下公式进行计算：

x=x'+k（y'-b）k2+1

y=b+kx'+k2y'k2+1（12）

进而我们可以利用余弦定理计算P'到P的球面距离，也即P'的近似位置误差：

L=arccos（cos（90-y）cos（90-y'）+sin（90-y）sin（90-y'）cos（y-y'））180*π*R（13）

航空器運行过程中的位置误差分为纵向位置误差、侧向位置误差和垂直位置误差。

2.2.1 纵向位置误差

飞机在纵向的位置误差主要是由于飞机速度误差造成的，具体计算步骤如下：

Step1：计算n个航空器在进近阶段各自速度的平均值;

Step2：把平均值当作预设值，把航空器每个时刻的速度值与平均值的偏差视为速度误差;

Step3：计算进近时间段内以平均速度飞行的距离为均值μx，进近时间段乘以速度误差得到均方差σx。

2.2.2 侧向位置误差

飞机在侧向的位置误差主要受导航精度误差和飞行员操作误差影响，反映在三维空间，表现为航空器偏离基准航迹的水平距离，具体计算步骤如下：

Step1：根据进近程序和复飞程序，确定基准航迹线BaseLine;

Step2：描绘n架航空器在进近阶段的实际三维位置坐标（x，y，z）;

Step3：计算n架航空器进近时实际位置与基准航迹线的水平距离为均方差σy。

2.2.3 垂直位置误差

飞机在垂直的位置误差主要受气压高度修正误差、飞行员操作误差影响，反映在三维空间，表现为航空器位置偏离基准航迹的垂直距离具体计算步骤如下：

Step1：根据进近程序和复飞程序，确定基准航迹线BaseLine;

Step2：描绘n架航空器在进近阶段的实际三维位置坐标（x，y，z）;

Step3：计算n架航空器进近时实际位置与基准航迹线的垂直距离为均方差σz。

3 航空器复飞阶段碰撞风险评估结果

3.1 输入参数

根据无锡硕放机场2021年5月5日至2021年5月7日的航班运行数据，将机型参数按照各机型的机队混合比进行加权平均，得到中型机和重型机几何参数如表1所示。

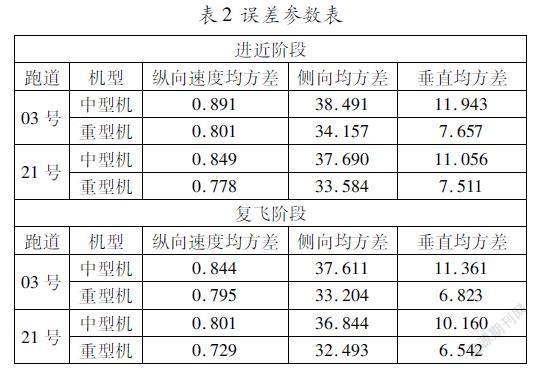
根据航空器位置误差参数计算方法，得到航空器在进近阶段和复飞阶段，分别在03号跑道和21号跑道的纵向速度均方差、侧向和垂直方向的位置误差均方差，如表2所示。

3.2 碰撞风险计算结果

将机型参数和航空器进近和复飞时的误差代入碰撞风险模型，计算当管制间隔分别为18千米和10千米时，使用03号跑道和21号跑道进近的航空器复飞阶段的碰撞风险如表3。

在管制间隔为18千米和10千米时，当前机处于复飞阶段、后机处于进近阶段的航空器碰撞风险满足1.0E7的安全目标水平。

结语

本文提出了航空器在复飞阶段的碰撞风险评估模型，对无锡硕放机场进近的航空器进行碰撞风险评估，当航空器进近时的雷达管制间隔为18千米时，碰撞风险值较低，安全裕度较高;当管制间隔缩小到10千米时风险值仍满足安全目标水平，故从复飞阶段的航空器碰撞风险角度考虑，可以缩小管制间隔，为实现缩小无锡硕放机场进近雷达管制间隔提供理论依据。

参考文献：

[1]Reich P G.Analysis of longrange air traffic systems：Separation standards I[J].Journal of Navigation，1996，19（1）：8889.

[2]Reich P G.Analysis of longrange air traffic systems：Separation standards II[J].Journal of Navigation，1996，19（2）：169186.

[3]Reich P G.Analysis of ;longrange air traffic systems：Separation standards III[J].Journal of Navigation，1996，19（3）：331347.

[4]Domino D A，Tuomey D，Mundra A，et al.Air ground collaboration through delegated separation：Results of simulations for arrivals to closely spaced parallel runways[C]//Integrated Communications，Navigation and Surveilance Conference（ICNS），2011.

[5]Madden M M.Kinematic Modeling of Separation Compression for Paired Approaches to CloselySpaced Parallel Runways[C]//Aiaa Aviation Technology，Integration，& Operations Conference，2006.

[6]Guerreiro N，Neitzke K.Simulated Wake Characteristics Data for Closely Spaced Parallel Runway Operations Analysis[C]//Aiaa Aviation Technology，Integration，& Operations，2013.

[7]張兆宁，王莉莉，李冬宾.飞行间隔安全评估引论[M].科学出版社，2009.

[8]韩松臣，曲玉玲，孙樊荣，朱新平.航路交叉点处碰撞风险模型[J].西南交通大学学报，2013，48（02）：383389.

[9]卢飞，张兆宁，魏志强，刘碧莲.近距平行跑道配对进近纵向碰撞风险安全评估[J].中国安全科学学报，2013，23（08）：108113.

[10]卢飞，朱楠，杨斯，张兆宁，刘碧莲.近距平行跑道配对进近侧向碰撞风险评估[J].中国安全科学学报，2016，26（11）：8792.

[11]张兆宁，徐超，卢婷婷.雷达间隔下的侧向跑道运行碰撞风险[J].科学技术与工程，2019，19（25）：386391.

[12]岳睿媛，苏彬，朱新平，曹哲.基于改进Event模型的航路飞行过程垂直碰撞风险研究[J/OL].航空工程进展，20210816：16.

基金项目：中央高校基本科研业务费中国民航大学专项（3122017061）资助

作者简介：王勇（1971— ），男，江苏东海人，高级工程师，现为苏南硕放国际机场有限公司航行保障部经理（兼书记）;孙英然（1997— ），女，河北承德人，硕士，研究方向：空中交通运输规划与管理。