武夷山地区短时冻期边坡浅层温湿度变化的数值模拟

袁文豪，王荣，林伟

（1.福建船政交通职业学院 土木工程学院，福建 福州 350007；2.武夷学院 土木工程与建筑学院，福建 南平 354300；3.福州大学 土木工程学院，福建 福州 350116）

福建省位于我国东南沿海，境内短时冻土（土体冻结时间在几小时至几天）主要分布在闽西北，面积约2 万km2。福建短时冻土区既有土坡广泛在每年降雨量很少的冬季出现浅层失稳现象，但破坏原因存在困惑。现场调查表明，短时冻区所引发的土坡浅层短时反复冻融是影响该区域内土质边坡冬季失稳的重要原因。因此，研究短时冻区气候下的土坡浅层温湿变化具有重要意义。与此同时，国内外学者针对多年与季节冻土工程的水热力耦合进行大量研究，取得许多重要的成果[1-3]。然而上述研究对短时冻区土质边坡水热变化研究还较少。事实上，南方短时冻土与多年、季节冻土相比，其冻结深度、冻结及热融过程均不尽相同[4-5]。基于此，依据武夷山地区冬季典型短时冻融气候，采用有限差分原理编制冻土水热耦合程序，模拟武夷山地区典型短时冻融气候条件下边坡浅层温湿度场变化规律。通过研究，可以掌握武夷山地区典型气候下温度场和水分场的变化规律，为下一步边坡力学场的分析提供重要依据，从而为武夷山地区典型气候条件下边坡工程的设计、施工提供借鉴指导。

1 冻土水热耦合模型与求解

1.1 水热耦合方程与程序编制

冻融条件下，水热耦合运移问题必须联立求解土壤水分运动和热流两个基本方程[2]，其中水分运动方程主要基于质量守恒定律和非饱和达西定律而来，对于水热耦合问题，水分运动方程中多了一项 “含冰率”；温度方程基于能量守恒定律和Fourier 热传导理论而来。只考虑土壤中的水热场，忽略应力场和溶质场，且短时冻土地区气态水和温度梯度的影响较小，基于Harlan 模型可得非饱和冻融条件下土壤水热一维耦合模型为:

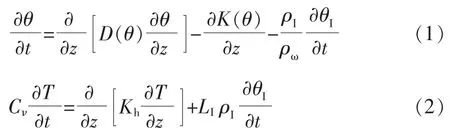
式中:θ、θI分别为含水率和含冰率；D（θ）、K（θ）分别为非饱和土水分扩散率和导水系数；T、t 分别为温度及时间；Cν为土壤体积比热容；Kh为热导率；LI为冰的融解潜热，一般近似取335 J/g；ρω、ρI分别为水和冰的密度，两者依次取值1 g/cm3和0.917 g/cm3。

基于交替隐式差分（ADI）方法对式（1）、式（2）进行求解，采用MATLAB 语言编制程序。

1.2 参数取值

方程（1）中的导水系数K(θ)通过VG 模型求解，即通过已知的饱和导水率求得土体非饱和导水率[6]，方程如下:

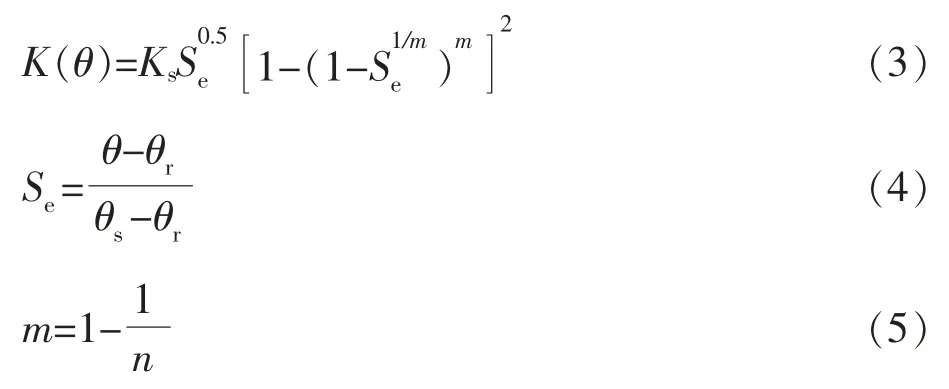
式中:Ks为饱和导水率；Se为有效饱和度；θr和θs分别为残余含水率和饱和含水率，n 为土水特征曲线参数。

选取武夷山地区典型土质，按《公路工程试验规程》 试验采用变水头试验测得残积土饱和导水率，土水特征曲线参数通过定量滤纸法并利用Matlab 中的Isqcurvefit 函数拟合得出，具体参数如表1 所示。

表1 水分运动方程参数取值Table 1 The parameters of the water movement equation are taken℃

非饱和土水分扩散率由以下经验公式给出[5，7]:

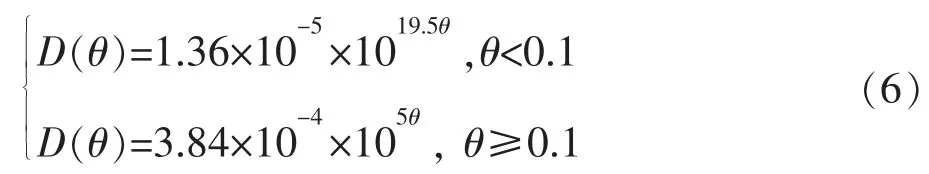
方程（2）中土壤体积比热容Cv按冻融土各成分质量加权平均求得，主要考虑组成成分为土骨架、水和冰，各类土骨架比热容参考值参考文献[8]，根据室内试验测得的残积土土骨架类型可得土骨架比热容，然后根据水和冰已知的比热容可得土壤体积比热容Cv=1 196 J/(cm3·℃)。

热导率Kh参考文献[9]中的公式，并根据室内土工试验测得的干密度求得，其值为5 568 J/(cm·℃·s)，未冻含水率与负温关系按下列经验公式给出:

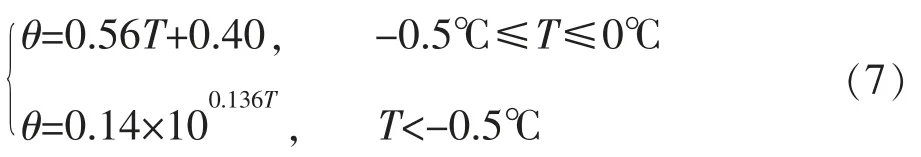
1.3 边界与初始条件

初始条件:温度T（t=0，z）=5℃，总含水率ω（t=0，z）=0.20，未冻含水率ωl（t=0，z）=0.20，含冰率ωI（t=0，z）=0。

选取武夷山地区2009 年1 月10 日至2009 年1月16 日共7 d 的短时冻融气象数据（如表2 所示），计算模型假定深度为2 m，且地下水埋深大，毛细水无法为冻结区补给水量。坐标系取地表为原点，向下为正。

表2 2009 年1 月10 日—2009 年1 月16 日武夷山地区气温资料Table 2 Temperature data for the Wuyishan region from January 10,2009 to January 16,2009

1.4 模型验证

为验证上述计算模型的准确性，选取武夷山地区境内省道303 线K 364+900 处边坡作为本次试验的监测点，该地区具有典型的南方短时冻土的气候特点。监测该地区土壤层内固定位置温度和体积含水率的变化规律，并与数值模拟结果对比。监测仪器采用PC-3 型移动式自动气象站，该仪器可监测环境的温湿度。监测时间为2008 年12 月27 日，测点1 和测点2 深度分别为12 和27 cm。2 个测点的温度和体积含水率监测值和模拟值分别如图1 和如图2 所示。

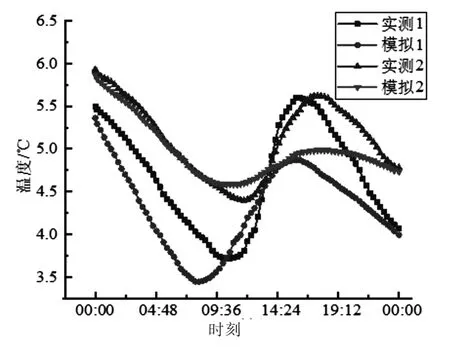
图1 监测点温度对比Fig.1 Temperature contrast of monitoring point

图2 监测点体积含水率对比Fig.2 Comparison of volumetric moisture content at monitoring points

由图1 所示，2 个监测点温度的检测值和模拟值变化趋势相同，虽然存在一定误差，但是误差总体上均小于1 ℃，产生误差的可能原因有如下:一是数值计算有限差分节点温度在0 ℃至冻结温度范围，未考虑土壤参数的变化；二是MATLAB 有限差分计算采用方块几何模型计算，而实际情况则为边坡模型，边界条件按坡度做出折算后再代入模型，两者存在一定偏差；三是由于操作误差，现场监测点的埋设尺寸存在一定偏差。由图2 所示，2 个监测点体积含水率的实测值与模拟值基本相同，其日变化范围大致在0.001～0.002，主要原因是受到蒸发的影响。综上，虽然数值计算结果与实测值存在一定偏差，但该偏差在可控范围之内，因此，可采用本数值模型计算短时冻土边坡温湿度。

2 短时冻土边坡水热耦合模拟结果与分析

2.1 边坡温度变化

基于2009 年1 月10 日至2009 年1 月16 日共7 d的短时冻融气候条件，通过数值模拟得到7 d 的边坡温度总变化如图3 所示。由图可见，边坡浅层温度状况随气温的变化基本呈周期性的变化规律，且存在边坡浅层温度滞后气温的现象。同时，边坡浅层（0～15 cm）最低温度在每天均达到零下，最大值约-5.1 ℃；而最高温度可达13.5 ℃左右。

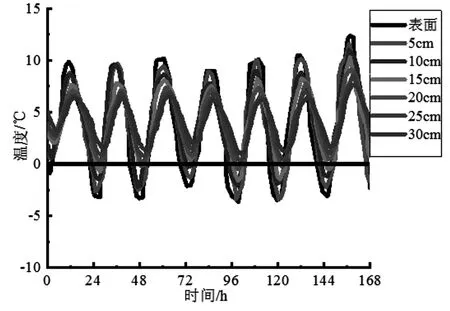
图3 2009 年1 月10 日—2009 年1 月16 日不同深度边坡温度变化Fig.3 Slope temperature changes at different depths from January 10,2009 to January 16,2009

以2009 年1 月11 日为例，边坡不同深度和不同时刻处温度计算结果如图4 所示。

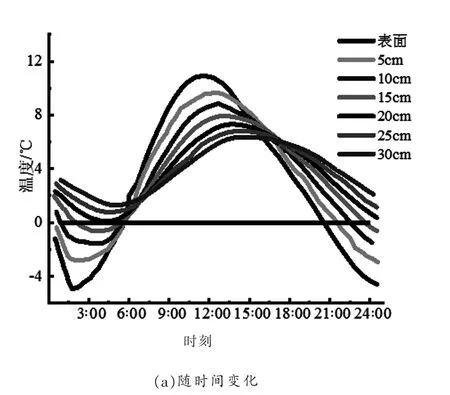
从图4 中可以看出:

（1）表层土体从夜间21:00 到次日凌晨5:00 之间，土体温度低于0 ℃。地表温度刚开始下降时，地表浅层降温迅速，5 cm 处2 h 之内温度大约降低3 ℃，但由于低温天气持续时间有限，而气温对土体的影响存在一定滞后性，故影响深度十分有限。

（2）未冻土段斜率明显大于冻土段，说明未冻土段的温度梯度小于冻土段。随着持续冻结，未冻土段和冻结段的斜率都在提高，说明随着时间的增加，冻土层和未冻土层温度梯度逐渐减小，温差变小。原因在于在冻结之初由于地层表面为负温，而土层内部为正温，存在较大的温差，所以冻土层的温度梯度较大；然而随着时间的增加，地层间的温差渐渐减小，温度梯度变小。

（3）从0 点至次日0 点，表面土体温度约8 h 处于0 ℃以下，最低温度达-5 ℃，5 cm 处土体约7 h 的时间处于0 ℃以下，但最低温度只有-3 ℃，而10 cm处土体约有5 h 的时间处于0 ℃以下，最低温度高于-2 ℃，15 cm 处土体位于0 ℃以下时间小于3 h，20 cm 深度处土体温度高于0 ℃。鉴于土体冻结温度通常低于0 ℃，因此，判断冻土影响深度为10 cm 左右。

2.2 边坡水分变化

图5～图10 为在7 d 的冻融过程中，土体在不同时刻不同深度总含水率、未冻含水率和含冰率的变化曲线图。

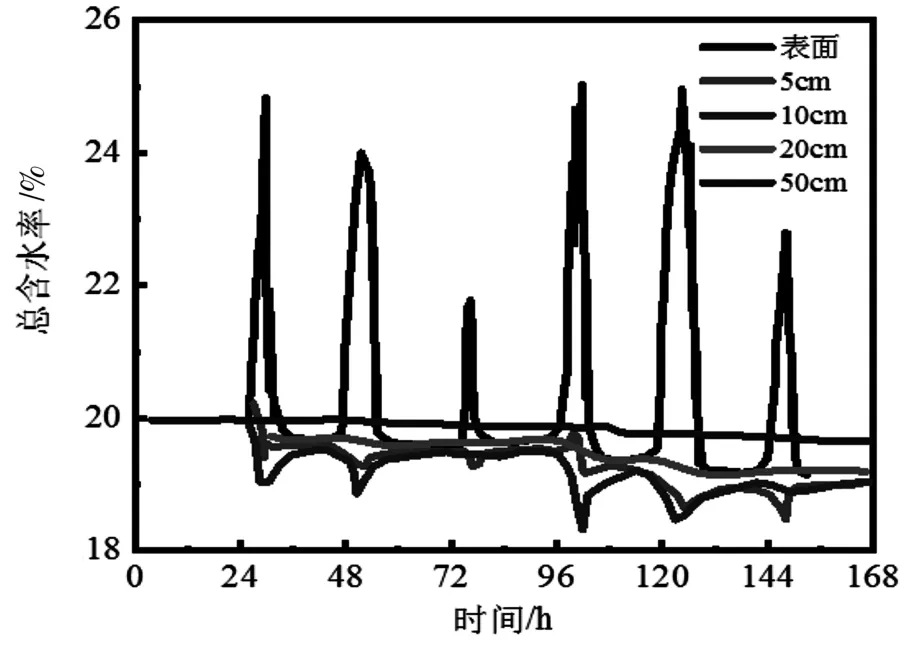
图5 2009 年1 月10 日—2009 年1 月16 日不同深度边坡总含水率变化Fig.5 The change of total moisture content of slope in different depth from October 10,2009 to January 16,2009

从图5 和图6 可见，经过一定的冻结时间后，上部土层的总体积含水率增大，中间层位土体总体积含水率略有减少，而下部土体总体积含水率基本不变。如经过约3 h 的冻结，地表的含水率由初始的20%提升到25%，地层在0～5 cm 厚度范围内含水量提高明显，5 至20 cm 深度范围内总含水量降低，而在20 cm深地层以后总含水量基本没有变化。这是因为随着冰冻，地层内毛细水持续不断向冻结层移动，而冰冻层内毛细水或间隙水则移向地表，导致地表含水量显著提高，而冰冻层以下土层的间隙水或毛细水移出后，没有及时补给，造成含水率降低。

图6 2009 年1 月11 日边坡水分变化Fig.6 Moisture change of slope in January 11,2009

从图7 和图8 可见，随着冰冻的持续，地表以下15～20 cm 深范围内的未冻地层含水率逐渐降低，其含水率由未冻前的20%降低至16%左右，土层孔隙则由冰填充。但随着冻结土体的融化，土体未冻含水率大幅度上升，这是因为表土总含水率在冻结过程中不断上升，此时冻结的土全部融化，从而导致未冻含水率大大上升，如地表处未冻含水率由冻结时的16%大幅度上升至后来的25%，基本趋于饱和状态。随后由于重力势的作用，水分向下迁移，未冻含水率恢复至正常水平。

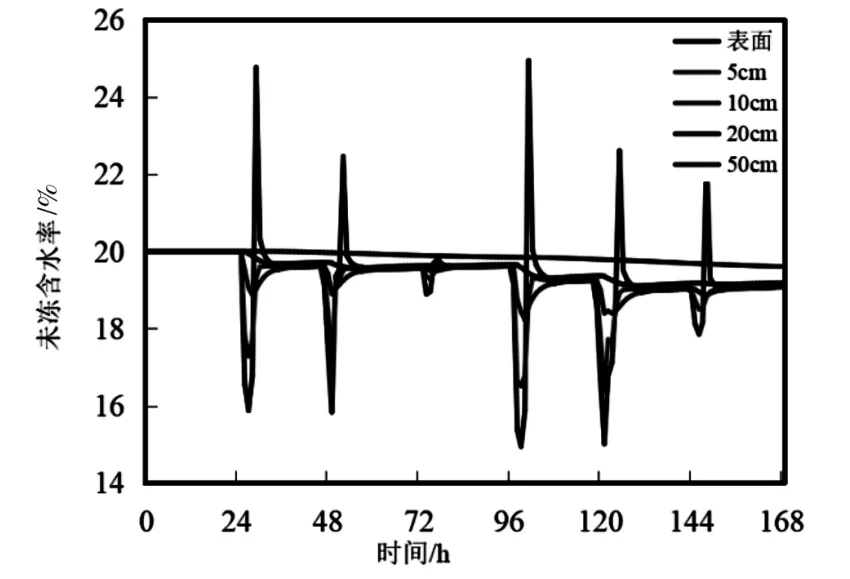
图7 2009 年1 月10 日—2009 年1 月16 日边坡未冻含水率变化Fig.7 The change of unfrozen moisture content of slope from October 10,2009 to January 16,2009

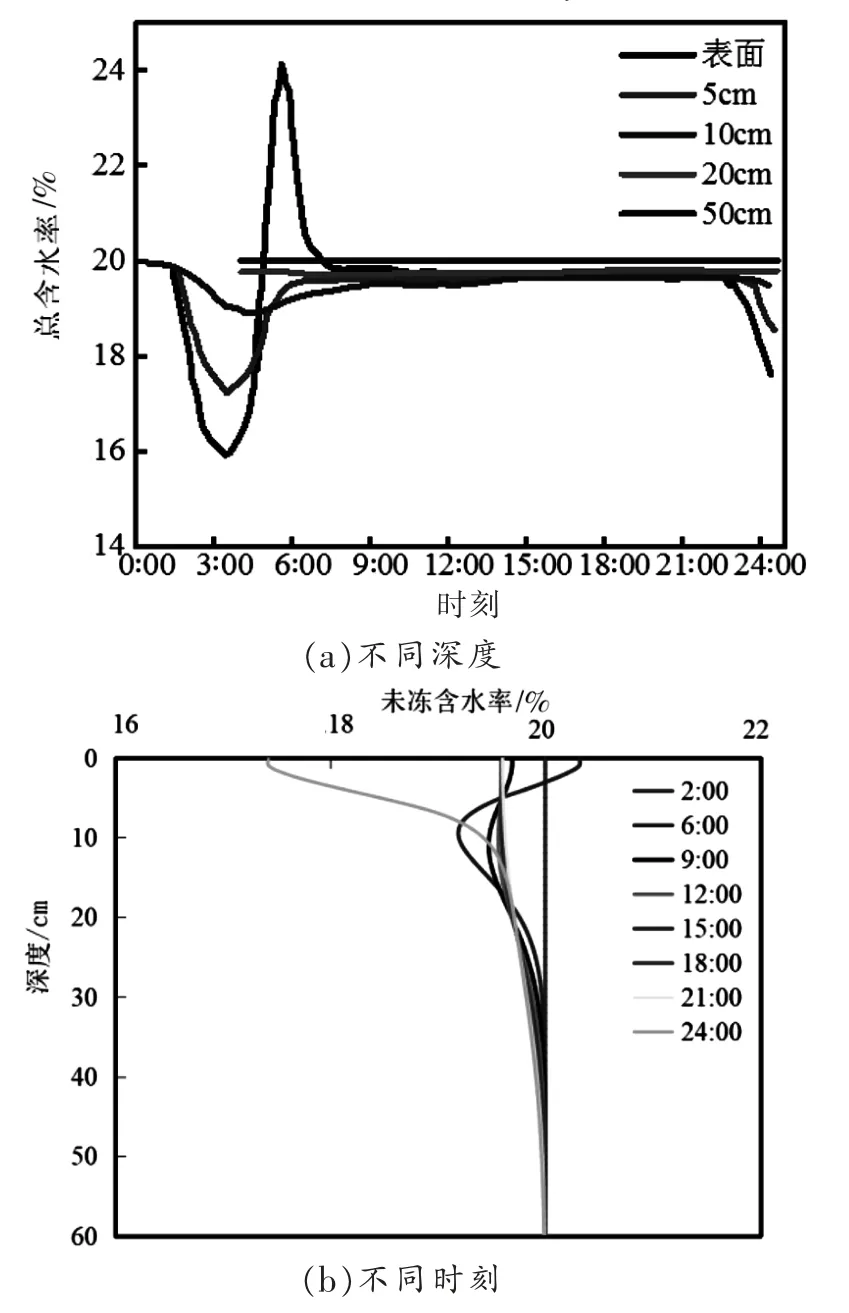
图8 2009 年1 月11 日不同深度不同时刻边坡未冻含水率变化Fig.8 Change of unfrozen moisture content of slope at different depth and time in January 11,2009

从图9 和图10 中可见，土体含冰率主要出现在浅层土体约10 cm 深度范围内，即武夷山地区土体冻结深度约为10 cm，其中，表土含冰率最高可达8%，随着深度增加，含冰率显著减小。

图9 2009 年1 月10 日—2009 年1 月16 日不同深度边坡含冰率变化Fig.9 The change of ice content in slopes with different depths from October 10,2009 to January 16,2009

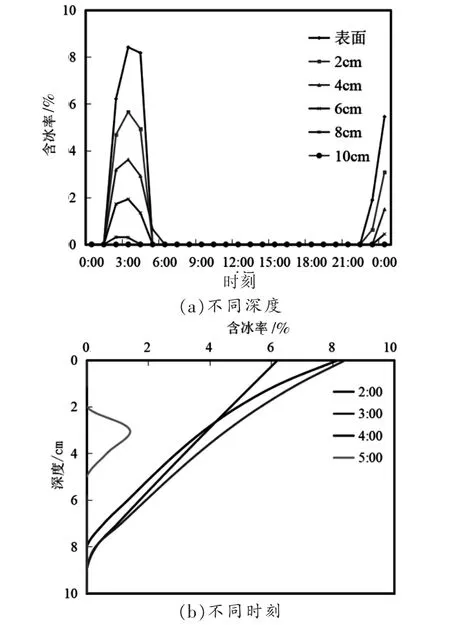
图10 2009 年1 月11 日不同深度不同时刻边坡含冰率变化Fig.10 Changes of ice content in slope at different depth and time in January 11,2009

综上可以得知: 无论是未冻层含水量，还是总含水率，地表浅层的间隙水或毛细水含量变化都最显著，而距地表10 cm 深度以下地层总含水率和未冻水含量基本未发生较大变化。这说明冻结层水分迁移现象最明显，水分聚集最严重，武夷山地区冻结层厚度约为10 cm。

3 结论

运用冻融状态下的温湿耦合模型，以武夷山地区的气候条件为背景，对该地区边坡浅层温度和湿度变化进行研究，得出福建省北部典型短时冻土区边坡温度场和湿度场变化规律，结论如下:

（1）边坡浅层温度状况随气温的变化基本呈周期性的变化规律，且存在边坡浅层温度滞后气温的现象。同时，边坡浅层（0～15 cm）最低温度在每天均达到零下，最大值约-5.1 ℃；而最高温度可达13.5 ℃左右，表层土体冻结时间在夜间21:00 到次日凌晨5:00 之间。

（2）冰冻之初，未冻土层的温度梯度小于冻土层，而随着冰冻的持续，冻土层和未冻土层内温度梯度降低，温差逐渐变小。

（3）不论是总含水率，还是未冻水含量，地表浅层的含水率变化幅度都最大，而10 cm 以下的含水率曲线平缓，总含水率和未冻水含量轻微下降或不变。说明水分迁移现象最明显且水分聚集最严重的部位在于冻结层本身，武夷山地区冻结层厚度约为10 cm。