大概念视角下复数乘法教学的问题设计*

杜志伟 孙传彬

(涡阳县第四中学 安徽亳州 233600)

一、问题的提出

数系从实数扩充到复数，乘法的运算性质保持不变，人教版教材在处理这部分内容时，直接给出复数的乘法法则，笔者在教学过程中，发现学生对这种“数学规定”产生了一定的困惑。究其原因，是学生在经历数系扩充的过程中，没有系统地理解这些“数学规定”。如何让学生理解复数乘法的“数学规定”呢？《普通高中数学课程标准(2017年版2020年修订)》指出，落实核心素养，需要更新教学内容，优化知识结构，重视以学科大概念为核心，使课程内容结构化。为此，笔者以“数系扩充中的数学规定”作为大概念，将复数的乘法法则作为主要内容，围绕大概念设计主要问题，实施单元教学。

二、单元教学整体设计

单元教学设计是以教材为基础，运用系统论方法对教材中“具有某种内在关联”的内容进行分析、重组、整合，并形成相对完整的单元教学设计。如何整合“具有某种内在关联”的内容，国内外很多专家把目光聚焦于学科大概念，以大概念为锚点，分析数学知识的结构，研究数学知识的本质。借鉴已有研究成果，本文采用“总—分—总”设计模式,主要设计路径如下：

《普通高中数学课程标准(2017年版2020年修订)》指出，本单元的学习，让学生理解引入复数的必要性，了解数系的扩充，掌握复数的表示、运算及其几何意义。具体内容包括：复数的概念、复数的运算、复数的三角表示。本章内容突出几何直观和代数运算之间的融合，重点让学生感悟数学知识之间的关联，加强学生对数学整体性的认识，从而培养学生数学运算和直观想象素养。

学科大概念是指能反映学科本质，具有广泛适用性和解释力的原理、思想和方法，它能将多样化的数学概念连接为统一的整体，从而避免当下教学设计过于注重单个知识点和学生学习过于碎片化的现象。本单元研究的主要问题是数系扩充过程中的新概念、数的表示、运算法则及其几何意义。在数系的扩充过程中，如何定义一类新的数，如何规定它的运算性质及其几何意义等，教材都做了规定，学生需要探究的是为什么这么规定以及这些“数学规定”的合理性。因此，将本单元的大概念提炼为“数系扩充中的数学规定”。

本单元的学习，学生要掌握复数的概念、表示、运算和几何意义，因而复数的学习可以类比实数的学习，二者的运算和几何意义，具有很多的相似性，如实数可以和数轴上的点建立一一对应关系，复数可以和平面上的向量建立一一对应关系，只是前者是一维的，后者是二维的。围绕大概念“数系扩充中的数学规定”，本单元教学目标设计如下。

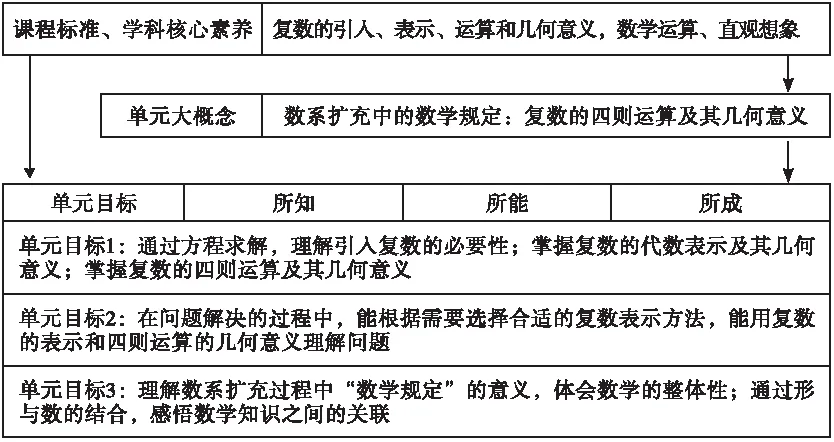
单元教学中如何渗透大概念，如何完成单元目标中的“所知、所能和所成”，需要教师设计基本问题。基本问题要具有明确的指向性和驱动性，指向大概念的理解和掌握，驱使学生具备理解大概念所需要掌握的知识和能力，最终发展其数学核心素养。下面以复数的乘法为例，设计单元教学基本问题。

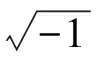
问题2 对于数列1,x,-1，你能否找到一种运算，将1转变为x，再将x转变为-1？

追问1 计算i，i2，i3的值，你发现了什么？这里面包含了什么运算？

追问2 从复数的几何表示出发，解释i·i的几何含义。

追问3 类比上面处理问题的方法，你能否解释1·i，1·i·i的几何含义？

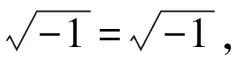
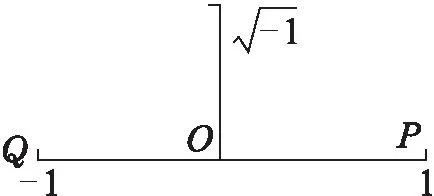
图1 复数的几何解释

问题3 你是如何理解教材中对复数乘法法则的规定的？

追问1 你在什么地方也遇到过这样的“规定”？

追问2 这些“数学规定”在某种程度上有没有共性？

追问3 这样的“数学规定”有什么意义？

从小学到高中有许多“数学规定”，如0乘任何数都等于0，a0=1，空集是任何集合的子集。如何将这些“数学规定”联系起来，帮助学生发现这些“数学规定”的共性和合理性，是本节课的教学难点。本节课以“数系扩充中的数学规定”作为大概念，引导学生探究小学、初中和高中遇到的“数学规定”。在学生畅所欲言后，教师可适当作一些归纳总结。数学课程中的“规定”具有一定的思想性：(1)确定性。如函数定义中的“确定性”是为了让函数模型符合实际，质数不包含1是为了保证任何一个合数分解成质数的形式唯一；(2)辩证统一性。在数系扩充的过程中，要让新的运算符合相应的规律或者规则，不能仅仅凭自身判断，如无理数指数幂、有理数指数幂运算遵循整数指数幂运算法则，规定20=1而不是0，是因为20=22÷22。

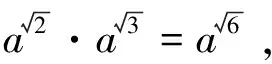
问题4 请探究复数乘法是否满足交换律、结合律和乘法对加法的分配律。

追问1 你将如何证明复数乘法的运算律？

追问2 结合实数和复数乘法运算律，再次感受“数学规定”的意义。

探究复数乘法运算律是研究一类新的运算的必经之路，课本以探究题的形式，引导学生发现并证明复数乘法的运算律。学生通过探究，不仅可以发现复数乘法的运算方法，同时还能发现复数乘法和实数乘法具有一定的一致性。在探究问题的过程中，教师要做好引导。以乘法的交换律证明为例，首先引导学生探究z1，z2，z3∈C，等式z1·z2=z2·z1是否成立？其次，以其中某一等式为例，引导学生尝试证明，并予以示范。学生在证明的过程中，将体会到复数的乘法要依托实数的乘法，同时这种严密的思维训练将为大学线性代数的学习打下基础。

问题5 试探究复数乘法的几何意义。

追问1 借助图形，表示复数加法的几何意义。

追问2 复数的乘法与向量有没有关系？请说明原因。

追问3 将1转变为x，再将x转变为-1时有没有出现乘法，乘的是什么？其几何含义是什么？

追问4 你觉得复数的乘法与什么有关？

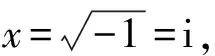
问题6 你能不能引进新的量来表示复数和复数的乘法？

追问1 如图(见图2)，设复数z满足|z|=r，∠xOz=θ，求复数z.(将复数z写成a+bi的形式)

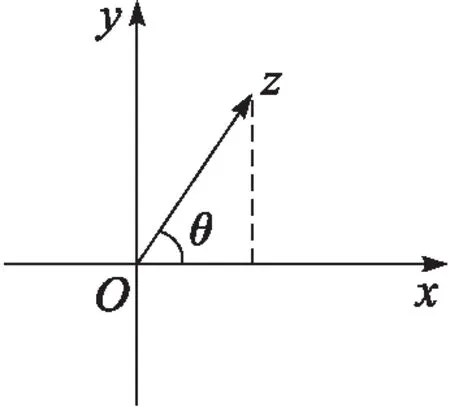
图2 复数的三角表示

追问2 已知z1=r1(cosθ1+isinθ1)，z2=r2(cosθ2+isinθ2)，求z1·z2。

追问3 用图形来表示追问2中的z1·z2。

追问4 复数的乘法的几何意义是什么？

追问5 设复数z满足(1+i)z=2i，求|z|.

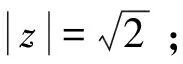
大概念单元教学评价以形成性评价为主，根据教师设计的表现性任务，重点关注学生的思考过程、行为表现和情感态度，即什么证据能表明学生或协作小组已经深入思考了这些问题，并表现出积极修订、积累经验的倾向。本单元的学习评价主要考查学生对数系扩充的理解水平，根据各层次的表现性任务，评价要点如下表(见表1)所示。

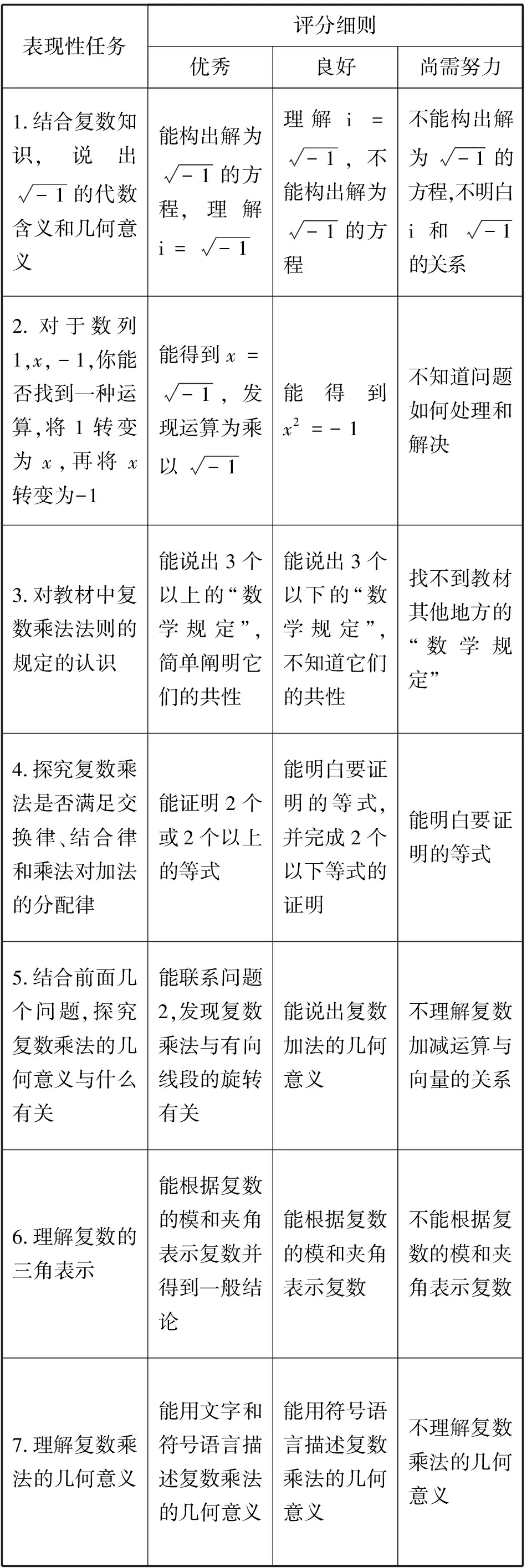
表1 学习评价表

三、课堂教学反思与建议

以大概念为核心的单元教学设计的主要特征有关联性和整体性，在复数乘法的单元教学设计中，以“数系扩充中的数学规定”作为大概念，将有理数到实数的扩充过程中的思想方法应用到本单元中，同时复数的乘法又将复数的几何意义、复数的加法和三角表示串联起来，促进学生整体上建构数学知识体系。

(一)以大概念为锚点，保证课程结构的完整性

数学知识之间具有严密的逻辑关系，且这种关系是一种具有层次的网状结构，以教材为主的单元(章节)和以发展学生核心素养为目的重组的“大单元”，在一定程度上能帮助学生探究数学知识间的关系，从而建构知识体系。如何组织单元教学，需要以学科大概念为锚点，不仅能在横向上精选知识，完善知识结构，而且能在纵向上促进小初高衔接。

(二)以基本问题为核心，提高学生的数学理解能力

如何在教学中落实核心素养？需要教师围绕大概念，设计促进学生理解大概念的基本问题。基本问题的设计要考虑学生的数学经验和生活经验，从学生的实际生活出发，联系学生已有的数学知识和方法，以促进学生概念进阶为目的，以发展学生数学核心素养为目标，选择恰当的问题、设置合理的表现性任务，帮助学生对知识进行选择、加工和处理，促进学生对数学知识的理解。