强迫对流下正庚烷浸湿多孔球的火焰结构与波动特征

张亚杰，穆志强，魏衍举，杨亚晶，刘圣华

(1.西安交通大学 能源与动力工程，陕西 西安，710049；2.西安交通大学 航天学院，机械结构强度与振动国家重点实验室，陕西 西安，710049)

喷雾燃烧是许多工业过程中的普遍现象，例如液体火箭发动机[1]、飞机发动机加力燃烧室[2]和使用液体燃料的内燃机[3]等场景中的燃烧。长期以来，尽管喷雾的行为并不完全像单个液滴的行为[3]，但单液滴仍被广泛用于指示和预测喷雾的行为。单液滴燃烧理论模型的研究开始于20 世纪50年代，GODSAVE[4]和SPALDING[5]提出了静态环境中单个液滴蒸发燃烧过程的D2模型，这种简化的燃烧模型是基于纯液滴蒸发模型得到的[6]。液滴燃烧模型经历了无限热导率定律[7]、一维球对称模型[8-9]、二维球对称模型[10-11]，最后发展为轴对称模型[12]，其复杂性逐渐增加。近年来，液滴燃烧实验得到了广泛的开展，但大多数实验是为了研究液滴燃烧特性。研究人员主要采用悬滴法探究了不同因素对不同类型纯燃料液滴和多组分混合燃料液滴燃烧特性的影响，如延迟时间、液滴寿命、微爆特性和碳烟产生等，或采用飞滴法，在高温环境下通过自燃或强制点火进行研究[13-19]。

然而，强迫对流条件下液滴燃烧的火焰结构与静态或准静态燃烧下完全不同。不同的火焰结构导致燃料液滴的不同汽化、燃烧和放热速率。为了预测和优化喷雾燃烧模型，有必要了解液滴对流燃烧的不同火焰结构和影响因素[19-21]。自20世纪60 年代以来，研究人员一直在研究液滴的火焰结构和多样性。在稳态燃烧的实验研究中，HIRSCHFELDER[22]使用液体燃料润湿的多孔球体来模拟燃料液滴。AGOSTON等[23]使用类似模型研究了强制对流条件下燃烧液滴的火焰，发现了三种不同的液滴燃烧火焰结构：包层火焰、尾流火焰和边界层火焰。基于AGOSTON等[23]的研究，CHIU[20]提出多结构的概念，即在给定的雷诺数和环境温度下燃料液滴存在多个火焰结构。MERCIER等[24]在研究丙酮液滴的羟基自由基在对流环境中的燃烧过程中，获得了其他的火焰结构即静态包层火焰和移动液滴周围的包层火焰。之后，李科等[21]利用一步总包有限反应速率模型模拟高温环境下的强制对流液滴燃烧，得到了全包络、半包络和尾焰三种火焰结构，这与MERCIER等[24]的一些实验结果是一致的。除此之外，HUANG等[25-26]对热塑性塑料形成的滴落火焰进行了研究，重点关注了其滴落尺寸以及自由下落过程的火焰脱落行为。

可见，自然对流下的燃料液滴燃烧研究取得了很大进展。然而，对强制对流下单个燃料液滴的火焰结构的研究还不够充分，尤其是在涉及高温下处于高强度强迫气流中的燃料液滴燃烧方面。为此，本文作者在温度为420～720 K 以及雷诺数Re=100～800 范围内气流强度下，对用正庚烷润湿的多孔球的火焰的时间平均结构特征和瞬时波动进行了研究，以阐明飞行燃料液滴的火焰结构的控制机制。

1 实验装置与方法

实验装置示意图如图1 所示。利用多孔球体(主要成分为硫酸钙，球直径d0=6 mm)模拟燃料液滴，用U 形针(直径为0.45 mm)将其悬置在热气流出口中心处，具体操作为将U 形银针从底部竖直插入，以避免其对流场产生干扰。而在实验前，热空气出口是被挡片遮挡的，以防止高速气流冲击造成点火困难。热电偶用于测量出口中心处的空气温度，并在将球体移入之前将其移除。实验步骤具体为：首先用正庚烷将多孔球充分浸湿并使其表面也覆盖一定厚度的燃料层，之后用电火花将其点燃，然后打开热气流出口(直径dol=40 mm)，开始观察火焰。

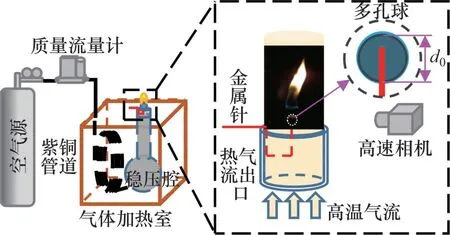
图1 实验装置示意图Fig.1 Schematic diagram of experimental devices

实验中的强迫对流环境由加热后的空气在压差力驱动下实现。具体实现方法为：瓶装压缩空气首先通过流量控制器(Sevenstar D07，0～120 L/min)调节以实现不同流速，然后流入位于马弗炉(Tmax=1 200 K@4 kW)中的盘绕多圈的紫铜管道以增加气流停留时间，之后进入球形稳压腔二次加热，最后均匀的热气流由钢制管道流出吹向火焰。如上操作，依次进行气流速度为0.6 m/s 至7.1 m/s(小球移入位置)，温度为423 K 到723 K(间隔为100 K)条件下的实验。实验中，使用高速相机(Phantom Miro eX4，4 000 帧/s)记录火焰，通过充分观察发现它经历了短暂的三个阶段，包括火焰发展、稳定燃烧和随着正庚烷耗尽而熄火阶段，本文重点关注稳定燃烧阶段。

需要申明的是，目前出口处的流速在高温下是无法测量的，它是用流量控制器的流速和当地温度通过式(1)得出的近似值。

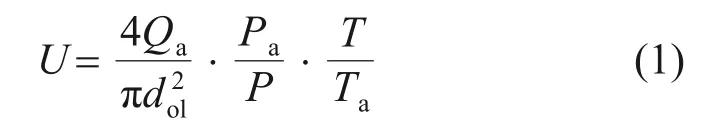
式中：U，P和T分别为管道出口处热空气的轴向流动速度(定义为对流速度)、压力和温度；Pa和Qa分别为通过流量计的空气压力和体积流量。热空气的黏度μ是关于温度的函数，由Suthenland 公式[27]计算得出，进而通过式(2)计算得到雷诺数Re。

在这项工作中，所有数据均是通过自编的Python-OpenCV 图像处理程序基于像素精度获得，此处数据误差可忽略不计。

2 实验结果与分析

2.1 火焰结构演变

图2所示为当T=420 K时随着对流强度的增加火焰结构演变的典型过程。

图2 随着对流强度增大火焰结构及位置的变化Fig.2 Transformation of flame structures and elevation of flame positions under the condition of forced convection

当U=0.6 m/s 时，存在一个具有明显正弦波动的全包火焰。随着对流强度的增加，火焰底部逐渐上升，火焰结构在U=0.9 m/s 时呈半包络状。当U=1.1 m/s 时，火焰底部平行于球体的南极，称为尾焰[24]。火焰的南极在U=1.2 m/s 时与球体完全分离，距球体的北极约4 mm，形成边界层火焰[24]。在上述过程中，火焰高度随对流强度增加而逐渐变短，但仍呈现正弦波动。与此同时，黄色火焰的区域逐渐缩小直至消失。而蓝色火焰区域经历了四个阶段：包络(U=0.6 m/s)、环状(U=0.9～ 1.2 m/s)、起伏环状(U=1.5～1.8 m/s)，最后随着波动加剧，火焰褶皱增加，成为一个褶皱的火焰并逐渐占据整个火焰体(U=1.8～3.5 m/s)，并且火焰不再有明显的正弦波动，而是闪烁波动。随着对流强度的增加，燃料和空气混合得更充分。即使有未燃烧的悬浮碳颗粒，也会很快被气流冲走。因此，火焰的主体逐渐只有蓝色区域。

2.2 火焰时均特征

为了量化分析火焰结构特征，定义量纲一火焰高度为

量纲一的火焰面积为

量纲一的火焰悬浮距离为

其中：S为多孔球最大截面积，

对于各个火焰参数的分析数据均采用火焰稳定阶段10个波动周期的时均值，计算方法为

其中：N为单个波动周期所含帧数；ds为悬浮高度，具体定义为火焰底部与多孔球北极点之间的距离。各个参数的具体定义见图3。

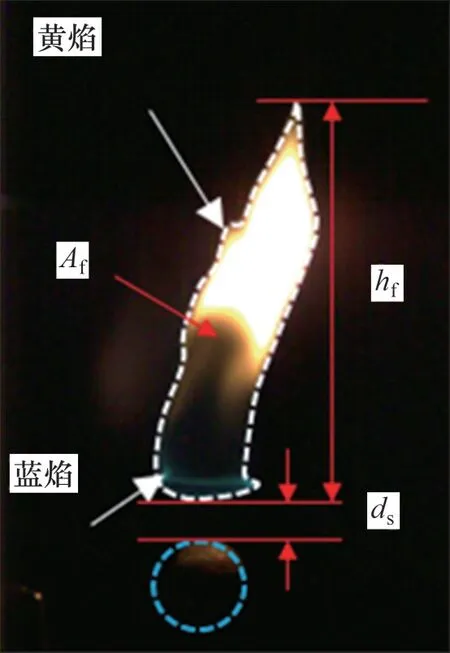
图3 关于火焰结构的几个参数定义Fig.3 Definition of flame overall properties

图4 所示为对流速度与温度对火焰结构的影响。从图4(a)和(b)可知：在低对流速度下，火焰高度为多孔球直径的12～16 倍(≈12～16)，而随着对流速度的增加，火焰高度逐渐缩短至多孔球直径的2倍这一定值。在这个过程中，火焰燃烧状态大致可分为两个阶段，即由黄焰占据主体转变为蓝焰占据主体。同时，随着对流速度增大，火焰悬浮距离近似等于多孔球直径后趋于稳定。此外，增加对流气流的温度会使上述转变过程向高流动速度方向移动，高温环境使得火焰传播速度加快，导致火焰对强对流的耐受性更好。而最后趋于稳定则是钝体绕流背风面的气流强度与火焰传播速度达到平衡的结果。

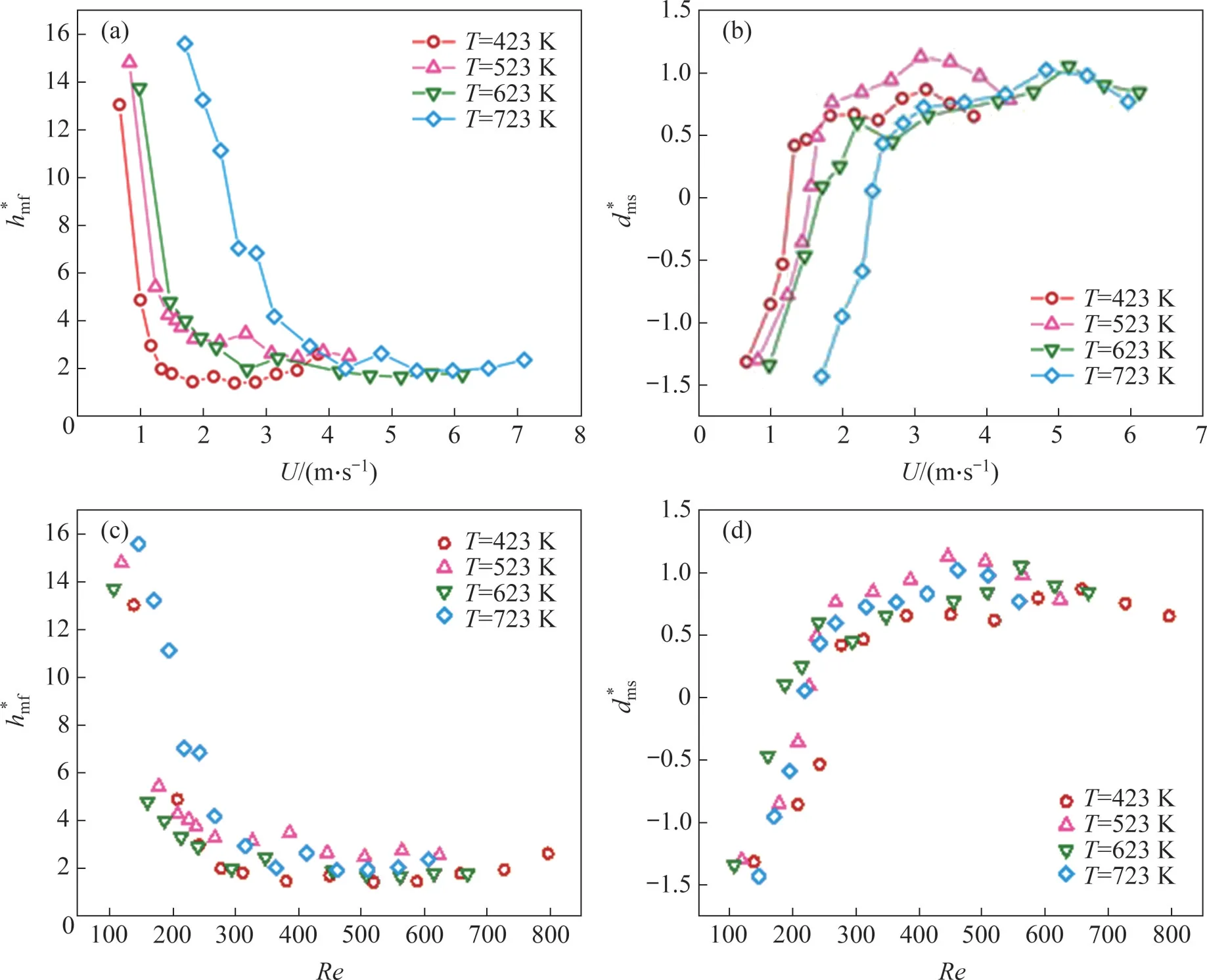
图4 不同对流速度和温度下的火焰结构Fig.4 Flame structures with different air flow velocities and temperatures

强迫对流中的液滴弱火焰是燃料蒸发、燃料/氧化剂传质、空气流动、点火、燃烧、火焰传播、放热和传热达到复杂物理化学平衡的结果。其中，温度是所有过程的促进参数，而较高的流速是火焰稳定性的抑制参数。在火焰燃烧过程中，温度和流动两种因素相互竞争。而雷诺数(Re=ρd0U/μ)比较适合作为评估火焰传播与吹熄之间竞争关系的判据，热空气密度ρ为

式中：ρa和Ta分别为标准状况下空气的密度和温度。

热空气黏度[27]μ为

式中：μa为标准状况下空气的黏度；B=110 K。因此，可以得到ρ∝T-1，μ∝T0.5，进而得到

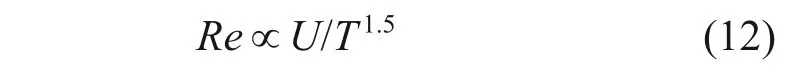
从图4(b)和(c)可知：不同温度对流环境中的量纲一火焰高度以及火焰悬浮距离的变化曲线均耦合在一起，这说明雷诺数Re是控制火焰结构转变的主导因素。并且，在火焰高度和悬浮距离的变化明显分为两个阶段，第一阶段分别为急剧减小和急剧增加，第二阶段则进入相对平稳，不再有明显的增加或减小，两个阶段的分界点雷诺数Re≈300。

火焰高度与悬浮距离之间的关系如图5 所示。从图5可知：火焰高度与火焰悬浮距离之间存在明显的负相关关系。当对流温度增加为720 K时，这种关系趋近于线性，符合式(13)所示的拟合关系式。

图5 火焰高度与悬浮距离之间的关系Fig.5 Relationship between and

图6 所示为火焰面积Amf以及蓝焰面积占比η与雷诺数Re之间的关系。从图6(a)可知：随着对流强度的增加，火焰面积的变化趋势与火焰高度的变化相似，即从急剧减小到趋于平稳，两个阶段分界点的Re依然为300左右。图3中，蓝焰区域会逐渐增加，最终整个火焰成为蓝焰，因此，进一步将火焰的蓝焰区域面积定义为Abf，并定义蓝焰面积占火焰面积的比例为

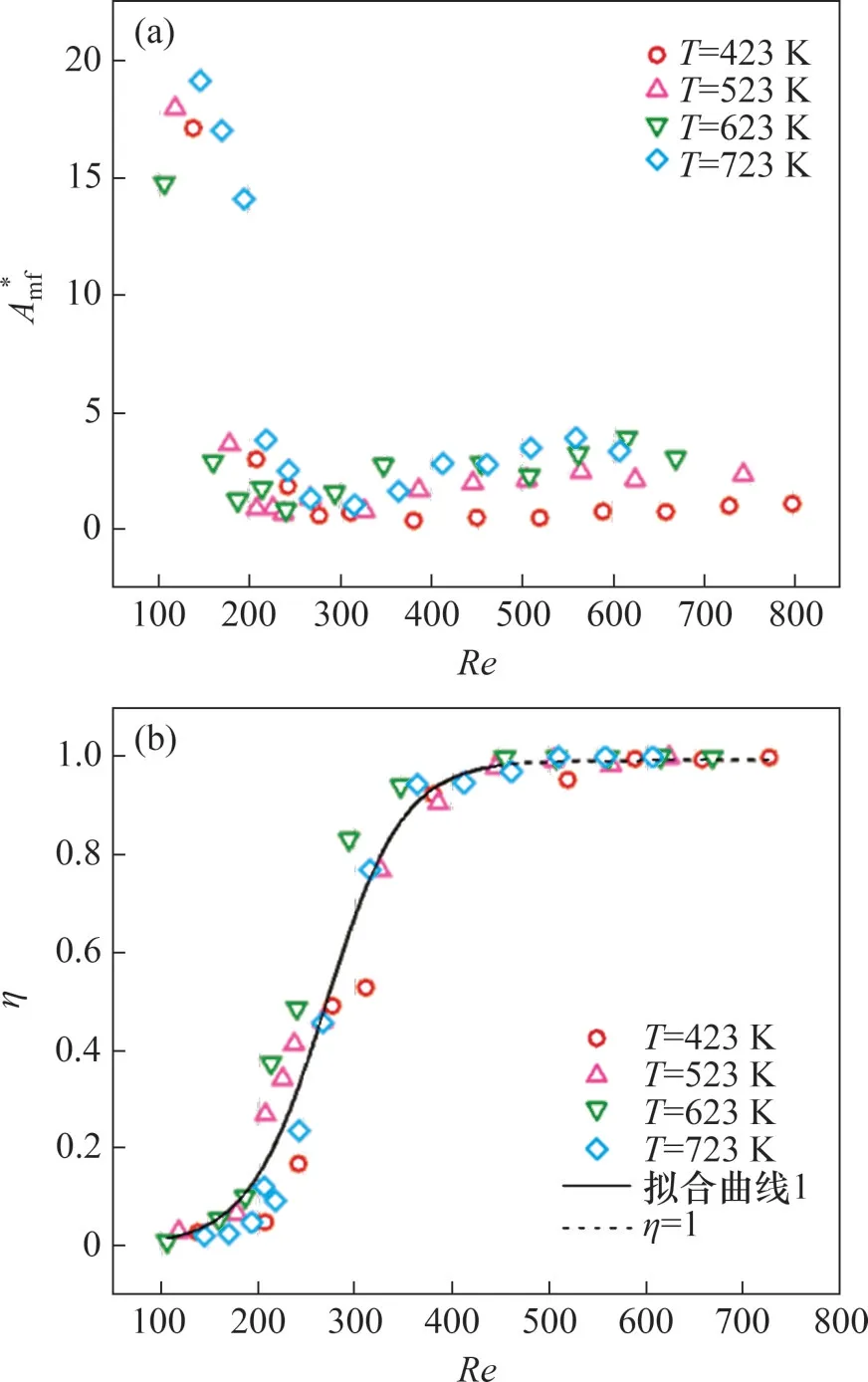
图6 火焰面积Amf以及蓝焰面积占比η与雷诺数Re之间的关系Fig.6 Relationship between area of flame Amf and ratio of blue flame area η versus Re

从图6(b)可知：火焰经历黄焰、过渡火焰再到蓝焰三个阶段，在这个过程中，Re为200和400分别为两个临界值。η随对流强度呈现阶跃型变化，符合式(15)所示阶跃函数关系。

2.3 火焰瞬时波动

在描述了火焰的时均特征之后，接下来对火焰周期性波动的频率进行分析以揭示其潜在机制。图7所示为火焰的瞬时波动。从图7(a)可知：当不对火焰施加强迫对流时，火焰波动模式是轴对称的。漩涡从火焰的根部发展，离开火焰主体后形成一个火焰孤岛，然后逐渐消失。火焰主体在漩涡分离后迅速收缩，然后又重新生长。在自然对流下，浮力火焰波动是由火焰与周围空气之间的黏性摩擦产生的环形涡流的周期性脱落引起的[28]，理论上自然对流下的扩散火焰波动频率可由式(17)[28]计算得出，约为19 Hz。

图7 火焰的瞬时波动示例Fig.7 Examples of flame flickering

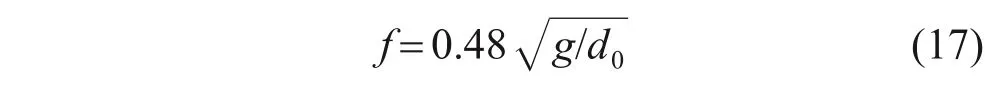
其中：g是重力加速度。

图8 所示为自然对流下浮力火焰的周期性波动。从图8(a)可见火焰瞬时高度hf的波动，其中红色实心点代表火焰孤岛形成的时刻，而黑色实心点代表孤岛消失的时刻。此外，波动频率f=16 Hz(图8(b))与YANG等[28]计算得到的理论值吻合较好。

图8 自然对流下浮力火焰的周期性波动Fig.8 Flickering of buoyant flame under natural convection

然而，强迫对流下的火焰波动模式与自然对流不同。当Re＜300 时，火焰呈类似于正弦波的非对称波动(图7(b))；当Re＞300时，火焰呈爆发式波动(图7(c))。

为了表征波动过程，选择某一固定维度上火焰能到达的最左侧位置的波动(定义为图9(a)中的xmin)进行分析。可见，xmin呈现周期性波动，进一步通过傅里叶变换得到波动频率(见图9(b))，当T=420 K时，主频率为31 Hz。

图9 当温度为420 K和对流速度为0.6 m/s时xmin对火焰波动的量化表征Fig.9 Quantitative characterization of flame volatility using xmin at T=420 K and U=0.6 m/s

在一个波动周期内，蓝色火焰先横向延展，然后向上波动，同时横向维度收缩。图10 所示为当温度为420 K 和对流速度为1.5 m/s 时，通过hf，xmin和Af对火焰波动浸渍进行量化表征。从图10(a)可知：水平坐标xmin、最大生长高度hf和火焰面积Af似乎都具有周期性。从图10(b)可知：通过上述方法得出的三种特征的波动频率是一致的。图11所示为各种对流速度下的波动频率。由图11 可见主频率随着流速U的增加而增加。

图10 当温度为420 K和对流速度为1.5 m/s时hf，xmin和Af对火焰波动的量化表征Fig.10 Quantitative characterization of flame flickering using hf,xmin and Af at T=420 K and U=1.5 m/s

图11 对流温度T=420 K时不同对流速度下火焰的波动频率Fig.11 Flickering frequencies of flames at various air flow velocities at T=420 K

由于火焰是钝体绕流和燃烧的综合效应，卡门涡旋的周期性脱落[29]可能是火焰周期性波动的原因。在100＜Re＜300时，可参照STRNIŠA等[30]和ZHANG等[31]对斯特劳哈尔数St的测量值，而在Re＞300 时，St=0.21[32]。用式(18)计算卡门涡旋的脱落频率fcar，如图12所示。从图12可知：卡门涡旋的脱落频率fcar与实验结果吻合较好，由此推断火焰波动是受St控制的涡旋脱落问题。

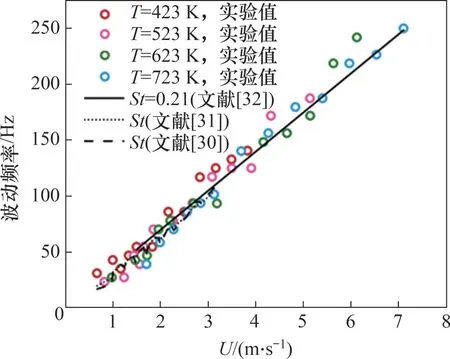
图12 波动频率实验值与理论值对比Fig.12 Comparison of experimental and theoretical flickering frequenties

3 结论

1) 在环境压力P=101 kPa 和各种强制对流条件(T=420～723 K和U=0.6～7.1 m/s)下，用正庚烷润湿的多孔球的火焰行为揭示了强迫对流其火焰结构演化和瞬时波动的控制机制。

2) 随着对流强度的增加，火焰底部逐渐抬升，直至悬停在球体北极上空某一高度处，期间火焰经历了全包围火焰、半包围火焰、尾迹火焰和边界层火焰的变化过程；火焰高度和面积逐渐缩小，最终稳定在一定范围内，此时火焰位于球体北极的背风区；Re=300 是火焰高度、悬浮距离和面积等火焰结构转变的临界点。同时，火焰高度和火焰悬浮距离之间在T=720 K 时符合明显的线性关系。黄色火焰区域的比例逐渐减少，最后完全变为蓝色火焰，且蓝色火焰比例变化符合关于Re的阶跃函数关系。

3) 分析了火焰结构的瞬时波动行为，并在Matlab 软件中通过傅里叶变换得到了频域分布结果。多孔球火焰的周期性波动特性在自然对流下符合浮力射流火焰涡流的动力机制。然而在强迫对流下，火焰波动频率由卡门涡的周期性脱落主导。