不同应力条件下含充填物砂岩的能量演化规律

谢成龙,吴秋红,翁磊,叶洲元

(1.湖南科技大学 资源环境与安全工程学院,湖南 湘潭 411201;2.湖南科技大学 煤矿安全开采技术湖南省重点实验室,湖南 湘潭 411201;3.湖南科技大学 南方煤矿瓦斯与顶板灾害预防控制安全生产重点实验室,湖南 湘潭 411201;4.武汉大学 土木建筑工程学院,湖北 武汉 430072)

岩石的破坏归根到底是能量驱动下的一种状态失稳现象[1].当前,随着深部开采活动越来越频繁,积聚在岩石内部的高能量被释放出来,导致围岩失稳破坏的现象时常发生,如岩爆、顶板大面积来压等灾害现象,给人员及设备的安全带来了严重威胁[2-3].因此，研究岩石在不同应力条件下能量演化规律具有一定的理论和工程应用价值.

目前,不少学者研究岩石在不同加载条件下的能量演化规律.谢和平院士等[4]基于能量耗散强度丧失准则和可释放能量的岩石整体破坏准则,得到不同应力状态下岩石整体破坏的临界应力;王桂林等[5]研究单轴压缩条件下节理倾角、长度以及围压对节理砂岩峰前宏细观能量自我抑制演化的影响,发现峰前宏细观能量自我抑制作用与节理长度成正比,与围压水平成反比;张国凯等[6]通过岩石单轴压缩试验,发现应变能、耗散能、摩擦能峰值前后的变化规律;刘鹏飞等[7]发现围压对花岗岩力学特性的影响,以及不同围压条件下岩石损伤的变化情况;刘之喜等[8]研究白砂岩的能量演化规律,发现部分滞回效应耗散能与荷载呈正相关,荷载越大,耗散能越大,并分析弹性能与耗散能的比值关系.

厚壁圆筒试验作为研究岩石非均匀应力状态的常规方法,被广泛应用于岩石力学试验中.吴秋红等[9]研究了不同截面形状的砂岩试样的力学特性,发现方形与圆环形状的横截面对岩石力学特性及声发射活动的影响较大;张后全等[10]基于岩石厚壁圆筒卸荷试验,分析厚壁圆筒卸载环向断裂与分区断裂的关系,发现岩石破坏的新形式,其环向主要破裂面会在壁间产生;候公羽等[11]采用厚壁圆筒试样模拟开挖卸荷和破坏试验,分析轴向应变与切向应变在卸荷过程中的变化情况,发现围岩试件的破坏路径与破坏形态;周喻等[12]探究厚壁圆筒在不同内、外部围压作用下的破坏机制,发现在不同内部围压作用下试样的破坏形式是不同的,且试样承受的极限外部围压与内部围压成正比.

综上所述,学者们从不同方面对岩石能量演化规律进行研究,并且取得了一定的研究成果,但对厚壁圆筒相关的能量演化规律的研究很少.为此,本文采用含充填物砂岩试样,对其进行单轴压缩和常规三轴压缩试验,在文献[13]的基础上,探究不同应力条件下岩石的能量演化规律.

1 试样制备与试验方法

试验试样为长沙砂岩,砂岩呈灰色,颗粒中等,均匀性好.首先将完整砂岩样品取芯,取出直径为50 mm,高度为100 mm的圆柱体试样,然后加工成内径为16 mm的空心圆柱体试样,采用2种不同配合比的水泥砂浆来填充内孔,如图1a所示.低强度试样的水泥砂浆质量配合比为1∶5.27∶1.16(m水泥∶m砂∶m水),高强度试样的水泥砂浆质量配合比为1∶3.47∶0.64(m水泥∶m砂∶m水),具体参数如表1.为便于统计,完整、空心、低强度充填及高强度充填试样采用SC,HC,LF,HF进行标记.需要注意的是砂浆两端比岩石加载面略低于2.5 mm,以防止加载期间与底板直接接触.配好后将充填试样放入温度为25 ℃,相对湿度为95%的养护箱中养护28 d.试验采用了液压伺服控制的RMT-150C测试系统进行单轴压缩和常规三轴压缩试验(图1b).单轴压缩试验,采用位移控制方式,加载速率为0.002 mm/s.常规三轴压缩试验,设置了4种围压水平(5 ,10 ,20 ,30 MPa),试验采用压力控制方式,围压加载速率设置为0.1 MPa/s.

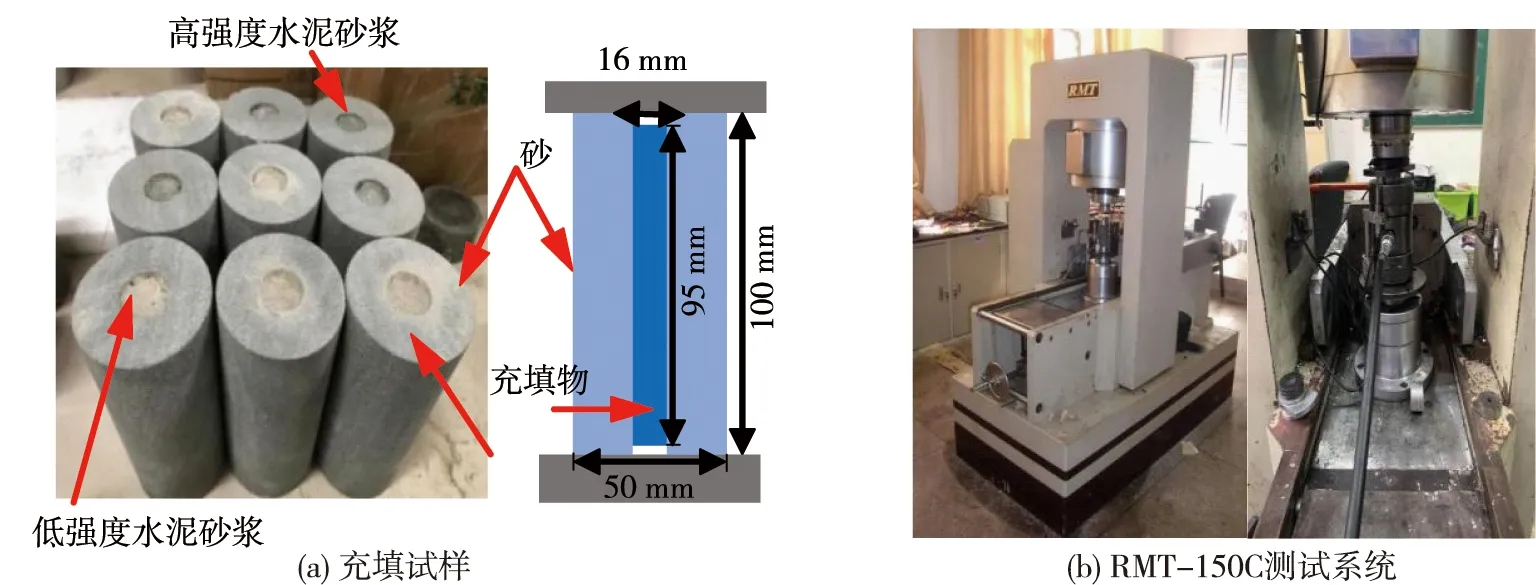
图1 试样制备与试验方法

表1 水泥砂浆与砂岩的物理力学性能

2 能量计算方法

假定岩石处于封闭系统中,与外界环境无热量交换,当受到试验机加载产生变形破坏时,可基于热力学第一定律[4,14-15],得到总输入能量U的计算公式如式(1).

U=Ue+Ud.

(1)

式中:Ue为弹性应变能;Ud为耗散应变能.

图2为试验过程中弹性应变能Ue与耗散应变能Ud的关系,其中σ1为轴向应力,ε1为轴向应变.

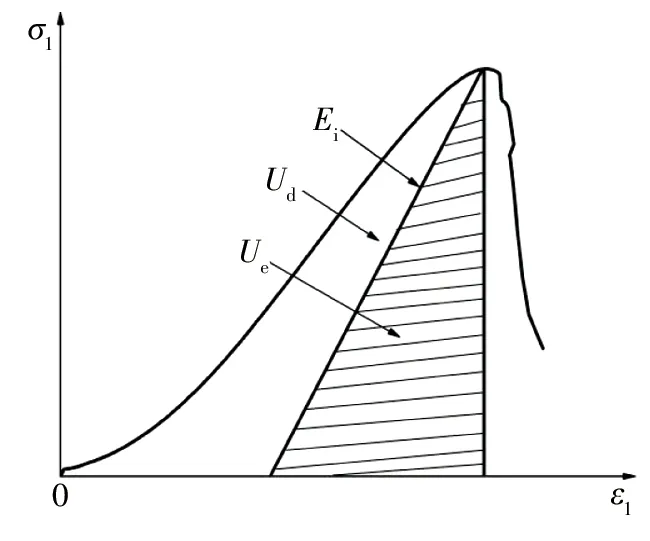
图2 试样加载过程中耗散应变能Ud与弹性应变能Ue的关系

根据广义胡克定律得到:

(2)

式中:σ1,σ2,σ3分别为最大主应力、中间主应力、最小主应力;ε1,ε2,ε3分别为最大主应力、中间主应力、最小主应力对应的应变;Ei为岩石卸荷弹性模量,根据尤明庆[16]以及黄达等[17]对大理岩试样试验研究结果得出可将Ei近似用初始弹性模量E来代替计算;vi为泊松比.

单轴压缩加载时,即σ2=σ3=0,式(2)可简化为

(3)

常规三轴压缩试验,静水应力加载状态试验机对岩样做正功,达到确定的静水应力后,轴向应力σ1增大持续对试样产生压缩变形,轴向应力σ1对试样做正功;而环向主要产生的是膨胀变形,围压σ3对试样做负功.总应变能U的公式为

U=U1+U3+U0.

(4)

静水应力下吸收的应变能U0可根据弹性力学公式求得

(5)

式中:U1为轴向应力σ1对围岩做正功的应变能;U3为围岩做负功的应变能;U0为静水压力下吸收的应变能;v,E分别为初始泊松比和弹性模量.

岩石受载过程中,轴向应力σ1对围岩做正功的应变能U1和围压做负功释放的应变能U3可根据应力-应变曲线积分得到[18]:

(6)

(7)

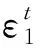
根据式(1)与式(4)得到耗散应变能Ud的计算公式为

Ud=U1+U3+U0-Ue.

(8)

3 单轴压缩试验

根据以上公式对试验数据进行处理,得到试样单轴压缩过程的能量特征如表2所示.从表2可以看出完整、空心、低充填、高充填这4种试样峰值前弹性应变能平均值分别为235.51,204.05,222.93,215.72 kJ·m-3,Ue/U(弹性应变能Ue与总能量U的比值为吸收比)平均值分别为0.80,0.84,0.84,0.88,耗散应变能平均值分别为58.67,39.12,43.20,29.45 kJ·m-3,Ud/U(耗散应变能Ud与总能量U的比值为耗散比[18])平均值分别为0.20,0.16,0.16,0.12.结果表明试样峰值前是以吸收弹性应变能为主,只有少部分能量用于内部微裂隙闭合摩擦、微裂纹扩展、破裂面相互贯通等.

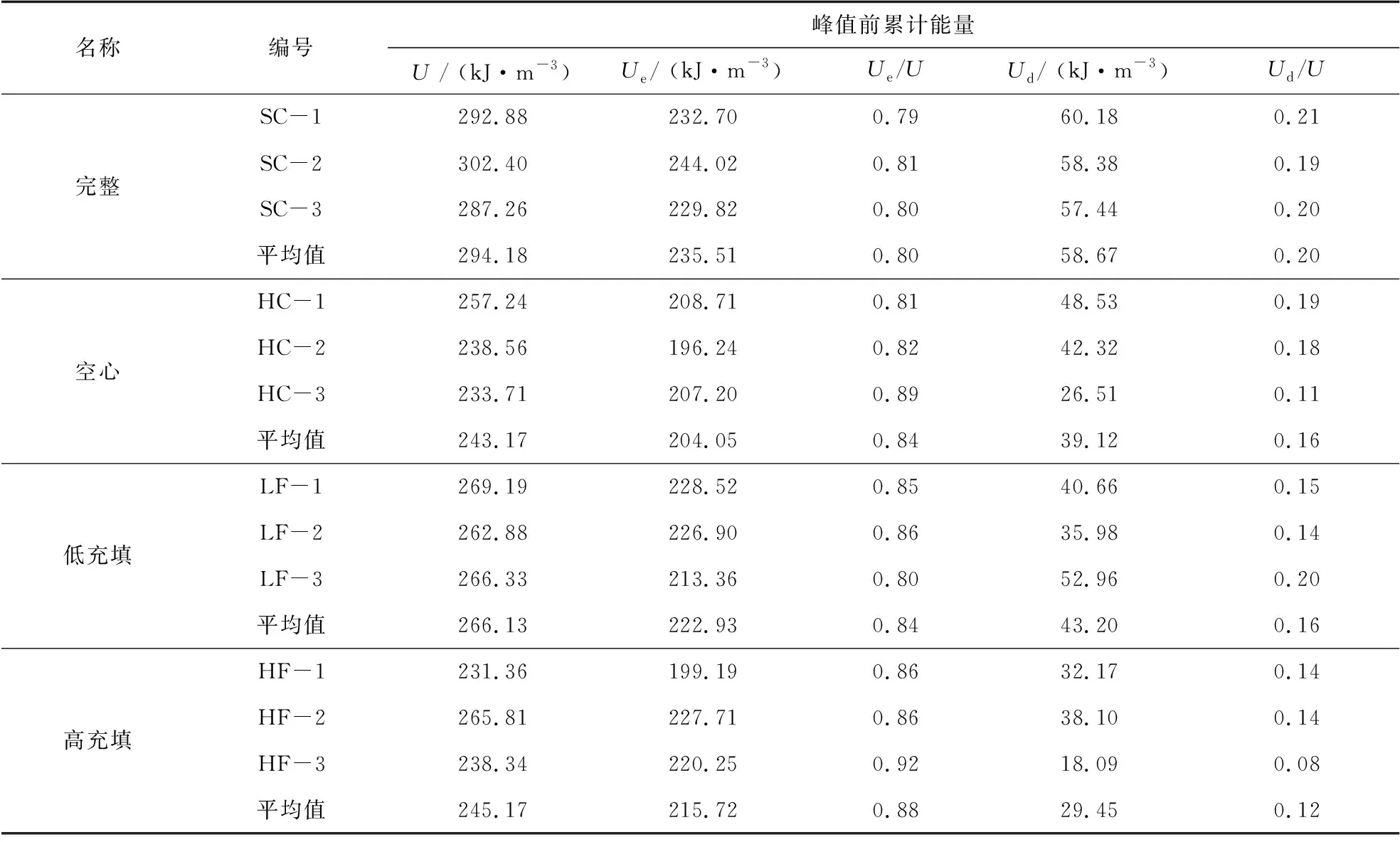
表2 试样单轴压缩过程的能量特性

基于热力学定律,得到单轴压缩过程中能量的转化关系(图3).以下是从完整试样、空心试样、低充填试样和高充填试样的压密阶段(OA)、线弹性阶段(AB)、屈服阶段(BC)和破坏阶段(CD)这4个阶段对能量进行具体分析.

1)压密阶段(OA):即初始非线性阶段,轴向应力约占峰值强度的30%以内.此初始阶段所产生的能量较少,各能量间的转化效率偏低.完整试样、空心试样、低充填试样、高充填试样的总能量、弹性应变能和耗散应变能随着载荷的增加呈缓慢增长趋势,且耗散应变能和弹性应变能差距不大.

2)线弹性阶段(AB):应力应变曲线近似直线的阶段,轴向应力约占峰值强度的30%～80%.此阶段试样从外界吸收能量并以弹性应变能的形式储存于试样内.随着载荷增加,总能量和弹性应变能呈线性增长趋势,其中完整试样、低充填试样、高充填试样的增幅较大(图3a,图3c,图3d),空心试样的增幅最小(图3b).相反,4种试样的耗散应变能几乎没有增加甚至出现明显的下降,这说明了试样的裂纹或裂隙被进一步压密,试样不断地吸收弹性应变能,弹性应变能占比较大.

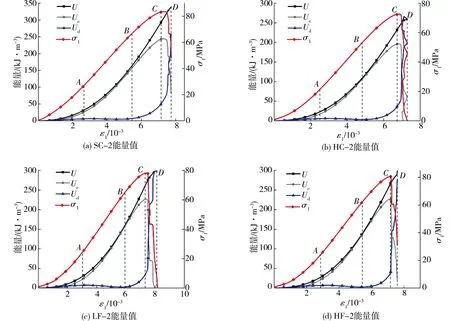
图3 应力-应变与能量转化关系曲线

3)屈服阶段(BC):轴向应力超过峰值强度的80%.此时试样吸收的弹性应变能基本转化为微裂纹扩展的耗散应变能,弹性应变能、耗散应变能都随着载荷的增加而增加,但弹性应变能的增长速率明显变慢(图3b).这说明了随着载荷的增加,试样内部结构发生了变化,变形增加,能量转化关系逐渐复杂.

4)破坏阶段(CD):即应力峰值后加速破坏阶段.由于微裂纹加速扩展、贯通,储存于试样内部的弹性应变能大部分转化为耗散应变能,并以摩擦能、动能等形式被释放出来.随着峰值后应力急剧下跌,弹性应变能也开始急剧减少,耗散应变能逐渐增长,且增长幅度较大,耗散应变能和弹性应变能曲线存在部分“重叠”现象(图3c),并且耗散应变能曲线逐渐向总能量曲线靠近直至试件破坏.

从图3可以看出：在峰值点C之前,总能量、弹性应变能都随着载荷的增加而增加,且经历了非线性到线性的增长过程,试样加载前期主要以吸收弹性应变能为主,耗散应变能基本保持不变甚至还出现了下降的现象.当达到屈服阶段时,由于微裂纹进一步的扩展,耗散应变能开始缓慢增加,耗散应变能曲线也逐渐上升.在峰值点C之后,弹性应变能达到最大值,随着加载过程的进行,内部大量的弹性应变能转化为耗散应变能.此时应力-应变曲线中应力急剧下跌,弹性应变能曲线急剧下降,相反,耗散应变能曲线急速上升.

由此看来,试样加载破坏过程经历了能量吸收、储存、耗散以及释放,在应力到达峰值前,试样以吸收弹性应变能的形式,储存能量,到达应变峰值后,试样以释放弹性应变能的形式,耗散能量.这与候永强等[19]的研究一致.

4 三轴压缩试验

4.1 三轴压缩能量演化规律

图4为不同围压下部分试样的能量演化特征,由于加载的试样较多,这里以完整试样(SC)为例,其中U,Ue,Ud,U3分别表示总能量、弹性应变能、耗散应变能以及围压做负功耗散的应变能.

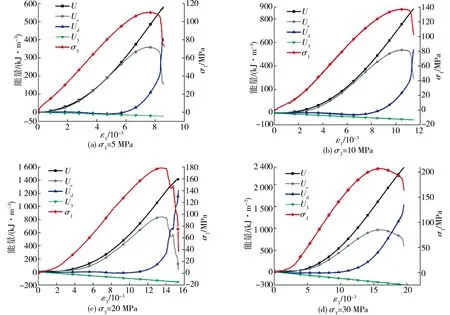
图4 不同围压下应力-应变与能量转化关系曲线

1)压密阶段.此阶段试样内部微裂隙发生初步闭合、摩擦滑移,吸收、储存的能量较少,各种能量间的转化效率偏低.初始压密阶段,弹性应变能呈非线性缓慢增长,耗散应变能、围岩做负功耗散的应变能基本保持不变,但随着围压的增大,围岩做负功耗散的应变能逐渐增加,当σ3=30 MPa(图4d)时增长幅度最大.此阶段试样未产生明显的变形破坏.

2)线弹性阶段.此阶段试样微裂隙由于已经被压密,开始产生新的微裂隙并逐渐向四周扩展.此时,随着荷载的增加,总能量和弹性应变能呈线性增长,围岩做负功耗散的应变能也呈直线增长,在σ3为5,10 MPa(图4a,图4b)时,耗散应变能基本保持不变甚至有下降的趋势,但随着σ3的增加耗散应变能开始逐渐增大,当σ3=30 MPa(图4d)时变化最为突出.

3)屈服阶段.此阶段试样微裂隙迅速扩展并相互贯通.耗散应变能随载荷的增加而增加,弹性应变能曲线仍继续保持增长,但增长速率明显变缓,其中在σ3=30 MPa(图4d)时增速变缓最为明显.当应力达到峰值过后,由于能量耗散,岩石内部结构发生较大变化,微裂隙大量发展、汇合.

4)破坏阶段.此阶段随着岩石微裂隙的持续扩展、汇合、贯通等作用,试样发生宏观破裂.弹性应变能曲线呈下跌趋势,弹性应变能所占的比例逐渐减小,相反耗散应变能曲线直线上升,向总能量曲线靠拢.围岩做负功耗散的应变能仍然显著增加直至停止,这些耗散能以表面能、动能等形式被释放出来,最终试样失稳破坏.

常规三轴压缩试验与单轴压缩试验相比,在能量转化方面具有相似之处,在应力达到峰值点之前,试样加载过程主要以吸收、储存弹性应变能为主,总能量、弹性应变能都逐渐增加,耗散应变能基本保持不变或增长缓慢.在峰值点之后,试件内部结构发生变化,试件加载过程主要以耗散、释放弹性应变能为主,弹性应变能急剧下跌,耗散应变能呈线性增长.不同的是,三轴试验有做正功、负功的情况,能量的转化更加复杂多变.

与此同时,从图4可以看出：随着围压的增加,能量转化过程更加剧烈,转化速率加快,围压越大,吸收、储存、耗散、释放的能量也就越多,试样轴向应变越大,应力达到峰值点的强度也越大.

4.2 U,Ue,Ud,Ud/U能量变化分析

基于试验的相关数据,我们对不同围压下4种试件(完整试样、空心试样、低充填试样、高充填试样)的U,Ue,Ud进行分析,得到如图5所示的柱状图.

1)如图5a所示,在同一围压下,完整试样的总能量U最大(如σ3=30 MPa时,最大值为1 478 kJ·m-3),空心试样最小(如σ3=30 MPa时,最小值为1 157 kJ·m-3),这是由于空心试样强度较低,自身承载能力相对较差,在试样加载前期产生的能量较少,能量转换率也偏低.在σ3为0和5 MPa时,低充填试样的总能量(如σ3=0 MPa时,低充填试样为266 kJ·m-3)是略高于高充填试样(如σ3=0 MPa时,高充填试样为245 kJ·m-3),但随着围压的增大,高充填总能量开始逐渐高于低充填(如σ3=30 MPa时,低充填试样为1 210 kJ·m-3,高充填试样为1 415 kJ·m-3)且增长幅度大,这说明了高充填试样对围压的敏感性更强.

在不同的围压下,随着围压的增大,4种试样的总能量都呈线性增长趋势,说明围压的增大对能量的吸收、储存、耗散、释放的全过程具有一定的影响.

2)如图5b所示,在同一围压下,完整试样的弹性应变能Ue最大(当σ3=30 MPa时,最大值为965 kJ·m-3),其他3种试样弹性应变能相差不大.在不同围压下,4种试样的弹性应变能与围压强度呈正相关,即围压越大,弹性应变能越大.

3)如图5c所示,在同一围压下,当σ3为0,5,10 MPa时,完整试样耗散应变能最大,低充填试样次之;而当σ3=20 MPa时,高充填试样耗散应变能最大(280 kJ·m-3),低充填次之(249 kJ·m-3),空心试样最小(72 kJ·m-3);当σ3=30 MPa时,完整试样与高充填试样耗散应变能相互接近,空心试样与低充填试样耗散能相互接近.因此在同一围压下,4种试样的耗散应变能起伏不定,较高强度的充填体对试样整体强度的提升具有明显的作用.在不同围压下,完整试样、低充填试样、高充填试样的耗散应变能随着围压的增加呈非线性增长趋势,空心试样耗散应变能经历了从增加到减少再到增加的过程,但总体上耗散应变能是增加的.

4)如图5d所示,当σ3=0 MPa时,高充填试样的耗散比最小(0.12), 随着围压的增大,当σ3=30 MPa时,高充填试样的耗散比达到最大值(0.35).与此同时,低充填试样也表现出同样的增长趋势.可以看出围压越大,含充填物试样的耗散比越大.

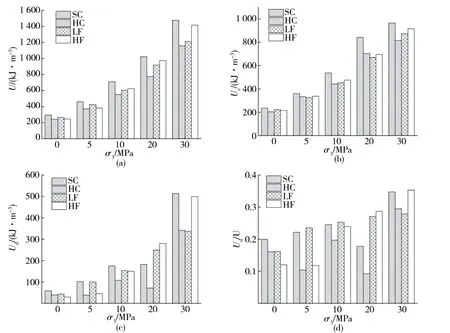
图5 不同围压下4种试件能量变化规律

5 结论

1) 在应力到达峰值前,四种试样都以吸收弹性应变能的形式储存能量,到达应力峰值后,4种试样都以释放弹性应变能的形式耗散能量.

2) 围压为0,5 MPa时,高强度充填试样的耗散比较小.随着围压的增大,含充填物试样的耗散比逐渐增大.

3) 4种试样的总能量、弹性应变能、耗散应变能与围压强度成正比,围压越大,其能量越大.

4) 与低充填试样相比,高充填试样对围压的敏感性更强,当围压增大,高充填试样能量的增长幅度明显加快.