三角波场源航空瞬变电磁测量的高度校正方法分析

田达志，杨 柳，杨 望，要悦稳，翟伟林，李金富，安 娜

(1.中国冶金地质总局地球物理勘查院，河北保定 071051；2.中国冶金地质总局矿产资源研究院，北京 101300)

0 引言

国际上航空电磁测量技术经历了70多年的发展，不仅在地质找矿工作中取得了成果，而且在工程地质、水文地质等方面也得到成功运用(Palacky，1981；Hyvarinen，1998；Christensen et al.，2009；丁志强等，2012；Chen et al.，2014；Patrick，2014；殷长春等，2015；殷长春，2018)。2010年以来，我国航空物探测量引进国外的时间域航空瞬变电磁测量系统，在国内完成了多个航空瞬变电磁测量项目，开创了我国航空物探的新局面(昌彦君和张桂青，1995；李永兴，2010；丁志强等，2012；梁盛军等，2014；刘冲等，2014；彭莉红等，2019；宁媛丽等，2020)。为了发展我国的航空电磁法测量事业，国内多位物探专家、学者开展了航空电磁法测量研究工作，取得了大量技术成果。但是我国的航空电磁测量技术有待进一步完善，数据处理方法仍未形成较统一的认识(苏朱刘等，2004；杜庆丰等，2006；刘祥平和王建明，2011；李肃义等，2013；陈斌等，2014；岳望，2018)。其中航空瞬变电磁场由于衰变的复杂性，其随发射距离的衰减规律仍有不同认识，实测航空瞬变测量数据的处理方法仍有待探讨，本文仅对航空瞬变电磁测量数据处理过程中的高度校正处理方法进行讨论分析。

目前我国引进的航空瞬变电磁测量系统一般要求测量飞行时吊舱(即发射线圈和接收线圈安装平台)离地高度控制在30 m左右平飞，以保证收发线圈与大地之间的距离基本不变。但在实际生产飞行中，由于地形的起伏或地面障碍物的存在，气流的变动，吊舱离地高度存在较大的变化，因此会引起吊舱中收发线圈与大地之间的距离发生较大变化，测量到的电磁响应信号强弱也随之变化，即接收线圈中的二次感应磁场的强弱也会随吊舱的离地远近发生明显变化，从而形成干扰异常。为了消除吊舱离地高度对电磁响应信号的影响，以获取地质体引起真实的电磁响应信号，需要把每条测线的实测数据按某种衰减规律统一换算到一个离地高度上来，对实测数据进行统一的高度校正。

1 高度校正理论基础

以发射场源为三角波的TS150直升机航空瞬变电磁系统为例，该装置属于水平共面(HCP)航电测量系统，发射电流波形为三角波，电磁场波形见图1。按照牛之琏的《时间域电磁法原理》中的分类，三角波激发场源也属于瞬变电磁法(牛之琏，2007)。

图1 三角波场源航空瞬变电磁系统激发电磁场波形示意图Fig.1 Diagram of electromagnetic field waveforms excited by airborne transient electromagnetic system with triangular- wave field source

目前，我国航空瞬变电磁波测量理论认为，接收线圈的电磁场为真空全空间中磁偶电流和下半空间涡流效应的和，一般采用G-S变换算法做逆拉氏变换计算感应电动势。例如以层状大地为模型，采用G-S变换推导了水平共面型航电装置的正演计算公式和算法(罗延钟等，2003；毛立峰等，2011；闵刚等2012)。该方法的理论模型设定为收、发线圈的尺寸相对其到地面距离小到可以看成磁偶极子，因此存在接收线圈中的感应电动势与目标地质体激发的二次磁场在时间上有如下关系：

(1)

式(1)中：V为接收线圈中的二次感应电压(单位：v)；SR为接收线圈面积(单位：m2)；dB/dt为接收线圈中二次磁场变化率，Gs/s；μ0为磁导率，μ0=4π×10-7H/m。为计算时间域电磁场，采用先在拉普拉斯变换域中作计算，再借助G-S概率变换算法做逆拉氏变换计算电磁场的瞬变过程，最终可求得接收线圈的感应电动势瞬时响应公式：

(2)

式(2)中：n是决定于计算机位数的正偶整数，取n=12，Km是G-S变换系数，t是时间(单位：s)，计算公式如下:

(i-1)!(m-1)!(2i-m)!]}

(3)

采用式(3)计算可以得到12个Km值，再代入式(2)计算感应电动势。通过这种理论计算方法，闵刚等(2012)研究了三层大地模型对飞行高度变化的时间域航空电磁响应的影响，其结论是飞行高度的变化直接影响测量到的电磁响应值大小，用这样的数据直接来做电阻率深度成像将产生干扰异常，但没有提出采用何种数据处理方法来消除飞行高度变化对电磁响应大小影响。

为了消除飞行高度变化对接收线圈中电磁响应大小的影响，一种观点认为航空瞬变电磁场激发的空间磁场强度随测量距离是按3次方幂指数衰减的，应以3次方幂指数衰减进行测量距离的高度校正；第二种观点认为和频率域的谐变场相似，航空瞬变电磁场也随距离呈近似指数规律衰减。

1.1 3次方衰减理论

航空瞬变电磁法的测量电磁信号不同于地面瞬变电磁法，地面瞬变电磁法研究的是半空间瞬变电磁波的传播特征，航空瞬变电磁法由于是在空中发射和接收信号的，需要考虑全空间瞬变电磁波的传播与信号衰减。均匀全空间中的阶跃电流断开时的时间域电磁场磁场Z分量的表达式有：

(4)

(5)

公式(5)即为早期全空间条件下垂直磁偶源产生的瞬变电磁场强度公式，可以看出在瞬变场中早期磁场的强度与测量距离的3次方成反比。同样，在频率域电磁法中，当ω→0，其感应磁场强度也存在上述磁场强度公式(5)，与测量距离的3次方成反比的关系。因此，可以认为瞬变电磁场电源激发的一次感应磁场强度与吊舱的离地高度呈3次方衰减，其激发的二次场强度也应按3次方规律衰减。

1.2 指数衰减

而依据平面电磁波的空中传播理论，在无限均匀介质中传播方程：

(6)

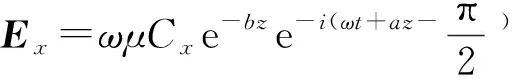
(7)

在此电磁场理论基础上，傅良魁等(1991)编制的电法勘探教科书中指出频率域电磁场在地面下随深度的衰减规律为按指数规律衰减，即：Ex(ω)=Ex0(ω)e-kz，这与沿空中Z轴方向平面波方程的衰减规律式(7)是一致的。因此，可以推断频率域电磁场的空中与地下的衰减规律也具有相似性，也应为指数规律衰减。此外，王卫平和王守坦(2003)也指出在均匀大地上方，各种装置的航空电磁响应与飞行高度之间为近似指数关系。

TS150航空瞬变电磁系统发射电流波形为三角波，根据傅里叶频谱分析理论，任何一种脉冲波都可分解成多个正弦波或余弦波成分。依据傅里叶变换可知，图2所示三角波的傅里叶级数为：

图2 周期三角波形示意图Fig.2 Diagram of periodic triangular waveforms

(8)

式(8)中:A为发射方波电流的基波电流幅值(单位：A)，ω为电流基波的频率(单位：Hz)，t为时间(单位：s)。从式(8)的傅里叶级数可以看出，三角波场源的瞬变电磁场为基波和多个奇次谐波电磁场综合反应，由式(8)中各项正弦函数的幅值系数可知，其与ω倍频率系数(2n-1)的平方成反比，频率越高，幅值衰减越快，因此7ω频率的谐波幅值衰减比基波衰减快得多，三角波场源7次谐波的电流幅值仅基波幅值的1/49(表1)，相对于基波的幅值小到可以忽略。地面瞬变电磁法测量规范均方差的无位差要求小于10%即可，三角波场源的3次谐波的电流幅值只有基波的1/9，所以三角波瞬变场的衰减特征只考虑基波和3次谐波的衰减特征就够了。为了简便快速计算，甚至可以忽略3次谐波，其衰减特征与频率域电磁场的衰减特征相近。此外，傅良魁等(1991)基于原长春地院M-1瞬变航电仪测量试验的基础上，也曾经指出“由于场的复杂性，瞬变衰减规律很难用一种数学式表达”，但一般可近似地用指数规律描述(李金铭，2005)。因此，三角波场源的航空瞬变电磁测量系统的电磁响应信号也可以认为是随着吊舱离地高度的变化呈现近似指数规律衰减的。需要指出的是，依据方波的傅里叶变化级数公式:

表1 三角波傅里叶级数中各级谐波参数比表Table 1 Harmonic parameter ratios of all triangular-wave Fourier series

(9)

式(9)与式(8)相同，A为发射方波电流的基波电流幅值(单位：A)，ω为电流基波的频率(单位：Hz)，t为时间(单位：s)。从公式可以看出，方波场源瞬变场因奇次谐波电流幅值递减较三角波场源慢很多，即使到9次谐波频率时，其电流流幅值仍为基波的1/9，奇次谐波所占的能量远比三角波的谐波大，因而在理论上方波场源瞬变场的衰减特征与三角波瞬变场的衰减特征存在较大差异。本文仅就三角波场源的瞬变场指数衰减规律的进行分析讨论。

2 两种校正方法的衰减系数差异

按航空瞬变电磁测量系统测量时飞行高度的要求，吊舱应保持的离地高度为30 m。根据以往完成的航空瞬变电磁测量项目情况，实际飞行测量吊舱离地高度一般可能在25～150 m之间，为了消除因测量距离变化引起电磁响应强度变化的影响，应把测量数据统一换算到30 m高度。按距离的3次方幂指数衰减和指数衰减规律两种方法，计算了几个不同离地高度的衰减系数见表2。从计算结果可以看出两者之间存在很大差异，3次方衰减比指数衰减规律变化要快得多，运用两种方法进行测量数据的高度校正，其结果的差别将会是显著的。

表2 2种衰减规律的衰减系数对比表Table 2 Comparison of attenuation coefficients of two attenuation laws

3 实测数据的校正效果分析

为了比较两种高度校正方法处理后的实际效果,本文以实测的某地支子湖测区航空瞬变电磁项目数据为基础，进行了高度校正及姿态校正后与校正前比较分析。高度校正分别采取3次方衰减和指数衰减规律，姿态校正采用吉林大学殷长春教授等人提出的水平共面装置(HCP)双旋转有无姿态效应时接收机响应之比公式：V(α,β)/V(0,0)=0.5(1+cos2αcos2β)，其中α为摆动角(单位：rad)；β为倾斜角(单位：rad)(曲昕馨等，2014；贲放等，2018)。

该地区水系较发育，浅表以第四系或新近系的洪坡积泥沙地层为主，地层的电阻率较低(电阻率值一般在50～100 Ω·m左右)。测区因靠近县城有高压线路及工厂存在，为了飞行安全，局部测线段的吊舱离地高度达170 m左右，飞机的平均飞行速度基本上在90 km/h左右。以L250线(图3)与L1000线(图4)2条实测曲线为例，对飞行高度起伏不大和起伏较大的两种状况进行分析，比较开展不同高度校正方法前后的效果。

图3 L250线断电时间垂直分量Zoff-dB/dt电磁道堆积剖面数据校正对比图(注：Z4至Z20为不同电磁道的剖面线)Fig.3 Correction comparison chart of vertical component Zoff-dB/dt stack section data of L250 line power outage time (note:Z4 to Z20 are profiles of different electromagnetic channels)a-吊舱离地高度剖面；b-实测电磁道堆积剖面；c-3次方校正电磁道堆积剖面；d-指数校正电磁道堆积剖面a-height profile of pod from ground；b-measured stack profile of electromagnetic channel；c-stack profile of electromagnetic channel after cubic correction；d-stack profiles of electromagnetic channel after exponential correction

图4 L1000线断电时间垂直分量Zoff-dB/dt电磁道堆积剖面数据校正对比图(注：Z4至Z20为不同电磁道的剖面线)Fig.4 Correction comparison of vertical component Zoff-dB/dt stack section data of L1000 line power outage time(note:Z4 to Z20 are the profiles of different electromagnetic channels)a-吊舱离地高度剖面；b-实测电磁道堆积剖面；c-3次方校正电磁道堆积剖面；d-指数校正电磁道堆积剖面a-height profile of pod from ground;b-measured stack section of electromagnetic channel;c-stack profile of electromagnetic channel after cubic correction;d-stack profile of electromagnetic channel after exponential correction

通过该测区L250线和L1000线的断电时间垂直分量Zoff-dB/dt电磁道堆积剖面Z6道数据校正前后对比表3可知，在地表盖层电阻率较低的地区，因为测量吊舱飞行高度的变化，可形成与吊舱离地高度近似镜像关系的干扰异常。采用指数衰减规律的高度校正和姿态校正后，可以基本上消除干扰异常，还原真实的电磁场响应情况，发现地质体引起的航电异常。而采用3次方衰减规律进行校正，放大了距离的衰减效应，电磁道堆积剖面曲线与吊舱离地高度呈现正相关。上述的2种不同高度校正方法的结果相差较大，采用3次方的衰减规律，不但不能消除吊舱飞行高度变化的影响，反而人为扩大了距离衰减的影响，而采用指数衰减规律进行高度校正比较符合实际情况。因此，采用指数衰减规律对整个测区的数据进行校正，来验证这种校正方法的处理效果。

表3 垂直分量Zoff-dB/dt电磁道剖面Z6道数据校正前后对比表Table 3 Comparison of Z6 channel data before and after correction of vertical component Zoff-dB/dt in electromagnetic channel profile

因为避让地物测量吊舱离地高度变化较大，吊舱飞行高度较大线段形成低电磁场区，飞行高度快速下降时接收线圈感应的电磁场变强了，形成飞行高度降低引起的高值干扰异常。对整个测区的测量数据采用指数衰减规律进行高度校正和姿态校正后，能够消除因吊舱飞行高度及姿态变化引起的干扰异常。经高度和姿态校正后电磁场特征出现了明显的变化，原来图5b中没有异常的位置，在图5d出现了D1、D2、D3等3处航电异常，从图5c中可以看出在航电异常D1、D2、D3对应位置飞行高度较大，不进行高度校正就发现不了航电异常。图5d中测区西部近南北向的线性异常带D1应为一条近南北向高压线路引起，东北部的孤立凸起异常D2应为一处工厂引起，东南部的孤立弱小异常D3对应已知的双钩金多金属矿化点。

图5 支子湖测区垂直分量Zoff-dB/dt电磁道(Z6道)数据校正效果图Fig.5 Correction effect of Zoff-dB/dt vertical component electromagnetic channel(Z6 channel) data in Zhizi Lake survey areaa-实测电磁道堆积剖面平面图；b-实测Z6道数据等值线图；c-吊舱离地高度等值线图；d-高度及姿态校正后Z6道数据等值线图a-plan of measured stack section of electromagnetic channel;b-contours of measured Z6 data;c-height contours of pod from ground;d-contours of Z6 data after height and attitude correction

安徽省勘查技术院在该地区开展了钻探工作,据双钩金多金属矿化点ZK5002钻孔资料(图6)，浅部60 m以内是洪坡积泥沙地层，其下是五河岩群片麻岩地层，局部有岩体或岩脉侵入，热液活动明显，埋深70 m以下见含磁铁矿化、黄铁矿化五河岩群片麻岩，在埋深100 m左右视电阻率由200 Ω·m左右降至70 Ω·m以下，视极化率达14%左右，岩心样金含量达到0.4×10-6。这表明通过对测量数据的校正处理能较好地压制飞行高度和姿态变化的影响，凸显出真实的低阻地质异常，航电异常与异常源在位置上有很好的对应性，提高了对异常分析判断的准确性，校正后Z6道数据真实地反应了测区低阻体的分布情况。

图6 双钩金多金属矿化点ZK5002钻孔综合柱状图①Fig.6 Comprehensive column of drillhole ZK5002 from the Shuangou gold polymetallic spot①1-五河岩群；2-侵入岩；3-钻孔1-Wuhe rock group；2-intrusive rock；3-borehole

4 结论

地面瞬变电磁法属于半空间瞬变电磁法，测量过程中低阻围岩的地形起伏对寻找导电矿体异常的影响，目前已经有较深的研究。航空瞬变电磁法属于全空间瞬变电磁法，在我国近年才开展一定数量的生产测量工作，遇到的一些生产技术问题有待我们进一步总结和完善，以达到更好的生产效果。通过三角波场源的理论分析与实测数据校正效果比较，可得出如下结论：

(1)在表层电阻率较低时，飞行测量吊舱离地高低的变化，能引起明显的干扰异常，需要对原始数据进行高度校正处理，通过高度校正能较好地消除因测量高度变化引起的干扰异常，因此建议对航空瞬变电磁法测量数据开展高度校正。

(2)三角波场源航空瞬变电磁法测量的高度校正建议采用近似的指数衰减规律校正，能够达到快速计算实用效果，满足生产数据处理要求。

(3)方波场源航空瞬变电磁法高度校正方法是否适合采用指数衰减规律校正有待进一步研究。

[注 释]

①安徽省勘查技术院.2015.安徽省怀远县双沟地区铁、金多金属矿预查[R].

[附中文参考文献]

贲放,黄威,吴珊,孟庆敏,刘云鹤,廖桂香,西永在.2018.时间域航空电磁系统姿态变化影响研究[J].地球物理学报,61(7):3074-3085.

昌彦君,张桂青.1995.电磁场从频率域转换到时间域的几种算法比较[J].物探化探计算技术,17(3):25-29.

陈斌,陆从德,刘光鼎.2014.基于核主成分分析的时间域航空电磁去噪方法[J].地球物理学报,57(1):295-302.

丁志强,程志平,董浩,李飞.2012.航空电磁法筛选金属矿异常技术研究[J].地质与勘探,48(3):601-610.

杜庆丰,管志宁,何朝明.2006.瞬变电磁数据预处理方法探讨[J].物探与化探,30(1):67-70.

傅良魁.1991.应用地球物理教程[M].北京:地质出版社:168-181.

梁庆华.2012.矿井全空间小线圈瞬变电磁探测技术及应用研究[D].长沙:中南大学:11-18.

梁盛军,张力卡,曹学峰,刘前坤.2014.时间域航空电磁法研究进展综述[J].地质与勘探,50(4):735-740.

李金铭.2005.地电场与电法勘探[M].北京:地质出版社:420-426.

李肃义,林君,阳贵红,田培培,王远,于生宝,嵇艳鞠.2013.电性源时域地空电磁数据小波去噪方法研究[J].地球物理学报,56(9):3145-3152.

刘冲,王宇航,皇键,罗勇.2014.瞬变电磁视时间常数 tau 成像分析与应用研究[J].物探化探计算技术,36(1):28-34.

刘祥平,王建明.2011.改进ICA去噪方法在瞬变电磁信号处理中的应用[J].北京师范大学学报(自然科学版),47(1):35-39.

李永兴.2010.航空瞬变电磁一维正演模拟与反演解释[D].长沙:中南大学:1-68.

罗延钟,张胜业,王卫平.2003.时间域航空电磁法一维正演研究[J].地球物理学报,46(5):719-724.

毛立峰,陈斌,吕东伟.2011.测高数据不准时的直升机航空瞬变电磁一维反演方法理论研究[J].物探与化探,35(3):402-405.

闵刚,王绪本,毛立峰,胡清龙,邱林.2012.磁偶极子源航空瞬变电磁对飞行高度的响特征[J].物探与化探,36(4):591-594.

宁媛丽,周子阳,江民忠,骆燕,彭莉红,朱琳.2020.航空瞬变电磁、航磁在新疆元宝山地区金铜多金属找矿中的应用[J].地质与勘探,56(2):403-410.

牛之琏.2007.时间域电磁法原理[M].长沙:中南大学出版社:7-11.

彭莉红,江民忠,程莎莎,骆燕,宁媛丽,朱琳,2019.航空瞬变电磁法在新疆阿奇山地区铅锌多金属找矿中的应用研究[J].地质与勘探,55(5):1250-1260.

曲昕馨,李桐林,王飞.2014.直升机吊舱姿态变化对电磁场测量的影响规律及其校正方法研究[J].地球物理学报,57(4):1310-1321.

苏朱刘,胡文宝,张翔.2004.电磁资料中的物理去噪法[J].工程地球物理学报,1(2):110-115.

王卫平,王守坦.2003.直升机频率域航空电磁系统在均匀半空间上方的电磁响应特征与探测深度[J].地球学报,24(3):285-288.

殷长春.2018.航空电磁理论与勘查技术[M].北京:科学出版社:73-87.

殷长春,张博,刘云鹤,任秀艳,齐彦福,裴易峰,邱长凯,黄鑫,黄威,缪佳佳,蔡晶.2015.航空电磁勘查技术发展现状及展望[J].地球物理学报,58(8):2637-2653.

岳望.2018.基于核函数的航空瞬变电磁去噪方法研究[D].成都:成都理工大学:5-6.