基于LPV模型的颤振试飞响应预测及激励优化
寇宝智, 雷 鸣, 卢晓东
(中国飞行试验研究院 飞机所,西安 710089)
颤振试飞是一种高风险试飞课目,保障试飞安全和提升试飞效率是工程研究和实施的主要方向。试飞安全监控上普遍采用响应的时域监控和准实时数据处理结合的方法,时域监控主要关注响应的收敛情况,准实时数据处理一般在激励动作结束后,通过遥测数据进行模态参数辨识,获取阻尼变化情况。为了获取良好的响应数据,颤振试飞需要采用有效的激励手段,将线性扫频激励信号通过电传系统施加到操纵面上是目前大部分电传飞机颤振试飞的主要激励手段之一[1]。
雷鸣等[2-3]提出了全机动力学有限元模型为基础的激励响应预测方法,在民机气动伺服弹性和颤振试飞安全监控上得到应用。该方法属于从设计角度出发的正向方法,依赖有限元模型的准确性。频域子空间的方法由Mckelvey等[4-6]提出并进行了各种改进和扩展,这种面向控制的多入多出辨识模型,以其简洁的状态空间模型优势,得到了各种系统建模中的广泛应用,也是基于LPV(linear parameter-varying)模型插值建模的基础,该辨识算法在颤振试飞数据处理中得到了较为成熟的应用[7]。Caigny等[8]提出了局部估计的状态空间模型插值算法(state-space model interpolation of local estimates,SMILE),适用于基于状态空间的变参数系统插值建模。唐炜等[9]从试飞数据出发,基于LPV模型实现了气动弹性鲁棒颤振边界预测,并在风洞试验中进行了验证。Baldelli等[10]基于飞行试验建立了基于LPV模型的颤振预测模型,并通过ATW(aerostructure test wing)进行了飞行试验数据的验证,验证了该建模方法的有效性。Desforges等[11]研究了颤振试飞中扫频信号的优化问题,给出了分段线性扫频相较于传统简单线性扫频的优势。
为了提升实时监控的及时性及试飞数据的信噪比,开发基于局部气动弹性系统模型的响应预测和激励优化方法是一种有效的途径。在颤振试飞速度扩展过程中,通过已飞状态点数据建模,实现关键部位响应的预测,在试飞激励动作实施过程中,将预测响应作为时域数据安全监控的基准,可同时直观考虑响应收敛情况及量值大小。若实际试飞响应偏离预测值太多,则考虑阻尼大的突变,及时实施安全措施,不必等待准实时数据处理结果,提高安全监控的及时性。通过建模仿真,预测模态频带范围,在结构最大响应限制情况下,通过优化激励信号,提升试飞响应数据质量,同时尽量缩减每个激励动作的时间,提高试飞效率。
1 基于试飞数据的局部气弹系统建模
1.1 颤振试飞响应预测及激励优化的流程
建立全局LPV模型来描述某一飞机气动弹性系统,面临依赖参数较多和模型规模太大带来的不确定性等问题。颤振试飞一般采用等高度变速法进行,对于颤振试飞包线扩展,针对在局部试飞状态,选取少量局部关键结构响应,简化为随速压参数改变的局部线性变参数模型,通过不断迭代更新数据,提高准确度及工程可操作性。
颤振试飞响应预测与激励优化随试飞状态推进的流程,如图1所示。从已飞试飞状态点数据出发,通过频域子空间结合最小二乘复频域的两步辨识算法建立各状态点有限阶线性时不变(linear time-invariant,LTI)。然后以速压为变参数进行插值,通过局部估计的状态空间模型插值算法[12],建立随速压变化的LPV模型。最后通过所建模型的仿真进行激励信号优化和响应预测,在试飞实施过程中以预测响应为基准进行安全监控。飞行结束后将新飞状态点数据迭代到模型进行模型更新后接着进行下一点的预测,直到速度扩展结束。
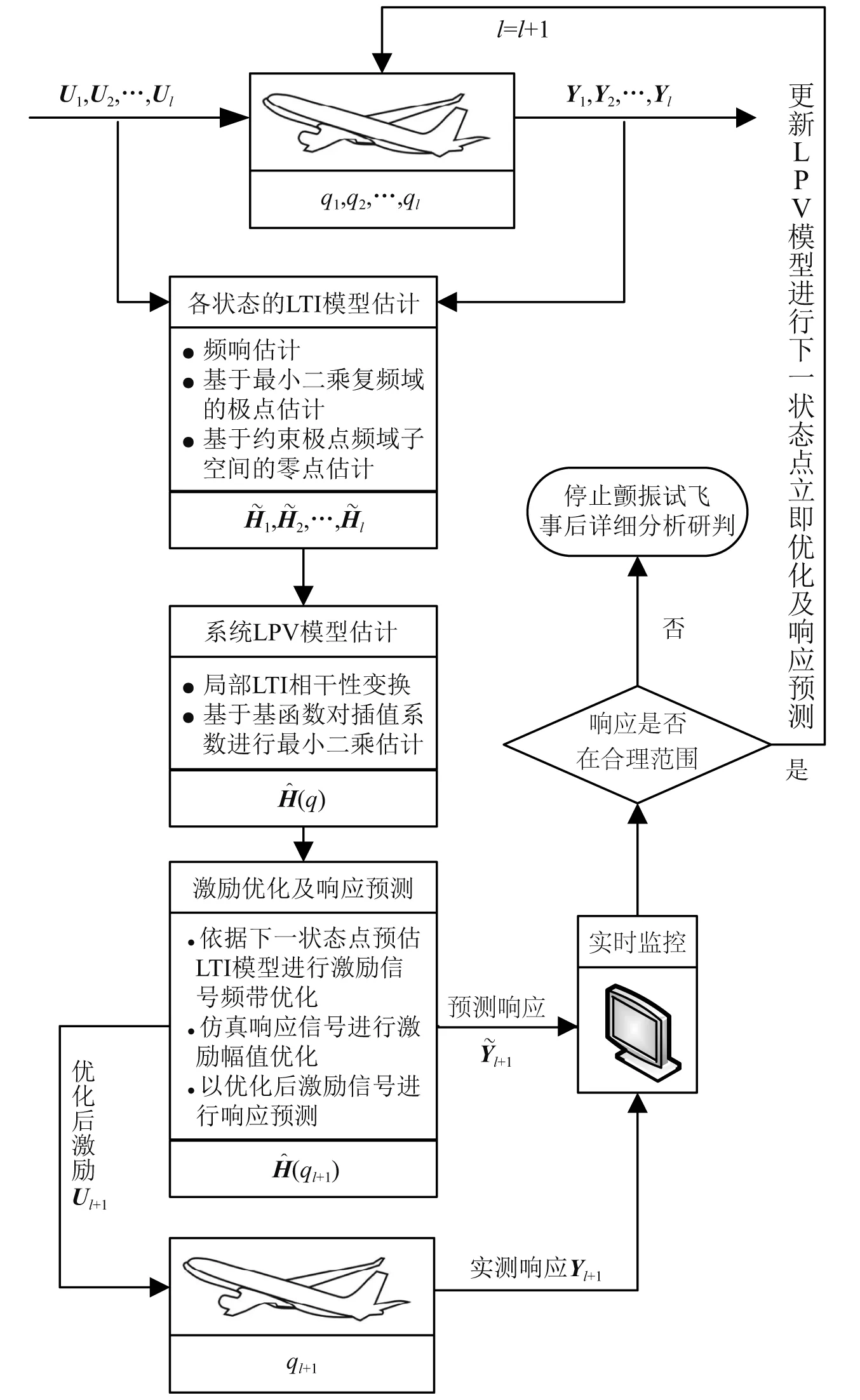
图1 颤振试飞响应预测与激励优化流程图Fig.1 Flowchart of response prediction and excitation optimization for flight flutter test
颤振试飞扫频激励信号一般面临激励时间限制和最大结构响应限制这两个限制,所以激励优化包含两方面:一种是对扫频频率变化率优化;一种是依据响应最大限制值进行激励幅值优化。频段优化一方面为了避免模态遗漏,应覆盖一定的频带范围,同时可根据预测下一状态点的模态频率,采用分段线性扫频进行激励信号优化,在选取的频点范围内增加扫频时间,提高关心频带激励能量和响应的信噪比。颤振试飞中关键部位振动限制值的设置是为了保障安全,避免太大的激励值带来飞机静强度与操纵的问题,所以对激励幅值需要进行一定的限制。
1.2 已飞状态点LTI状态空间模型辨识
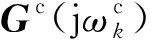
(1)
可等价表示为

H~l=A~lB~lC~lD~l
(2)
假设连续传递函数为Gc(s),双线性变换给出的离散时间传递函数在频域上为
(3)
(4)
以频响函数G(ejωkT)为系统的输出,单位阵为系统的输入,p个输出、m个输入的一个离散时间LTI系统的状态方程表示为
(5)
经过各频点ωk(k=1,2,…,N)处的重复迭代及整合后得到如下形式
G=OrX+ΓrW
(6)
其中,

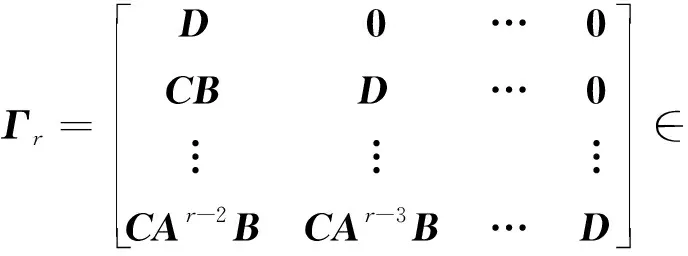
Γr为下三角Toeplitz块矩阵
式(6)的实数矩阵形式为
Gre=OrXre+ΓrWre
(7)
式中:Gre=[Re(G) Im(G)];Wre=[Re(W) Im(W)]; Re为取实部; Im为取虚部。
对矩阵[(Wre)T(Gre)T]进行QR分解
(8)
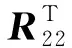
(9)
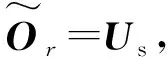
(10)
其中,
J1=[I(r-1)p0(r-1)p×p],
J2=[0(r-1)p×pI(r-1)p],
J3=[Ip0p×(r-1)p]
(11)
(12)
上述子空间方法中,通过奇异值大小确定系统阶次,在气弹系统辨识中,由于有噪声干扰,往往不容易给出清晰的阶次分界。辨识系统的阻尼取值对颤振试飞有重要意义,所以在响应估计中需要兼顾极点的精确性,文献[15]提出结合频域最小二乘法的两步辨识方法,通过LSCF法辨识出极点[16-18],结合上述子空间的零点辨识,提高系统模态参数的精度,有利于进行插值建模时兼顾响应幅值和模态参数预测精度。在待辨识气弹系统结合地面试验和理论计算得出辨识阶次较为明确的情况下,也可以采用其他辨识方法给出系统的极点。

(13)
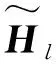
(14)
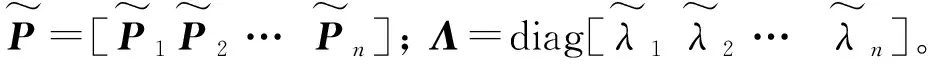

(15)
系统在两步法下的连续时间状态空间估计为

H~l=A~lB~lC~lD~l
(16)
1.3 气弹系统局部LPV模型估计
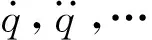

H(q,q·,…)=A(q,q·,…)B(q,q·,…)C(q,q·,…)D(q,q·,…)
(17)
一般颤振试飞是以一系列离散速压为状态点进行,为简化分析,认为保持一定高度和速度范围下的激励响应测试是一个等速压状态,可以只保留式(17)LPV模型的静态响应部分来描述局部变速压气弹系统,即式(17)可简化为

H(q)=A(q)B(q)C(q)D(q)
(18)

(19)

为第l个LTI的观测阵,通过各相干性转换矩阵建立的相干性局部LTI等价模型为

Hl=TlA~lT-1lTlB~lC~lT-1lD~l
(20)

H^(q)=∑Ni=1fi(q)H^i=∑Ni=1 fi(q)A^ifi(q)B^ifi(q)C^ifi(q)D^i
(21)

考虑如下代价函数
(22)

(23)
式中,F(h)为关于h的线性函数,插值建模过程转变为一个线性最小二乘优化问题。
(24)

2 仿真示例
采用Texas A & M University带副翼二元翼段俯仰-沉浮二自由度风洞试验件的线性数值模型进行仿真验证,模型简图如图2所示,具体参数见文献[19-21]。该模型输入为副翼偏度,符合一般颤振试飞舵面激励情况,颤振试飞中响应测量一般为加速度信号,在该翼段前缘处设置加速度计,将原模型的俯仰角及沉浮位移输出转变为前缘法向加速度信号的响应输出。
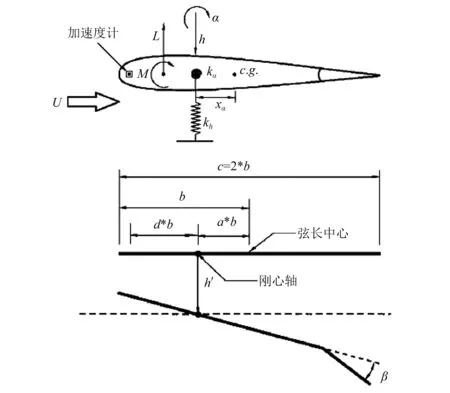
图2 二元翼段模型Fig.2 2DOF wing section model
该二元翼段气动弹性方程为

(25)
式中:M∈2×2为广义质量矩阵;C,K∈2×2为广义阻尼矩阵和广义刚度矩阵,为速压的q的函数;F为输入矩阵;u=β为舵面偏度输入;x=[hα]T为俯仰位移与俯仰角组成的向量;E=[1db]为输出矩阵;y为加速度传感器输出。
将气动弹性方程写成状态空间形式如式(26),理论数值计算颤振速压为89.9 Pa。

x·x··y=0I0-M-1K-M-1CF-EM-1K-EM-1CEFxx·u=H(q)xx·u
(26)
由状态空间方程进行仿真,获取在速压20 Pa,25 Pa,30 Pa,35 Pa下该系统的舵面激励及加速度响应。激励为0~5 Hz,幅值0.1 rad,时间60 s的线性扫频信号,响应信号添加信噪比10 dB的白噪声。
估计以上4个状态点的传递函数,通过频响函数,经两步法辨识获得系统在4个速压点的LTI模型估计。以在速压20 Pa下的情况为例,仿真得到的激励输入与响应输出经滤波后,如图3所示,使用最小二乘法获得系统稳态图,如图4所示,频域子空间和两步法获得的局部LTI估计的频响与原始频响对比,如图5所示。
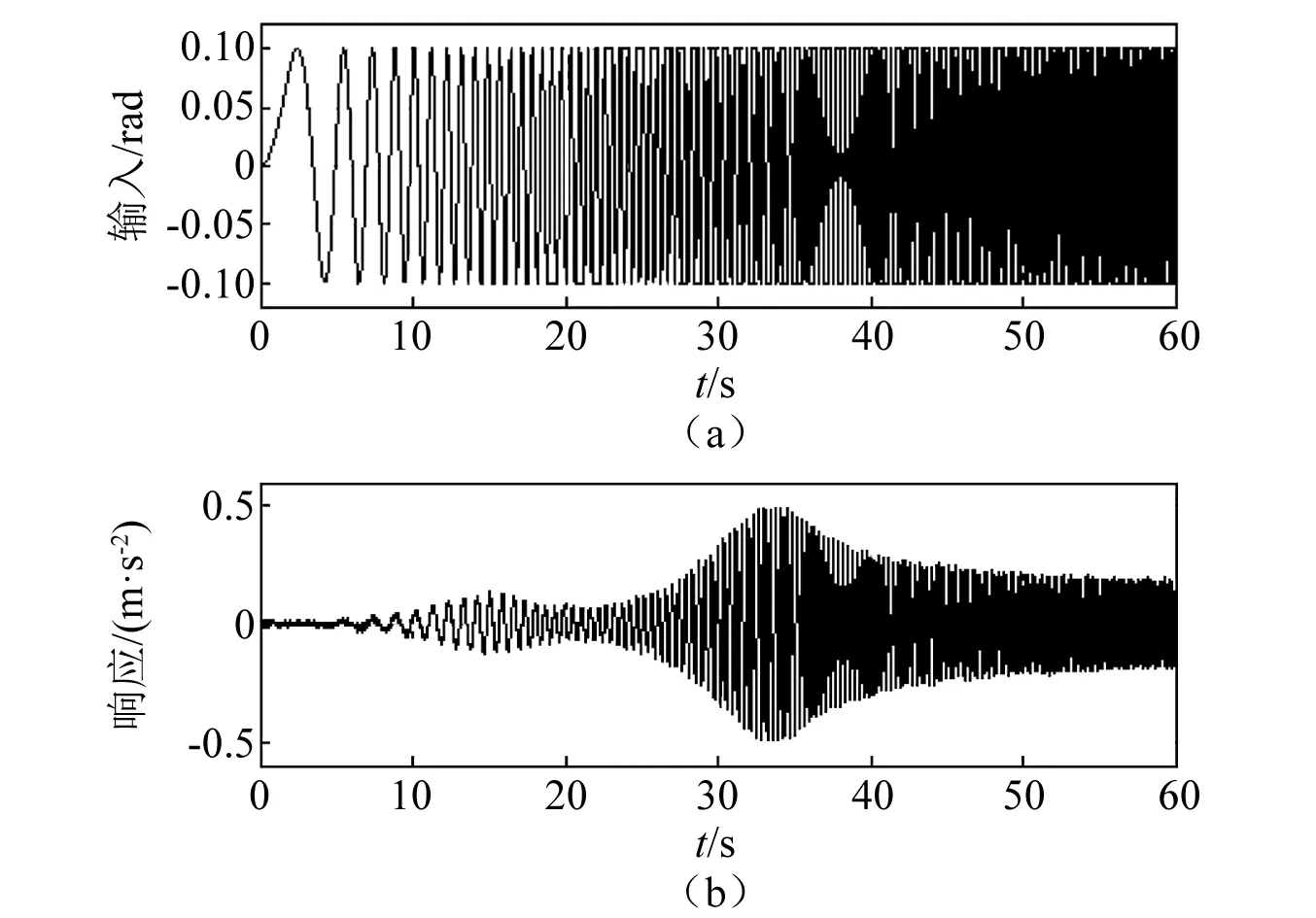
图3 激励输入与响应输出(20 Pa)Fig.3 Excitation and response (20 Pa)
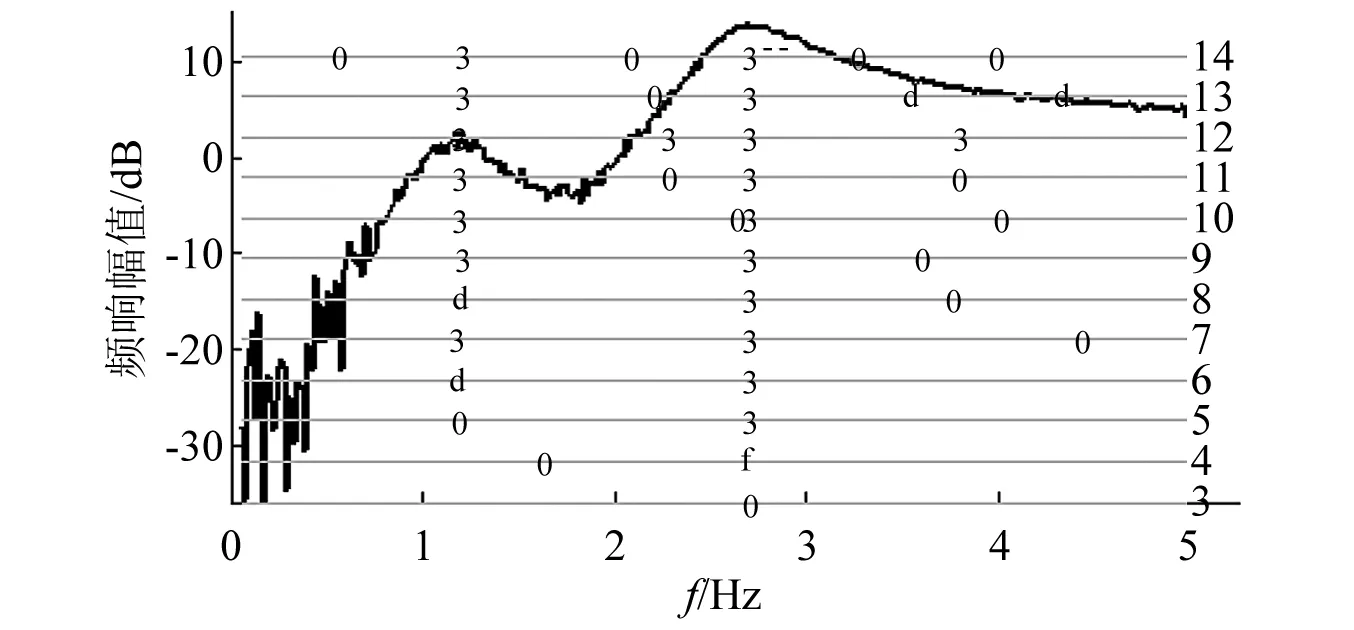
图4 LSCF法获得的系统极点稳态图(20 Pa)Fig.4 Poles stable chart obtained by LSCF method (20 Pa)

图5 辨识LTI模型与原模型频响对比(20 Pa)Fig.5 Comparison of frequency response between identified LTI model and original model (20 Pa)
(27)

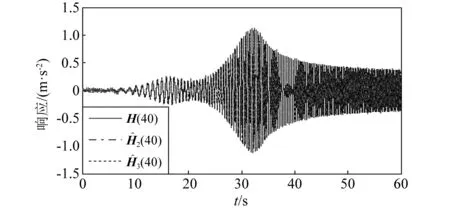
图6 预测响应与原数值模型响应对比(60 s,40 Pa)Fig.6 Comparison of predicted response and original numerical model response (60 s,40 Pa)

图7 预测响应与原数值模型响应对比(10 s,40 Pa)Fig.7 Comparison of predicted response and original numerical model response (10 s,40 Pa)
频带上优化为0~0.8 Hz、扫频5 s,0.8~3.0 Hz、扫频45 s,3.0~5.0 Hz、扫频10 s,的三段线性扫频信号;由于是线性系统,依据上述的仿真响应最大值与激励信号幅值比例,可确定在理想响应值下,激励信号优化后的幅值为0.137 rad。优化后激励信号,如图8所示,使用该信号激励下的系统仿真输出,如图9所示,可见响应最大值为1.5 m/s2,对比图6响应,两个模态频率附近激励时间增多,更有利于事后数据分析。
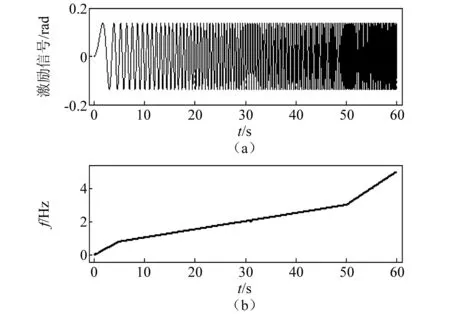
图8 优化后激励信号(40 Pa)Fig.8 Optimized excitation signal (40 Pa)
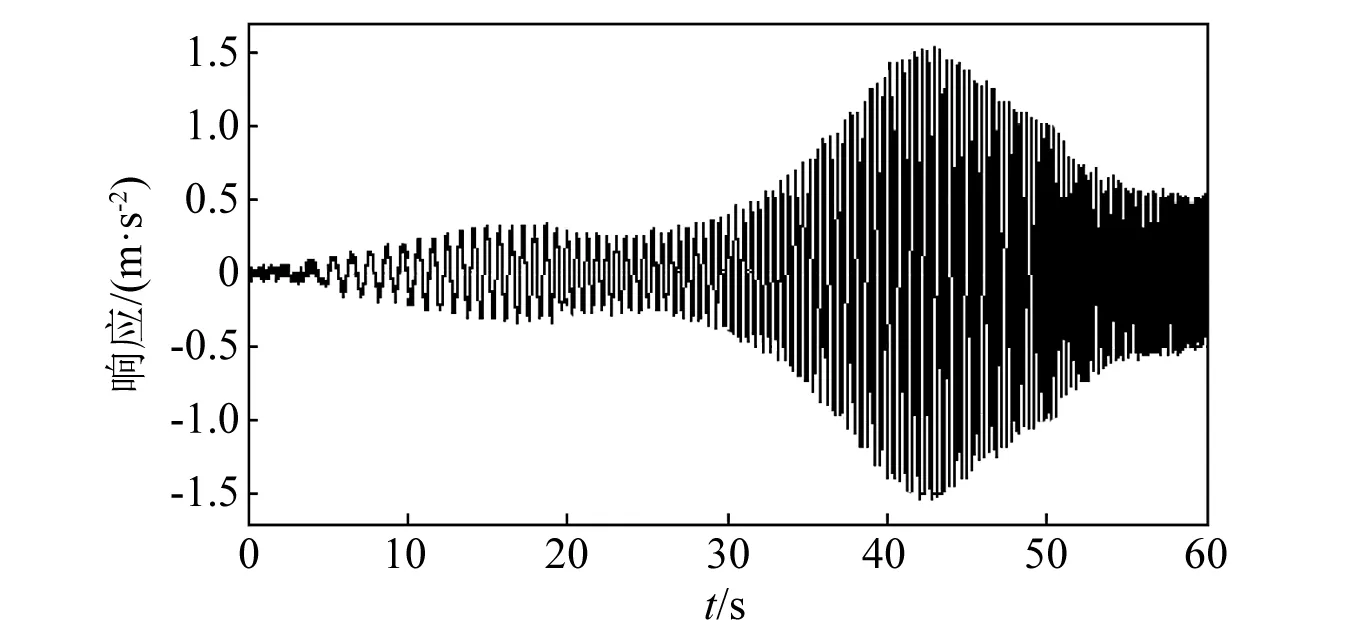
图9 使用优化后激励获得的系统响应(40 Pa)Fig.9 Response using optimized excitation (40 Pa)
根据图1所示流程图,40 Pa后进行速压点扩展,每增加5 Pa为一个速压点,在目标响应值保持1.5 m/s2的情况下基于LPV预测模型优化后激励选取幅值与理论模型计算所需激励幅值对比,如图10所示。
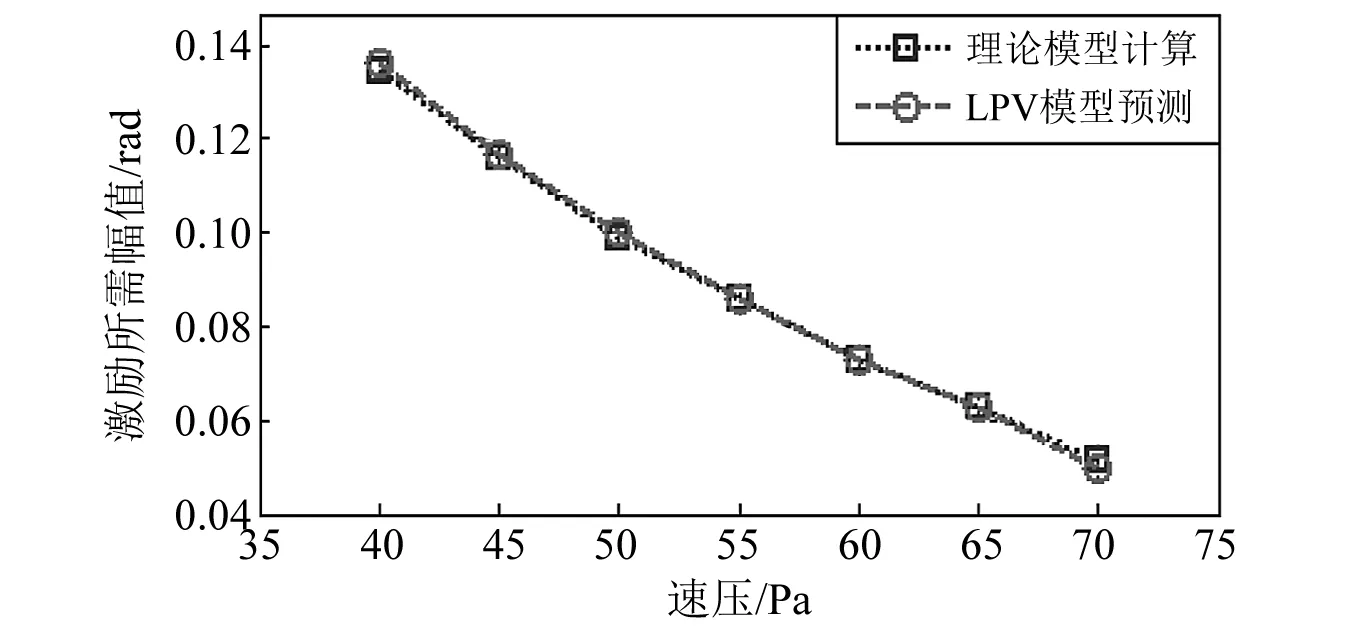
图10 数值模型计算与LPV模型预测所需激励幅值Fig.10 Required excitation amplitudes from calculation of numerical model and prediction of LPV model
速度点扩展过程中,可依据所建LPV模型进行颤振边界预测,辅助判断下一速度点稳定性及余量,随着速度点增加,即用来插值的LTI模型增加,预测精度逐步提高,如图11所示。

图11 颤振速度预测值随插值点数的变化Fig.11 Predicted flutter velocity varying with modeling interpolation points
3 试飞应用
3.1 颤振试飞安全监控
传统的颤振试飞实时安全监控主要关注飞机的飞行状态参数和结构的时域振动响应,在飞机达到要求的飞行状态后,施加几十秒的激励信号,试飞工程师通过遥测数据监控结构响应信号,观察扫频下时域响应的峰值变化情况,结合自身监控经验及该型机前期飞行监控情况做出定性判断,待激励结束后,方可对记录在本地计算机中的遥测数据进行准实时分析,获得关键模态的频率及阻尼。这种实时监控对监控人员的经验要求较高,且在整个试飞周期内会尽可能安排同一工程人员对同一组关键响应进行持续监控,提高对响应变化的敏感性,同时准实时分析对遥测信号的质量要求较高,断点和跳点等均对结果影响较大。使用已飞数据建立的变速压模型进行响应预测,则能够为激励期间的实时安全监控提供一个定量的参考值,通过观察实测各峰值与预测峰值之间的偏差判断目前系统稳定性是否在预算范围内,及时发现阻尼较为迅速的变化趋势,缩短应急中断试验的反应时间。
采用某型机颤振试飞的9个试飞状态点数据,验证本文响应预测模型的工程适用性,状态点飞行高度一致,采用操纵面扫频进行激励。在通过前3个状态点试飞后,开始构建基于变速压模型预测下一状态点激励响应。依据图1所示进行实时安全监控设计,每飞一个状态点,进行模型更新,把下一点的响应预测作为飞行安全监控参考值。
以最后一个试飞状态点为例,速度点VD试飞前,进行机翼尖和垂尾尖部响应预测。首先辨识获得前8个状态点的局部LTI模型,如机翼尖响应在副翼反对称激励下,前8个状态点辨识所得LTI模型的幅频和实测幅频,如图12所示,其中,第5个状态点的辨识LTI模型频响与原频响对比,如图13所示,可见两步法比单子空间法精确度高,有利于后续响应预测准确度。接着通过插值算法获得系统变速压LPV模型,预测第9状态点处的机翼尖部及垂尾尖部响应。最后一个状态点,副翼反对称激励下机翼尖部预测响应与实际试飞响应对比,如图14所示,副翼对称激励下机翼尖部预测响应与实际试飞响应对比,如图15所示,方向舵激励下垂尾尖部预测响应与实际试飞响应对比,如图16所示。对比量值及变化趋势,关键的几个模态在时域响应上的变化均得到较好预测,设计合理的安全系数后,预测响应可满足颤振试飞安全监控要求。
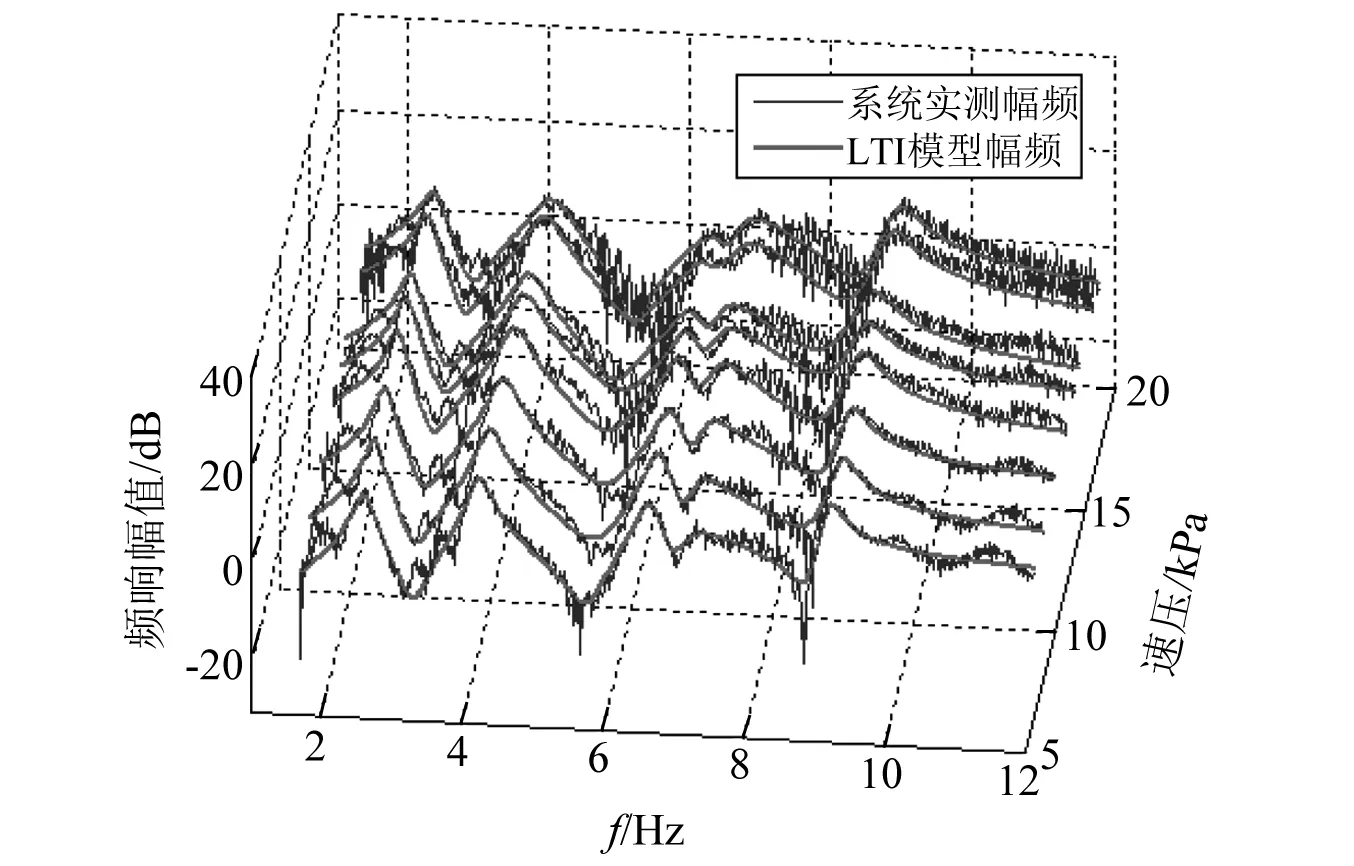
图12 前8个状态点辨识与实测幅频Fig.12 Amplitude frequency responses of identified LTI model and measured system for preceding 8 state points

图13 辨识LTI模型频响与原频响对比图(13.2 kPa)Fig.13 Frequency response of identified LTI model compared with that measured (13.2 kPa)

图14 机翼尖在反对称激励下的预测与实际响应值Fig.14 Predicted and actual acceleration responses at wing tip under anti-symmetric aileron excitation

图15 机翼尖在对称激励下的预测与实际响应值Fig.15 Predicted and actual acceleration responses at wing tip under symmetric aileron excitation

图16 垂尾尖预测与实际响应值Fig.16 Predicted and actual acceleration responses at vertical tail tip
以垂尾响应为例,垂尾尖部响应最大值与预测响应最大值在各状态点下对比,如图17所示。可见预测值准确度随着插值状态点的增加而增加。

图17 真实及预测垂尾响应最大值随速压扩展的变化Fig.17 The real and predicted maximum response values at vertical tail tip varying with the extension of dynamic pressure
基于响应预测可以直观预测下一试飞状态点是否稳定,同时也可以基于已知状态点所建LPV模型进行外推,得到下一状态点的稳定性预估及是否具有足够余量,确保下一状态点安全。该型飞机危险模态为垂尾弯扭耦合,基于变速压模型进行该机垂尾部结构的颤振边界预测。如采用8个已飞状态点数据构建垂尾激励下垂尾响应的局部LPV模型,模型预测的速度-阻尼-频率曲线与各状态点实测值关系,如图18所示,预测速压达到21.3 kPa时,发生垂尾弯扭颤振,扭转阻尼趋于0。第9个试飞状态点速压为18.53 kPa,具有适当余量,可进行该试飞点的试飞。实际试飞中结合边界预测结果通过控制速度增加步长来确保试飞安全。若下一状态点速压比预测边界速压大,为保障试飞安全,则缩短试飞速度步长,使下一试飞状态点速压减小到预测边界速压以下,待试飞后,依据试飞数据更新模型后进行进一步预测分析。试飞中重点关注已知数据建模后预测的下一试飞状态点稳定性及余量,这种基于外插法的边界预测虽然数据点少时不太准确,但随着试飞速度扩展及接近边界,精度逐步提高。

图18 垂尾局部LPV模型频率-阻尼-速压曲线Fig.18 Frequency-damping-dynamic pressure diagram of local LPV model for vertical tail
3.2 激励优化
某型飞机进行颤振试飞,由于飞机油量、性能等限制,无法在高速度状态点下保持足够多激励时间,随着颤振试飞逐步进行,依据已知状态点基于LPV模型建模后,逐步进行激励优化,缩减激励时间,提高响应信噪比。
以副翼激励为例,原始副翼激励设计为幅值0.8°,2~40 Hz,38 s的线性扫频激励,随着飞行速度增加,状态保持时间减少,需要缩减激励时间。依据已飞的几个试飞状态点,预测该响应中包含的3个主要模态下一状态点位于11~24 Hz。在响应不超过4g,保持扫频范围的情况下,依据所建LPV模型仿真后,优化激励信号为幅值0.8°,2~11 Hz、扫频2 s,11~24 Hz,扫频13 s,24~40 Hz、扫频4 s,共计19 s的激励信号。为了验证效果,在下一状态点分别实施原激励信号与优化后激励信号,原激励信号扫频频率随时间变化及机翼翼尖响应,如图19所示,优化后激励信号的分段扫频频率随时间变化及机翼尖响应,如图20所示。可知优化后激励信号在关注的频带范围内仍然保持了1 Hz/s的频率变化率,缩减激励时间则有利于完成更多的激励动作。估算原始激励下机翼尖响应的信噪比为6.13 dB,优化后激励下机翼尖信噪比估算为13.57 dB。图21为本次副翼激励优化前后自谱对比,可见优化后激励提高了关心频带范围内的激励能量。

图19 优化前线性扫频频率变化及机翼尖响应(38 s)Fig.19 Linear sweep frequency and wing tip response before optimization(38 s)
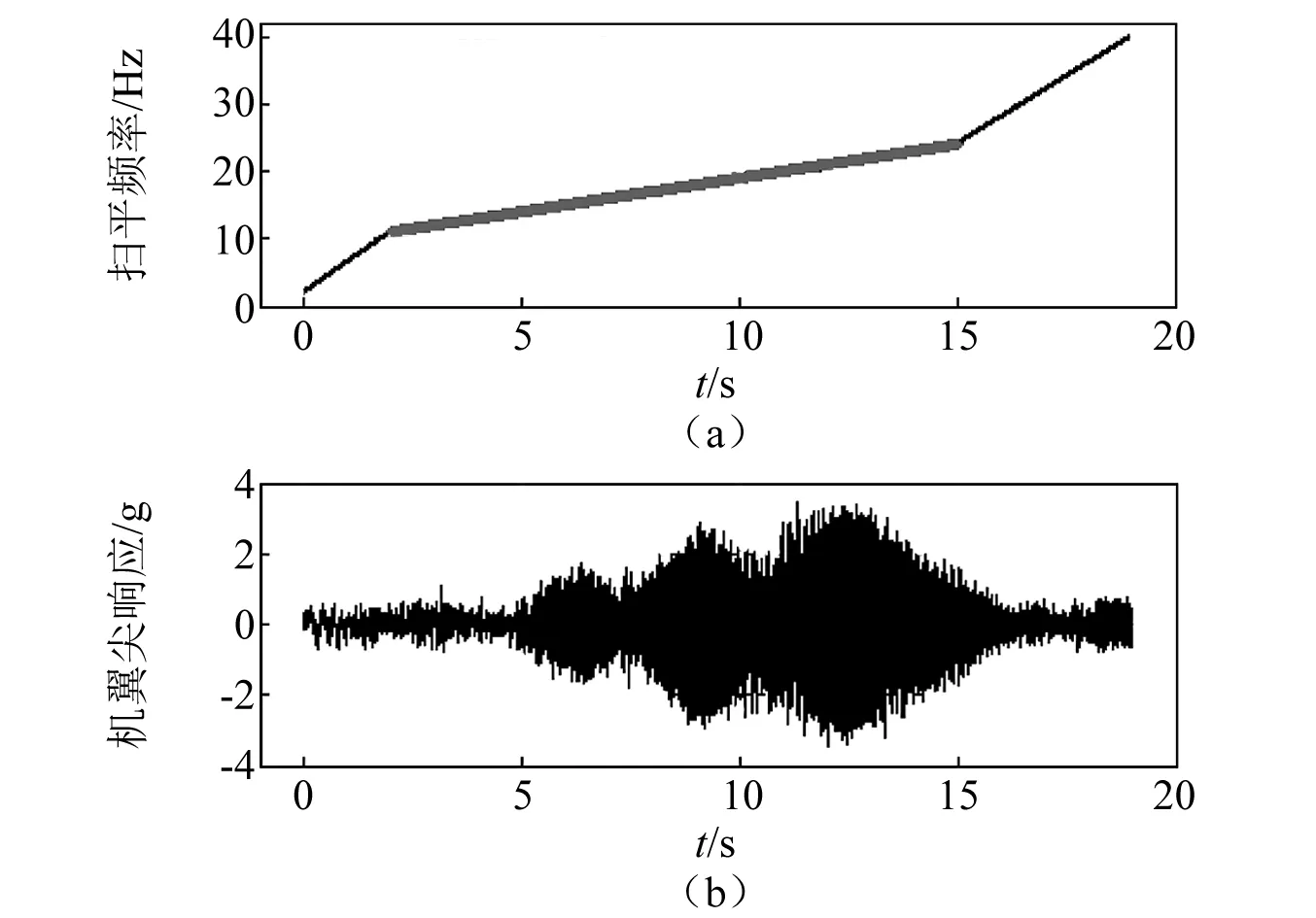
图20 优化后分段线性扫频频率变化及机翼尖响应(19 s)Fig.20 Multi-section linear sweep frequency and wing tip response after optimization(19 s)
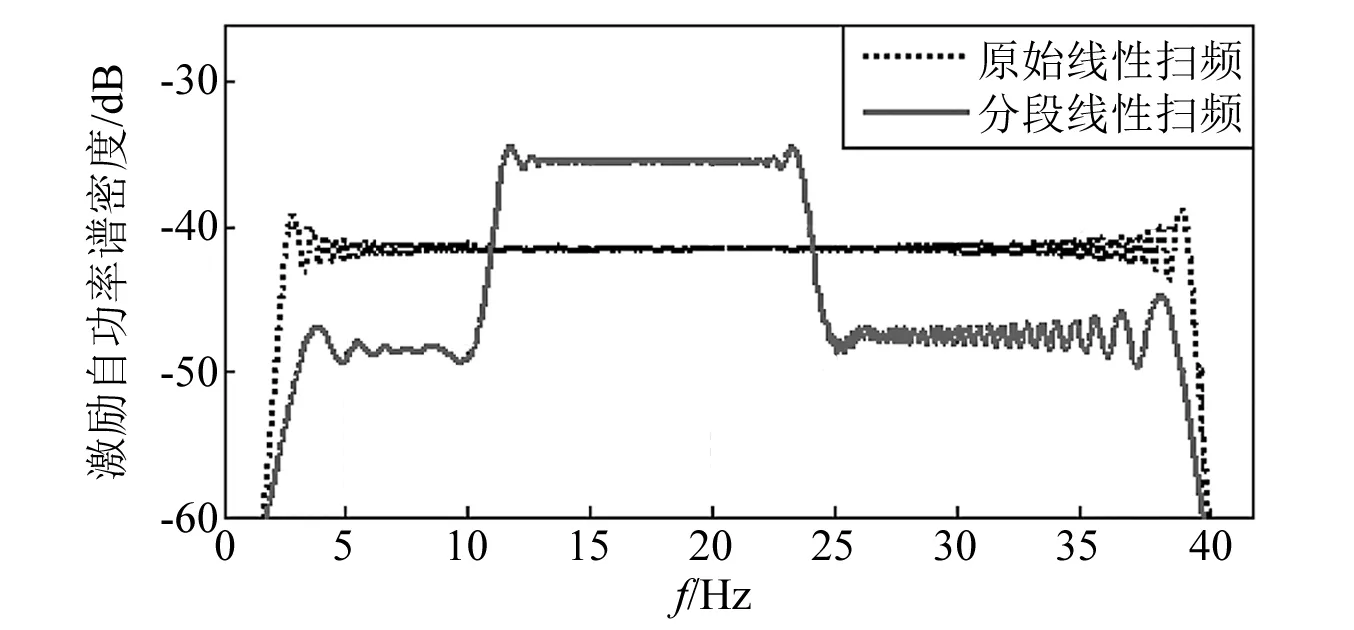
图21 第一次激励信号优化前后激励自谱对比Fig.21 The comparison of PSD of excitation signals before and after the first optimization
继续随着包线扩展接近右边界,速压进一步增大,噪声也进一步增加,且随着数据积累及模型迭代,几个主要关注模态的频率范围进一步稳定,进一步需要优化激励信号为幅值0.8°,5.0~13.5 Hz、扫频4.25 s,13.5~23.5 Hz、扫频15 s,23.5~25.0 Hz、扫频0.75 s,共计20 s的激励信号。整体频带范围进一步缩小,且关心频带范围频率变化率提高到1.5 Hz/s。试飞实施中作为对比组的幅值0.8°,频率范围5.0~25.0 Hz,20 s的简单线性扫频激励下扫频频率变化及机翼尖响应,如图22所示,优化后扫频频率及机翼尖响应,如图23所示,估算的信噪比由8.29 dB提高到10.83 dB。该次副翼激励优化前后自谱对比,如图24所示,关心频带激励能量进一步提高。

图22 优化前线性扫频频率变化及机翼尖响应(20 s)Fig.22 Linear sweep frequency and wing tip response before optimization (20 s)

图23 优化后分段线性扫频频率变化及机翼尖响应(20 s)Fig.23 Multi-section linear sweep frequency and wing tip response after optimization (20 s)
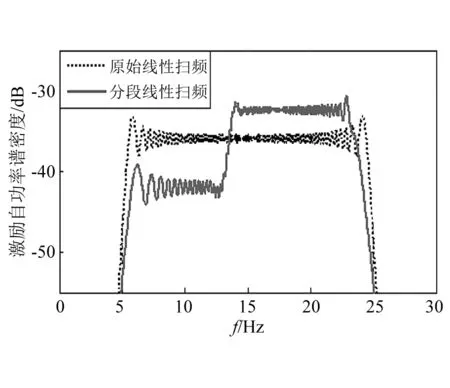
图24 第二次激励信号优化前后自谱对比Fig.24 The comparison of PSD of excitation signals before and after the second optimization
4 结 论
基于LPV模型使用颤振试飞数据进行飞机气弹系统的局部建模,形成了模型预测支撑试飞,试飞数据迭代修正模型的颤振试飞流程,在部分型号飞机的颤振飞行试验中得到较好的应用。随着插值建模的试飞状态点数据增加,预测模型多次迭代后的精度逐步提高,在临近右边界可以提供较为准确的预测值,可有效解决颤振试飞时域监控参考值问题,满足工程安全监控及时性的需求。在激励时间、频带需求和关键部位响应限制情况下,基于预测模型进行仿真计算所优化的激励信号,可有效提升响应数据信噪比,避免激励过程中响应超限,有利于提高试飞效率。
基于状态空间构建动力学模型的方法由于有较为明确的激励和响应数据要求,适用于能够采用操纵面扫频激励得到主要模态的颤振试飞。文中建模方法在亚音速、高亚音速飞机的颤振试飞中得到较好验证,对于马赫数效应明显的超音速飞机的颤振试飞,在实际建模时不能只考虑速压一个变参数,同时需要考虑马赫数和其他可能的影响因素。后续进一步研究适用于超音速颤振试飞的多变参数LPV预测模型,同时研究该方法在气动伺服弹性试飞中的应用。

