基于增秩Kalman滤波的移动车辆荷载在线识别

张超东， 黎剑安， 张 浩

(1. 深圳大学 土木与交通工程学院 城市智慧交通与安全运维研究院，广东 深圳 518060；2. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄 050043)

车辆荷载是在役公路桥梁所承受的主要活荷载之一。移动车辆通过桥梁时，桥梁受到车辆激励产生振动，反过来也对车辆产生激励，两者相互耦合相互影响，被称为车桥耦合振动。近年来，由于组合结构、预应力等新结构形式及高强钢结构和高性能混凝土等新材料的应用，我国公路桥梁的跨度不断增大，向更轻、更柔性的方向发展。加之车辆行车速度提高、载质量增加，公路桥梁因车桥耦合作用而产生的车辆荷载放大效应也不断凸显。在路面粗糙度较差的情况下，车桥耦合作用下的车辆荷载可能是车体自身质量的2～4倍[1]，获取车桥耦合荷载对于车辆超载预警和桥梁结构状态评估具有重要的意义。由于测量手段的限制、测量环境的恶劣以及结构的复杂性等诸多因素，车辆与桥梁之间的相互作用力通常难以直接测量[2]，识别桥梁受到的车辆荷载日益成为桥梁结构健康监测和安全评估的关键。

目前对车辆荷载进行监控的主要手段是桥梁动态称重系统(bridge weigh-in-motion，B-WIM)，其利用压电线圈或桥梁动力响应反演桥面移动车辆等效静荷载。B-WIM已经在实体桥梁上得到了较多应用，但仍然存在一些不足。B-WIM通常基于Moses[3]静态算法，其假设移动荷载将导致桥梁与荷载大小成比例的弯曲，没有考虑车辆与桥梁之间动态耦合效应，因此无法识别移动车辆荷载。

近年来大量考虑桥梁动态特性的移动荷载识别(moving force identification，MFI)方法被提出。此类方法以桥梁上动力响应(加速度、弯矩等)作为已知输入，利用理论分析或有限元计算得到移动荷载与桥梁动力响应的关系，进而将移动荷载识别问题转化为最小二乘求解问题。目前方法主要有两类：时域法[4]和频域法[5]。时域法基于运动方程，通过荷载与响应的卷积积分来确定移动荷载。频域法在频域中求解移动荷载，然后通过傅里叶逆变换确定荷载时程。与频域法相比，时域法拥有更高的精度，适用范围也更广。基于这两类方法，近年来很多移动荷载识别的新方法被提出来了。Liu等[6]基于混合数值方法，应用格林函数和Heaviside阶跃激励的响应函数来确定复合材料表面的线荷载。Chan等[7]基于欧拉梁的运动方程，结合模态叠加法求解移动荷载。

作为一个典型的振动第二逆问题，移动荷载识别是一个典型的不适定性问题，即测量响应含有微小噪音可能引起识别的移动荷载中出现不可接受的偏差。目前该研究的热点在于克服反问题的不适定性，基函数法[8]、正则化方法[9-10]等是最为常用的方法。潘楚东等[11]提出了考虑初始条件的荷载识别方法，该方法利用冗余字典和稀疏正则化方法求解荷载并得到了不错的精度。Asnachinda等[12]基于有限元建模，提出了将更新静态分量的方法应用到连续桥上识别移动荷载。Zhu等[13]提出了基于状态空间法和正则化方法求解移动荷载的方法，但精度容易受到传感器位置的影响。Qiao等[14]利用三次B样条函数和小波分析提出了一种拓展基函数荷载识别算法。Busby等[15]将基于L曲线的正则化方法首次应用在移动荷载识别，开拓了采用正则化方法解决移动荷载识别的研究方向。Zhong等[16]提出了基于L1范数的稀疏正则化的方法，利用试验验证了该方法并取得了不错的精度。

以上所述的移动车辆荷载识别方法仍存在三方面的不足：①基于最小二乘框架下的移动荷载识别通常涉及到系统矩阵伪逆操作，不适定性问题突出，即荷载识别结果很容易受到噪声的扰动而导致结果误差很大甚至发散；②此类方法需使用批量响应序列识别车辆荷载形成超静定方程组，因而无法在线识别荷载；③目前的移动车辆荷载识别方法一般仅建立桥梁结构模型，采用假定车辆荷载动态作用力，未充分考虑车桥耦合振动效应，也无法讨论路面不平度对荷载识别的影响。

为充分考虑车桥耦合作用下的移动荷载识别，需建立车桥耦合振动方程。车桥耦合模型由车辆荷载模型和桥梁模型组成，目前的文献中已有多种桥梁-车辆耦合模型。鉴于三维桥梁模型的复杂性，目前移动荷载研究采用的桥梁模型仍以二维的简支梁桥或连续梁桥模型为主。车辆模型主要包括移动恒载模型、移动简谐荷载模型[17]、移动质量块模型[18]、弹簧质量模型[19]、1/4车辆模型[20]、半车模型[21]以及三维车辆模型[22]。早期的荷载模型相对较简单，并不能较好地反映车辆与桥梁之间相互作用的真实情况。弹簧质量模型、1/4车辆模型和半车模型则能相对较好地反映车辆与桥梁之间的动态效应而且计算量也相对较小；三维车辆模型虽能更完整地反映车辆与桥梁之间的运动状态，但建模过程相对复杂且计算成本较大。

本文基于车桥耦合系统模型，提出基于增秩Kalman滤波的移动车辆荷载在线识别算法。首先建立能考虑路面不平整度的车桥耦合振动方程，计算车辆和桥梁的动力响应以及车桥相互作用力，即车辆荷载。其次，建立桥梁结构的状态空间方程，将移动车辆荷载与状态向量联立构成增秩状态向量。基于增秩Kalman滤波算法，利用少量测点处的桥梁振动响应，实时递归迭代获得增秩状态向量的无偏最小方差估计，实现车辆荷载实时识别。相较于现有的车辆荷载识别算法，本文所提出的基于增秩Kalman滤波算算法具有突出的优势：首先，利用增秩Kalman算法获得移动车辆荷载最佳估计，避免了直接求解反问题带来的不适定性，因此荷载识别精度较高，且结果相对较稳定。其次，增秩Kalman滤波算法能融合多种响应测量值(如加速度和应变)并联合模型预测给出增秩状态向量的最优估计，可同时考虑观测噪声和系统噪声，因此对测量噪音和系统误差有较强的鲁棒性。

1 车桥耦合模型

本文采用的车桥耦合系统模型示意图，如图1所示，其中桥梁模型选用欧拉-伯努利简支梁桥，车辆模型选用拥有一个自由度的弹簧质量模型。图1中：m1和m2分别为车轮质量和弹簧上物体质量；c和k分别为悬挂系统的阻尼系数和刚度系数；z为弹簧质量的竖向位移；ρ为桥梁每延米的质量；EI为桥梁的抗弯刚度；L为桥梁的长度；v为车辆的移动速度；g为重力加速度；桥面在x处的竖向挠度为yb(x,t)，其中x=vt。

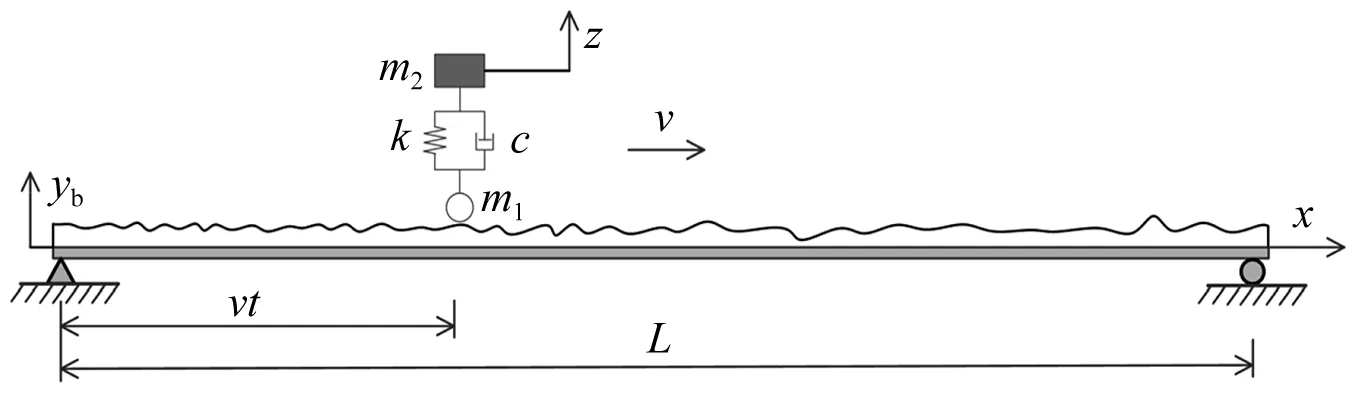
图1 车桥耦合系统Fig.1 Vehicle bridge interaction system

1.1 路面不平度模拟

路面的粗糙度是影响动态效应的重要因素，在ISO 8608：2016标准[23]中，路面不平度被划分为从A级(最好)～H级(最差)8个等级。鉴于桥梁表面的粗糙度相对较好，本文的路面不平度分析仅采用该标准中的前5个等级。路面不平度的表达式为

(1)

(2)

式中：r(x)为路面不平度信号；N为路面离散点的数量；Gk为路面不平度的功率谱密度函数；nk为空间频率；Δn为空间频率的间距，Δn=(nu-nl)/N，一般地，nl=0.011 m-1，nu=2.83 m-1；n0为参考空间频率，一般取0.1 cycles/m；x为桥梁的横坐标；φk为满足(0,2π)的均匀分布数列；G0的取值需要参考路面不平度的等级。

1.2 桥梁运动方程

建立图1中简支梁的有限元模型，其运动方程为

(3)

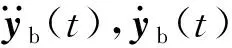
H(t)=[0…Ψ(x0,t) …0]T

(4)

在矩阵H(t)中，移动荷载所作用的单元用形函数Ψ(x0,t)表示，其他单元全用零矩阵代替，从而表示出移动荷载的位置。由于移动车辆的位置在不断变化，所以每一个时间步内都需要对矩阵H(t)进行更新。fint(t)为作用在桥梁上的移动车辆荷载[25]，其表达式如式(5)所示

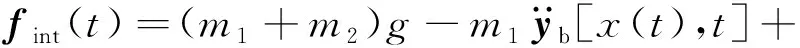
(5)

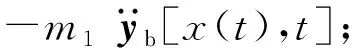
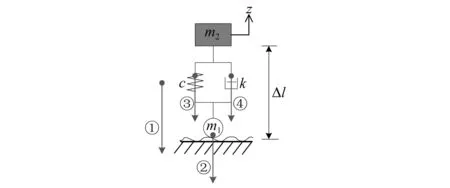
图2 车辆荷载力学模型示意图Fig.2 Schematic diagram of vehicle load mechanics model

yb[x(t),t]=HT(t)yb(t)

(6)

模态叠加技术可大大提高计算复杂系统的效率，桥梁的位移矩阵用模态叠加法可表示为

yb(t)=Φ(t)q(t)

(7)

式中：Φ(t)为桥梁的振型矩阵；q(t)为模态坐标向量。

1.3 车辆运动方程

图1中的车辆模型用运动方程可表示为

(8)

该车辆模型只有一个自由度，故车辆模型不采用模态叠加法。

1.4 车桥耦合振动方程

Zhu等[27]指出车桥耦合方程的解法有两种：一种是在两个的子系统中分别求解车辆方程和桥梁方程；另一种方法是将车辆方程和桥梁方程联立求解。本文采用第2种方法求解，联立式(3)和式(8)得到车桥系统的耦合振动方程如式(9)所示

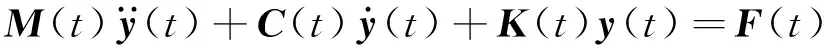
(9)

其中，

利用Newmark-β逐步积分法或者离散状态空间法对式(9)迭代可以求解车桥耦合系统的动态响应，进而可将部分响应作为观测量用于识别移动车辆荷载。

根据式(5)可以计算出车辆荷载的真实值，其可作为标准与识别到的车辆荷载进行比较，以评价识别结果的准确性。本文接下来的第2章将进一步阐述基于AKF算法的移动荷载识别原理。

2 基于AKF的移动车辆荷载识别

2.1 桥梁结构的状态空间方程

根据式(3)建立桥梁结构的状态空间方程为

(10)

其中，

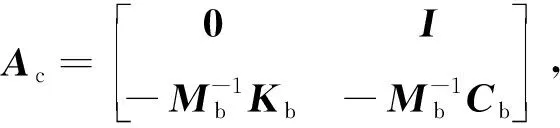
式中，I为单位矩阵。

将式(10)离散化，并施加系统的过程噪声，过程噪声用ωk表示

Xk+1=AdXk+Bdpk+ωk

(11)

其中，

建立系统的测量方程，并施加测量噪声，测量方程的形式为

dk=CdXk+Ddpk+ξk

(12)

式中，Cd和Dd分别为状态空间的观测矩阵和前馈矩阵，可由式(10)构建，用以输出所需的动态响应dk。ξk为观测噪声。桥梁状态空间方程详细的建立过程可参考文献[28]。

2.2 移动车辆荷载识别

利用式(12)求解移动荷载pk的过程中，由于观测值dk并不包含所有节点的动态响应，只能通过部分的观测值求解移动荷载，所以直接求解是困难的。并且由于观测值含有观测噪声以及系统模型的建立含有一定的偏差，求解结果容易因为轻微的干扰而产生很大的误差。AKF利用最优估计的方法求解反问题，求解过程结合观测噪声和模型噪声，其结果不容易因为数据的波动而产生较大误差，适合用于求解移动荷载。

假设荷载pk在第k个时间步的增量为ηk，则荷载pk的递推关系式可表示为

pk+1=pk+ηk

(13)

联立式(11)和式(12)，并将pk作为状态变量增广到状态向量Xk中，得到车桥系统的增秩状态空间方程为

(14)

dk=CaXk+ξk

(15)

其中，

利用AKF算法求解车辆荷载分为两个部分[29]：

(1) 预测部分

(16)

(17)

(2) 更新部分

(18)

(19)

(20)

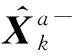
在式(17)和式(18)中

(21)

式中： E 为取数学期望；T为ζk的协方差矩阵，表示系统模型的误差；R为ξk的协方差矩阵，表示观测值的误差。AKF算法通过联合T和R给出状态向量的最优估计：T越小表明模型误差越小，Kalman增益就越信任预估计；反之则越信任观测值。

(22)

图3 基于AKF的车桥耦合荷载识别流程图Fig.3 Flow chart of vehicle-bridge interaction load identification based on AKF

3 车桥耦合系统数值模拟

为验证本文所提方法的可行性，以图1所示的简支梁-弹簧质量组成的车桥耦合模型为例进行数值模拟。车辆的参数如下：m1=3 000 kg，m2=31 700 kg，c=8.6×104N·s/m，k=9.12×106N/m。桥梁的参数如下：L=40 m，EI=2.3×1010N·m2，每延米的质量ρ=5×103kg/m，所有模态的阻尼比均为2%。

将简支梁划分为40个等长度梁单元，建立该桥梁的有限元模型，每个节点仅考虑竖向位移和转角，忽略轴向位移。将高斯白噪声作为测量噪声加入到纯净的仿真响应中，用以模仿包含噪声的测量数据，施加噪声的公式为

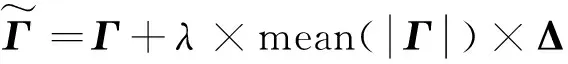
(23)

为评价车辆荷载的识别精度，将识别误差[30]定义为

(24)

式中：ε为识别误差；Ωtrue为桥梁受到的真实荷载，由式(5)计算得出，用作评定识别荷载的标准；Ωid为识别荷载，由AKF算法利用桥梁振动识别得出； ‖·‖2为目标数列的L2范数。

如表1所示，C1～C5为本文讨论到的传感器组合，数量依次递增，传感器的安装位置可参考图4。在图4中，位移传感器和加速度传感器分别安装在桥梁1/4跨、1/2跨和3/4跨处，其中D代表位移传感器；A表示加速度传感器。

表1 传感器组合Tab.1 Sensor combination

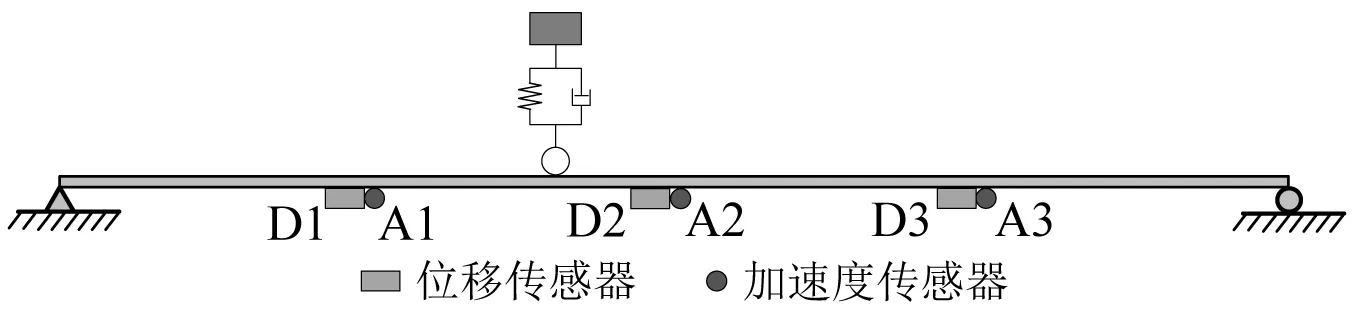
图4 传感器布置示意图Fig.4 Schematic diagram of sensor layout

下文对影响车辆荷载识别精度的各项因素进行了探讨，在未经申明的情况下，默认车速取30 m/s，噪声取5%，路面不平度取A级，采样频率取1 000 Hz，传感器组合取C5组合。

3.1 路面不平度的影响

路面不平度是影响车辆荷载大小的重要指标，也会影响到接触力的识别精度。本文取ISO标准路面不平度的前5个等级(即A～E级)作为路面不平度讨论因素。

图5为各等级路面不平度下，车辆荷载与静载(车体自质量)的比值的箱线图，其中“S”表示完全光滑的路面类型。从图5中可以看出，在各等级的路面不平度下，荷载比值的中位数基本上维持在1处，这是因为车辆是围绕静载波动的，中位数也就与静载相接近。随着路况变差，路面不平度增大，移动车辆荷载的分布范围变大，波动更为剧烈。表明移动车辆动态效应越显著，车辆与桥梁之间的车辆荷载就越大。而箱线图中的最大值则更直观地表现了车辆荷载与静载的关系，如E级路面下，车辆荷载的最大值达到了静载的4倍，这表明桥梁受到的车辆荷载是不容忽视的。可以说，路面不平度越差，桥梁受到的车辆荷载就越大，进而使桥梁更容易受到损伤,这也体现了识别车桥耦合车辆荷载对于桥梁健康监测的重要性。

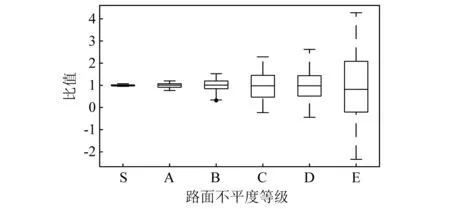
图5 各等级路面下车辆荷载与静载比值箱线图Fig.5 Box plot of the ratio of dynamic load to vehicle weight for each road surface level

图6为A级路面不平度条件下车辆荷载的识别结果，识别误差为1.32%。图7为E级路面不平度条件下车辆荷载的识别结果，识别误差为5.26%。相比于图6，图7的误差虽然有所增加，但仍然处于较低的水平。值得注意的是，图7中的车辆荷载明显大于图6中的车辆荷载，这进一步说明路面粗糙度会明显影响到车辆荷载的大小。

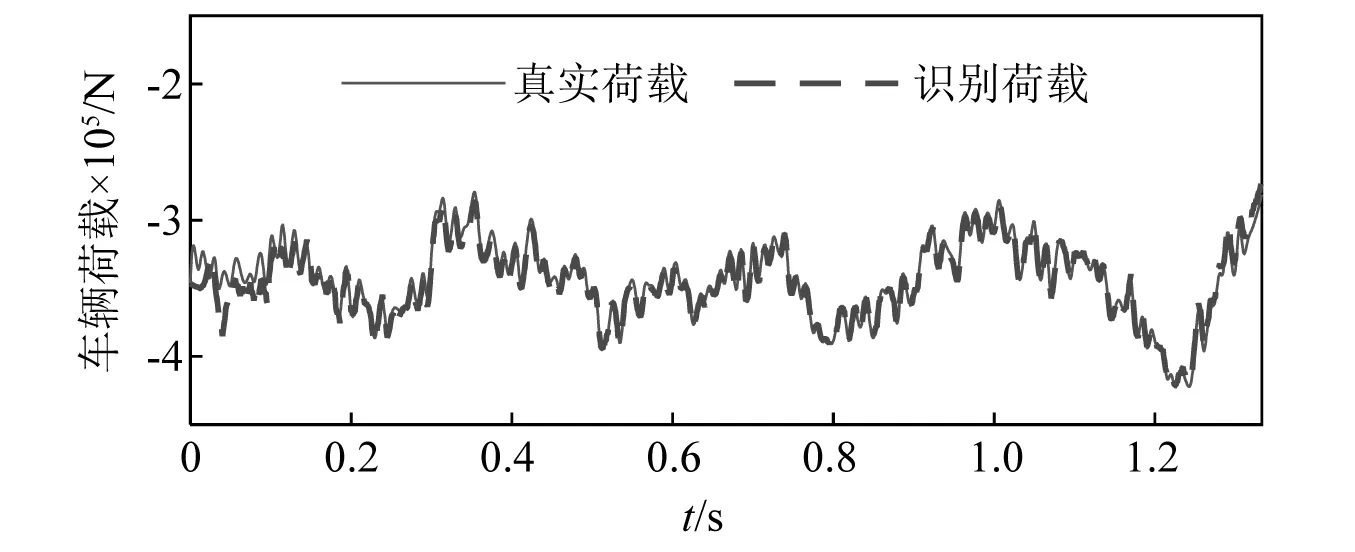
图6 A级路面不平度的车辆荷载识别图Fig.6 Identification diagram of vehicle load for A level pavement

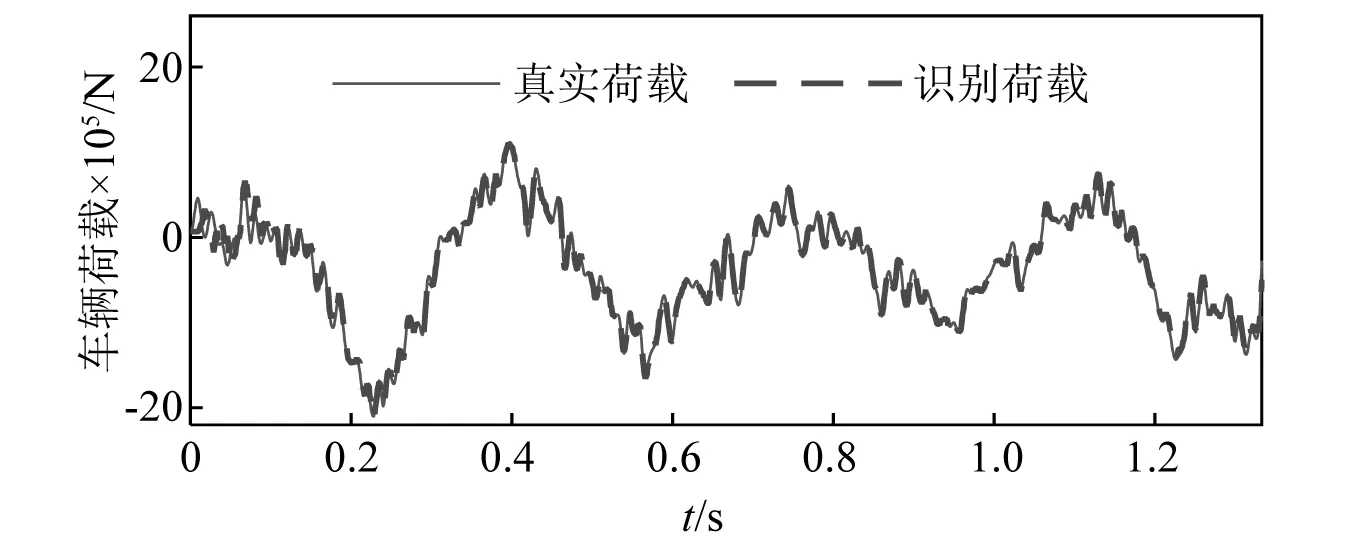
图7 E级路面不平度的车辆荷载识别结果Fig.7 Identification diagram of vehicle load for E level pavement

图8为不同路面粗糙度下车辆荷载的识别误差曲线，随着路面粗糙度变差，车辆荷载的识别误差也越来越大，但是增量并不明显，在最不利的路面下误差仅有5.26%，这样的增幅是可接受的。由于桥梁表面的不平整度一般不会太差，故无需考虑E级路面之后的荷载识别情况了。

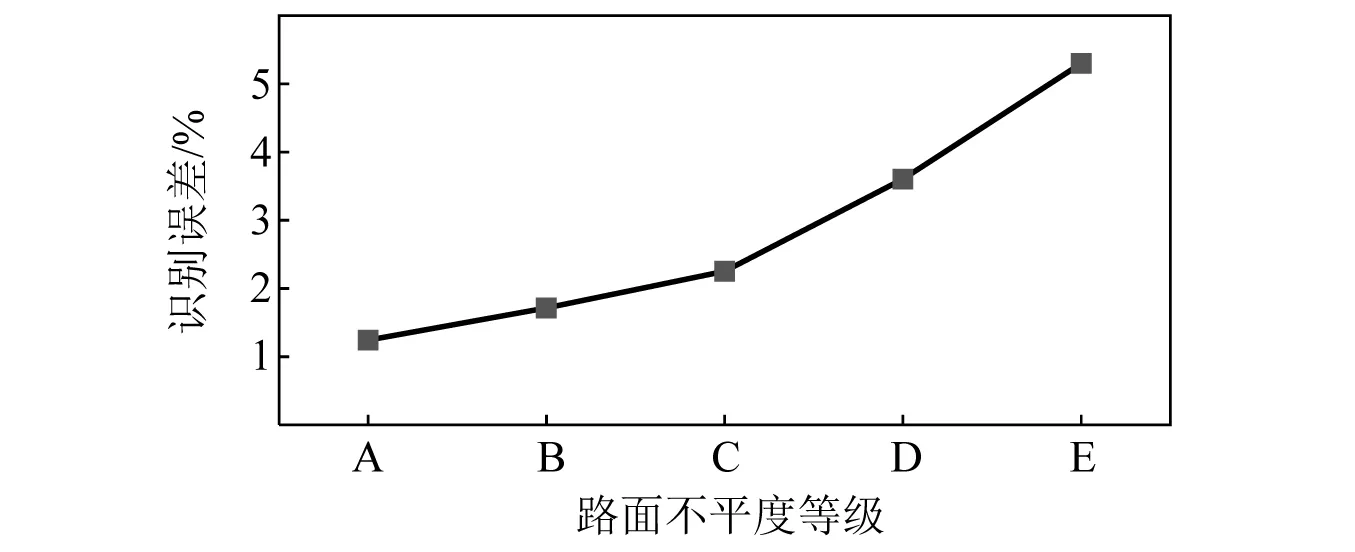
图8 不同路面不平度下车辆荷载的识别误差Fig.8 Identification error of vehicle load under different road roughness

3.2 车速的影响

图9展示了车辆在A级不平度的路面上，车速处于10～100 m/s时识别误差的变化曲线。可以看出，车速的变化对识别精度的干扰很小，误差值虽然呈缓慢上升的趋势，但上升幅度非常小，即使在100 m/s的车速下，识别误差依然能保持在3%以内。需要说明的是普通汽车的速度一般在40 m/s以下，此时误差值在2%以内，这说明所提方法的识别结果对车速不敏感。

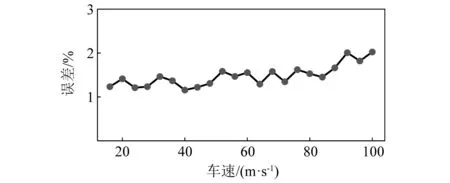
图9 不同车速下车辆荷载识别误差Fig.9 Identification error of vehicle load at different speeds

3.3 噪声的影响

图10～图12分别展示了噪声在2%，15%和40%时的荷载识别结果，误差分别是1.12%，1.78%和3.29%。从图中可以看出，三种情况下荷载识别精度都相对较高。如图12所示，即使是在40%噪声的干扰下，识别荷载与真实荷载依然达到了相对较高的重叠程度，但在桥梁两端处，荷载的识别精度较差。这一现象在文献[31]中也有见到。

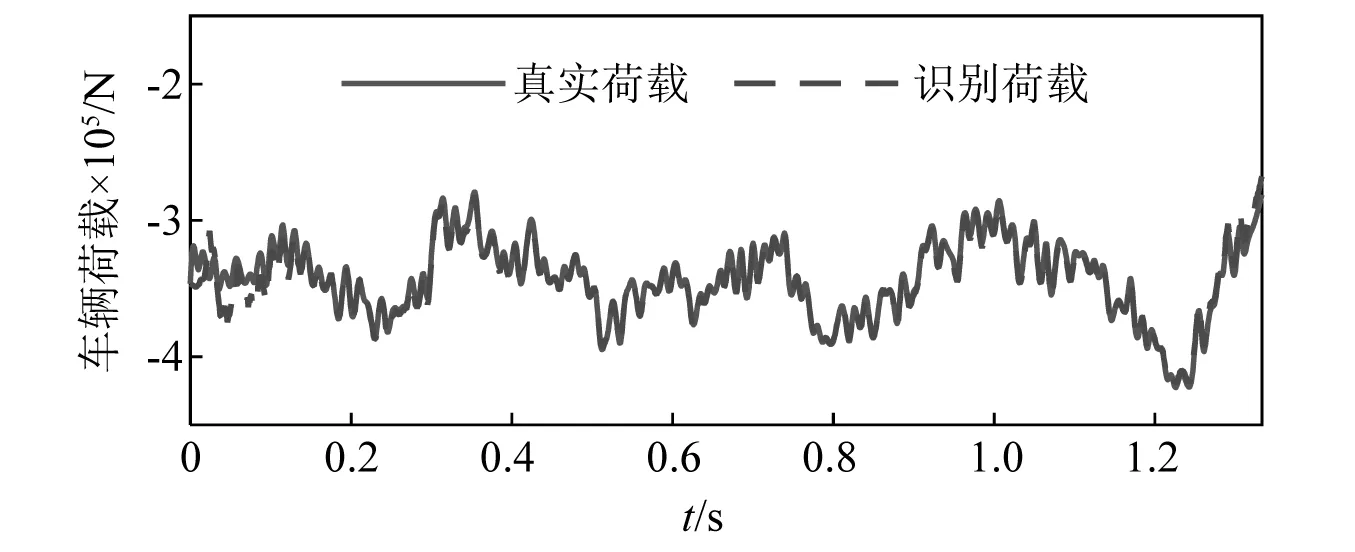
图10 噪声为2%时车辆荷载识别误差Fig.10 Identification error of vehicle load at (2% noise)

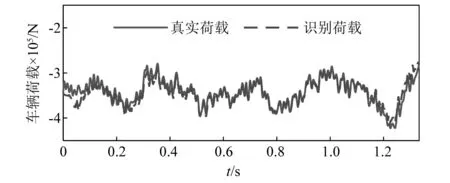
图11 噪声为15%时车辆荷载识别误差Fig.11 Identification error of vehicle load at (15% noise)

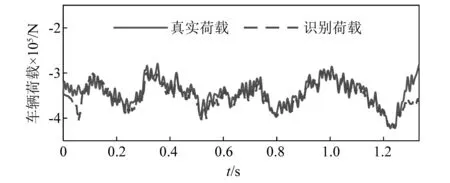
图12 噪声为40%时车辆荷载识别误差Fig.12 Identification error of vehicle load (40% noise)

需要指出的是：多数文献的数值算例中，引入的噪声比例不会超过15%。本文最多考虑了40%噪声，强大的处理噪声的能力是所提方法区别于其他现有方法的优势。

图13展示了噪声从2%～40%的误差曲线，随着噪声的增加，误差曲线呈缓慢上升的趋势。即使是在40%的噪声条件下，识别误差依然能保持在3%左右，可以说本文提出的方法具有强大的抵抗噪声干扰的能力。这是因为AKF算法联合系统估计误差和观测误差，将最优估计的理论误差降到最小，以此达到过滤噪声的目的。

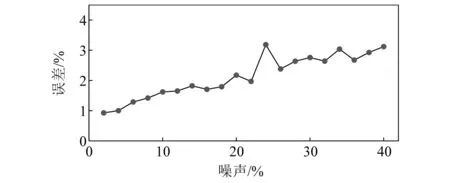
图13 不同噪声下的车辆荷载识别误差Fig.13 Identification error of vehicle load under different noises

3.4 传感器配置的影响

很多论文都将传感器的数量纳入影响荷载识别精度的指标，传感器数量越多，采集到的数据就越完善，计算的结果也就越接近真实值。但是传感器是昂贵的，其数量越多经济成本就越大，所以用尽量少的传感器进行结构健康监测日益成为学者们研究的方向。本文讨论了表1所示的5组传感器组合、最多6个传感器对荷载识别精度的影响。

图14展示了C1组合下，车辆荷载的识别结果，可以看出误差主要集中在桥梁两端，而荷载处于中间时误差较小。图15展示了5种组合传感器组合的识别误差。传感器数量最少的C1组合识别误差是最大的，误差值为5.93%，依然处于比较小的误差水平。图15中各工况下的误差值均处于7%以内，这说明了本文所提的方法能用较少的传感器完成车辆荷载的识别，但采用的传感器数量越少，荷载识别误差也越大。

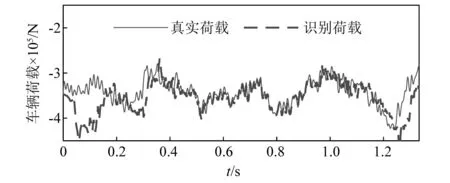
图14 C1组合下车辆荷载识别结果Fig.14 Identification result of vehicle load (case: C1)

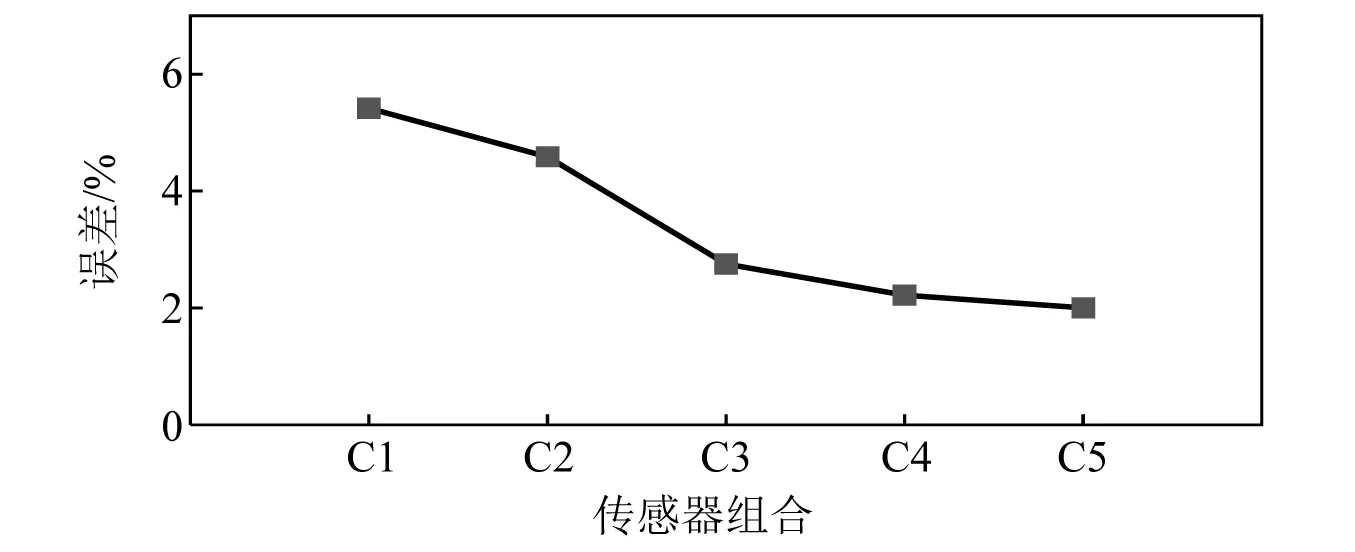
图15 各传感器组合下车辆荷载识别误差Fig.15 Identification error of vehicle load under each sensor case

3.5 采样频率的影响

采样频率是影响荷载识别精度的重要指标，当采样频率只有100 Hz的时候，所提方法在默认工况下识别车辆荷载的误差在8%左右，依然处于相对较低的误差水平。如图16所示，提高采样频率能明显改善荷载识别精度，当采样频率达到1 000 Hz的时候，识别精度的提升则显得相对微弱了。这说明过低的采样频率会影响到所提方法的准确性，但采样频率达到200 Hz或以上时，荷载识别精度相对可靠。

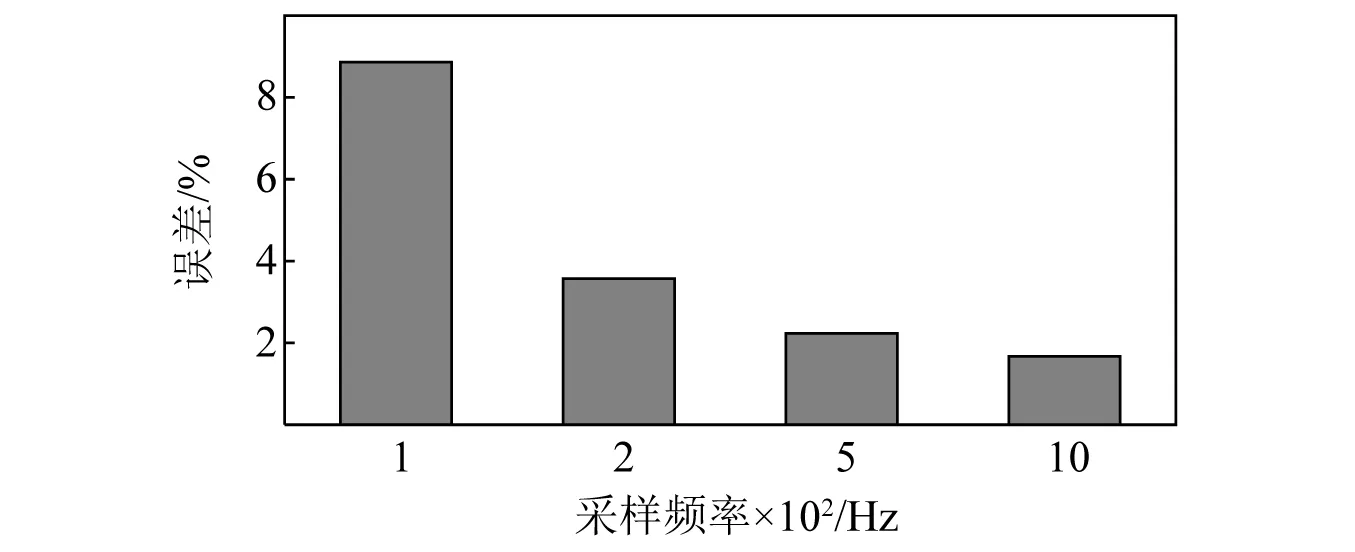
图16 各采样频率的误差对比Fig.16 Error comparison of each sampling frequency

3.6 与现有方法对比

基于车桥耦合的移动车辆荷载识别的相关文献比较有限，本节将本文所提的方法与模型相近的文献[32]相对比。文献所提的方法(加权L1范数正则化方法，W-L1R)精度较高，具有一定的参考性。

两者的仿真模型的主要区别在于：①Pan等采用的是模拟的带有冲击效果的简谐荷载，而本文采用的是基于弹簧质量模型的车桥耦合荷载，更能反映车辆与桥梁之间的实际作用；②Pan等没有考虑桥面的不平顺，本文考虑了桥面不平顺且发现桥面不平顺对荷载的识别精度是有影响的。

表2为参考Pan等研究中的各方法识别荷载的误差对比结果。统一用桥梁的跨中加速度响应和1/4跨处弯矩响应来识别移动车辆荷载。由表2可知， W-L1R方法识别车辆荷载精度稍好于本文做提的基于 AKF的方法；而AKF的方法明显好于L1范数正则化和Tikhonov正则化移动荷载识别方法。

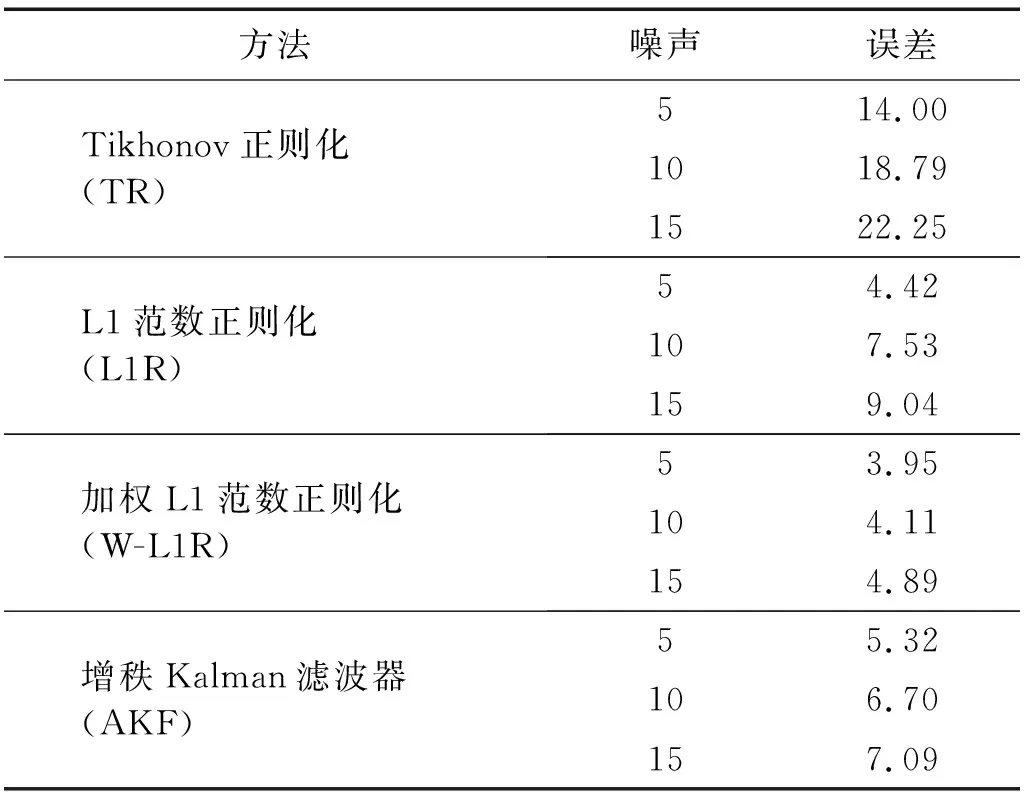
表2 各方法的识别误差对比Tab.2 Error comparison of methods %

表3为不同测点下，本文所提方法(AKF)和Pan等所提方法(W-L1R)的误差对比，其中1/4m表示1/4跨弯矩测点，1/2a表示跨中加速度测点。当测点仅选用1/4m的时候，W-L1R方法识别车辆荷载精度稍好于基于AKF的方法，而当测点选用1/2a的时候，基于AKF的方法识别车辆荷载精度稍好于W-L1R方法。

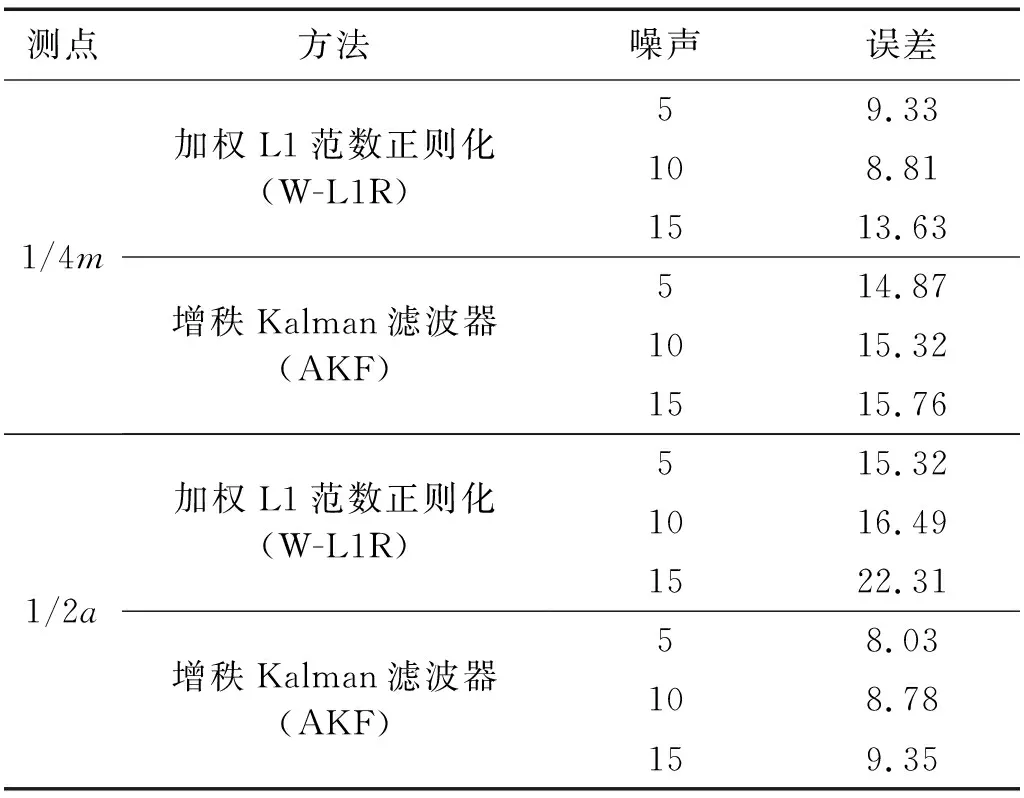
表3 不同测点的识别误差对比Tab.3 Error comparison of different measurements %

综上所述，传感器的种类和位置对不同方法识别移动车辆荷载影响不同。仅从误差上看，本文所提的基于AKF算法识别移动车辆荷载与W-L1R识别精度相当，都优于L1范数正则化和Tikhonov正则化车辆荷载识别算法。但是需要指出的是，基于本文所用的荷载模型考虑了桥面不平整度，同时所提的算法是一种递归算法可以实现车辆荷载在线识别。

4 结 论

为验所提方法的可行性和准确性，本文基于由简支梁桥-弹簧质量模型构成的车桥耦合系统，详细讨论了路面粗糙程度、车速、噪声、传感器配置和采样频率对车辆荷载识别误差的影响，列出了详细的工况并与现有方法进行对比，得出以下结论：

(1) 基于AKF的移动荷载识别方法能利用较少数量的传感器获得的桥梁动态响应有效地识别移动车辆与桥梁之间的接触力。

(2) 所提方法对车速和噪声不敏感。随着噪声的增加，所提方法的识别误差小幅增加，当噪声为40%时，识别误差仅为3%左右。所提方法受车速影响也不明显，随着车速的增加，所提方法的识别误差缓慢增加，最高仅为2%左右。

(3) 传感器的配置和采样频率是重要的影响因素。当所用到的传感器数量过少或者采样频率太低时，所提方法的识别精度较低。

(4) 较差的路面不平度不但会明显增大车桥相互作用力，而且会降低基于AKF的车辆荷载识别的精度。但数值结果表明，在路面状况较差的情况下，所提的方法识别车辆荷载仍较小(E级路面荷载识别误差为5.26%)。

(5) 所提的方法采用逐步迭代的方法识别车辆荷载，无需提前获取结构的全时程响应，为车辆荷载的实时识别提供新的方法。

(6) 仿真结果显示，在荷载进入桥梁时，荷载未能得到良好的识别效果，这是该方法较为明显的不足，也是我们接下来的研究方向。