过流条件下泵站管道振动响应混沌特性分析

张建伟， 张翌娜， 程梦然， 王立彬

(1.华北水利水电大学 水利学院，郑州 450046； 2.黄河水利职业技术学院，河南 开封 475004)

泵站管道长期运行过程中，易受自然及人为因素的影响而导致产生不同程度的振动[1]，长时间、无规律的管道振动会导致管系及其附属系统结构产生松动，严重时会造成灾难性的破坏[2]，因此，分析泵站管道的振动特性以避免其不利振动具有重要的研究价值。

混沌是强非线性结构在振动中表现出来的一种独特的力学现象，大多学者认为输液管道振动属于弱非线性，主要集中于对水流等激振源所产生的混沌现象的研究。在非线性问题的研究上，对管道本身存在的混沌现象研究较为匮乏。研究发现输液管道的混沌现象并不仅仅取决于结构非线性的强弱，对某些结构，即使是弱非线性或是线性结构，也会出现混沌运动[3]。PaïDoussis等[4]研究了在非线性运动约束及定常内流作用下悬臂输流管道的动力学问题，发现了该系统下的混沌运动。Tang等[5]以增加非线性力的方式得到输流管道的混沌特性，发现混沌的出现与否受管道内流速影响最大。Sinir[6]研究了匀速输流微曲管道的非线性振动问题，并在其横向振动中观察到周期性和混沌运动。Zhao等[7]分析了热荷载作用下水流脉动激励产生的管道振动中的混沌现象，得到频率响应与水流脉动速度之间的关系。

管道系统混沌特性的研究大多基于油气压力管道及特定非线性约束条件的输流管道数学模型，而对泵站管道系统的混沌特性分析较少，且以往研究成果中大部分仅对振动系统的混沌特性进行分析，并未进一步探究使其产生混沌特性的振动激励源。本文以某灌区泵站管道工程实测振动响应为研究对象，利用饱和关联维数、最大Lyapunov指数等混沌特性定量判别指标，分析不同工况下泵站管道各测点振动响应的混沌特性；采用改进的变分模态分解(improved variatronal mode decomposition, IVMD)方法分析典型工况下测点振动响应序列，研究各个本征模函数(intrinsic mode function, IMF)成分及混沌特性，从而得到引起泵站管道产生混沌特性的振动激励源。

1 基本理论

1.1 混沌特性识别方法

目前，混沌特性识别方法大致分为定性分析方法和定量分析方法。其中定性分析包括相轨直接观察法、Poincare截面法、功率谱分析法等，具有简单易行的特点，但仅限于判定系统是否具有混沌特性，无法实现不同工况下的横向比较；定量分析方法如应用广泛的饱和关联维数法、最大Lyapunov指数法等可以通过对参数值大小的比较，反应不同条件下响应振动复杂性及混沌特性的强弱[8]。为了提高结论的可靠性，本文同时选取饱和关联维数法、最大Lyapunov指数法作为泵站管道振动响应混沌特性识别指标。

1.1.1 饱和关联维数法

关联维表征动力系统的紧凑程度，用以体现系统的复杂程度，当某一系统饱和关联维数存在时，即可判定其具有混沌特征[9]。对于一个m维相空间，其关联函数C(r)定义为

(1)

式中：C(r)为关联函数；r为任一正常数；M为相点个数；‖Yi-Yj‖为相空间内i,j两点间的距离；H(t)为Heaviside函数，定义为

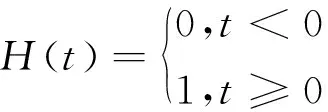
当时间序列具有混沌特征时，对于正值r，关联函数C(r)与r的关系为

C(r)∝αrD2

(2)

式中：α为常数；D2为关联维数，可以通过log2C(r)～log2r图的斜率求得，即

(3)

1.1.2 最大Lyapunov 指数法

Lyapunov指数是根据相轨迹有无扩散运动特征来判别系统的混沌特性。一般地，正的Lyapunov指数代表的方向对吸引子起支撑作用；而负的Lyapunov指数对应的收缩方向，在抵消膨方向的作用后，贡献吸引子维数的分数部分，故正Lyapunov指数是混沌的一个显著特征。设某一系统最大Lyapunov指数为λ1，则λ1取值为正即可判定系统存在混沌成分，其值大小反映混沌程度的强弱。

Rosenstein等[10]提出了一种计算λ1的小数据量法，其基本步骤如下：

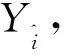
(4)

式中，p为时间序列的平均周期。

定义该邻点对j个离散时间步之后的距离为

(5)

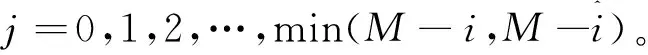
对每个j，求出所有i的lndi(j)平均

(6)

式中,q为非零lndi(j)的数目，采用最小二乘法做出回归直线，则该直线斜率即λ1。

1.2 改进的变分模态分解

VMD是一种多分量自适应信号分解的新方法[11]，与传统信号分解方法相比，能够有效避免模态混叠和过分解等缺陷[12]。VMD利用变分约束将给定信号f分解为K个模态函数mk(t)，各个本征模函数IMF的带宽特定有限，且每个模态函数都分布在中心脉动频率周围，变分约束模型表达式为[13]

(7)

式中:{mk}为分解得到的K个IMF分量，{mk}={m1,m2,…,mk}；σ(t)为脉冲函数；{wk}为各IMF分量的中心频率，{wk}={w1,…,wk}。

为了完成输入信号f的自适应分解，得到带宽之和最小的IMFs，引入拓展的Lagrange表达式

L(mk,wk,λ)=

(8)

式中：α为惩罚因子，确保信号重构的准确性；λ(t)为拉格朗日乘子，用来强化约束的严谨性；〈·〉为内积运算；δ(t)为脉冲函数。

为解决以上变分约束问题，采用对偶分解和交替方向乘子算法[14]，一直更新mk,wk与λ(t)，使其循环迭代求取式(8)的鞍点，即为式(7)的最优解，模态分量函数mk和中心频率wk，如式(9)和式(10)所示

(9)

(10)

(11)

VMD在对振动响应序列进行分解时，模态总数K的确定是至关重要的一步，模态参数K的选取极大影响结果的准确性[15]。若K值大于信号分解得到有用成分的个数，则会产生信息叠加；若K值小于信号分解得到有用成分的个数，导致部分有限带宽的固态模量不能被分解出来。针对K值选取问题提出基于互信息法的改进变分模态分解方法。

互信息(mutual information，MI)反映两个随机变量间的关联性，能更好地辨别相关程度[16]。互信息表示为

I(X,Y)=H(Y)-H(X|Y)

(12)

式中：H(Y)为Y的熵;H(Y|X)为X已知时Y的条件熵。当I(X,Y)=0时，X与Y相互独立。

计算IVMD分解得到的各IMF分量与原始信号的互信息Ik，并利用式(13)进行归一化处理，进而判断各模态分量与原始信号的相关性，即原信号是否完全被分解。

(13)

式中,σi为求得各IMF分量的归一化互信息值，i=1,2,…,k。当σi低于σ=0.02时，认为IMF分量中已经不含有效的特征信息，原信号已分解完毕，停止运算。

采用互信息法自适应确定K值的具体算法流程如下：

步骤1初始化n=n+1,令K=1；

步骤2K=K+1,执行外层循环；

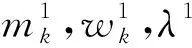
步骤4令n=n+1,执行内层循环；

步骤5对一切w≥0，根据式(9)和式(10)分别更新mk和wk；

步骤6由式(11)更新λ；

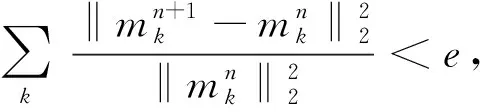
步骤8循环步骤2～7直至设定阀值σ大于原信号f分解得到的各IMF与f的归一化互信息值σi，即I(f-∑mk,f)<σ，结束循环。

2 管道振动响应混沌特性分析

以某泵站2号压力管道为研究对象，在主管和两个支管上共选取6个测点，每个测点的x,y,z三个方向各布置1个891-2型拾振器(档2)，测点布置如图1所示。

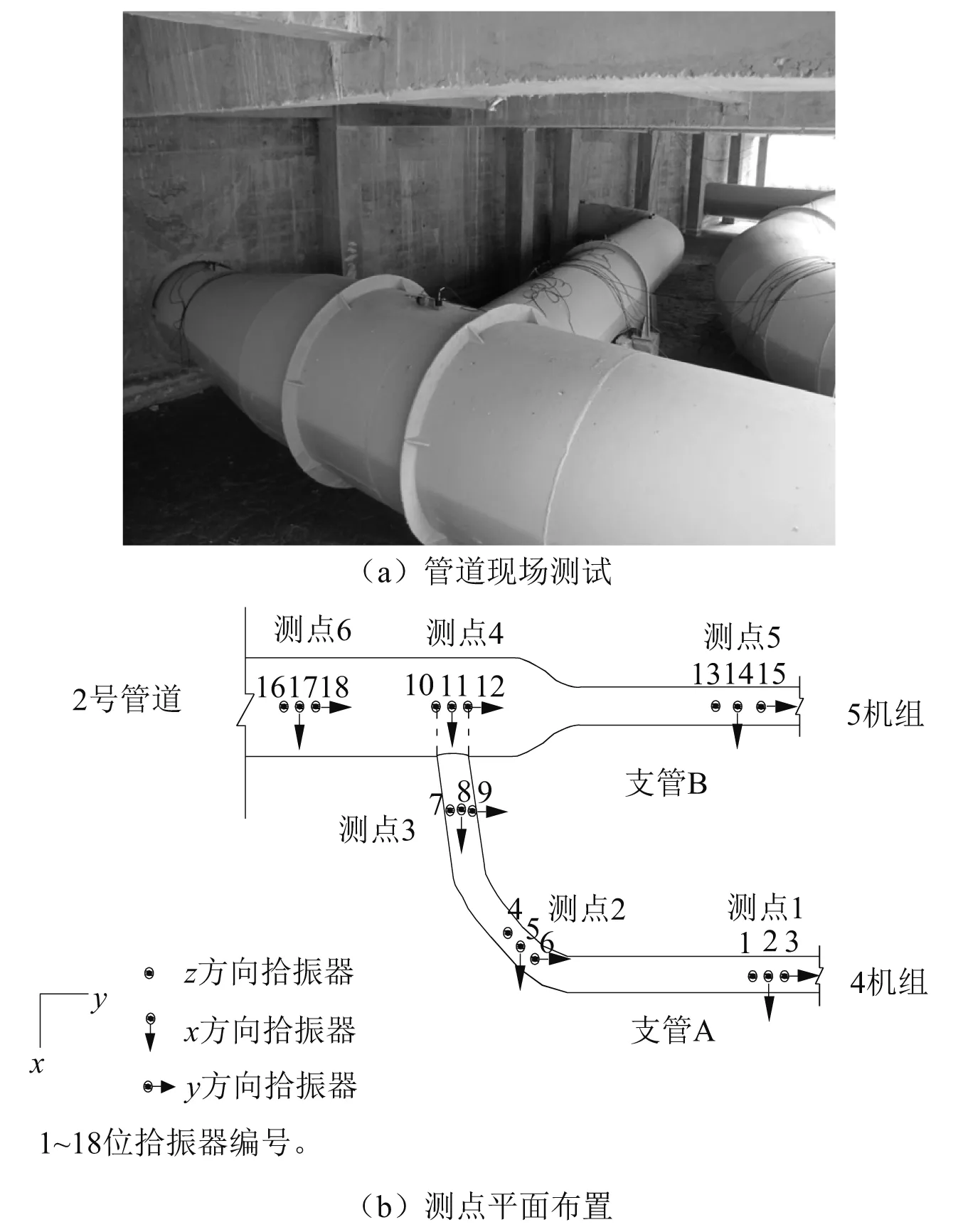
图1 管道测点布置图Fig.1 Layout of pipeline measuring points

原型试验共选取了4种工况采集管道振动响应，各工况描述、采样时间及采样频率，如表1所示，典型振动响应时程如图2所示。

表1 管道原型试验测试工况Tab.1 Test conditions of pipeline prototype

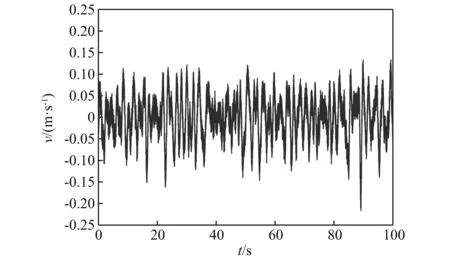
图2 工况4测点1 z向振动Fig.2 Point 1 of condition 4 of z-axis

首先，对管道振动响应时间序列进行相空间重构，即计算时间延迟τ和嵌入维数m。通过多向比较选取自相关函数法求取τ，选取CAO法求取m，限于篇幅，只列出工况4测点1z向振动响应的τ和m计算过程。

在自相关函数法计算τ的过程中，当函数值下降到初始值的(1-1/e)时，对应的τ值即为所求时间延迟。自相关函数计算结果如图3所示。

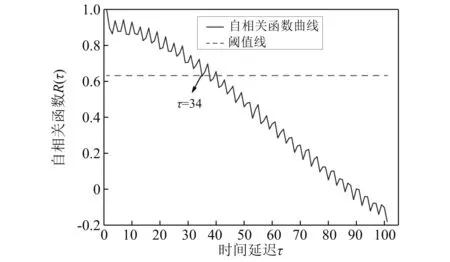
图3 工况4测点1 z向振动τ计算图Fig.3 τ calculation of point 1 z-axis vibration under condition 4

τ值确定后，采用CAO法确定嵌入维数m。E1(m)用来确定最小的嵌入维数m，即当E1(m)随m趋于平稳时对应的m值即为最小嵌入维数。参数E2(m)用于表明时间序列特性，即对任意m，若E2(m)都在 1 附近，则表明该时间序列是随机序列。具有混沌特性时间序列的E2(m)值逐渐接近 1，可通过此特征定性直观的判断一个时间序列是否具有混沌特性。当E1(m)不再随嵌入维数明显变化，且E2(m)函数值趋于1时，对应的m值即为最优嵌入维数。由图4可知，工况4测点1z向振动响应的最优嵌入维数m=11。

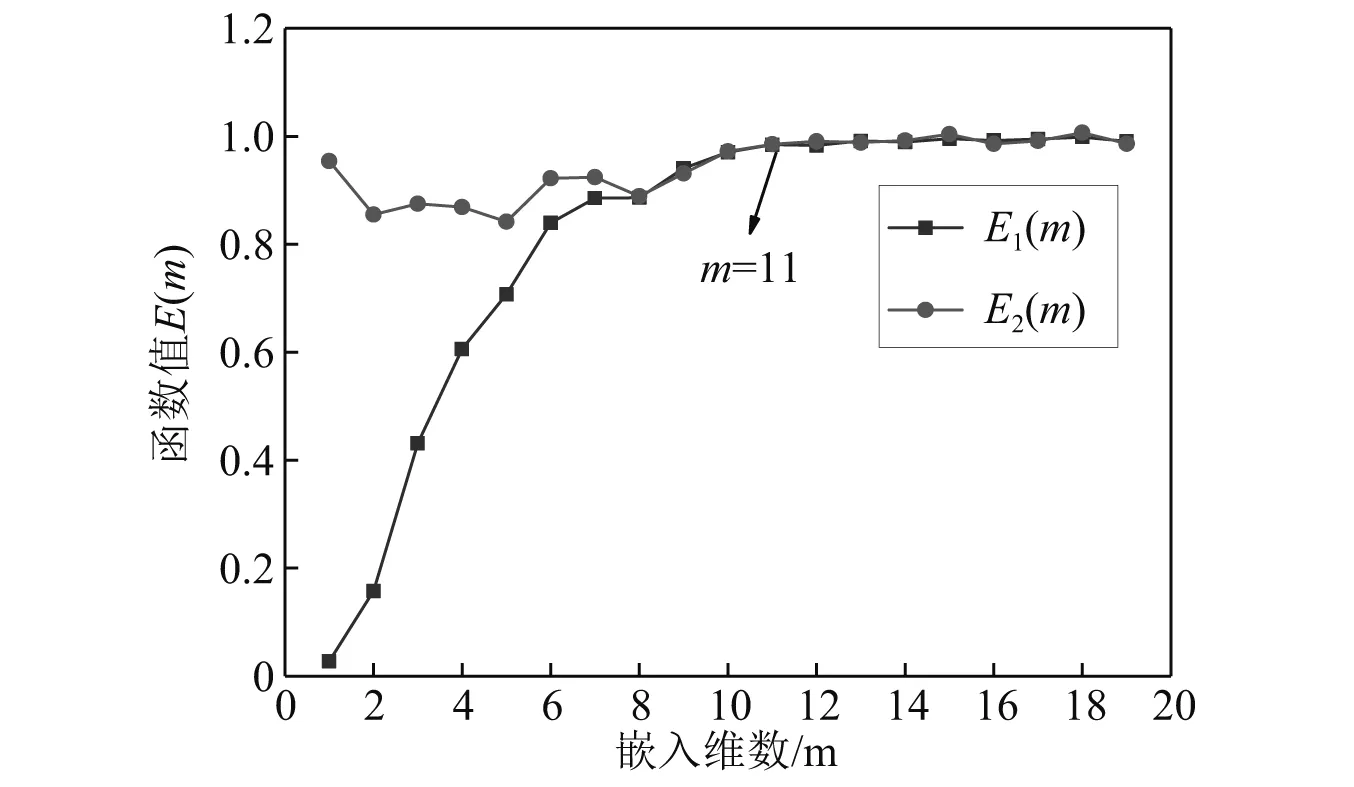
图4 工况4测点1 z向振动m计算图Fig.4 m calculation of point 1 z-axis vibration under condition 4

其次，选取饱和关联维数法、G-P算法[17](Grassberger和Procaccia提出的一个从单变量时间序列计算吸引子饱和关联维数的算法，简称G-P算法)及小数据量法分别计算饱和关联维数和最大Lyapunov指数，并利用两种指标进行混沌特性分析。

依据前文计算所得最佳时间延迟τ，嵌入维数取m=2,4,6,…,20，按式(3)中关联函数关系分别作不同m的log2C(r)～log2r对数关系曲线图，并选取其中的近直线段拟合其斜率，该斜率即为对应嵌入维数下的关联维数，随着嵌入维数的增加，关联维数达到饱和值时即为饱和关联维数D2。典型测点的饱和关联维数计算图，如图5所示。顺箭头方向分别为m=2,4,6,…,20时的关系曲线。

图5 工况4测点1 z向振动D2计算图Fig.5 D2 calculation of point 1 z-axis vibration under condition 4

为揭示关联维数计算值分布规律，作不同工况下各方向测点振动响应饱和关联维数D2变化曲线，如图6所示。

由图6可知：①整体而言，关联维数分布在1.156～5.283，说明管道各向振动响应具有混沌特性；②对比三个方向振动响应，主管道轴向(y向)测点关联维数明显小于其他两方向测点，表明管道轴向振动呈现出较低维的混沌吸引子，需要较少的独立控制变量即可描述其动力系统的变化规律；③同测点下，工况4(4机组、5机组稳定运行)各测点饱和关联维数D2值大于其他工况，而工况3(4机组单独关闭)相应D2值小于其他工况，说明机组的运行增加了管道振动的不确定性；④同工况下，靠近机组测点1、测点5及管道岔管处测点4的D2值相对较大，表明泵站管道振动复杂性受机组及流态影响较大。

图6 各方向测点关联维数变化曲线Fig.6 Curves of correlation dimension of points in different directions

为对比验证上述结果，利用最大Lyapunov指数λ1对泵站管道的混沌特性做进一步分析。根据前文求得时间延迟τ和嵌入维数m，采用小数据量法计算最大Lyapunov指数λ1。图7为典型测点λ1计算图，可知分离因子y(i)函数值在近线性增长后趋于稳定，通过最小二乘法拟合增长段直线斜率，该值即为λ1。不同振动方向测点λ1值，如图8所示。

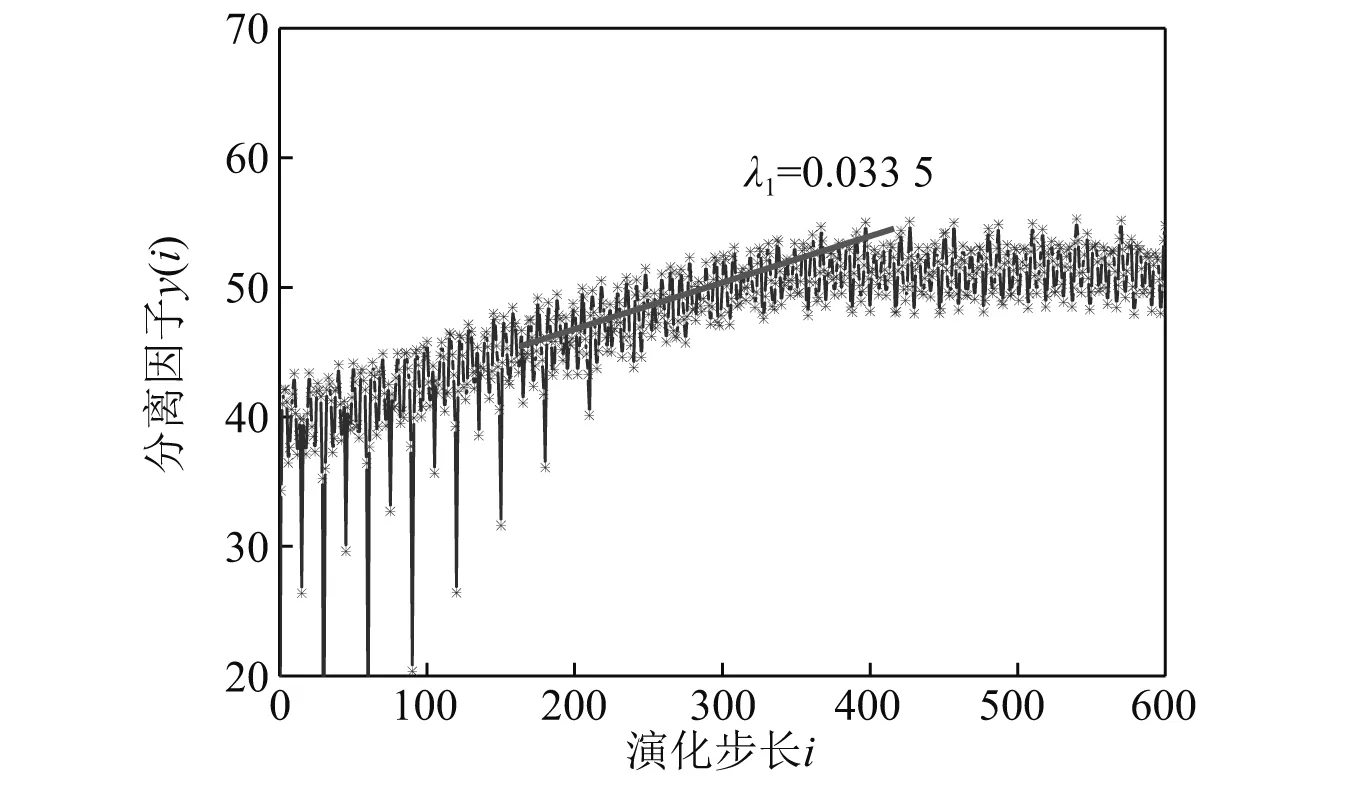
图7 工况4测点1z向λ1计算图Fig.7 λ1 calculation of point 1 z-axis vibration under condition 4

由图8可得： ①各测点不同工况下最大Lyapunov指数λ1取值在0.032 3～0.073 4，均大于零，说明管道实测振动响应具有明显的混沌特征；②工况4(4机组、5机组稳定运行)各测点λ1相较其他工况更小，而工况3(4机组单独关闭)λ1值相对偏大，可知随着工况中两机组的开启，最大Lyapunov指数λ1取值随之减小，表明随着机组稳定运行，流态逐渐稳定，管道振动的混沌特性逐渐减弱；③同工况下，靠近机组测点1、测点5λ1值较小，而管道岔管处测点4λ1值较其他测点更大，说明岔管处流态使管道振动更具有混沌特性。上述分析与关联维数D2计算结果互为补充，说明机组运行时流态对泵站管道混沌特性的影响较大。

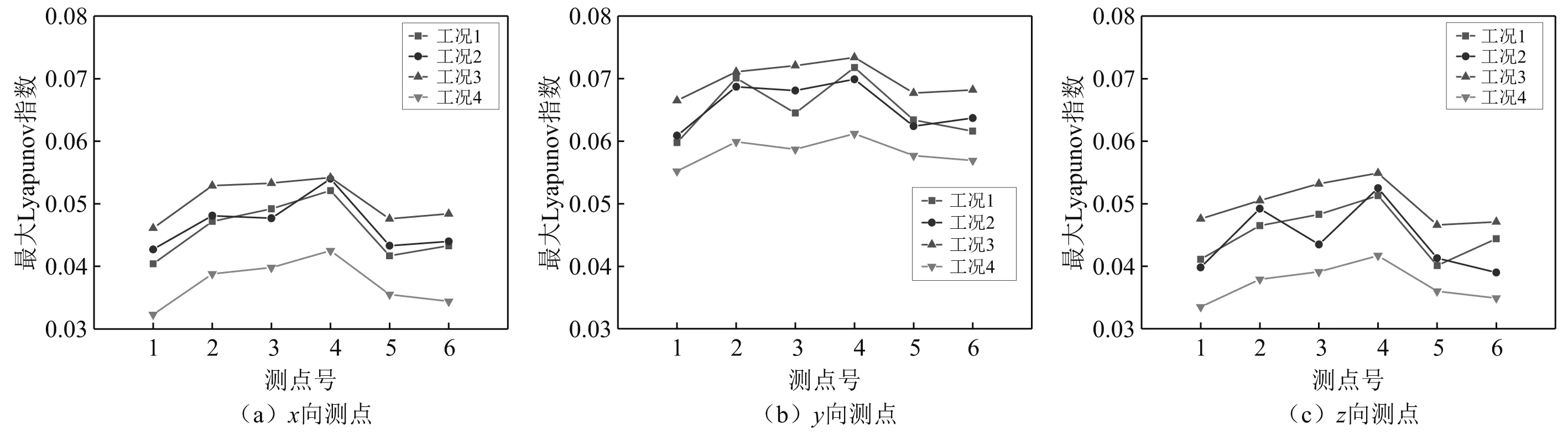
图8 各方向测点最大Lyapunov指数变化曲线Fig.8 Curves of largest Lyapunov exponent of points in different directions

3 基于IVMD的多尺度混沌特性分析

泵站管道的振动特点具有不同于一般输流管道的特殊性，这主要体现在泵站机组对连接管道振动的影响方面，其振源组成主要为管道输水流动产生的低频水流脉动以及机组运行产生的叶频、转频及倍频等。以工况4测点1z向振动响应为例，对其进行频谱分析如图9所示。参考文献[18]，20 Hz,40 Hz及60 Hz分别为机组旋转倍频及转轮叶片振动频率，而0.5 Hz为泵站管道输水湍流产生的水流脉动激励频率。可知水流脉动产生的管道振动激励频带(0.5 Hz)相对较宽，宽峰功率谱属于混沌系统的典型特征；机组运行产生的管道振动激励(20 Hz,40 Hz,60 Hz)对应尖峰功率谱，周期性强，故推测泵站管道的混沌特性主要是输水管道内湍流脉动引起的，而机组振动掩盖了泵站管道的混沌特性。

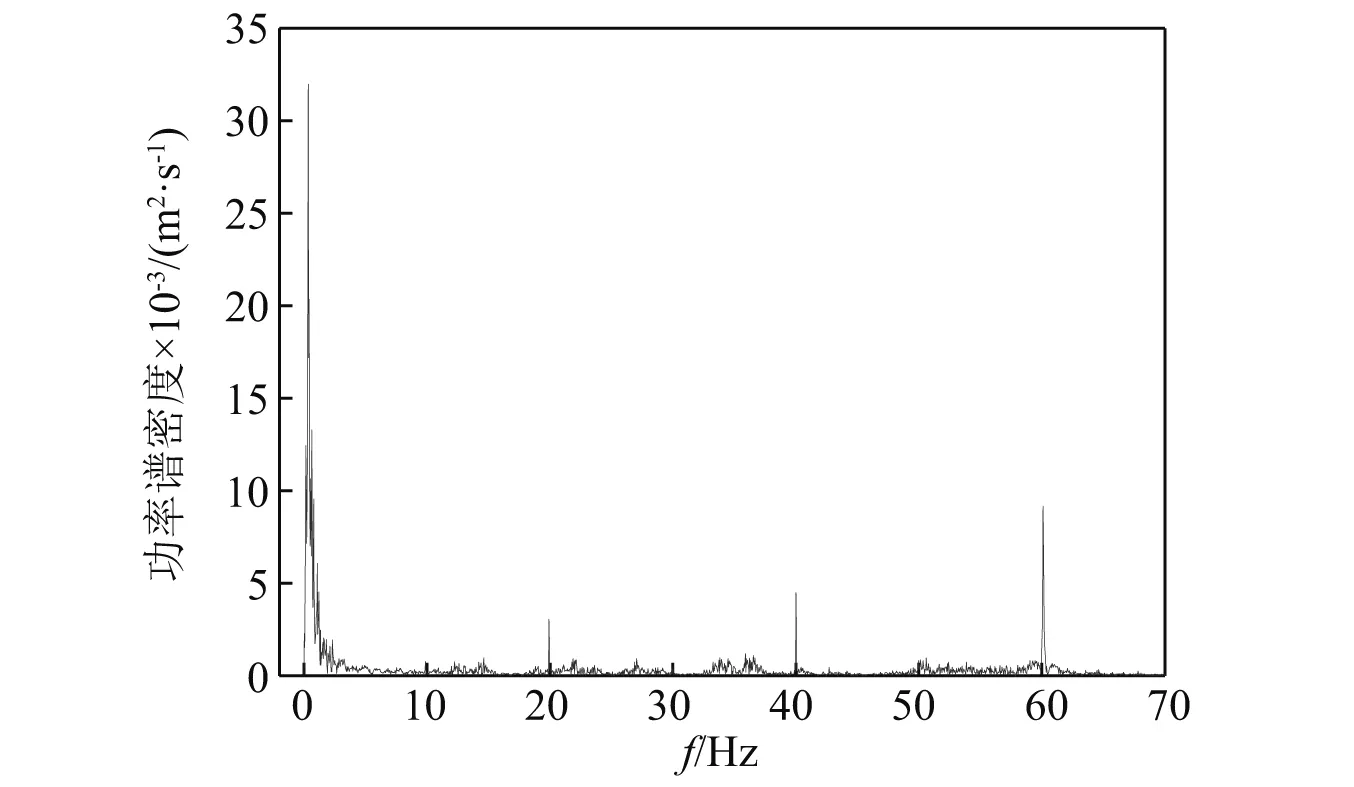
图9 工况4测点1 z向振动响应频谱图Fig.9 Spectrogram of point 1 z-axis vibration response under condition 4

为明晰使管道振动响应具有混沌特性的振动激励，采用IVMD方法识别引起管道混沌特性的振动激励源。

利用互信息法确定IVMD的模态参数K=4，管道工况4测点1z向振动响应经IVMD分解获得4个IMF分量。分解所得IMF分量时程如图10所示，各IMF分量与原振动序列的归一化互信息值，如表2所示。

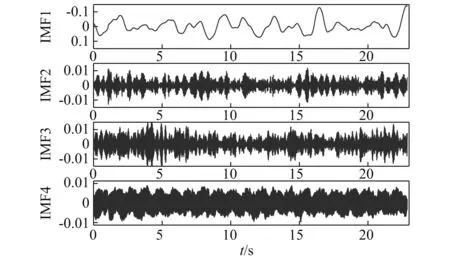
图10 振动响应IVMD分解IMF时程图Fig.10 Time histories of IMFs decomposed by IVMD

表2 振动响应各IMF归一化互信息值Tab.2 IMF normalized mutual information value of vibration response

由表2可知，4个IMF分量归一化互信息值均大于阀值0.02，满足分解要求。由图10可知，原振动响应经IVMD分解后可得4个频率依次增加的IMF分量，经频谱分析可得IMF1～IMF4的频率分别对应原响应频谱图中4个主要频率带：0.5 Hz，20 Hz，40 Hz，60 Hz。利用饱和关联维数和最大Lyapunov指数对分解所得各IMF进行混沌特性分析。

典型IMF混沌特征值计算过程如图11所示，由图11(a)、图11(b)可以看出，IMF1饱和关联维数D2=1.115，最大Lyapunov指数λ1=0.077 4，具有明显混沌特性；IMF2～IMF4均无法找到D2对数曲线中近线性区域，无混沌特性，限于篇幅仅给出IMF2对数曲线斜率如图11(c)所示，顺箭头方向分别为m=2,4,6,…，20时的关系曲线。

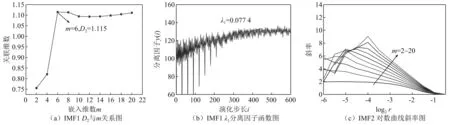
图11 典型IMF分量混沌特征值计算图Fig.11 Calculation of chaotic eigenvalues of typical IMFs

对比分析可得：①代表湍流脉动激励的IMF1饱和关联维数1.115为分数维，且最大Lyapunov指数0.077 4大于零，具有明显混沌特性；代表机组运行振动激励的IMF2～IMF4无混沌特征，表明机组的运行并不能引起泵站管道振动的混沌特性；②剔除无混沌特性的机组运行振动激励成分(IMF2～IMF4)后，管道振动响应关联维数D2由4.985降低至1.115，而最大Lyapunov指数λ1由0.033 5增大至0.077 4，即管道振动的复杂性下降，其混沌特性更为明显，表明泵站管道振动时，输水湍流激励使其振动具有混沌特性，而机组运行产生的振动激励掩盖了泵站管道的混沌特性，增加了管道振动的不确定性。

4 结 论

(1)不同工况下泵站管道测点振动响应饱和关联维数D2均存在，说明泵站管道振动具有混沌特征。

(2)不同工况下各测点最大Lyapunov指数λ1在0.051 3～0.077 4，随着工况中两机组的开启，最大Lyapunov指数λ1取值随之减小，表明随着机组稳定运行，流态逐渐稳定，管道振动的混沌特性逐渐减弱。

(3)湍流脉动是引起泵站管道产生混沌特性的主要原因，而机组振动掩盖了泵站管道的混沌特性，增加了管道振动的不确定性。