垂向载荷作用下的冰层破裂及其影响因素分析
汪春辉, 朱广元, 王 超, 郭春雨, 王嘉安
(哈尔滨工程大学 船舶与海洋工程学院,哈尔滨 150001)
在极区,冰层常被用作道路、机场、停车场和建筑平台,此时冰层会受到自上而下的垂向载荷;当冰层下航行潜艇上浮并穿透冰层露出水面时,冰层受到自下而上的垂向载荷。因此,垂向载荷作用下的冰层破裂过程及其影响因素的分析研究,对于极区军事、科研和勘探活动的安全进行具有十分重要的意义[1]。
冰层在垂向载荷作用下的断裂破碎是一个非常复杂的过程,不仅与冰的物理力学性质有很大关系,还与冰与结构物接触角度、接触面积和相对速度等有关。到目前为止,冰层在垂向载荷作用下的破裂研究主要集中在试验和数值研究两个方面。Frankenstein[2-3]进行了淡水冰层的全尺寸突破载荷试验,描述了集中载荷和均布载荷下冰层的破裂现象。Gold[4]绘制了浮冰厚度与突破载荷关系曲线图,并发现载荷大多数在350h2~7 000h2,其中h为冰层厚度。Sodhi[5]进行了一系列小规模试验,用不同直径和端部形状的圆柱形压头,以恒定速度将漂浮的冰层垂直向上推,并测量由此产生的相互作用力。Beltaos[6]结合冰的黏弹性性质和冰层的破坏模式,分别将冰的应力、应变、挠度和应变能作为失效判据,并进行对比。Kujala等[7]为探究冰的弯曲破坏行为进行了一系列全尺寸试验和模型试验。试验研究手段能够有效地观测冰在垂向载荷作用下的破坏模式,然而在试验过程中,冰样品的制作没有统一的规范标准,且试验过程不能有效定量地控制影响变量,因此,仍需要理论和数值方法辅助研究冰的力学特性。随着数值模拟技术的进步,有限元方法作为一种可以考虑冰作用机理的数值手段正在成为解决冰与结构物相互作用问题的一种有效方法:Gagnon[8]在LS-DYNA软件中采用了一种“可压碎泡沫”线弹性硬化材料作为冰本构模型,通过数值模拟预报了循环锯齿载荷和压力分布,该数值模型与试验观测冰力学特征基本相同。Daiyan等[9]模拟了北极海域海上结构物与浮冰、冰脊等之间的相互作用,数值模拟与解析方法对比分析误差在15%左右。Gao等[10]提出了一种用各向同性材料来模拟极限条件下的船-冰山碰撞,并通过LS-DYNA中的用户自定义模块编译了冰的本构模型,结果表明,该各向同性材料能够很好地体现冰山力学行为。郭春雨等[11]基于LS-DYNA软件进行了冰区船舶在碎冰区域的航行阻力预报,成功模拟了碎冰与船舶相互作用的典型物理现象。武文华等[12]进行了海冰与锥体抗冰结构动力作用的数值模拟,其模拟结果与实测海冰的弯曲断裂过程结果相符。最近,无网格方法也在冰冲击问题领域展露头角[13-14],然而这些方法仍处于起步阶段,还需投入大量的研究工作。
从上述文献中可以发现:基于LS-DYNA商用软件的冰力学行为研究是现下常用的且较成熟的一种预报冰与结构物作用的数值研究方法。LS-DYNA中基于von Mises屈服准则的弹塑型本构模型已广泛应用于冰本构模型建立中:文献[15-19]将分段线性弹塑性材料应用于船冰等冰与结构物研究,可较好地模拟冰材料失效变成碎冰的过程;Das等[20-21]采用一种典型的各向同性的弹塑性材料模拟冰的弯曲行为,破裂过程以及弯曲强度与试验结果相符。然而,仍缺少关于冰层在垂直载荷作用下破坏特性方面的研究。因此,本文在上述学者建立的冰本构模型基础上,深入研究了平整冰层在垂向载荷作用下的破坏过程,分析了冰与结构物不同接触角度、接触面积以及相对速度等因素对冰层突破载荷的影响,为在冰层上从事科研和建设活动提供一种作为安全判据的数值模拟方法。
1 理论基础
1.1 冰本构模型
在本文的数值模拟研究中,所选冰本构材料是LS-DYNA中的124号材料*MAT_PLASTICITY_COMPRESSION_TENSION[22],124号材料是一种弹塑性应变率模型,旨在模拟冰行为,该材料的von Mises屈服准则为
(1)
式中:J2为第二应力不变量;σy为屈服应力。
第二应力不变量J2根据偏应力分量Sij定义为
(2)
屈服应力σy的表达式为
σy=σ0+Epεeff,p
(3)
式中:σ0为初始屈服应力;εeff,p为有效塑形应变;Ep为塑形硬化模量。
另外,对于压缩和拉伸,可以定义一个独特的屈服应力与有效塑性应变曲线。名义应力的符号决定张力,其中正应力表示拉伸状态。黏性应力张量叠加在塑性产生的应力张量上,两条载荷曲线ft(p)和fc(p),分别为在拉伸和压缩状态下的屈服应力σy和有效塑形应变εeff,p的关系。当超过名义拉伸应力和名义压缩应力pt和pc时,分别确定是否遵守拉伸或压缩曲线。如果应力p在两个值之间时,两条曲线之间的一个加权平均值pf将被使用。
(4)
最终应力由如式(5)计算
σ=dedp(σ′-p)
(5)
式中,de和dp分别为与塑性应变和应力引起的失效相关的损伤变量。塑性应变的破坏准则为
(6)
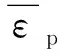
对于压力,由式(7)决定
(7)
式中:pf,t为失效应力;pc为应力截止值。
1.2 罚函数接触算法
在LS-DYNA中,罚函数接触算法首先需要将可能发生接触作用的两个表面分别定义为主表面和从表面,在每一个时间步计算之前先检查各从动点是否穿透主动面,若不穿透则不进行处理,若发生穿透就在主表面和从表面之间放置一系列法向弹簧,弹簧的作用是为了限制穿透,其大小与穿透深度以及接触刚度成正比。罚函数算法对所有节点同时进行上述处理,算法逻辑简单,很少引起沙漏效应。同时,由于算法本身的对称性导致无噪声。
罚函数法的接触力由式(8)得出[23-24]
F=kδ
(8)
式中:k为单元接触面刚度;δ为穿透量。
(9)
式中:pf为单元接触面刚度的惩罚因子;K为接触单元体积弹性模量;A为接触段面积;V为主段体积。
2 计算方法验证
Sodhi[25]通过三种方法来确定穿透冰层所需的载荷,指出冰层在垂向载荷作用下的破坏方式主要以弯曲破坏为主,冰的弯曲强度对冰层的破坏效果有很大影响。因此,本文通过对冰的四点弯曲模型试验进行模拟,来验证文中模型模拟冰弯曲破坏过程的可靠性。本文选取Kujala等为探究冰弯曲破坏行为进行的一系列全尺寸试验和模型试验为验证案例。本次模拟中,选取梁尺寸4.320 m×0.365 m×0.392 m,上下支座间距(D)为1.5 m,四点弯曲试验数值模拟的几何模型,如图1所示,上方的支撑刚性固定,下方的支撑匀速向上移动。冰的力学参数和计算参数设置主要参考文献[25-27],如表1所示。
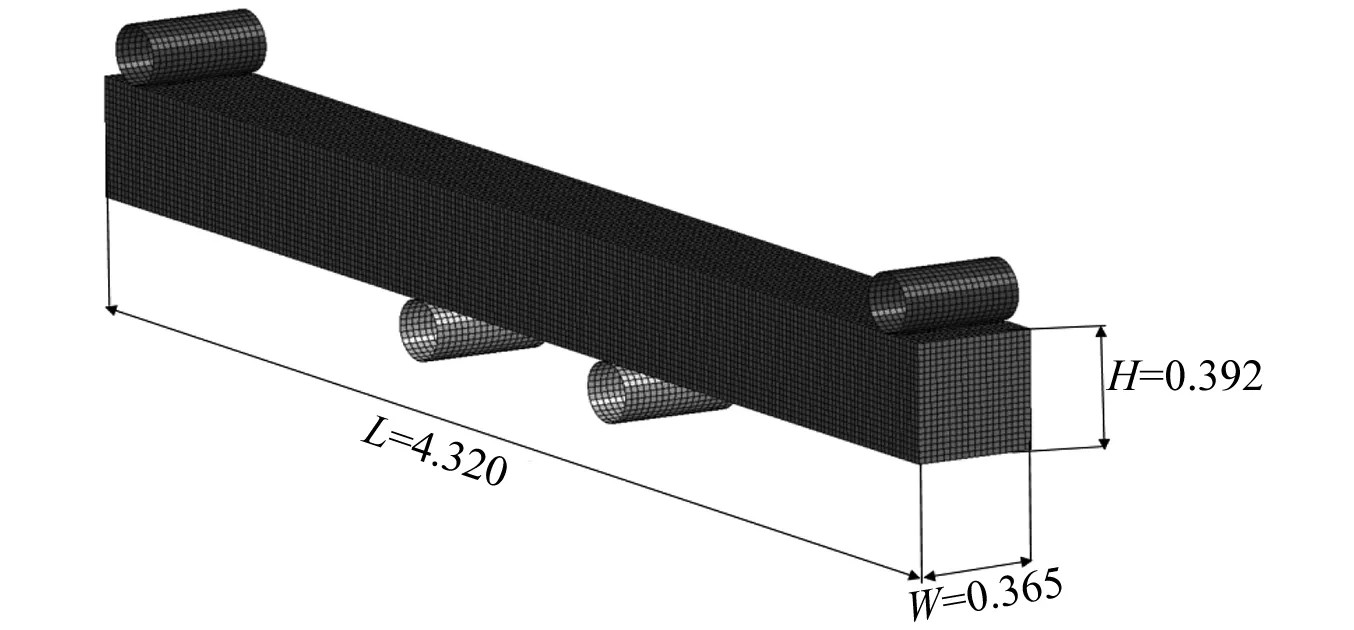
图1 四点弯曲试验的几何模型(m)Fig.1 Geometric model of four point bending test(m)

表1 试验工况设定和海冰参数Tab.1 Test conditions setting and sea ice parameters
在四点弯曲试验中,两个压载点之间的梁承受恒定的弯矩,且不受压载点向下压缩的影响。通过四点弯曲试验,可以确定最大弯曲载荷和弯曲裂纹位置,弯曲时的理论破坏载荷可由式(10)计算
(10)
式中,W,H和D分别为梁宽、高度和上下支座之间的距离。该试验中,最大弯曲力矩发生在梁中部位置。由此,计算过程中监测梁中部位置的应力变化曲线,再通过式(10)换算得到弯曲破坏载荷。数值计算结果如图2所示。

图2 四点弯曲试验数值模拟结果Fig.2 Numerical simulation results of four point bending test
从图2(a)可以观测到,冰受到弯曲载荷后在加载支撑处形成裂纹并断裂,此现象和试验结果有较高的一致性,且与光滑粒子流体动力学(smoothed particle hydrodynamics,SPH)法计算结果(见图2(b))进行对比,冰的断裂现象吻合度极高。四点弯曲破坏的弯曲载荷-时间曲线绘制在图2(b)中,可以发现试验结果和数值计算结果的趋势以及峰值点基本一致。本文模拟得到的断裂发生时间和载荷结果,以及Kujala等和Das等采用SPH法得到的数值模拟结果和模型试验结果,如表2所示。从表2的数据以及冰的破坏现象可以说明本文中的本构模型具备模拟冰弯曲破坏过程的能力。

表2 断裂发生时间及载荷结果对比Tab.2 Comparison of fracture occurrence time and load results
3 冰层在垂向载荷作用下的破坏
3.1 计算模型与参数设定
本文旨在研究冰层在圆柱体垂直作用下冰层破裂过程及其影响因素。根据Sodhi研究中冰层的穿透或突破过程中的大挠度局限于接近施加载荷的区域,通常小于冰厚度的10倍~20倍,本文所选冰层尺寸为0.60 m×0.60 m×0.02 m,冰层尺寸为冰厚的30倍,所选的冰层尺寸大小满足相关文献,既不会对圆柱体与冰层的穿透过程及突破载荷产生影响,又可以使计算模型适中降低计算时间。本文数值模拟选择的冰层以及圆柱尺寸,如图3所示,圆柱放置于冰层正中心下0.01 m处。

图3 圆柱体撞击冰层数值模型(m)Fig.3 Numerical model of rigid cylinder impacting on ice (m)
在数值模拟计算中,不考虑圆柱的结构响应,将圆柱体设置为刚体,采用SHELL单元,同时给定圆柱体Z方向恒定的速度运动,约束其他5个自由度的运动。在计算过程中,圆柱体上升会不断地与冰面发生碰撞侵蚀,设置冰材料的失效准则,达到失效标准的单元会被删除,形成新的圆柱体-冰层接触面,继续完成下一阶段的圆柱体-冰层碰撞,其主要参数如表3所示。
1.2.2 动物分组 所有动物饲养于室温中,自由饮水饮食1周,然后按随机数字法将其分为正常对照组、慢性支气管炎模型组、杆努尽烟低剂量组、杆努尽烟高剂量组及桂龙咳喘宁阳性药物组,每组10只。

表3 主要材料参数Tab.3 Main material parameters
本文采用圆柱体-冰层相互作用接触算法(*CONTACT_ERODING_SINGLE_SURFACE和*CONTACT_ERODING_SURFACE_TO_SURFACE)模拟圆柱体-冰层的接触碰撞,使圆柱体在持续上升过程中不断与冰材料发生碰撞接触,冰单元不断发生破坏并通过删除失效单元,形成裂纹。将冰层边界条件设置为无反射边界,当数值模型中采用无反射边界条件时,LS-DYNA 会基于线性材料特性假设计算出所有无反射边界上的阻抗匹配函数,从而在边界上吸收并消除应力波,达到以有限域来表示无限域或者半无限域的目的,极大地减小计算模型的计算量。
3.2 单元收敛性分析
为验证冰网格选择合理,分别选取网格大小为0.001 8 m,0.002 5 m以及0.003 5 m的正方形网格进行收敛性分析。
如图4所示,选取圆柱上升距离为0~0.002 5 m,突破载荷在此阶段内冰层主要以弹性变形为主并伴随着轻微裂纹产生。图4中,三条曲线尽管在某些时间点仍存在振荡,但总体来看趋势相同,载荷特征稳定,当单元大小为0.002 5 m时,计算结果可认为达到收敛。
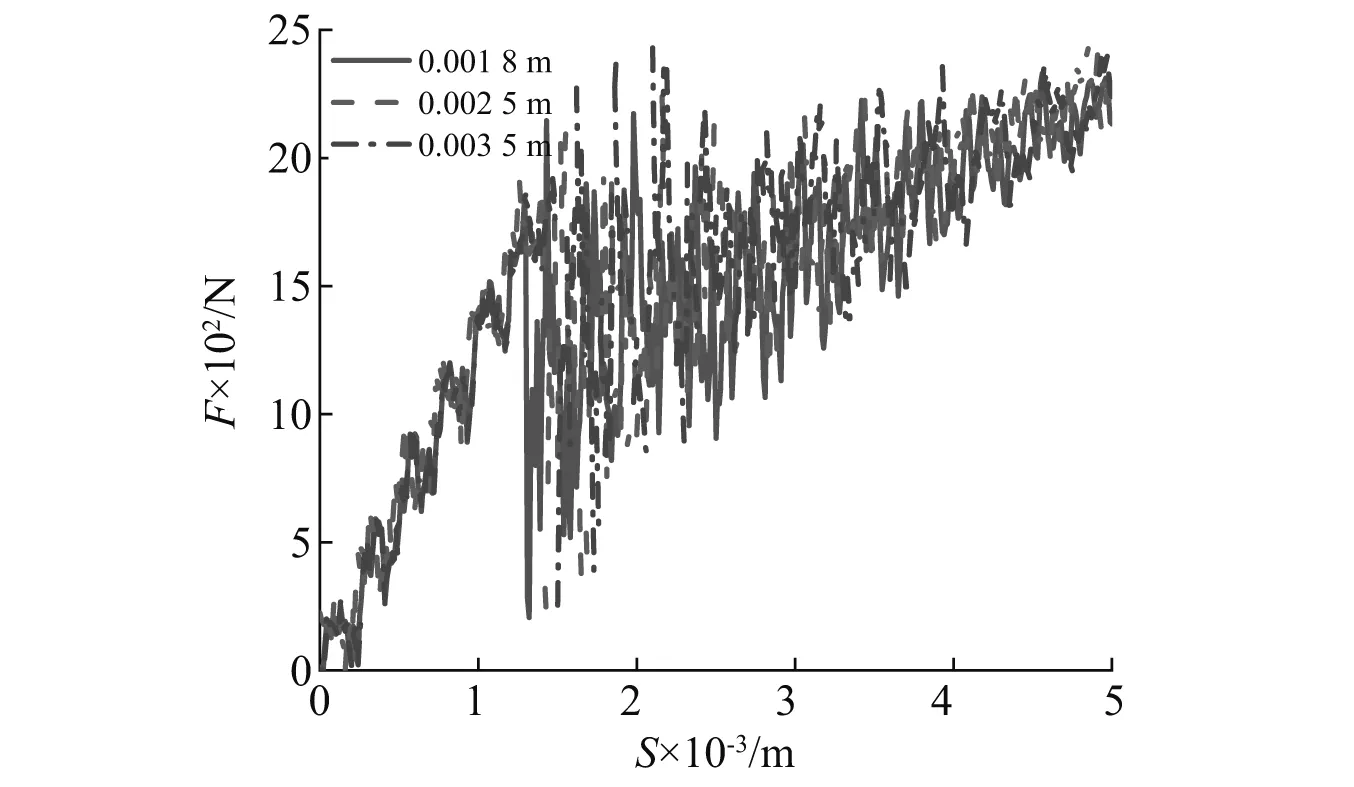
图4 不同网格尺寸下的突破载荷Fig.4 Breakthrough load under different grid sizes
3.3 垂向载荷作用下冰层破裂过程
选取圆柱体上升速度为0.1 m/s,冰层厚度为0.02 m的数值模拟结果进行分析,圆柱体上升距离为圆柱体与冰层接触开始之后圆柱体继续上升的距离。数值模拟获得的裂纹扩展过程,如图5所示。图5中:左侧为Beltaos的研究结果;右侧为本文计算结果;当圆柱体接触到冰面时,冰面接触点处立即发生弯曲破坏,产生径向裂纹,见图5(a);随着圆柱不断上升穿越冰层,径向裂纹数量增加呈圆周式分布在接触点向外四周,见图5(b)和图5(c);当径向裂纹扩展足够充分,外层生成圆周向的裂纹,见图5(d)。对比数值结果的裂纹扩展和试验给出的裂纹生成图可以发现,数值结果能够模拟裂纹的生成和扩展,并且与试验现象一致。
冰层的突破载荷随圆柱上升距离的变化大体上可以分为三个阶段,如图6所示。在A阶段,冰层与圆柱体初始接触,冰层发生弹性变形,突破载荷与上浮距离成线性关系,突破载荷迅速增加。当上升距离达到0.001 46 m时,由于冰层弹性变形产生的最大拉应力超过冰的抗拉强度,浮冰板上层形成径向裂纹,对应于图5(a),此时发生轻微卸载。径向裂纹的形成是冰层上高负荷的表现,但引起径向裂纹的载荷远小于圆柱体最终穿透时的载荷。在B阶段,随着圆柱体继续上升,冰层在形成径向裂纹之后,突破载荷继续上升,但上升距离-突破载荷的斜率下降,在此过程中裂纹在载荷作用下向外扩展相当长的一段距离。直到圆柱上升距离到达C阶段,冰层上径向裂纹大量生成,对应于图5(b),突破载荷再次出现卸载现象,上浮距离-突破载荷斜率逐渐降低。尽管形成了大量裂纹,但冰层不会突然失效,仍然能承受圆柱体的作用,这可能是由于断裂的冰被一个完整的冰层所包围,它抑制了冰块的膨胀,并在冰块之间引起楔入作用,对应于图5(c)。圆柱继续上升,当圆柱上浮至0.012 m时,突破载荷达到最高值,由于在冰层的上表面和下表面存在大量裂纹施加的拉应力造成冰层破裂,突破载荷骤然下降,到达极低值,此时圆柱突破冰层。
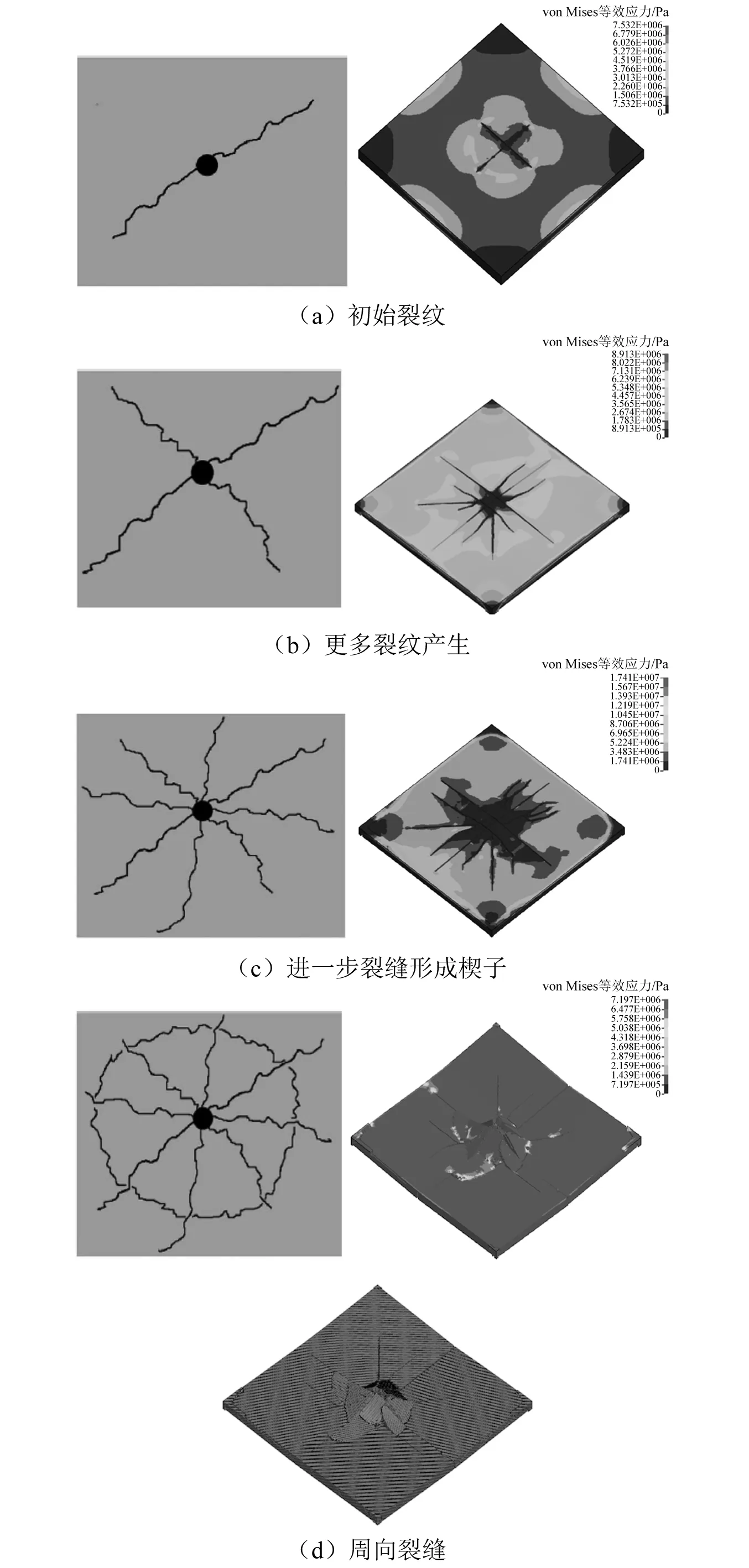
图5 裂纹扩展过程Fig.5 Crack growth process

图6 为突破载荷F随圆柱上升距离S变化曲线Fig.6 Variation curve of breakthrough load F with cylinder rising distance S
3.4 不同接触面积对冰层破裂的影响
为研究圆柱体与冰层在不同接触面积下对冰层破裂的影响,根据施加载荷的径向范围可将载荷分为集中载荷和均布载荷,由Frankenstein的研究可知,载荷径向范围(D)大于两个冰厚(H)的载荷可认为是均布载荷,反之,即为集中载荷。在本文中通过选取直径分别为0.06 m和0.03 m的圆柱,即D/H=3.0和D/H=1.5来实现均布载荷和集中载荷作用下的冰层破坏模拟,圆柱模型如图7所示。不同直径圆柱作用下冰层突破载荷计算结果,如图8所示。
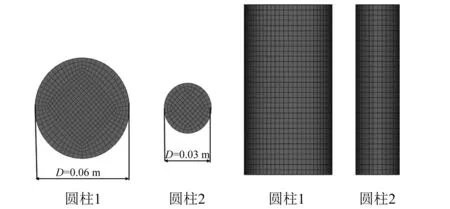
图7 圆柱模型Fig.7 Cylindrical model

图8 不同直径圆柱作用下冰层突破载荷Fig.8 Icebreak load under different diameter cylinders
由图8可知,圆柱1和圆柱2作用下的冰层突破载荷的分布趋势基本相同,但是圆柱2的载荷振幅要大于圆柱1的载荷振幅,这说明圆柱2与冰层之间的相互作用更加激烈。同时,圆柱2在上升0.007 48 m且突破载荷达到2 640 N后,冰层断裂,圆柱突破冰层,而圆柱1在上升0.009 85 m且冰载荷达到2 870 N后,冰层断裂,圆柱突破冰层。这说明在相同速度和冰厚的集中载荷作用下,冰层会在较小变形的情况下到达最大抗拉应力,相比于均布载荷,集中载荷更容易突破冰层。
为了进一步分析冰层在均布载荷和集中载荷作用下的破坏特征,现定义冰层突破过程的运动学几何参数,如图9所示[28]。图9中:PF为冰层最大承载载荷;r0为施加载荷半径;r1为周向裂纹半径;h为冰层厚度。不同直径圆柱作用下冰层的破裂现象,如图10所示。图10中:均布载荷(圆柱1)作用下的冰层r1/r0范围为1.5左右;集中载荷(圆柱2)作用下的冰层r1/r0范围为1.0左右。这说明均布载荷的冰层破坏更多为弯曲破坏,集中载荷作用下的冰层破坏更多为冲击破坏。

图9 压痕破坏运动学Fig.9 Indentation failure kinematics

图10 不同直径圆柱作用下冰层破裂Fig.10 Ice layer fracture under different diameter cylinders
3.5 圆柱不同上升速度对冰层破裂的影响
为研究圆柱体不同上升速度对冰层破裂的影响,针对所选冰本构材料是一种冰的高应变率失效模型,本文将圆柱体上升速度v分别设置为0.1 m/s,0.3 m/s,0.5 m/s,0.7 m/s,0.9 m/s,并开展相关计算。
圆柱体不同上升速度下冰层突破载荷和极值,分别如图11和图12所示。由图11和图12可知:圆柱体在上升速度为0.1 m/s,0.3 m/s,0.5 m/s时,突破载荷极值大小相差不大,而在 0.7 m/s和0.9 m/s时,突破载荷的极值有明显的增加;同时上升速度为0.5 m/s时的突破载荷极值为最小值。取圆柱体上升速度分别为0.3 m/s,0.5 m/s和0.7 m/s时,冰层的突破载荷,由图11和图12可知,较高的上升速度会使圆柱体与冰层之间的相互作用更加激烈,突破载荷在冰层破裂前圆柱体相同上升距离内有明显的增加,同时,这也导致了冰层破裂时的圆柱体上升距离随速度的增加而减少。在圆柱体上升速度为0.5 m/s时,突破载荷极值会出现拐点,这主要是因为在圆柱体上升速度为0.5 m/s时,冰层会在圆柱体较小的上升距离内发生断裂,冰层与圆柱体的接触程度不足;而在上升速度为0.3 m/s时,冰层上的裂纹生长速度较慢,冰层在圆柱体上升较大的距离之后发生断裂,突破载荷随着圆柱体的逐渐上升而增加,最终导致突破载荷极值高于上升速度为0.5 m/s时。随着圆柱体上升速度的增加,冰层突破载荷的变化过程也会发生较明显的变化,较高的上升速度使冰层无明显的弹性变形阶段。这是因为较高上升速度下圆柱体与冰层接触时产生的冲击载荷,使冰层瞬时产生了大量的裂纹,另外冰层突破载荷的装载和卸载现象明显,突破载荷峰值大小和出现次数明显增加,这是因为随着圆柱体上升速度的增加,冰层表面裂纹的数量增加与生长速度都要明显增快。
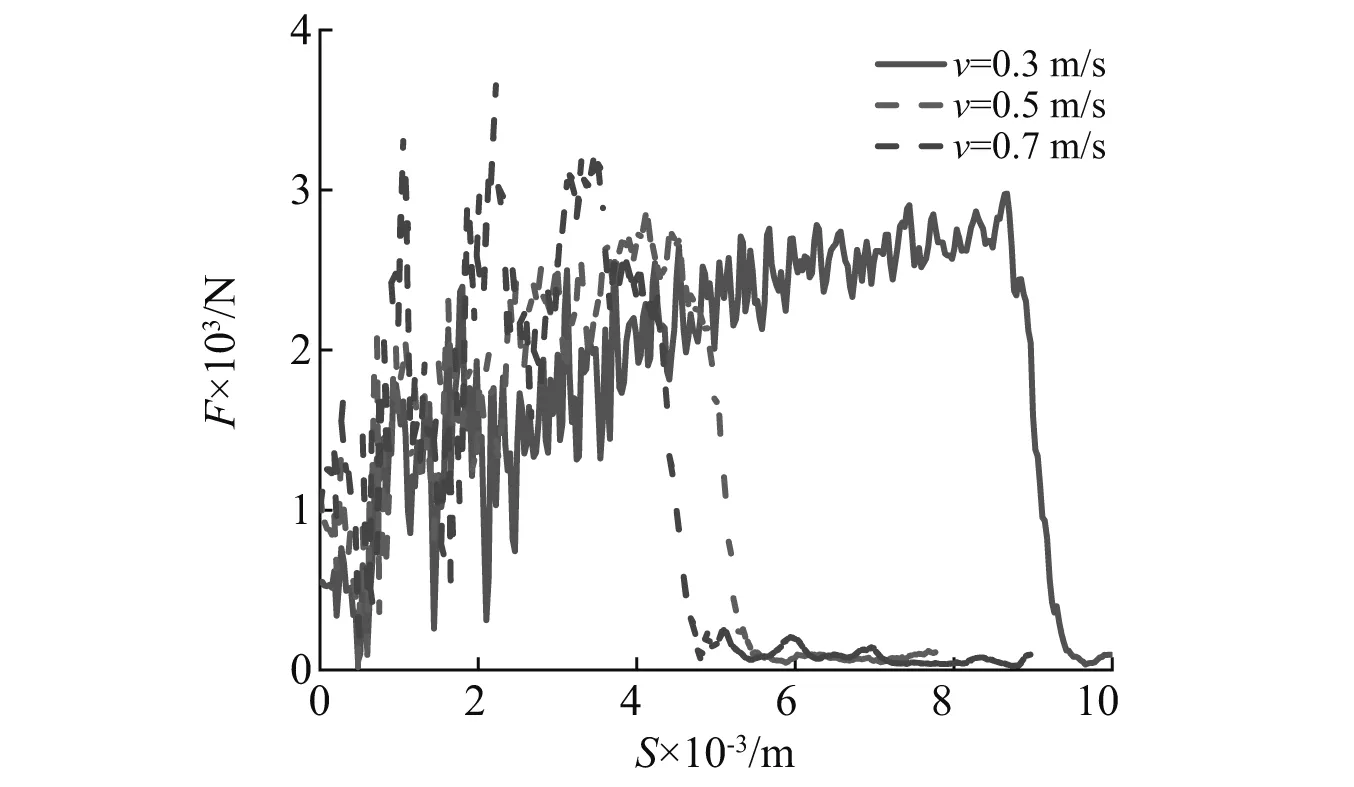
图11 不同上升速度下突破载荷曲线Fig.11 Breakthrough load curve at different rising speeds
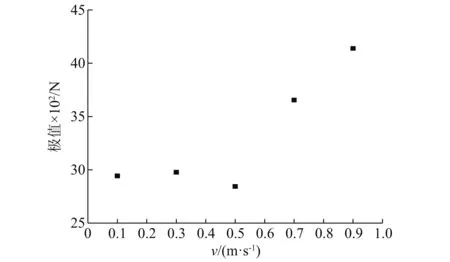
图12 不同上升速度下突破载荷极值Fig.12 Maximum breakthrough load at different rising speeds
3.6 不同接触角度对冰层破裂的影响
为研究不同接触倾角对冰层破裂的影响,本文通过将圆柱沿水平轴旋转一定的角度,使圆柱体表面与冰层表面形成一定的倾角,如图13所示。在本次数值模拟选取的接触倾角θ为1°,2°,3°,4°,5°,6°。

图13 不同接触倾角下的圆柱体与冰层的位置关系Fig.13 The positional relationship between the cylinder and the ice layer under different contact angles
选取θ=4°时冰层破裂过程以及突破载荷进行分析,如图14和图15所示。当圆柱体上升距离在A阶段时,圆柱体与冰层接触,突破载荷逐渐增加,由于圆柱体与冰层存在夹角,突破载荷未与接触倾角为0°时,一样成线性增加。当圆柱体继续上升至0.001 02 m时,冰层上表面形成初始裂纹,见图14(a),突破载荷会突然下降。当圆柱体上升距离在B阶段时,由于圆柱体上升高度以及接触面积的增加,突破载荷持续增加,但在此过程中由于存在径向裂纹的逐渐生长,所以突破载荷会发生卸载现象,产生波动。当圆柱体上升距离到达0.002 25 m时,突破载荷到达最大值,但之后突破载荷会突然下降,这是由于圆柱体冰层下表面发生破裂形成裂纹,见图14(b)。当圆柱体上升距离在C阶段时,突破载荷会持续振荡一段时间,这是由于随着圆柱体上升,圆柱体与冰层接触加深,冰层下表面的破裂范围扩大。当圆柱体上升距离到达0.005 55 m时,突破载荷下降至0左右,冰板被圆柱体抬起,形成半圆形冰层断裂,见图14(c)。

图14 当θ=4°时冰层破裂过程Fig.14 Ice layer fracture process at θ=4°

图15 当θ=4°时冰层突破载荷Fig.15 Ice layer breakthrough load at θ=4°
圆柱体不同接触倾角下冰层突破载荷和极值,分别如图16和图17所示。由图16和图17可知:当θ为1°,2°,3°时,突破载荷极值相差不大且极值较大;但当θ达到4°时,突破载荷的极值会发生明显下降。在圆柱体上升距离到达0.001 m之前,圆柱体与冰层初始接触过程中,突破载荷曲线几乎完全相同,但随着圆柱体继续上升,突破载荷变化趋势会产生变化:在θ为1°,2°,3°时,突破载荷增加到较高程度;而在θ为4°,5°时,突破载荷没有明显升高。这说明不同接触倾角下的圆柱体与冰层初始接触时,虽然不会对冰层上表面的裂纹萌生过程产生较大影响,但会对冰层下表面的破碎以及裂纹的生成产生较大影响,较大接触倾角下会导致冰层下表面的破碎以及裂纹产生较早,这主要是因为较大倾角会使冰层下表面破裂前受到较长时间集中载荷的作用,使冰层下表面应力迅速增加,冰层下表面较快发生破裂,导致冰层与圆柱表面接触不充分,突破载荷降低。同时,由于集中载荷的作用θ为3°,4°,5°时冰层破裂前的圆柱体上升距离相较于θ为1°,2°时有明显的减少,但在θ为6°时,冰层破裂前的圆柱体上升距离最长,冰层与圆柱体之间的持续作用最久,这主要是因为过大的接触倾角使冰层下表面破裂加剧,圆柱体使其周围的冰层先发生断裂,但随着圆柱体的继续上升,圆柱体与冰层的接触面积增加,冰层又会被圆柱体抬起发生半圆形断裂。

图16 圆柱体不同接触倾角下冰层突破载荷Fig.16 Ice breakthrough load under different contact angles of cylinder
不同接触倾角下的冰层破裂现象,如图18所示。由图18可知:在θ为0°时,冰层破裂会发生在圆柱体周围并形成碎冰堆;而在θ为2°,4°时,冰层会发生半圆形的冰层断裂;但在θ为4°时,冰层下表面较快发生破裂生成裂纹,冰层半圆形断裂范围减少;当θ为6°时,由于接触倾角过大,圆柱体周围的冰层随圆柱上升会先发生破裂随后由于接触面积的增加再发生半圆形断裂。这说明不同大小的接触倾角会使冰层垂向载荷作用下的冰层破裂模式发生较大改变。
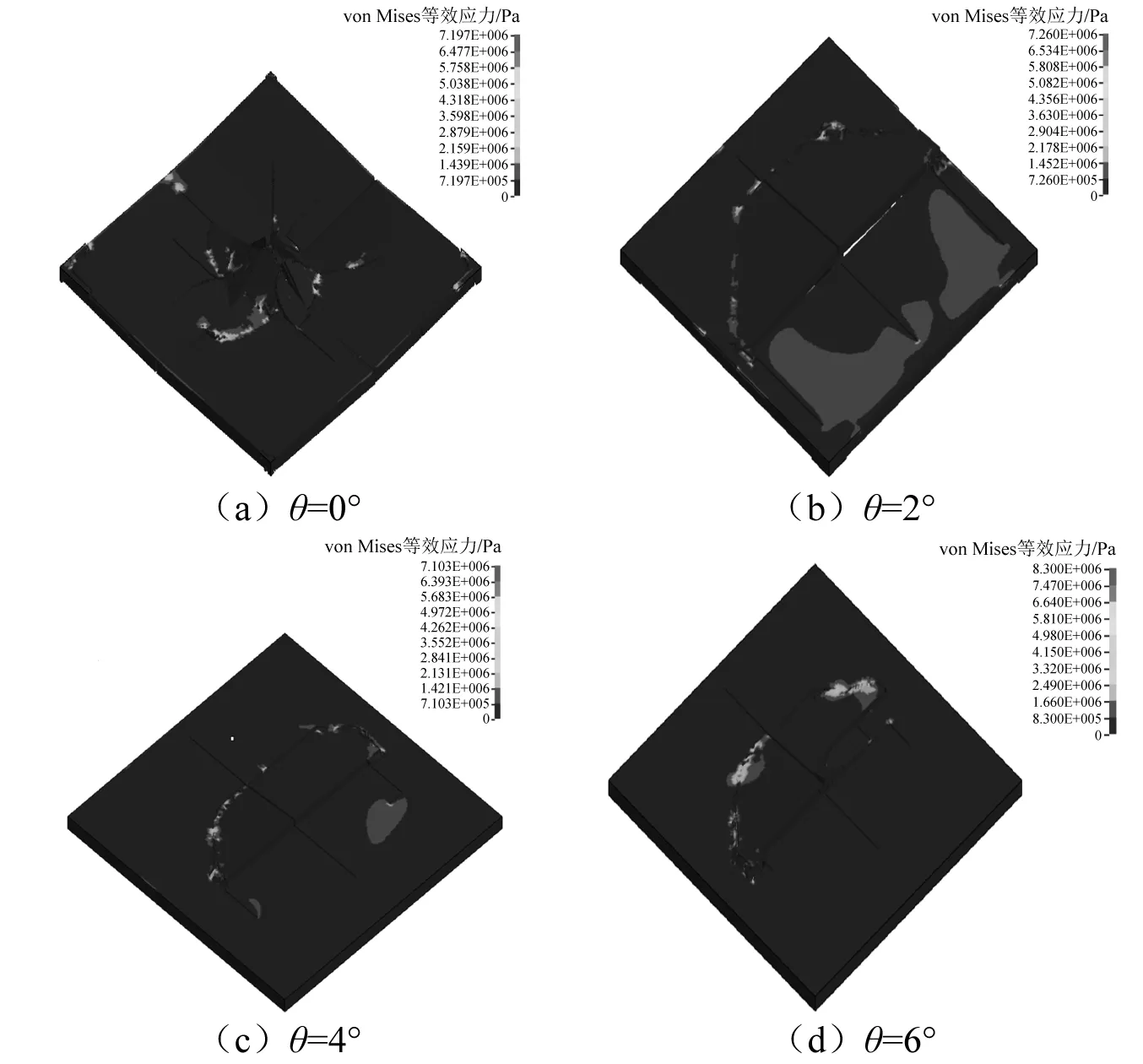
图18 不同接触倾角下冰层破裂现象Fig.18 The phenomenon of ice fracture at different contact angles
4 结 论
本文基于LS-DYNA软件,系统研究了冰层在垂向载荷作用下的破裂过程以及不同工况参数对破裂过程的影响,根据数值模拟结果得到如下结论:
(1) 开展了四点弯曲试验的数值模拟,通过与试验以及SPH法的结果与现象进行对比,验证了所选冰本构模型的可行性。
(2) 冰层在垂向载荷作用下的破裂过程会伴随着径向裂纹和周向裂纹的产生,但裂纹产生时不会导致冰层瞬间断裂,裂纹萌生时的突破载荷小于冰层最终断裂时的突破载荷。
(3) 在冰厚与圆柱体上升速度相同的情况下,均匀载荷破坏范围要大于集中载荷,但集中载荷作用下的冰层相较于均布载荷下更快到达最大抗拉应力,冰层更容易破裂。
(4) 圆柱体上升速度增大会导致圆柱体与冰层之间的相互作用更加激烈,突破载荷变化曲线会发生较大变化,无明显弹性变形阶段,冰层破裂前圆柱体相同上升距离内突破载荷和装载卸载现象会出现明显增加。
(5) 突破载荷极值大小不会随圆柱体上升速度的增大而一直增加,会出现拐点,这是因为较低的上升速度会使冰层破裂得较晚,突破载荷随圆柱上升距离增大而持续增加,最终导致极值较大。
(6) 冰层破裂现象会随接触倾角的增加发生明显变化。当θ为0°时,圆柱体周围冰层会发生破裂形成碎冰堆;当θ较小时,冰层发生半圆形断裂;随着接触倾角的增加,会使冰层下表面破裂发生较早,冰层断裂范围减少;过高的接触倾角会增加圆柱体与冰层之间的相互作用时间,使冰层破裂现象更加复杂。
(7) 该文章的研究工作主要关注冰层在垂直载荷作用下的破坏过程和突破载荷,还没有考虑水的影响。因此,在未来工作中会重点研究冰水结构物三相耦合的作用。

