基于实测动应力分析的车轴台架试验谱编制

王文静，闫瑞国，丁 然，梁韵琪，李忠文

（1.北京交通大学 机械与电子控制工程学院，北京 100044；2.中车青岛四方机车车辆股份有限公司，山东 青岛 266111）

在日常检修和维护中，往往发现车轴表面存在划痕、擦伤、冲击缺陷等损伤［1−3］，严重时造成车轴的失效断裂，引发列车脱轨或倾覆等事故的发生［4−8］。因此，基于“损伤容限”理念的定期无损探伤成为保证车轴服役安全的重要屏障。车轴探伤周期与无损检测技术的可靠性、材料的裂纹扩展行为、服役动应力等因素密切相关［9］。服役动应力与车轴损伤呈幂次关系，且与我国动车组复杂多样的运行条件相关。准确获得车轴动应力以及编制可反映实际运用状态的车轴应力谱和车轴台架试验谱，是确定合理、科学的车轴探伤周期的关键。

Filippini 等［10］采用直曲线工况下的时速600 km 车轴应力谱进行循环加载，测试变幅加载情况下车轴试样的疲劳性能；Náhlík 等［11］采用测试得到的36 级车轴应力谱进行车轴的剩余寿命计算；Zerbst等［7，12］由5.73 km 测试数据得到直曲线工况下的11 级载荷谱；Hu 等［13］使用在京沪高铁上的848 km 测试数据得到8 级载荷谱，进行S38C 材质车轴的寿命评估。然而，通过短距离测试得到的车轴应力谱和载荷谱，往往不能涵盖车轴实际运行过程中所承受的最大应力，不宜直接使用，因此需要明确车轴在长周期运营情况下的应力状态。

Beretta 等［14−17］采用线性放大和威布尔分布拟合的方法进行载荷谱外推，并进行EA4T材质全尺寸车轴的裂纹扩展试验；Luke等［18−19］将线性外推应力谱简化为5 级后进行变幅载荷裂纹扩展速率试验和不同初始缺陷下的疲劳寿命试验；Wu 等［20］使用线性外推应力谱进行数值分析，得到车轴不同部位的应力响应；陈道云等［21］使用扩展因子法对轴箱加速度载荷谱进行外推。但威布尔分布与线性外推方法仅对发生次数较多的载荷具有良好的拟合效果，对应力极值（应力谱中出现的最大应力）很难准确推导；扩展因子法只能用于标准累积频次谱的外推，由于标准谱的参数较少、形状单一，很难用于拟合线路的实测结果［22］。应力极值的差异对车轴的寿命有着重要影响［23］，因此构建台架试验谱时需对极值区域的应力分布着重关注。

本文基于长距离线路动应力测试结果，在分析车轴动应力影响因素的基础上，结合极值理论外推得到不同运行里程下的车轴应力谱；对外推应力谱进行分区后，确立等损伤的车轴台架试验谱，开展含弦形缺陷车轴台架疲劳试验，试验结果可为车轴磁粉探伤周期优化提供支撑。

1 车轴动应力测试

测试对象为动车组车轴，其材质为表面经过高频淬火硬化处理的S38C 中碳钢，具有外强内韧的梯度特性［24］。通过有限元计算，得到直线工况下车轴应力分布如图1所示。从图1可以看出：轮座内外侧截面、齿轮箱座内侧截面为车轴应力较大的截面。

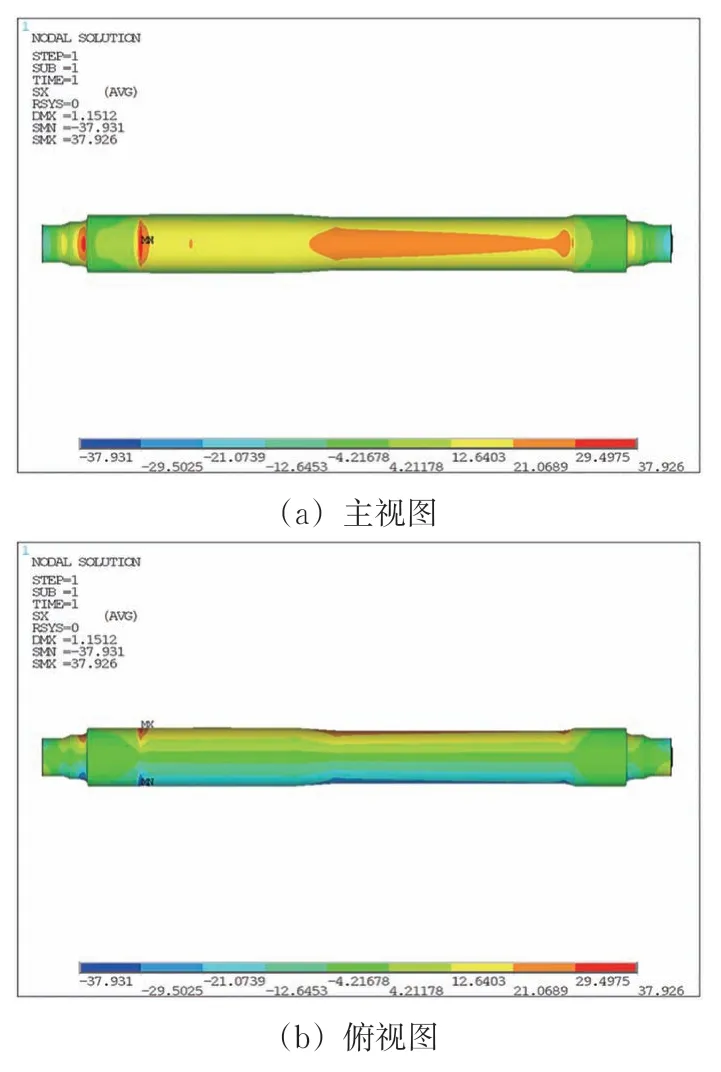
图1 直线工况下车轴应力分布

依据分析结果确定应力测点，选取的测试截面如图2所示。图中：A 截面和H 截面为轴颈内侧截面；B 截面和G 截面为轮座外侧截面；C 截面为车轴卸荷槽截面；F 截面为轮座内侧截面；E 截面为车轴轴身截面。

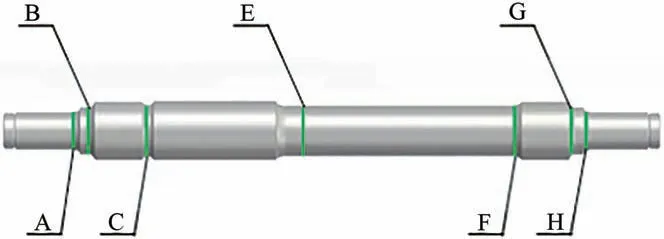
图2 车轴应力测点分布

测试相关信息如下。

试验工况：直线工况、曲线工况、道岔工况等；

试验里程：11 000 km；

试验速度级：200～250 km·h−1；

采样频率：5 000 Hz。

试验中使用陀螺仪传感器采集车身垂向、横向和纵向角速度，使用GPS 信号测试仪确定动车组运行轨迹和行驶速度。

选取同一交路下动车组运行时各截面数据进行分析，得到各截面应力谱如图3所示。从图3可以看出：B 截面和G 截面作为对称截面，它们的最高频次应力相同；A 截面最高频次应力最小，B 截面和G 截面最高频次应力最大，约为A 截面的1.78倍，F截面最高频次应力次之，约为A截面的1.48倍；因轮座内外侧截面处于车轴的过渡圆弧处，具有不同程度的应力集中，故B 截面、G 截面和F 截面的应力较大。

图3 车轴各截面应力谱

2 车轴动应力影响因素

为明确在不同应力谱下截面的损伤情况，使用式（1）对损伤进行计算。

式中：D为损伤值；σi为第i级应力谱的应力；Ni为第i级应力谱的循环周次；C和m为S-N曲线参数，本文研究对象的C值为1.75×1030，m值为9［25］。

由式（1）和图3可得B 截面损伤为所有测试截面中最高，因此后续分析针对B截面进行。

2.1 车辆载重

动车组在运行过程中，车轴的动应力与载重相关。满载状态（定员85 人）和空载状态下B 截面应力谱对比（满载状态载重约为空载状态下的1.17 倍）如图4所示。从图4可以看出：空载状态下B 截面最高频次应力为30.6 MPa，应力极值为68.3 MPa；满载状态下最高频次应力为36.9 MPa，相较于空载状态增大约20.6%，应力极值为71.9 MPa，相较于空载状态增大约5.3%。

图4 不同车辆载重下B截面应力谱

2.2 线路工况

当动车组经过道岔时，会产生异常的振动，导致车轴动应力增加。运行同样里程直线、曲线、道岔工况时车轴B 截面应力谱如图5所示。从图5可以看出：曲线工况下，车轴B截面最高频次应力相较于直线工况增大约15.6%，由式（1）和图5计算的损伤约为直线工况下的3.0 倍；道岔工况下，车轴B 截面最高频次应力相较于直线工况增大约13.0%，损伤约为直线工况下的2.2倍。

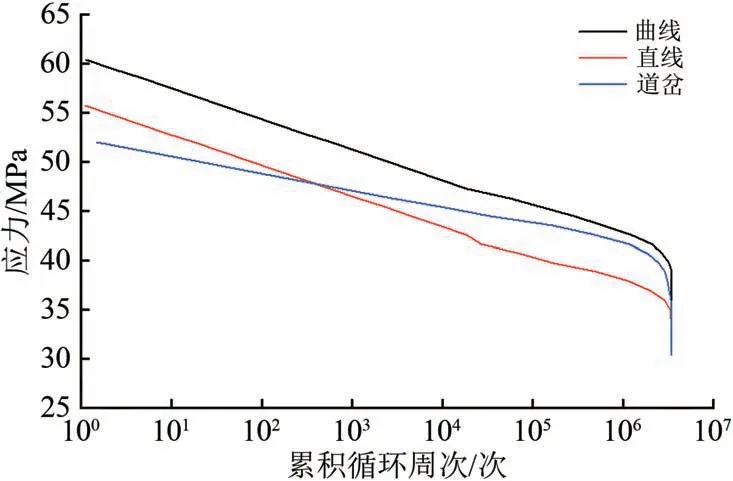
图5 不同工况下B截面应力谱

2.3 运行交路

当动车组行驶于不同交路时，由于路况不同，车轴动应力变化也有所不同。动车组在不同交路上运行同样里程时车轴B 截面应力谱如图6所示。从图6可以看出：在不同交路上运行时，车轴应力谱的最高频次应力基本一致，但应力极值具有明显差异；交路2应力极值最小，为55.1 MPa，交路3应力极值最大，为71.4 MPa，约为交路2 的1.3 倍，车轴动应力极值在动车组运行于不同交路时约有16 MPa 的波动；由式（1）和图6计算在不同交路上运行时的车轴损伤，可以发现交路5 损伤最小，交路4损伤最高，约为交路5的1.7倍。

图6 不同交路下B截面应力谱

2.4 影响因素灵敏度

车轮失圆会导致车轴应力增大，降低车轴的疲劳强度。在测试过程中，因动车组车轮状态良好，测试数据未包含车轮失圆带来的影响。而车轴应力谱外推时，应基于可反映线路实际情况的数据进行，即须在制定车轴台架试验谱时考虑车轮失圆带来的影响。基于前述测试数据最高频次应力变化的影响因素分析及文献［26−28］中关于车轮失圆影响的计算，得到各因素对车轴动应力影响的灵敏度见表1。

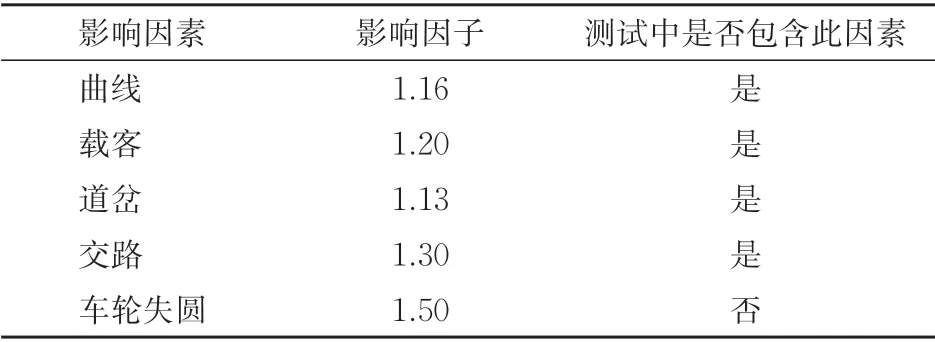
表1 影响因素灵敏度

3 应力谱极值推断

目前用于车轴应力谱推断的方式主要有线性外推和威布尔分布拟合外推等，这些方法主要侧重于描述绝大多数（高概率区）数据的行为，因此用来推断极少发生的应力极值效果欠佳；而对于车轴寿命分析，大应力循环次数对于含缺陷车轴剩余寿命具有较强的决定性作用。因此，选用基于第二极值定理（Pickands-Ballkema-de Haan定理）极值推断方法对应力谱进行推断。该定理断言随机变量的超限分布函数Fu（s）必收敛到广义帕累托分布Gξ，β（s），即

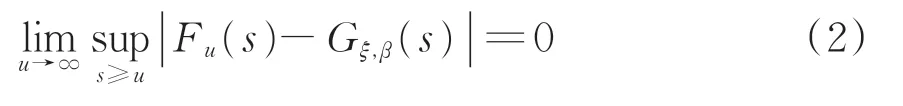
式中：u为极值区域分界点；s为应力；sup 为上确界，即最小上界；ξ和β为广义帕累托分布Gξ，β（s）的参数。

使用广义帕累托分布Gξ，β（s）拟合Fu（s），如图7（a）所示。从图7（a）可以看出：通过极大似然法可估得ξ，β的估计值分别为−0.07和4.74。由图7（a）得到的广义帕累托分布Gξ，β（s）可计算得到其概率分布曲线，如图7（b）所示，从而拟合得到极值区域各应力发生概率。

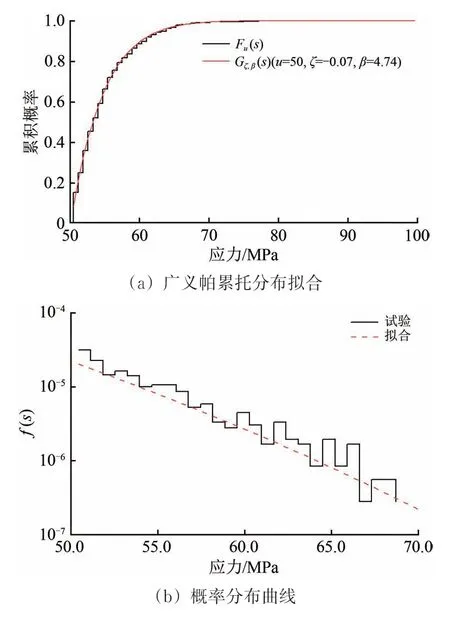
图7 B截面极值分布拟合结果

使用极值理论将B截面测试应力谱外推至不同运行里程时，应力极值随运行里程的变化如图8所示。从图8可以看出：经极值推断至不同运行里程时，B 截面应力极值随运行里程的增大逐渐增长，但增长速率逐渐减小，车轴经历的应力极值趋于稳定。

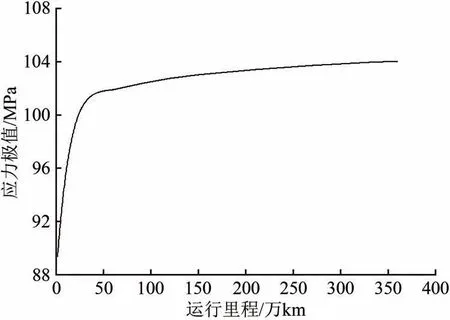
图8 不同运行里程下B截面外推应力极值

将B 截面应力谱拟合外推至240 万km 时，累积循环概率与对应的应力如图9所示。从图9可以看出：外推至240 万km 时，车轴B 截面应力谱应力极值为103 MPa。

图9 B截面240万km应力谱累计循环概率及应力分区

4 台架试验谱编制

为探究磁粉探伤周期由60 万km 延长到120 万km 的可行性，考虑2 倍的安全余量，选取外推至240 万km 的应力谱进行试验谱编制。当动车组运行240 万km 时，车轴需经历约8.4×108次载荷循环。试验台加载频率约为18～20 Hz，难以在短时间内完成8.4×108次的加载，钢的超高周疲劳S-N曲线往往为阶梯状或连续下降形［29］，因此将试验谱设定为108次，在保留超高周疲劳特性的同时缩短试验时间。

进行疲劳试验时，不同的载荷次序会影响被测对象的疲劳寿命［30］，因此在台架试验中需考虑载荷次序的影响。将240 万km 外推应力谱累积循环概率分布划分为3个区域，分别为极值应力区、过渡应力区和最高频次应力区。将用于应力极值外推的区域定义为极值应力区，应力谱中最高频次应力对应的区域定义为最高频次应力区，最高频次应力区与极值应力区之间的区域定义为过渡应力区，各应力区域划分如图9所示。

在外推应力谱划分的基础上，建立3 级台架试验谱。3 级台架试验谱分别对应极值应力区，过渡应力区和高频次应力区。台架试验谱中最高级应力为应力极值，其应力频次为应力谱中极值应力区应力总频次；最低级应力使用最高频次应力值，保证其应力频次在应力谱中占比不变；过渡应力频次由试验谱总频次减去极值应力与最高频次应力的循环周次所得到。结合材料S-N曲线，采用Miner 法则，按照式（3）计算得到车轴台架试验谱过渡应力σmid为

式中：σmax为台架试验谱中最高级应力；Nmax为最高级应力的循环周次；Nmid为台架试验谱中过渡应力的循环周次；σmin为台架试验谱中的最低级应力；Nmin为台架试验谱中的最低级应力的循环周次。

考虑到可能出现的车轮失圆等因素，将安全系数定为1.50，得到等效3 级谱（3 级应力及其循环周次分别为：55.5 MPa，9 000 万次；86.0 MPa，995 万次；154.0 MPa，5 万次）。同时，考虑到低→高、高→低、低→高→低、高→低→高等加载次序带来的影响，将108次的3 级谱划分为10 个模块，每个模块加载107次，加载模块如图10所示。

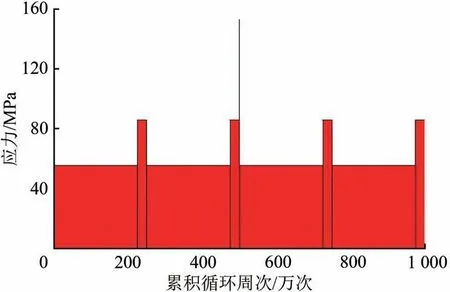
图10 107循环次数加载模块示意图

5 台架试验谱应用

5.1 考察截面及初始缺陷选取

由于车轴试验台试样的特殊安装与加载方式，车轴轮座外侧截面处于约束区域，不能作为考察截面，因此，选用除轮座外侧截面外应力最大截面（轮座内侧截面）作为考察截面。同时，为起到保守评估的效果，使用图10中由车轴B 截面应力谱外推得到的台架试验谱进行加载。

由于外物击打对车轴性能具有较大影响［31−32］。对车轴击打伤进行调研分析，得到在运用过程中击打伤深度分布：车轴在运用过程中产生的击打伤深度有68.75%在0.3 mm 以内，且所有击打伤深度均小于1.0 mm。

为探究缺陷深度和形貌对车轴应力所带来的影响，使用有限元分析得到不同形貌和深度缺陷的应力集中系数如图11所示。从图11可以看出：在不同缺陷形貌中，弦形缺陷的应力集中系数最大。因此，在车轴上预制弦形人工缺陷模拟可能出现的击打伤。

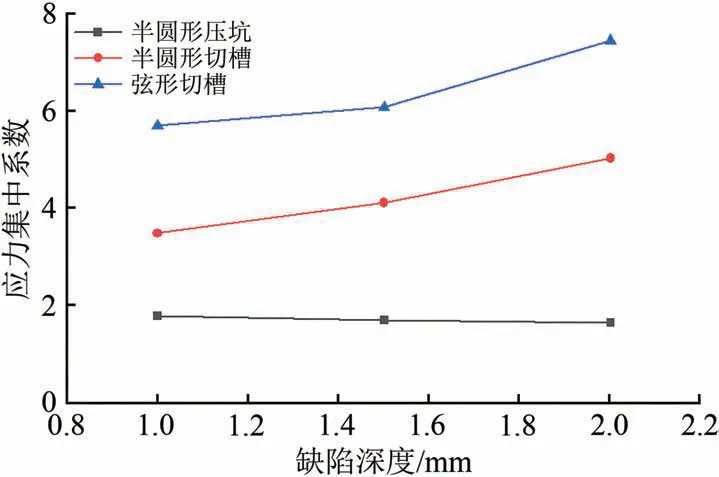
图11 不同形貌缺陷应力集中系数

考虑到在今后运行中可能会出现更加恶劣的情况，对缺陷深度进行放大，使用电火花加工方式在考察截面预制4 个2 mm 深的弦形缺陷，相邻缺陷间隔角度为90°，以避免试验结果的偶然性。缺陷预制位置和预制情况如图12所示。

图12 车轴缺陷预制情况

5.2 车轴疲劳试验

对预制人工缺陷后的车轴进行磁粉探伤，确认车轴初始状态，按现行工艺将试验车轴与车轮进行装配。使用得到的台架试验谱在车轴疲劳试验台（如图13（a）所示）上进行加载，在加载过程中对缺陷所在截面的应力和缺陷长度进行监控（监控结果如图13（c）和图13（d）所示）。108循环周次台架试验谱加载完成后对4 处缺陷进行磁粉探伤，车轴缺陷表面未见裂纹萌生。将缺陷取样，使用CT 扫描对缺陷前缘进行观测，结果如图14所示。从图14可以看出：在可反映240 万km 线路实际影响的台架试验谱加载下，2 mm 深度弦形缺陷根部与表面均无微裂纹萌生，该结果为车轴磁粉探伤周期优化提供了支撑。

图13 车轴试验台应力控制过程

图14 CT扫描结果

6 结 论

（1）S38C 材质动力车轴的轮座外侧圆弧截面因直径较小，应力最大，轮座内侧圆弧截面应力次之。

（2）满载工况下，车轴截面应力值为空载状态的1.2 倍；在满载运行过程中，车轴最大应力截面应力极值随线路变化约有16 MPa 的波动；相较于直线工况，曲线和道岔工况下，最大应力截面的最高频次应力分别增大约15.6%和13.0%。

（3）使用极值理论将测试应力谱外推至不同里程时，应力极值逐渐增大，但其增长速率逐渐变缓，车轴截面应力谱应力极值逐渐收敛，外推得到运行240万km时的车轴应力谱累积循环概率。

（4）考虑车轴疲劳试验台的加载特性和载荷次序带来的影响以及动应力影响因素，根据材料S-N曲线，结合Miner 法则，等效得到适用于台架疲劳试验的3 级应力谱，并开展了全尺寸含弦形缺陷车轴台架疲劳试验，试验结果为车轴磁粉探伤周期优化提供了支撑。