自然曲线井眼轨道设计模型及反演求解方法

刘珊珊，赵亦朋，王小秋，汪志明

(1.中国石油大学(北京)石油工程学院，北京 102249；2.中国石油集团 工程技术研究院有限公司，北京 102200)

引 言

在钻井轨道设计中，经常将井眼轨道假设为某些简单的空间曲线，如空间圆弧等，这些模型形式简单，求解方便，因此应用广泛，能够解决大多数的井眼轨道设计问题[1-5]。然而针对造斜同时伴随方位变化的钻井轨道，需要更复杂的轨道模型。此外，当钻井与设计轨迹不一致时，使用空间圆弧等模型不是实现自动化钻井的最佳选择，由于其不连续性，导致钻柱上产生显著的应力，扭矩和阻力增加，钻井所需的能量也相应增加。自然曲线井眼轨迹在钻柱上的应力、扭矩和阻力相对圆弧轨迹要小，能量成本明显低于圆弧轨迹，从而降低了钻井能耗。不同的轨迹模型在同一曲线上产生不同的能量消耗，有研究表明自然曲线法为最佳的轨道模型[6-9]。知名的钻井轨道设计软件Compass中的Build/Turn设计模型，即采用自然曲线模型。

鲁港等人[10]对自然曲线模型的数值计算进行了研究，给出了自然曲线模型在给定造斜率和转向率的条件下，用泰勒展开求解的井段ΔX、ΔY和ΔZ的通用求解方法，未涉及约束条件下的模型反演。何树山等人[11-12]给出了一个模型反演的基本流程，但是其初值的选择不能保证在大斜度的情况下迭代收敛，难以保证算法的稳定性。

本文在上述研究的基础上，针对自然曲线轨道模型定点和垂深对齐问题的反演计算，提出了新的计算流程，并针对垂深对齐问题提出了新的初值选择方法，通过多个算例进行验算，较商业化软件具有更高的计算精度。

1 设计模型

自然曲线法描述的是一个空间三维曲线(图1),该曲线假设井段内的井斜变化率和方位变化率分别为常数[6]，则

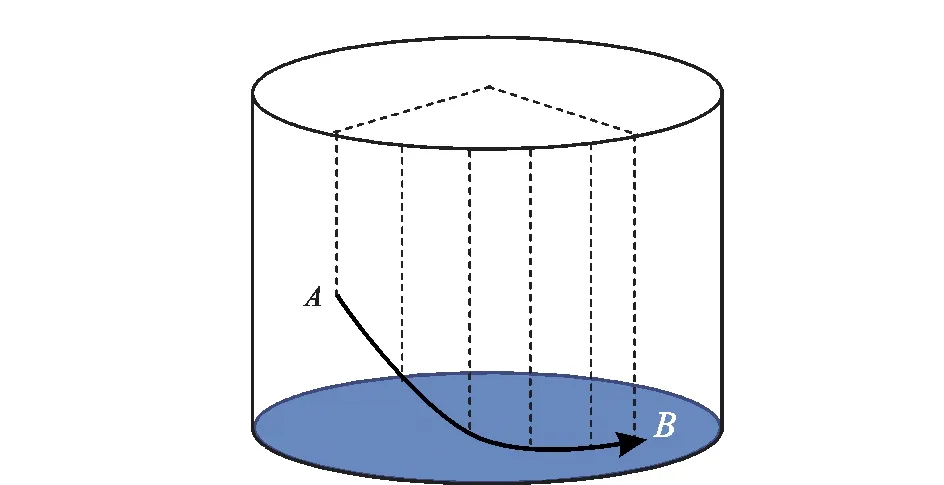
图1 自然曲线示意图

Δα=αB-αA，

(1)

Δφ=φB-φA，

(2)

ΔL=LA-LB，

(3)

(4)

(5)

式中：(LA,αA,φA)及(LB,αB,φB)分别为井段上、下两个测点的测深、井斜角和方位角；Kα为井斜角变化率(造斜率)；Kφ为方位角变化率(转向率)。

1.1 轨道参数计算

自然曲线模型，从A点以造斜率Kα和转向率Kφ钻进ΔL长度的井段到达B点，各个轨道参数的计算分别为[6]

αB=αA+KαΔL；

(6)

φB=φA+KφΔL；

(7)

(8)

(9)

(10)

(11)

式中：ΔN、ΔE、ΔZ分别为井段在北、东以及垂深方向的增量；ΔS为轨道在水平面上投影的曲线长度。式(8)—(11)中，对于Kα=0和Kφ=0的特殊情况参见文献[6]。

鲁港等人[10]通过定义一个辅助函数λ(x)对式(8)—(11)进行简化得

(12)

对式(12)在x=0处进行泰勒展开得

(13)

式(13)中第5、6两项为高阶小量，工程上取前4项即可满足计算精度要求。借助函数λ(x)，可使用

(14)

(15)

(16)

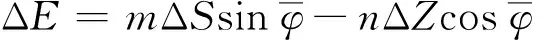
(17)

统一形式计算。其中，

(18)

a=λ(Δα+Δφ),b=λ(Δα-Δφ),c=λ(Δα)(其中Δα=αB-αA，Δφ=φB-φA)，

(19)

(20)

1.2 约束条件下的模型反演问题

本文将探讨两种约束条件下的反演问题：

(1)定点问题：给定ΔN、ΔE和ΔZ，反演求解ΔL、Kα和Kφ。

(2)垂深对齐问题：给定ΔN、ΔE和ΔZ，并要求曲线段终点到达指定的垂深后，稳斜到目标点，反演求解造斜段长度ΔL1、稳斜段长度ΔL2、Kα和Kφ。

两种反演问题如图2、图3所示。现有研究中，很少说明自然曲线模型的反演求解算法，本文针对这两种问题，给出详细稳定的求解算法。

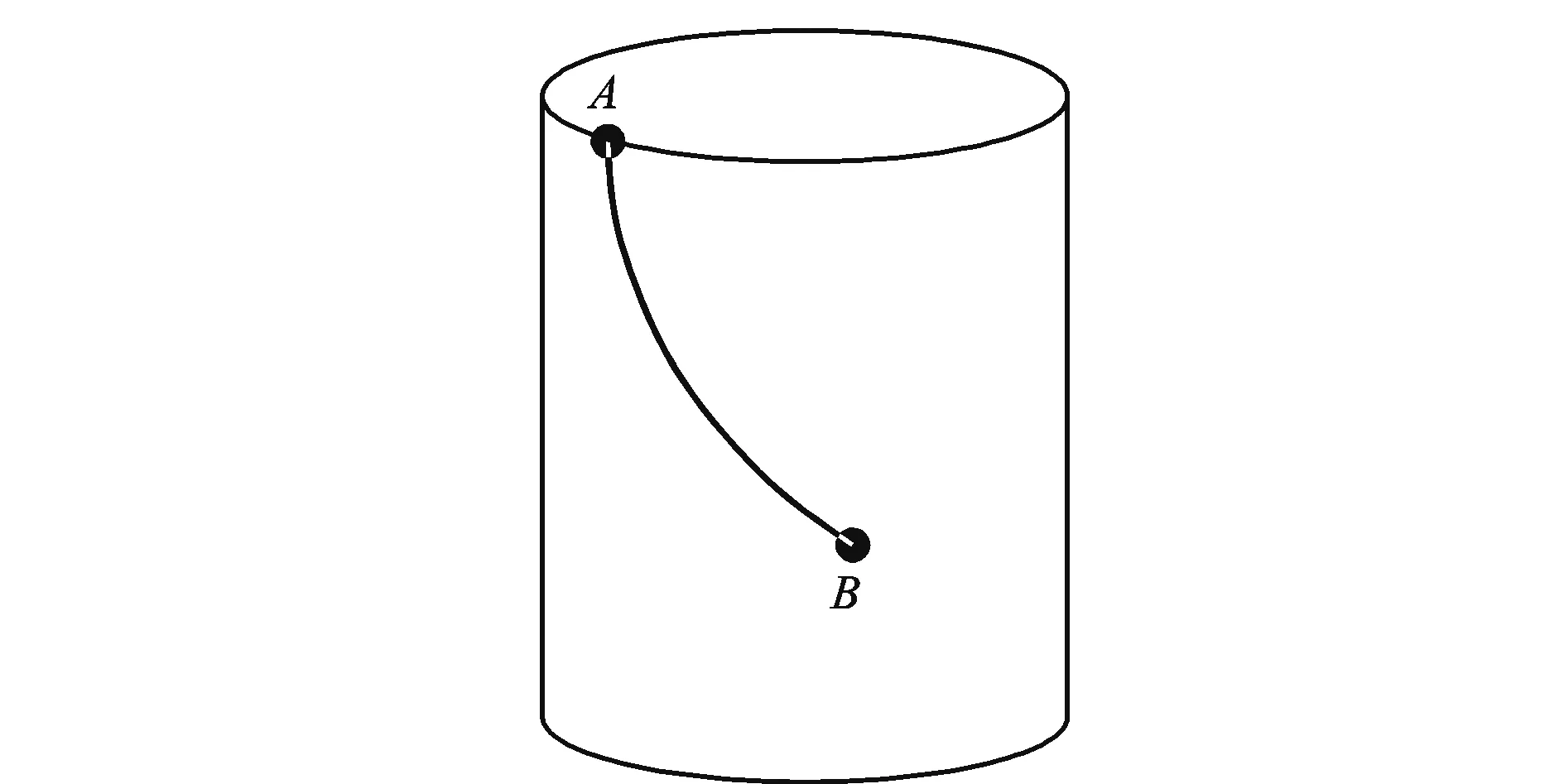
图2 第一种约束条件

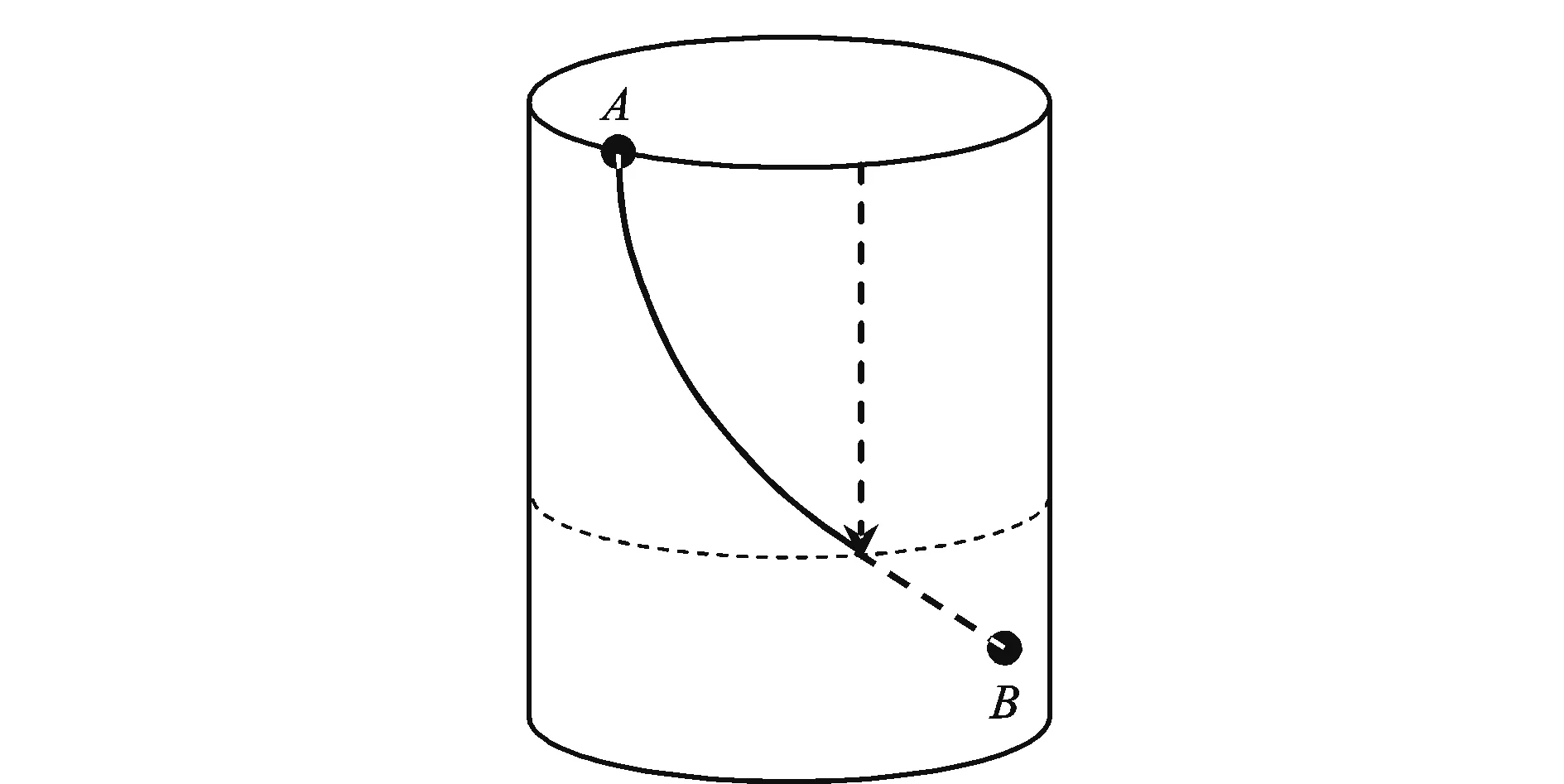
图3 第二种约束条件

2 定点问题的求解方法

设井段起始点和终止点为A和B，已知条件为(LA,αA,φA,NA,EA,ZA)和(NB,EB,ZB)。模型求解流程如下：

(1)计算AB连线的斜率

(21)

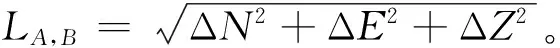
(22)

若αA,B>0则该井段为增斜，若αA,B<0则该井段为降斜，若αA,B=0则为稳斜。

(2)给αB一个初值，可取为[11]

(23)

根据A点方位角和坐标偏移量，求解方位变化方向和方位角初值。根据φA建立变换矩阵M，对ΔN和ΔE进行变换，确定沿方位角φA方向的坐标增量以及方位角的变化初值Δφ0。

(24)

(25)

(26)

(4)计算井段长度ΔL

(27)

(5)求解方位角φB

根据式(8)、(9)可得

(28)

式(8)中，只有φB一个未知数，但由于公式极为复杂，无法得到φB的解析表达式，通过计算分析该式在φB的临域范围内函数具有单调性。因此，可以使用牛顿迭代法，快速计算φB的值。对式(28)求导得

(29)

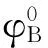
(30)

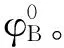
需要注意的是，在式(29)、(30)中，当出现两个分子项|Δα±Δφ|→0的情况，由于计算机的浮点计算误差，这时的计算结果不准确，当其等于零时，将会出现除零的错误。在迭代的过程中，这一情况难以避免，因此算法必须考虑|Δα±Δφ|→0的极限问题，在此临域内，用极限代替计算，避免计算错误的发生。

(6)求解井斜角αB

根据式(8)、式(9)，使用ΔN和ΔE均可计算ΔL，考虑到数值计算有一定误差，浮点运算数越小，误差越大，可根据ΔN和ΔE绝对值的大小，选择绝对值较大的项计算当前的ΔL。根据式(15)推导得

(31)

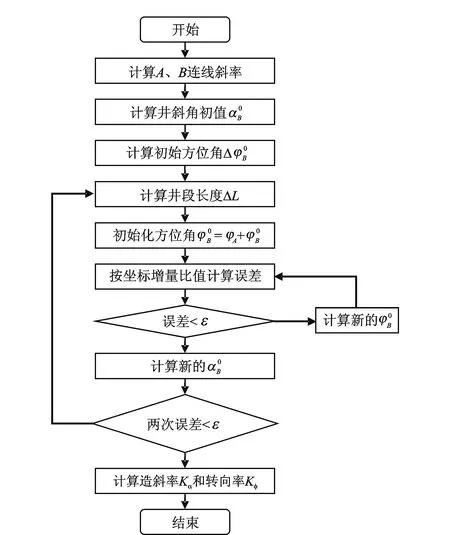
图4 定点问题计算流程图

3 垂深对齐问题的求解方法

该问题分为两个井段(图3)，第一个井段是自然曲线段，通过在该段造斜和转向，在指定的垂深(TVD)对齐到目标点，并由此点开始稳斜到目标点，即第二个井段为直线段。根据自然曲线段和直线段的坐标偏移公式，建立坐标增量公式

ΔL2sinαBcosφB；

(32)

ΔL2sinαBsinφB；

(33)

(34)

(35)

式中：ΔN、ΔE、ΔZ1、ΔZ2、αA、φA为已知参数；曲线段长度ΔL1、直线段长度ΔL2、直线段井斜角αB和直线段方位角φB为未知参数。

该问题的求解与定点问题的求解思路类似，但因为存在直线段，所以稍微有些复杂。具体计算流程如图4(为叙述的一致性，仍假设首末两点为A、B)。

(1)计算AB连线的斜率

同定点问题(1)。

(2)给定αB初值

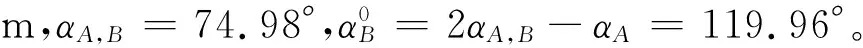
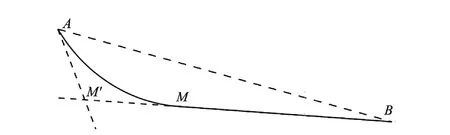
图5 垂深对齐的初值问题

通过观察，初值应在AB连线和AM′连线之间，取∠BAM′的角平分线作为初值，即

(36)

同定点问题(3)。

(4)计算曲线段长度ΔL1

(37)

(5)求解方位角φB

直线段的斜率

(38)

整理可得

f(φB)=sinφB(ΔN-ΔN1)-cosφB(ΔE-ΔE1)=0。

(39)

该函数在求解区间的图形如图6所示。虽然该区域内只有一个解，但函数并不保持单调性，有间断，因此不能采用迭代法求解，只能按照方位角变化方向，使用搜索算法求解。

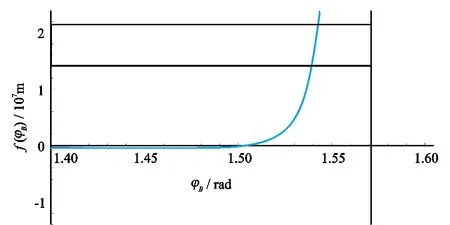
图6 式(39)曲线形态

(6)求解井斜角αB

根据式(32)和式(33)，得

f(αB)=(ΔN1+ΔN2-ΔN)2+(ΔE1+ΔE2-

ΔE)2=0。

(40)

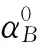
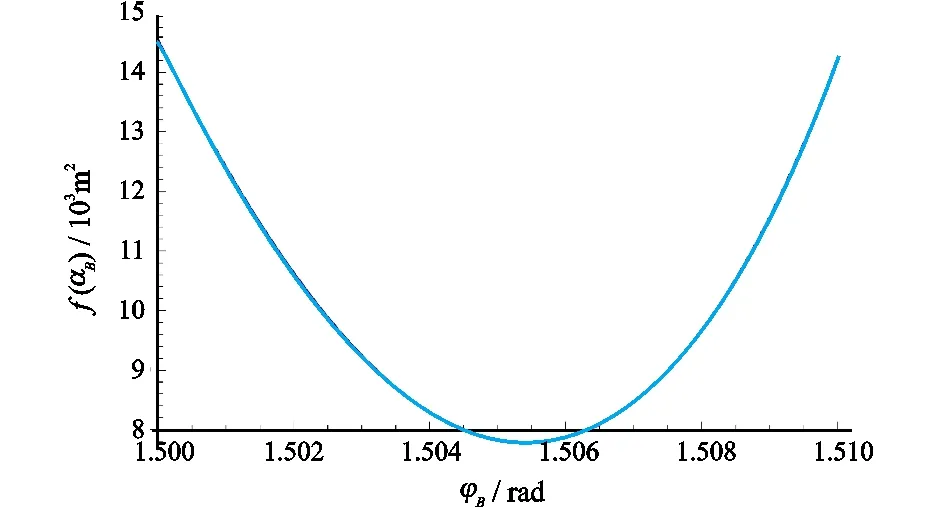
图临域内的函数值

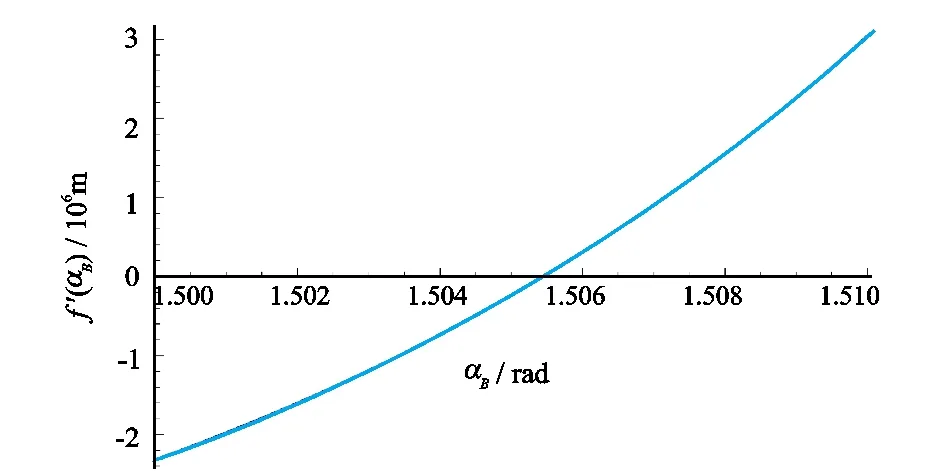
图临域内的导数值

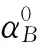
f′(αB)=2(ΔN1+ΔN2-ΔN)(ΔN1+ΔN2)′+2(ΔE1+ΔE2-ΔE)(ΔE1+ΔE2)′=0；

(41)

(ΔN1+ΔN2)′=

(42)

(ΔE1+ΔE2)′=

(43)

4 计算实例

根据上述两种条件下的求解方法，编制了相应的软件，以下给出两种不同类型问题的计算实例，由于现有文献中提出的初始井斜角计算方法不适用于大斜度垂深对齐问题，因此，专门提供了一个大斜度算例，用以验证本文算法的适用性，同时与知名的商业软件Compass进行对比。

(1)算例1 定点问题

起始点A：测深=1 000 m,井斜角=30°，方位角=0°，垂深=1 000 m，北坐标=0 m，东坐标=0 m；靶点B点：垂深=1 100 m，北坐标=100 m，东坐标=50 m，本文与Compass软件计算结果对比见表1。

表1 算例1计算结果

(2)算例2 垂深对齐问题

起始点A：测深=1 000 m,井斜角=30°，方位角=0°，垂深=1 000 m，北坐标=0 m，东坐标=0 m；造斜段末点垂深=1 080 m；靶点B点，垂深=1 120 m，北坐标=100 m，东坐标=50 m，本文与Compass软件计算结果见表2。

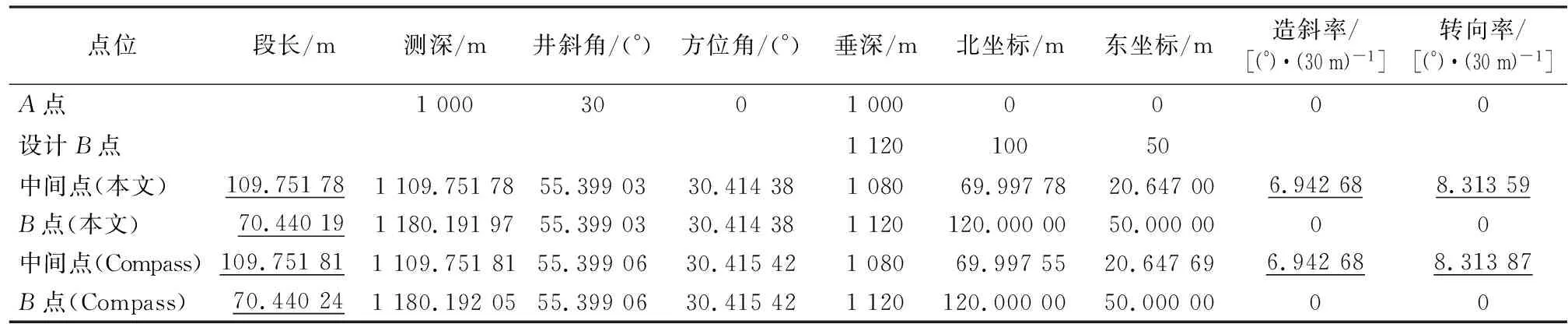
表2 算例2计算结果

(3)算例3 垂深对齐问题(大斜度井)

起始点A：测深=1 000 m,井斜角=30°，方位角=0°，垂深=1 000 m，北坐标=0 m，东坐标=0 m；造斜段末点垂深=1 100 m；靶点B点，垂深=1 120 m，北坐标=400 m，东坐标=200 m，本文与Compass软件计算结果见表3。

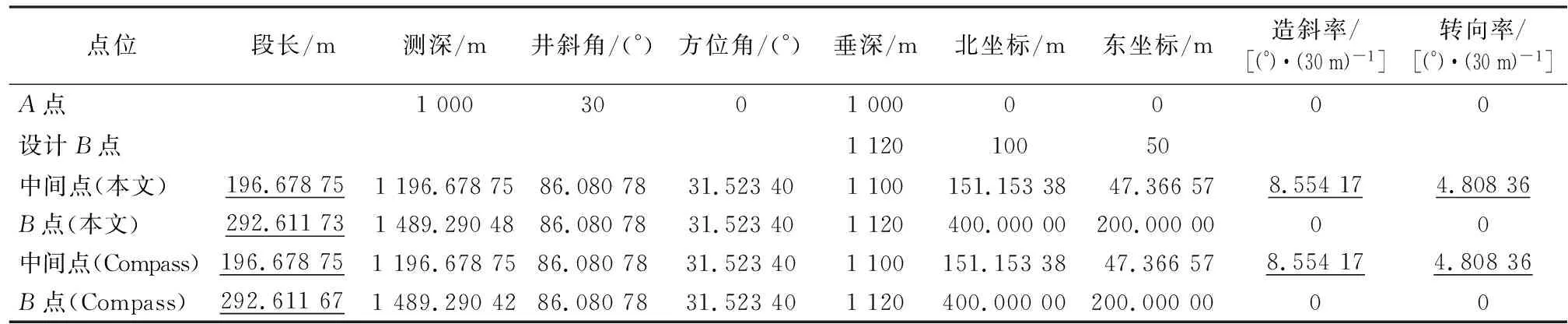
表3 算例3计算结果

表1—表3中，下划线的数据为计算出的关键参数，分别为段长、造斜率和转向率，根据这些关键参数和垂深约束条件，计算出每个井段的北坐标和东坐标等参数。

由表1可见，本文算法的最大误差为1.0×10-5，Compass计算的最大误差为1.13×10-3，本文算法精度高于Compass。由表2、表3可见，本文算法与Compass计算的结果均较为精确，在1.0×10-5数量级没有误差，可认为精度一致。综上所述，针对定点问题本文算法计算精度高于Compass计算精度，针对垂深对齐问题精度一致。当然，从工程角度来看，两者计算结果均能满足需求。

需要指出的是，前文给出了严格的数学公式，有利于理解问题的本质。但是在实际的软件中，完全采用这些公式，特别是导数公式，往往使程序过于繁琐，因此在具体实现过程中，可以使用式(14)—(17)计算函数及差商实现求解，同样可以达到收敛的效果，简化程序的编写。

5 结 论

造斜段伴随方位变化的自然曲线模型，是一种非常规的三维钻井轨道设计模型，可减少钻井摩阻。本文详细讨论了两种约束条件下的模型反演求解问题，分别给出了两种问题的求解流程。计算实例证明，针对定点问题本文算法计算精度高于Compass计算精度，针对垂深对齐问题精度一致。由于商业软件价格昂贵，并且每年需缴纳大量维护费用，因此研究国产替代软件非常必要，该算法应用于钻井工程设计软件，对于实现国产软件替代进口软件具有重要的意义。