基于CSAGA-LSSVM算法的坦克驾驶模拟训练数据分类挖掘
邓 青,薛 青,翟 凯
(1. 陆军装甲兵学院 演训中心,北京 100072; 2. 68303部队,青海 格尔木 816099)
坦克驾驶模拟训练是装甲兵掌握驾驶技能的重要途径,对提高装甲分队战场快速机动能力具有重要意义[1-2]。坦克驾驶模拟训练数据包括训练操作数据、受训人员数据等,这些数据之间蕴含着复杂的关系。传统的坦克驾驶模拟训练结果由人工进行统计分析[3],易受分析人员专业知识、个人偏好的主观影响,对训练的影响因素考虑不全,无法精确指导受训人员,也难以从这些复杂的数据中发现有价值的训练规律。为解决这一问题,提出将分类挖掘引入坦克驾驶模拟训练数据分析中,以期从中获取训练指导规律。
Robinson等[4]运用主成分分析方法对通信指挥模拟训练数据进行分析,为实施作战指挥提供支持,但需要事先提取指挥员的能力特征表示,不同场景下的概念描述比较繁杂。Cady[5]选择装甲装备模拟训练系统中的地形条件、任务样式、敌人属性等作为输入数据,运用定制的聚类算法和最小二乘法进行分析,得出杀伤力、战损率等结果与输入数据之间的关系,但算法细节没有描述。Wang等[6]采用聚类方法分析装甲兵模拟训练数据,通过发现数据分布的簇特征,去除离群值,计算车辆位置的平均值,得出中心点移动速度与各车速度之间的关系,为机动力评估提供依据,但均值计算存在有偏估计问题。邓桂龙等[7]运用关联规则方法分析某型空地作战系统模拟训练数据,提取雷达连续照射时间、打击导弹阵地种类与作战效果之间的强关联规则,辅助作战分析人员获取更多有用的知识,但生成规则的数量庞大,需要人工筛选。唐志武等[8]采集了装甲兵模拟训练系统在特殊想定条件下的交战数据,运用多变量决策树进行分析,得到机动、防护等作战能力指标的影响因素,但决策树的分叉比较繁琐。贝叶斯网络运用有向图模型来描述和计算变量之间的概率依赖关系,利用先验知识更新后验概率,但往往需要专家确定初始值[9],而坦克驾驶模拟训练数据在很多情况下无法提前确定先验概率。决策树分类具有原理简单、抗噪音强等优点[10],主要适用于小样本数据集的分类,在面对海量高维度数据时易产生无效节点。深度学习在图像识别、自然语言理解领域有着广泛运用[11],适合从高维度数据中提取特征,但由于内部的“黑盒”,对提取特征可解释性较差。最小二乘支持向量机(least squares support vector machine,LSSVM)利用核函数、特征空间等处理高维数据,实现从样本空间到特征空间的映射,具有良好的分类能力[12-13]。
坦克驾驶模拟训练数据具有时序性的特点,不能直接输入LSSVM进行分类,而要提取相应的特征后进行分类,同时LSSVM存在的超参选择难问题也需要解决。本研究在LSSVM中引入Shapelets并进行组合以提取原始数据特征,设计自适应遗传算法(adaptive genetic algorithm,AGA)实现超参数的最优选择,最终得到一个组合Shapelets的自适应遗传最小二乘支持向量机算法(combination shapelets adaptive genetic algorithm-least squares support vector machine, CSAGA-LSSVM),将其应用于坦克驾驶模拟训练操作数据分析,通过分类得到标准的驾驶操作动作集合,更好地对受训人员进行指导。
1 坦克驾驶模拟训练数据分类挖掘问题描述
坦克驾驶模拟训练数据中的知识和信息是分析决策的有效依据。对这些数据进行分类挖掘,除了具有传统意义上的分类挖掘含义外,更重要的目标是从中发现有意义的模式。
从模拟器的数据采集分系统中抽取数据集B=(B1,B2,…,Bn),将B划分为若干个不重复的记录,其中每个元组都对应相同数量的条件属性和类别属性,假设条件属性值的集合为C={C1,C2,…,Cn},类别属性值的集合为D={D1,D2,…,Dn},则分类挖掘问题为发现从C到D的映射f:C→D[14]。在此基础上,将坦克驾驶模拟训练数据分类挖掘描述如下:
假设P={P(k)|k=1,2,…,N}为坦克驾驶模拟训练数据的N维特征空间U⊂RN中所包含的非空模式集,其中任一子集族记为S={S(l)|l=1,2,…,c,1≤c≤N},若约束条件
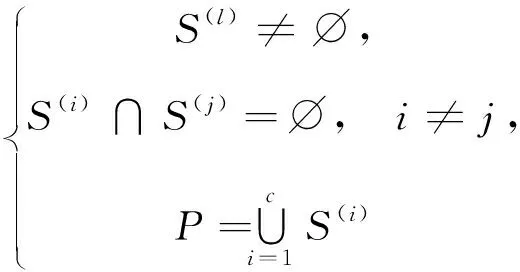
(1)
成立,则称S是对N维特征空间划分所形成的一个子类,即S为P中的一个分类。
2 CSAGA-LSSVM分类挖掘算法
TS={vt1,vt2,…,vti,…,vtn}是一个实值时间序列,其中vti为时间序列点,n为时间序列长度;记为|TS|。通常相邻时间序列点之间是等间隔的,时间序列简记为TS={v1,v2,…,vi,…,vn}。时间序列的子序列TSj,l={vtj,vtj+1,…,vtj+l-1}是一个从TS取出起始位置为j、长度为l的连续序列。m个时间序列TS组成的集合称作时间序列数据集,记为DTS={TS1,TS2,…,TSi,…,TSm},其中时间序列数据集的实例数|DTS|=m。
Shapelets是时间序列TS中能够最大程度确定该序列所属类标签的特征表示,也是最具有辨识性和可解释性的局部时序模式。一个长度为k的Shapelets={s1,s2,…,sk}是时间序列TS={v1,v2,…,vi,…,vn}的一个子序列。在时间序列分类问题中,从时间序列数据DTS集中每次学习获得的时间序列Shapelets长度并不相同。
2.1 基于关键点的Shapelets快速获取
Shapelets获取是整个分类算法的第一步,通过定义关键点筛选子序列,减少产生的候选Shapelets个数,从而快速获取Shapelets[15]。
关键点是从时间序列点内部产生的,并能够表达时间序列的主要特征和变化趋势。本研究的关键点包括时间序列的起始点、结束点、阶跃点和极值点。
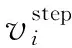
(2)
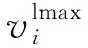
(3)
其中k是极值点附近邻域的大小。
确定关键点后,按以下步骤产生Shapelets:
1)Key为存储关键点的数组,Dsup为存储Shapelets的字典,初始化均为空。设定初始邻域k、阈值ρ。TS={v1,v2,…,vn}为一时间序列,n为时间序列长度,i=1;
2) 判断点vi是否为时间序列的起始点,若是则将点vi存入数组Key中,转步骤6);
3) 判断点vi是否满足vi-k≤vi且vi+k≤vi或vi≤vi-k且vi≤vi+k,若是则将点vi存入数组Key中,转步骤6);
4) 判断点vi是否满足(vi+1-vi)/(vi-vi-1)≥ρ,若是则将点vi存入数组Key中,转步骤6);
5) 判断点vi是否为时间序列的结束点,若是则将点vi存入数组Key中,转步骤7);
6) 结束对点vi的处理,i=i+1,转步骤2);
7) 对关键点数组Key进行遍历,按顺序依次从Key中取出两个元素构成Shapelets的两个端点,并将该Shapelets及其所在的序号存入Dsup。
2.2 组合Shapelets特征生成
通过坦克驾驶模拟器可以进行各种驾驶操作练习,对油门、离合等部件的操作有明确的先后次序和时间间隔要求,因此受训人员的驾驶动作识别属于多维时间序列分类问题。而之前获取的Shapelets由于忽略不同序列之间的操作时间、逻辑组合等关系,难以达到准确的辨识效果。因此将多个Shapelets进行组合,并加入时间间隔,以增强组合Shapelets的分类能力,并通过信息增益评价最优Shapelets组合,以提高分类的准确性。
对于长度均为n的TS1和TS2,采用欧氏距离
(4)
作为两个时间序列之间的距离,来度量两者间的差异。
对于Shapelets子序列s与TSi的距离shpdis(s,TSi),采用滑动窗口方式在TSi上生成(n-s+1)个与s等长的序列TSi,|s|,按式(4)计算距离,由动态弯曲距离比对原则取最小值作为s与TS1之间的距离度量,即:
shpdis(s,TSi)=min(dis(s,TSi,|s|)) 。
(5)
对于时间序列数据集DTS={TS1,TS2,…,TSi,…,TSm},类标签的个数为C,设某一类ci在时间序列数据集DTS中有ni个时间序列,则时间序列数据集DTS的熵表示为:
(6)
随机选择s1、s2两个Shapelets进行合取操作,按式(5)分别计算s1、s2与DTS={TS1,TS2,…,TSi,…,TSm}中每一个时间序列之间的距离。合取后的s1∧s2同时含有s1、s2的特征,则s1∧s2与TSi的距离comshpdis(s1∧s2,TSi)应取两者中较大的值进行度量:
comshpdis(s1∧s2,TSi)=max(shpdis(s1,TSi),shpdis(s2,TSi)) 。
(7)
对s1∧s2与DTS={TS1,TS2,…,TSi,…,TSm}中时间序列的距离按递增顺序存入一维数组Discshp。设定阈值δ,遍历数组Discshp元素并与δ比较,将时间序列数据集DTS分成DTSleft、DTSright两部分:
DTSleft={TSi|TSi∈DTS,Discshp[i]≤δ},
(8)
DTSright={TSi|TSi∈DTS,Discshp[i]>δ}。
(9)
通过式(6)计算DTSleft、DTSright数据集的熵,得到s1∧s2的信息增益
(10)
以对s1∧s2进行评估,并将对应的子序列加入候选组合Shapelets,记作Canshp。
为增强组合Shapelets的分类能力,参照决策树的构建思想,将Shapelets之间的时间间隔作为分类的辅助特征,减少单纯使用距离度量分为两个数据集DTSleft、DTSright所产生的分类误差。在式(5)中,通过求取s与TSi的距离最小值,找到最佳匹配初始位置记作Bpos(s,TSi),TSi(Bpos(s,TSi),Bpos(s,TSi)+s-1)表示时间序列TSi从初始位置Bpos(s,TSi)开始,长度为|s|的子序列,则有:
shpdis(s,TSi)=dis(s,TSi(Bpos(s,TSi),Bpos(s,TSi)+s-1)) 。
(11)
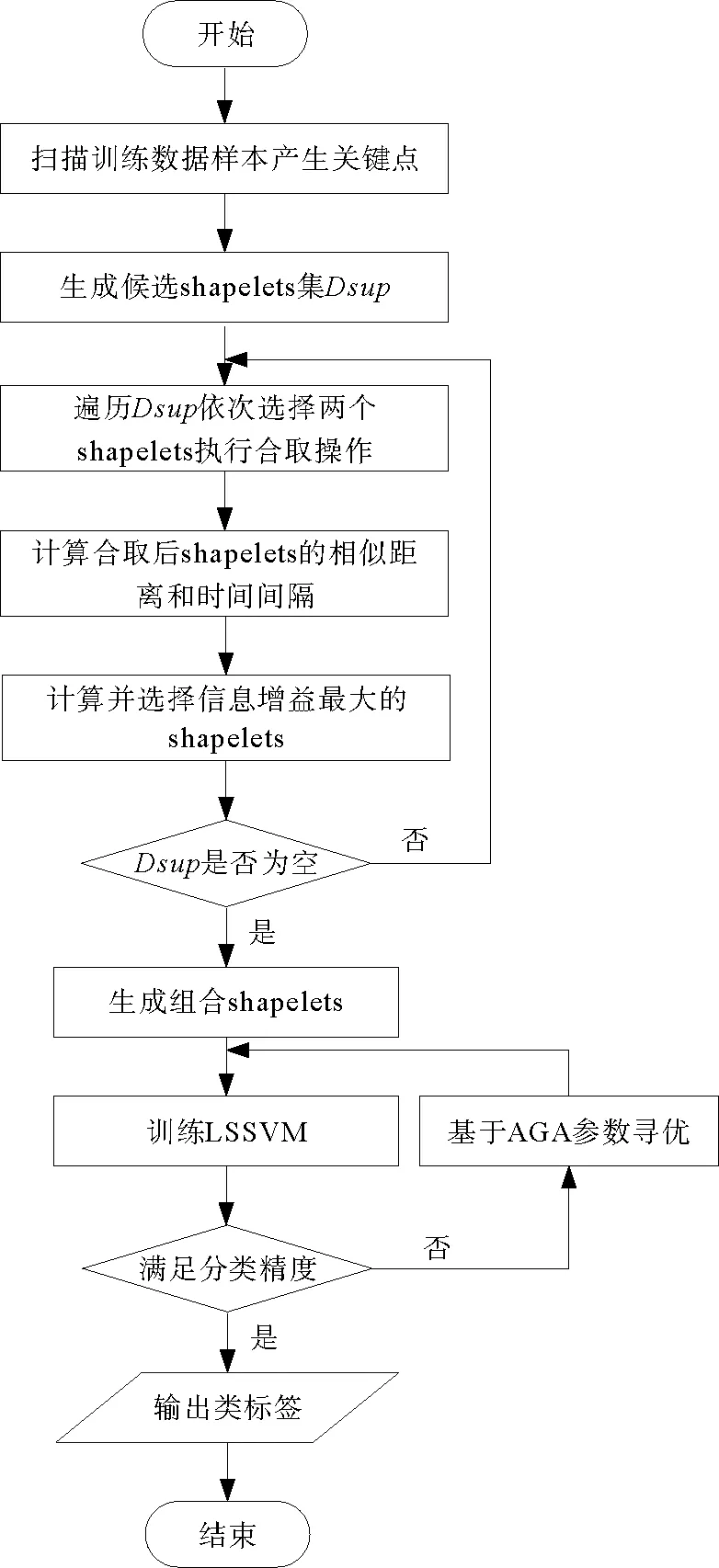
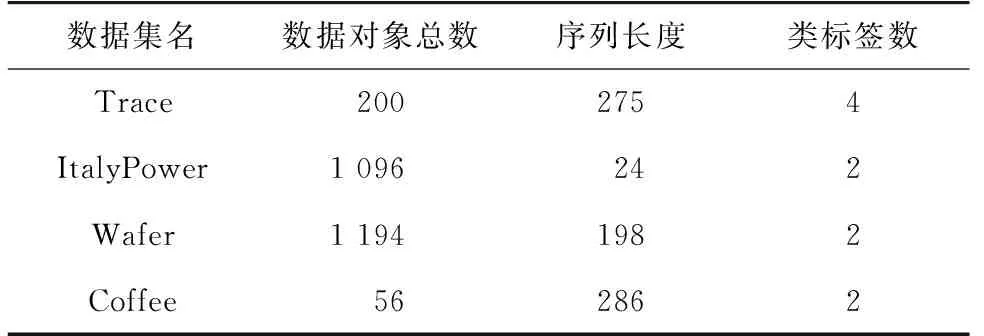
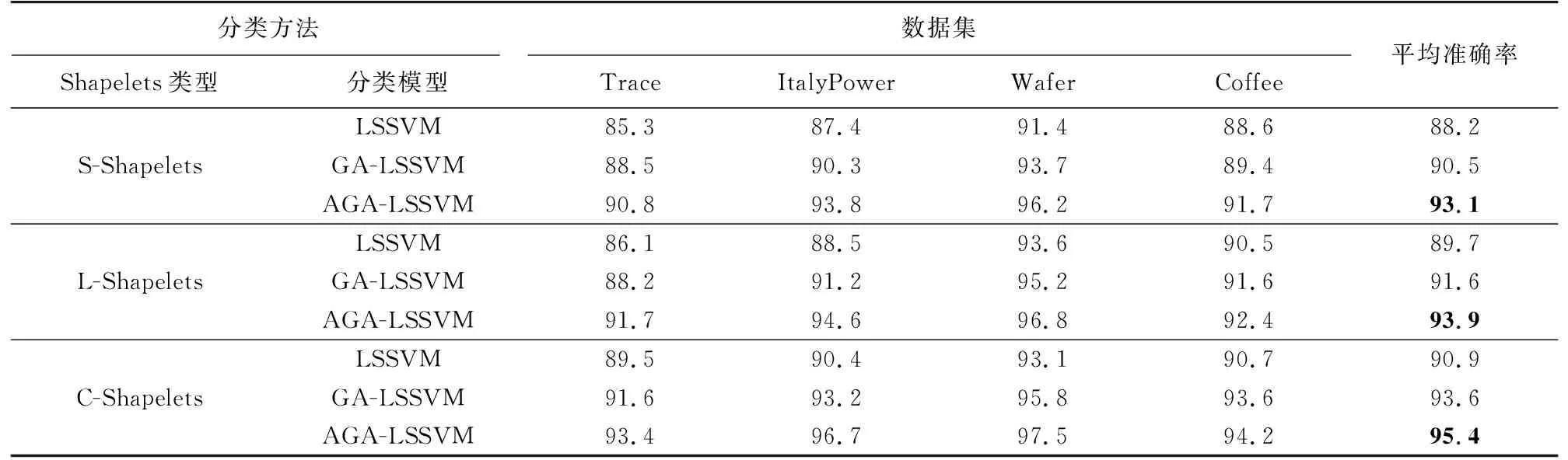
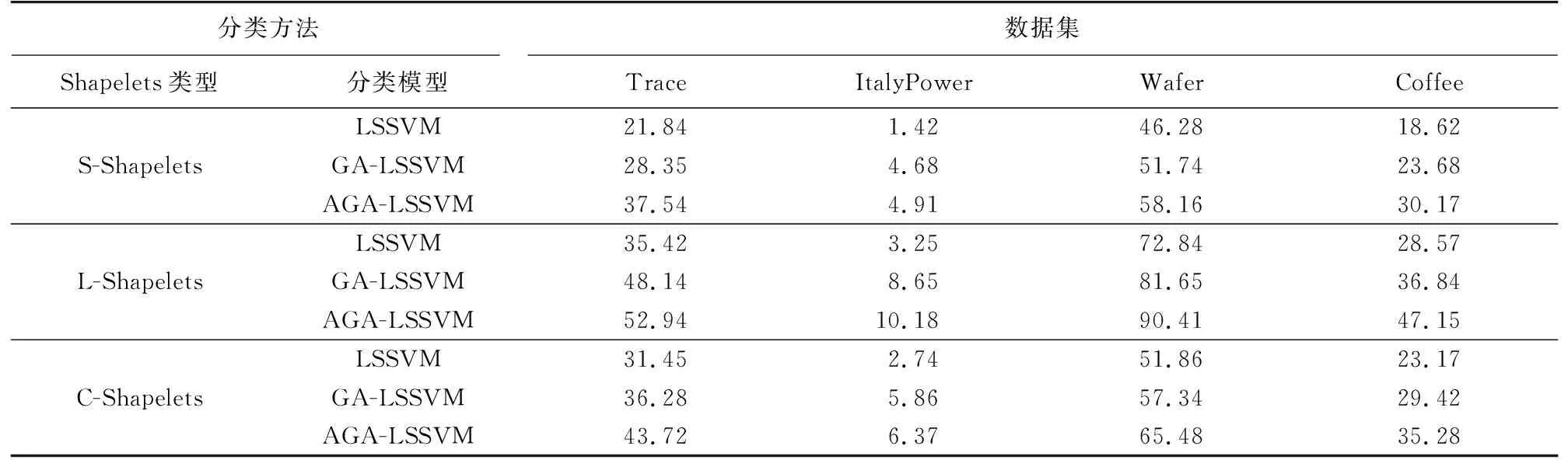
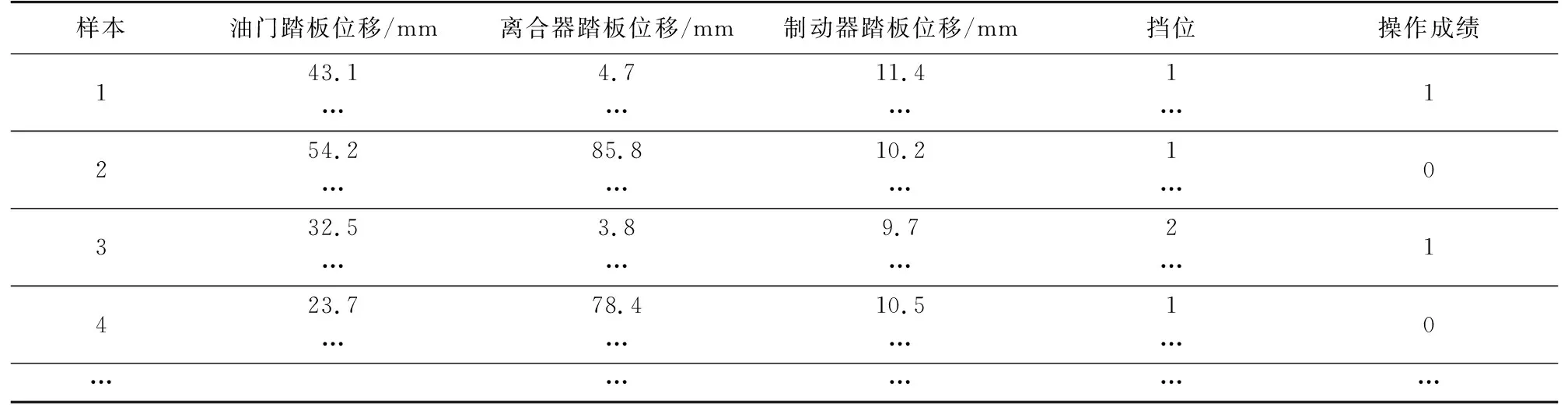
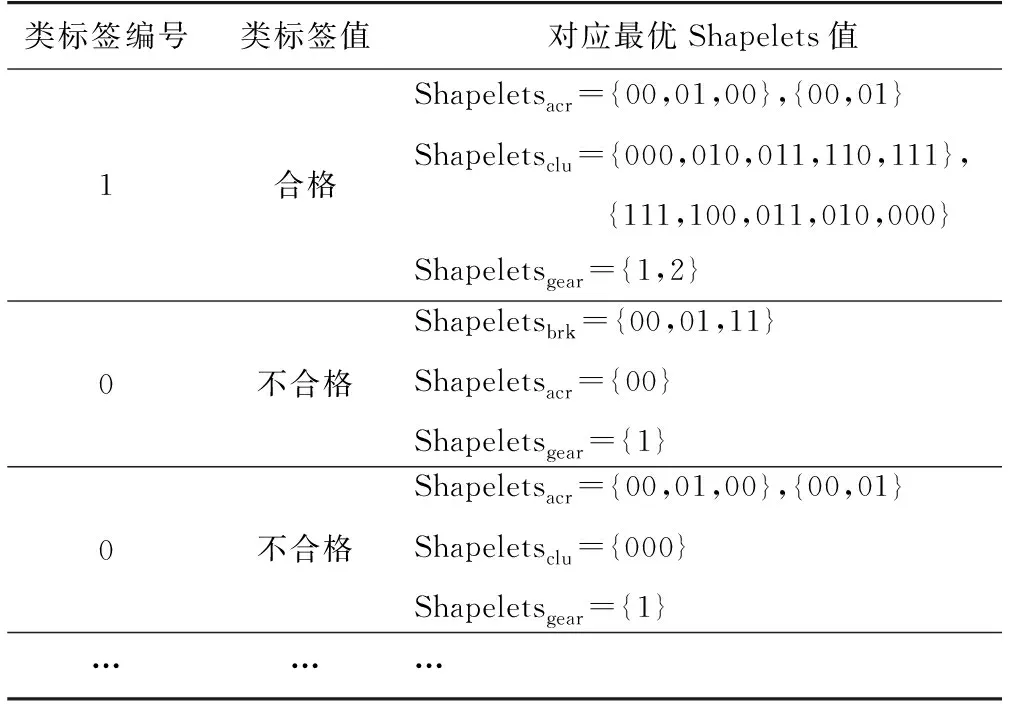
设Bpos(s1,TSi)、Bpos(s2,TSi)分别表示s1、s2与TSi的最佳匹配初始位置,并且Bpos(s1,TSi) Itime(s1∧s2)=Bpos(s2,TSi)-Bpos(s1,TSi) 。 (12) 对Canshp中的所有组合Shapelets按式(12)计算相应子序列的时间间隔,得到时间间隔集合 SItime={Itime(si∧sj)|Itime(si∧sj)=Bpos(sj,TS)-Bpos(si,TS),si,sj∈Canshp} 。 (13) (14) (15) 通过式(6)、(10)计算得到信息增益 (16) 选择信息增益最大的子序列作为组合Shapelets。 考虑到用LSSVM分类时,核参数σ和惩罚因子C的取值对分类算法的性能有重要影响,而且遗传算法具有良好的鲁棒性,故本节采用遗传算法进行参数寻优。但传统的遗传算法存在早熟收敛等问题,故采用自适应遗传算法改进交叉、变异操作,避免陷入局部最优。具体步骤如下。 1) 交叉操作 采用单点交叉算子,随机选择两个父代个体,并设置每一对个体的基因位置用于交叉操作。随着进化代数的增加,按式(17)自动调整交叉概率pc,然后在交叉点进行染色体互换,生成两个新的子个体。这种自适应变化克服了因采用固定交叉概率而导致的后期不易保留优秀个体的问题,有利于维护种群的多样性。 (17) 式中:τ为进化代数,psize为种群数量,len为染色体长度。 2) 变异操作 变异操作促使产生新个体,可以提高算法的局部搜索能力,变异概率设定过高容易破坏适应度最优的个体,导致收敛变慢;过低不利于产生新个体,容易陷入早熟。根据个体的适应度变化动态调整变异概率pm,对于适应度较小的个体赋予较大的变异概率,促进个体向更优解进化,反之赋予较小概率,即: (18) 式中:fitmax为种群中的最大适应度值,fitmin为种群中的最小适应度值,fiti为种群中个体i的适应度值,λ为调整系数,pm0为初始概率常数。 在获得组合Shapelets的基础上,利用Shapelets转换概念[16-17]计算原始时间序列与Shapelets之间的距离,将原始序列映射到新的特征空间,通过AGA-LSSVM算法进行分类。 假设xk∈Rn为经转换后的输入,yk∈R为类标签,则LSSVM将分类转化为如下优化问题: (19) 式中:ω为权重矩阵,b为偏倚变量,ek为训练误差,C为惩罚因子。 对式(19)的优化问题采用拉格朗日泛函得到下式: (20) (21) 结合卡库塔条件(Karush-Kuhn-Tucker,KKT),将式(21)转换为矩阵形式所表示的线性方程组: (22) 令A=Ω+C-1I,最终求得α和b分别为: α=A-1(Y-bH), (23) (24) 根据α和b的值,对任意输入样本x的分类函数为: (25) 对于多维时间序列数据集DTS={TS1,TS2,…,TSi,…,TSm}的任一维TSi,其输入样本子集可采用AGA-LSSVM方法学习训练出分类器,根据符号函数sgn()计算输出类标签,为: (26) 通过以上对CSAGA-LSSVM分类挖掘算法四个阶段的描述,得到CSAGA-LSSVM算法具体流程如图1所示。 图1 CSAGA-LSSVM分类挖掘算法流程图Fig. 1 Flow chart of CSAGA-LSSVM classification mining algorithm 为了验证CSAGA-LSSVM分类挖掘算法性能,设计多维时间序列数据的分类实验,分析该算法的分类精度和执行效率。 实验用计算机配置:处理器Intel(R) Core(TM) i7-4510@2.60 GHz,硬盘1 TB+128 GB SSD,显卡NVIDIA GetForce 840 M,内存8 GB DDR3,操作系统Windows 7 64位,编程环境为Python 3.7。选择公开数据集Trace、ItalyPower、Wafer和Coffee进行对比实验,数据集的简要说明如表1所示。 表1 实验数据集Tab. 1 Experiment data set 实验中分别利用基于采样Shapelets[18](S-Shapelets)、逻辑Shapelets[19](L-Shapelets)和本研究的组合Shapelets(C-Shapelets)对原始数据进行特征提取,其中S-Shapelets通过划分子类得到中心序列,选择与中心序列距离之和最小的序列作为采样数据,从而减少候选Shapelets的产生;L-Shapelets采用加速技术与剪枝方法过滤具有相似形状的Shapelets,从而增加更多有辨别能力的Shapelets用于数据转换,大大提高了分类的准确度。分别采用LSSVM、GA-LSSVM和AGA-LSSVM建立分类模型,共形成9种不同的分类方法。选取分类准确率和运行时间两个指标,对9种分类方法的性能进行实验测试对比。实验中采用8折交叉验证法将数据集划分为训练集和测试集,通过训练集对每个分类算法进行迭代训练,然后在测试集上进行检验,取平均值作为两个评价指标的最终结果。 1) 分类准确率 分类准确率是测试集上正确识别的样本数与数据对象总数的比值。9个分类方法在不同数据集上的准确率对比见表2。 表2 9个分类方法在不同数据集上的分类准确率对比Tab. 2 Comparison of classification accuracy of 9 classification methods on different data sets % 从表2可见,CSAGA-LSSVM分类方法的准确率要优于其他分类方法,且采用C-Shapelets的同一分类模型具有最高的准确率,说明C-Shapelets通过引入不同Shapelets之间的时间间隔对子序列进行组合,并根据信息增益选择最优的子序列,可以有效增强Shapelets的辨识能力,提高分类精度。同时基于C-Shapelets的AGA-LSSVM通过自适应遗传操作,比LSSVM、GA-LSSVM能搜索到更优的超参数解,对原始时间序列数据有更完整的特征表示,表现出更好的分类能力。另外,利用S-Shapelets的LSSVM在Trace数据集上的分类准确率较低,说明直接采用单个Shapelets对较长的时间序列进行分类,容易忽略不同子序列之间的关联,导致分类效果下降。而L-Shapelets采用剪枝策略对相似的Shapelets进行过滤,增加其他特征的Shapelets,具有较高的分类精度。 2) 运行时间 通过调用Python中time模块的时钟函数返回当前时间,用来计算算法运行的时间。表3为9个分类方法在不同数据集上的运行时间对比。 表3 9个分类方法在不同数据集上的运行时间对比Tab. 3 Comparison of running time of 9 classification methods on different data sets s 从表3可知,直接采用S-Shapelets的LSSVM分类方法所需时间最少,原因在于S-Shapelets没有进行不同Shapelets之间的组合运算,而是通过子类划分产生候选Shapelets,计算过程比L-Shapelets、C-Shapelets简单,并且LSSVM不进行参数寻优,因此整个算法的运行时间最少。基于C-Shapelets的时间序列表示充分利用具有显著特征的关键点,能够快速产生候选Shapelets,减少了相应子序列的搜索时间,从而算法的运行效率高。L-Shapelets在所有可能的子序列空间搜索候选Shapelets,空间复杂度较大,在产生Shapelets后还要进行迭代剪枝操作,故大多数情况下基于L-Shapelets的AGA-LSSVM所花费时间较多。另外AGA-LSSVM和GA-LSSVM采用遗传操作对LSSVM超参进行寻优,需要反复迭代直至全局收敛或达到规定的代数,因此运行时间相比传统的LSSVM要长,但准确率有所提高。 综上,CSAGA-LSSVM分类方法在准确率方面具有明显优势,适用于不同规模和密度的数据集,说明所提出的组合Shapelets能对原始时间序列进行更完整的特征表示。在运行时间上,基于C-Shapelets的AGA-LSSVM分类方法比S-Shapelets的LSSVM长,但比采用L-Shapelets的GA-LSSVM、AGA-LSSVM运行时间要少。综合考虑分类准确率的影响及分类模型训练的时间要求,CSAGA-LSSVM分类方法是可行的。 通过安装在某型坦克驾驶模拟器上的位移传感器、光电传感器实时记录受训人员的操作数据,模拟器系统帧频为25 fps,每运行1帧采集数据1次,即每秒采集25组数据。采集的操作数据主要包括起动开关、变速装置挡位、加油踏板、离合器踏板等。 为便于分析,对坦克驾驶操作分为基本操作和组合操作。基本操作是指驾驶过程只有一个操纵部件的状态发生变化,是驾驶操作的“元动作”。组合操作是由若干个基本操作按不同的顺序组成的动作序列,与动作次序、完备程度、完成时间等密切相关。换挡操作是适应不同路面环境下的机动要求,是坦克驾驶操作的一项重要内容。下面以“一挡换二挡”为例,运用CSAGA-LSSVM算法进行模拟训练结果分析。 在坦克驾驶模拟训练实验中,选择1 200名受训人员(二级坦克驾驶员、三级坦克驾驶员、初级坦克驾驶员和无等级人员各300名)在某型坦克驾驶模拟教室进行“一挡换二挡”操作训练,每名受训人员进行6次换挡操作,通过传感器和模拟训练系统采集到的驾驶员部分操作过程数据如表4所示。 表4 坦克驾驶模拟器“一挡换二挡”操作数据Tab. 4 Data of the tank driving simulator in “shifting from the first to the second gear” operation 从表4可以看出,油门踏板位移、离合器踏板位移和制动器踏板位移属于一元时间序列数据,变量取值随时间连续变化形成多变量时间序列。本次实验共产生7 200个样本,选择油门踏板位移、离合器踏板位移、制动器踏板位移、挡位值为特征变量,对操作成绩离散化处理为类标签y,形成决策表,如表5所示。 表5 坦克驾驶模拟器操作数据分析决策表Tab. 5 Data analysis decision of the tank driving simulator operations 从表5中随机选取80%的数据作为训练集进行分类器训练,余下的20%作为测试集。首先通过Shapelets特征提取方法对换挡操作的多维时间序列进行表示,求解组合Shapelets,再依次计算油门踏板位移、离合器踏板位移等时序数据与组合Shapelets之间的距离,实现换挡操作数据变换,用于后续分类输入;然后运用AGA求得最优超参数C=65.8,σ=0.25。基于调优后的分类模型对时序数据进行分类,最终得出分类结果如表6所示。 表6 结果数据Tab. 6 Statistics of Results 以表6为依据,结合坦克驾驶换挡操作的理论与实践,对得到的最终解分析如下: 1) “一挡换二挡”操作成绩合格所对应的Shapelets:油门踏板时序数据Shapeletsacr[1]∧Shapeletsacr[2]={00,01,00}∧{00,01},离合器踏板位移时序数据Shapeletsclu[1]∧Shapeletsclu[2]={000,010,011,110,111}∧{111,100,011,010,000},挡位时序数据Shapeletsgear={1,2},表示换挡前应平稳踩下油门踏板至适当位置,然后松开油门踏板同时将离合器踏板由初始位置踩到最大位置,迅速将变速杆由1挡推向2挡位置,挂挡后松回离合器踏板应做到前快后稳,同时均匀踩下油门踏板。 2) “一挡换二挡”操作成绩不合格所对应的Shapelets:制动器踏板位移时序数据Shapeletsbrk={00,01,11},油门踏板时序数据Shapeletsacr={00},挡位时序数据Shapeletsgear={1},表示“一挡换二挡”过程中踩下了制动器踏板,而未踩油门踏板进行冲车,车辆挡位值没有发生变化;油门踏板时序数据Shapeletsacr[1]∧Shapeletsacr[2]={00,01,00}∧{00,01},离合器踏板位移时序数据Shapeletsclu={000},挡位时序数据Shapeletsgear={1},表示“一挡换二挡”过程中未踩下离合器踏板,换挡操作不合格。 将“一挡换二挡”操作成绩为合格所对应的Shapelets组合可建立相应的标准操作动作模式,作为“一挡换二挡”操作技能水平的评价等级,对受训人员的驾驶动作进行精确分析。比如,随机选取一名受训人员的训练样本数据进行预处理生成相应的Shapelets,其中离合器踏板位移时序数据Shapeletsclu[1]={000,011,100,110},挡位时序数据Shapeletsgear={1}。通过计算与标准操作动作模式之间的距离,可以发现该名受训人员在换挡过程中没有将离合器踏板踩到底,导致挡位状态仍为1挡,挂挡不成功,表明该受训人员掌握动作要领较差,需要在今后的训练中加强理论学习,熟记换挡的关键动作和操作流程,同时注重模拟器基本驾驶动作训练,反复体会换挡要领。 本研究为挖掘坦克驾驶模拟训练数据,提出一种CSAGA-LSSVM分类挖掘算法。先根据起始点、结束点、阶跃点、极值点快速获取候选Shapelets,减少产生的候选Shapelets数量;再通过选择距离和时间间隔对Shapelets进行组合操作,并计算信息增益评价最优组合,增强特征的辨识能力,提升分类的准确性;然后设计了自适应遗传算法,通过动态调整交叉和变异概率来加速搜索LSSVM超参数的全局最优解,减少分类挖掘时间;最后,利用CSAGA-LSSVM算法分析某型坦克驾驶模拟器换挡操作数据,提取不同训练水平人员的操作特征,从而更好地发现训练问题,促进个性化训练的开展。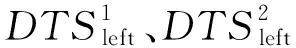
2.3 基于自适应遗传算法的LSSVM超参数寻优
2.4 基于组合Shapelets的AGA-LSSVM分类
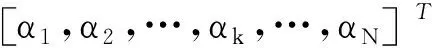

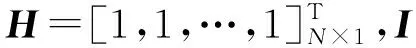
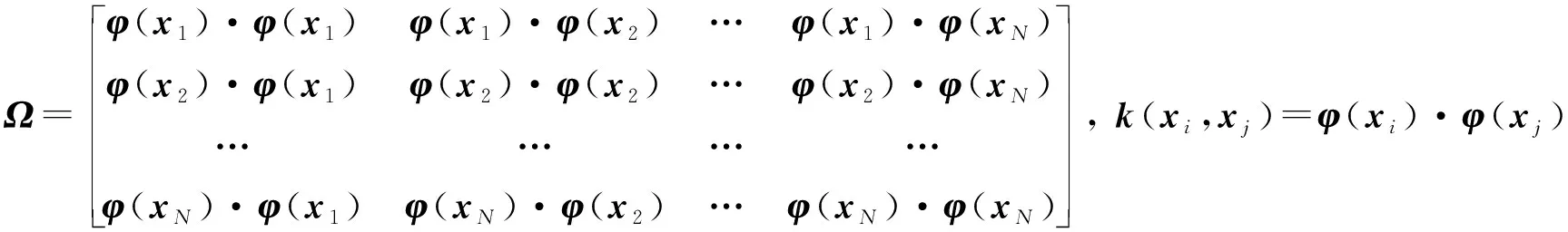
3 实验与对比分析
4 基于CSAGA-LSSVM的坦克驾驶模拟训练操作数据分析
4.1 数据来源

4.2 最优分类解获取
4.3 结果分析
5 结论

