改进D-S 证据理论在机床状态监测中的应用研究*

闫一佳 李建伟 闫献国 郭 宏

（1.太原科技大学计算机科学与技术学院 太原 030024）（2.太原科技大学机械工程学院 太原 030024）

1 引言

机床状态监测可以保证加工过程的稳定性和安全性，传统机床状态监测中单一传感器容易受到机床设备的复杂性和运行环境的不稳定性影响，会产生不确定性信息出现错误判断［1］。因此使用多传感器信息融合技术综合分析机床中多个传感器的信息数据，实现对机床的实时监控［2］是有必要的。其中D-S证据理论能够处理数据的不确定性，融和信息的能力优越，在信息融合、决策分析和人工智能等领域都有广泛应用，因此本文拟采用该理论实现机床监测中多传感器信息融合。

证据理论的研究主要分为两类：一是修改证据理论的经典组合规则，如YAGER［3］等方法，丁晗［4］的合成规则；二是不改变组合规则，在融合前对证据进行修正［5］，有MURPHY［6］方法，Xiao［7］的信息散度方法，赵秋月［8］的相似度计算方法和FANG［9］的基于灰色关联的修正算法。LIN［10］提出了一种包含证据理论和多粒度粗糙集理论的两级融合方法，田明明［11］使用了迭代算法修正冲突证据，FRIKHA［12］提出了一种综合了多个准则的改进层次分析法，可以消除主观性和减少不一致性。SARABI［13］提出了一种适用于文本估计的多标准可信度聚合折扣方法，用于解决从多个证据来源引发的冲突，但文献只针对证据本身来计算可信度和冲突。

近年来，证据理论的研究受到了越来越多研究者们的关注，更多关于证据权值的生成方法也随之被提出。但大多数都是对证据本身进行修正而忽略了传感器数据本身的不确定信息。本文重点对证据源进行不同层次的信任度分析，基于分批估计思想，提出了一种新的进行二次可信度修正的D-S证据理论优化方法。本方法首先引入分批估计理论计算传感器可信度以减少采集数据过程中的干扰，建立一种基于传感器可信度的修正方法；接着根据基本概率分配函数（basic probabil-ity assignment function，BPA）构建证据偏离度，对获得的证据进行二次修正；最后对经过二次修正的基本概率分配函数进行融合，完成决策和信息处理过程。

2 D-S证据理论基本原理

D-S 证据理论由20 世纪60 年代的哈佛大学数学家A.P.Dempster 提出，他的学生G.shafer 做了进一步发展。证据理论首先要确定一个包含互不相容的基本命题组成的识别框架，表示某一问题的所有可能答案。基本概率分配函数是在识别框架上对应的mass 函数，反映着证据体对某一命题A 的信度大小。并且满足：

其中Φ为空集，K为冲突系数，反映了证据之间的冲突大小，公式如下：

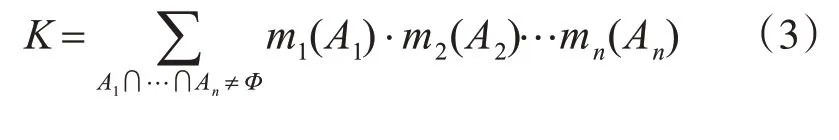
3 二次可信度修正的证据理论优化方法

由于传统机床状态监测中传感器容易受到机床设备的复杂性和运行环境的不稳定性影响，获取的信息可能是不精确的。为解决上述问题，从传感器本身误差和证据体冲突两方面出发，提出一种二次可信度修正的证据理论优化方法。融合算法流程如图1所示。

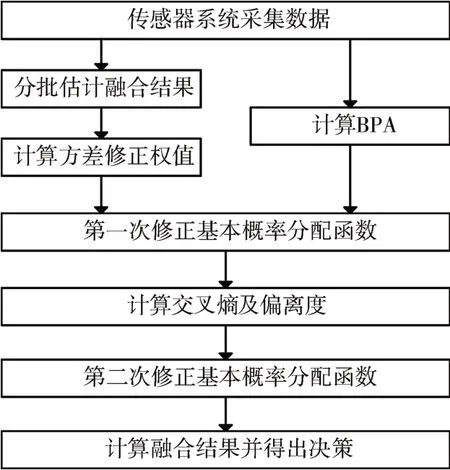
图1 算法流程图

算法首先根据分批估计算法对源数据进行融合，融合结果用来获取其与节点数据的相对方差，以得到传感器可信度，同时对根据源数据获得BPA进行第一次修正。之后计算证据体之间的偏离度来表示其冲突，进行第二次修正。最后使用融合规则得出决策结果。

3.1 传感器可信度数学模型

传统机床状态监测中传感器测量的数据会受影响出现误差，当误差数据参与证据的生成时，很有可能会产生冲突证据，因此需要依据误差数据产生的不确定性评估传感器可信度［14］。本文从证据源的不确定性出发，分析传感器可信度对BPA进行第一次修正，减少证据不确定性。

传感器所收集数据的误差会导致所测数据序列方差的波动，数据波动越大，数据误差越大。因此引入分批估计理论思想来获取节点可信度。

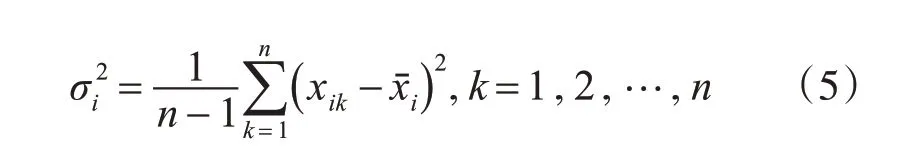
根据方差对节点在周期内的测量值进行融合，应用分批估计理论得到初步融合结果如下：

代入后可得融合权值ωi及融合结果x'：

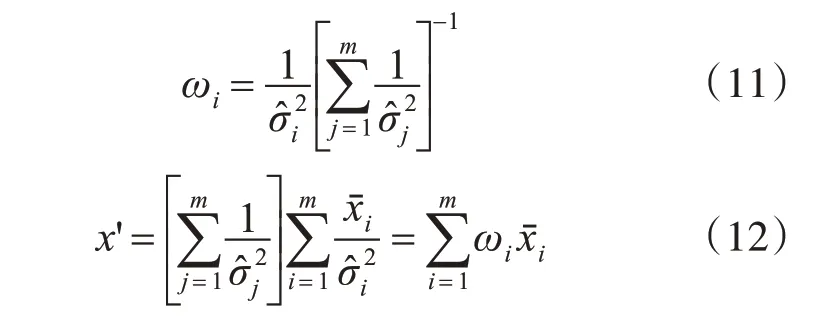
再由得到的分批估计融合结果x'来计算其与节点数据xij的相对方差，相对方差可以表示当前传感器数据序列与估计值的差异程度，再根据相对方差计算每个传感器的质量。相对方差［15］计算如下：

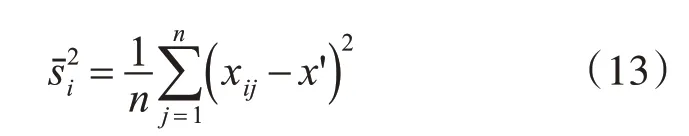
然后计算每组数据的调整因子αi来对融合权值ωi进行调整，调整后的权值作为传感器可信度。传感器可信度应与估计方差成反比，并且各权值相加和始终为1，因此，αi计算如下：

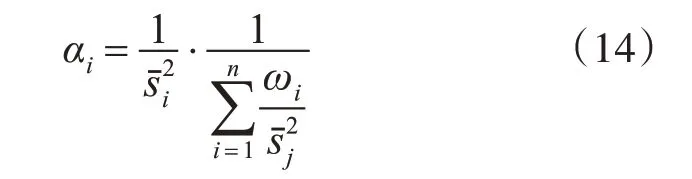
将调整后的权值计算如下：

计算得到每个节点可信度后，以每个节点在一个周期内的均值作为该周期的采集数值来计算该时段节点的基本概率分配函数。获得基本概率分配函数后，再依据节点可信度对其进行第一次修正。

3.2 BPA获取数学模型

证据理论基础是BPA 的获取，一个好的BPA应该包含数据源提供的大部分信息，有清晰明确的对应特征值，并且适用于后续融合过程。隶属度函数是常用的基本概率分配函数计算方法之一［11］，通过选取适当的隶属度函数，可以在状态监测中的过程中最大化保留不确定性的概率［16］。

根据机床检测传感器输出和专家知识，选择高斯隶属度函数作为状态监测的基本概率分配函数。高斯隶属度函数如下，其中xˉi为该状态对应的特征值：

则根据3.1 节中计算得到的传感器修正权值，且第i个证据对不确定的故障种类的修正概率分配函数为mi(Aj)，则基本概率分配函数计算如下：

3.3 基于偏离度的冲突模型

数据的不确定性可能会造成冲突，因此需要度量证据不确定性［17］，以此第二次修正基本概率分配函数。一般来说常采用证据间的相关性或者距离［18］来衡量证据间的冲突程度，本文为了充分利用冲突信息，提出了一种交叉熵的测度方法。交叉熵可以充分表达两个不确定性信息之间的差异性。

由于模糊交叉熵不具有对称性，因此m1和m2之间差异性距离可计算为

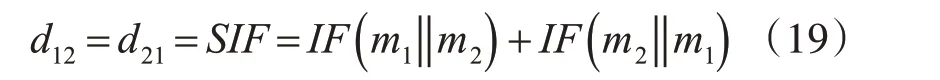
则差异性矩阵定义如下：

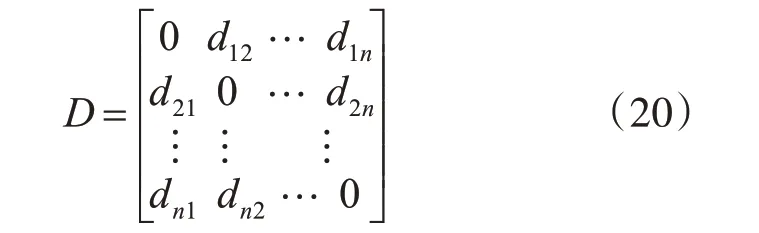
根据差异性计算证据相异度，如果一个证据和其他证据的差异性大，表示证据的支持度较低。则第i个证据与其他证据的相异程度可计算为

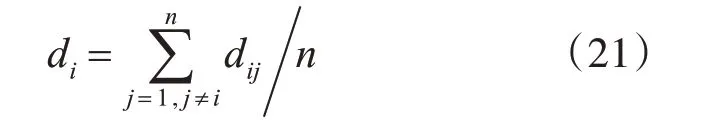
则定义一种自适应偏离度为

依据偏离度对证据的基本概率分配函数进行修正，计算证据权重如下：

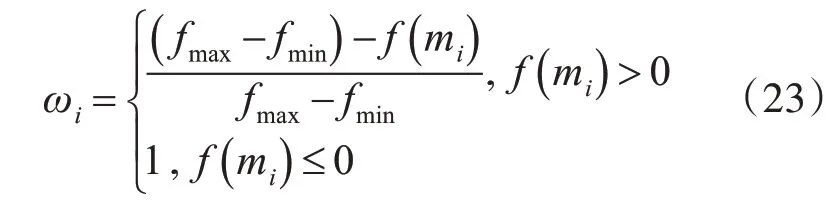
这样就确定了各证据的权重系数，把权重作为第二次修正折扣因子对证据进行修正，减少冲突证据在组合规则中作用的同时充分利用原始证据信息。公式如下：

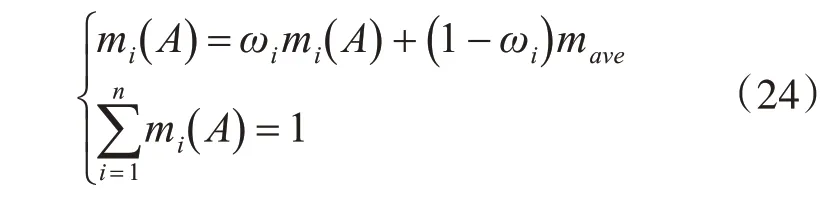
进一步归一化，可以完成对BPA 的重新分配，再使用证据理论合成公式进行合成。合成后使用如下规则进行决策，满足下述公式时，为决策结果：

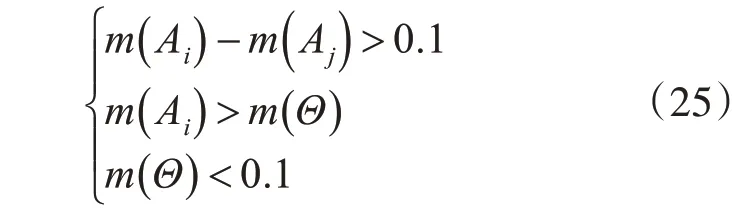
基于上述步骤可以完成对机床监测过程中多传感器采集的数据处理融合，该方法从数据源和证据体两方面出发，加入了传感器的可信度和证据体的差异性衡量，以此提高融合结果准确率和鲁棒性，减少机床监测中不确定性因素对状态决策的影响。

4 基于D-S 理论改进算法的机床工作状态监测诊断实例

4.1 二次修正证据理论的机床状态监测过程

基于上述理论，研究团队构建了机床状态监测的多传感器数据融合验证平台，来验证基于二次修正思想改进的D-S 证据理论相较于传统证据理论的优点，验证步骤设计如下。

1）构建机床状态辨识框架。使用机床状态监测中的多个传感器测量的先验数据进行特征提取，根据特征值、隶属度函数构建识别框架和BPA 函数。

2）采集机床状态数据信息，以周期计算各传感器的可信度及BPA。根据当前周期内的各个传感器数据，利用分批估计计算各个传感器的可靠性，并在获得BPA后依据可靠性对其进行第一次修正。

3）计算偏离度修正的BPA。根据交叉熵来计算各个证据体之间的差异度，再计算自适应偏离度对BPA进行第二次修正。

4）证据融合。根据融合规则对修正完成的BPA 进行组合，获得最终融合结果，再比较融合结果得出决策，获取机床工作状态。

4.2 诊断实例分析

传统机床状态监测中，温度信号反映了机床加工过程中的状态，影响加工精度的变化，是机床状态监测的一个重要指标。因此本文使用普通车床CA6140 在加工过程中的温度为研究对象，将获取的红外温度数据进行处理融合来获取决策结果。

如图2 所示，试验台安装红外热成像仪，试验数据采集系统设定0.008s 采集一次加工刀尖位置区域的温度值，以此获取机床加工工作状况的试验数据，设置主轴额定转速为320 r/min，切深0.5mm，进给量为0.1mm/r。

图2 试验台展示图

针对机床加工过程试验台正常工作状况的试验数据进行拟合研究，使用先验数据提取特征参数后，得到工作状态诊断的基本概率分配函数和识别框架Θ={A1，A2，A3} 。其中，A1为工作状态正常，A2为工作状态无法确定的情况，A3为加工状态出现异常，可能有故障发生。

如图3 所示，使用红外热像仪采集加工过程中刀尖位置四个区域内的温度数据，其中，设置区域1 偏离切削加工范围，所采集的数据相对正常数据存在较大偏差，作为异常数据样本使用（表1）。

图3 红外热像仪采集图像

红外热像仪中的每个区域作为一个证据体，将证据体E1、E2、E3、E4在同一个周期内的数据作为试验样本（表1）输入到已经搭建好的模糊隶属度函数进行初步计算，构造得到BPA集（表3）。

根据表1 的温度数据，首先计算每个传感器在一个周期内获得数据序列的平均值和第一次修正权值如表2 所示，从表2 中可以明显看出区域1 的数据修正权值过低，即认为该区域收集数据可信度小。

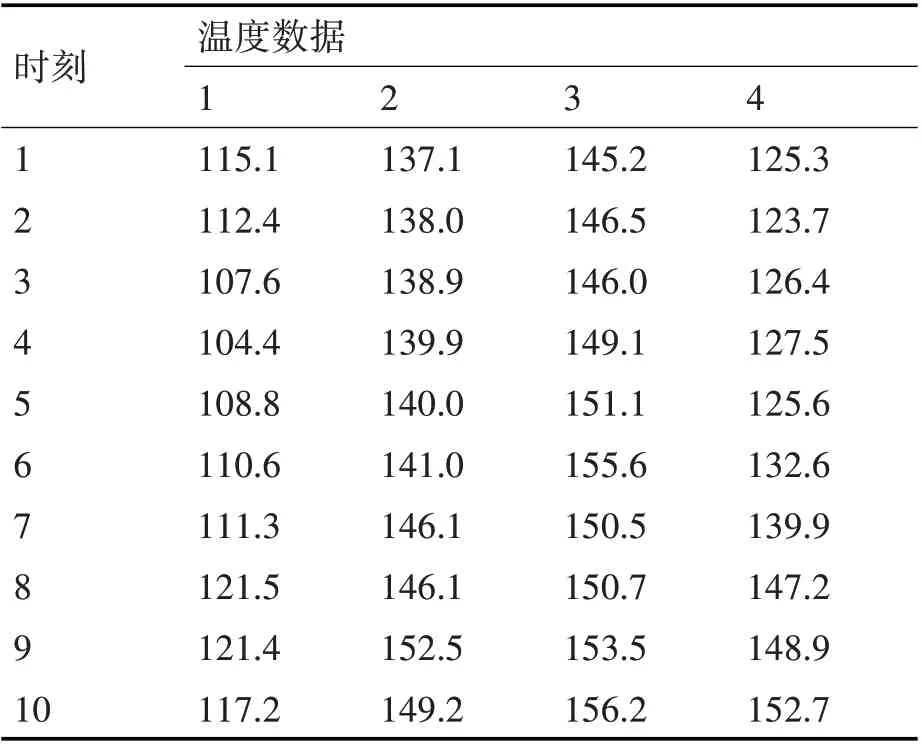
表1 各区域在一个周期内上传的数据

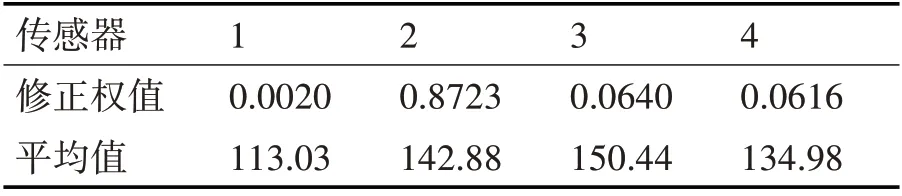
表2 各区域的修正权值及均值

平均值作为测量数据通过模糊隶属度函数计算得到各个传感器的隶属度，即BPA，见表3。

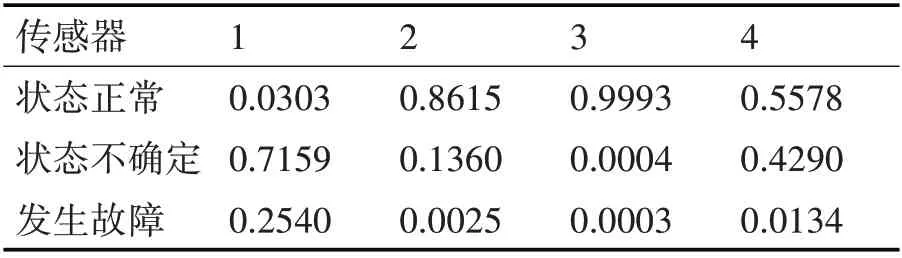
表3 各区域数据对应BPA

分析表3 可以发现，证据体1 的BPA 与其余证据体存在明显的冲突，不同的证据体对该周期机床的加工状态得到的诊断结果不同，根据单个证据体进行状态识别，可信度偏低，有时可能无法准确识别出工作状态，甚至对证据融合造成负面影响。

根据修正权值对BPA进行第一次修改如表4。

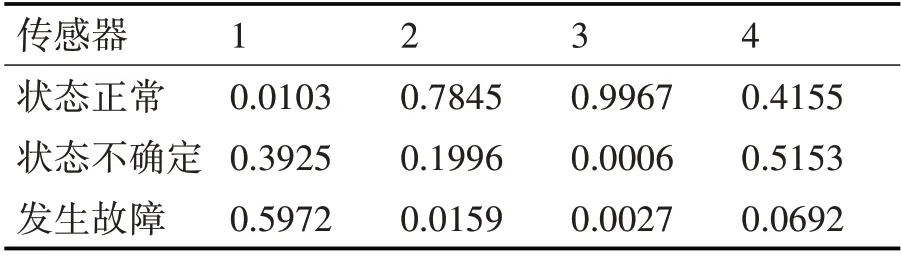
表4 第一次修正的BPA

根据偏离度对基本概率分配函数进行第二次修改，偏离度计算如下：

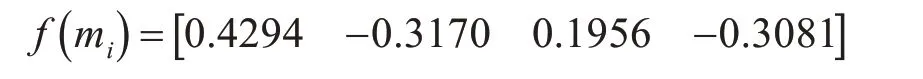
再依据偏离度计算权值，由式（24）可计算出，自适应阈值判断证据体2 和证据体4 偏离度小，与整体证据差异度较小，冲突度较低，不需要进行修改，则根据权值对证据体的BPA 第二次修正如表5。

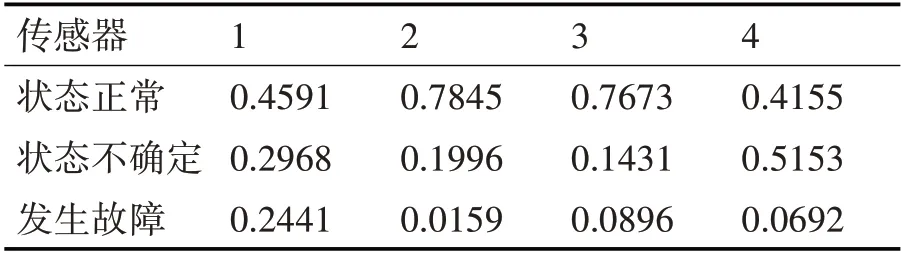
表5 第二次修正BPA

分析表3 和表5 可以发现，经过二次修正后的BPA 稳定性增强，异常证据体1 中A1的置信度由0.0303 提高到0.4591，由此说明，经过二次修正可以有效提高冲突证据体对正确状态的概率分配，有利于提高后续融合结果的准确率。

分别使用本文的二次修正证据理论算法和原证据理论、孙全、叶青提出的算法进行融合，可得出结果为表6。依据得到的融合结果对机床状态进行决策得出当前状态为正常，与真实状态一致。

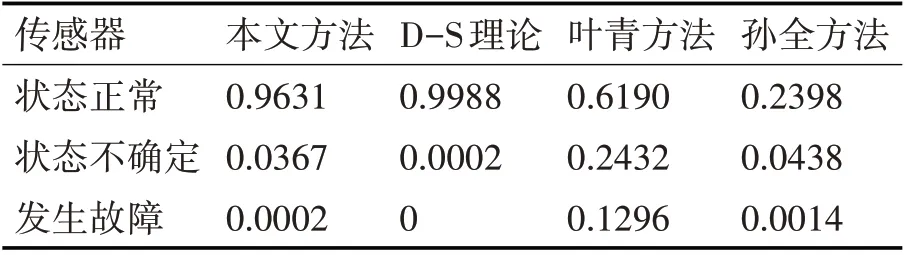
表6 融合结果及对比

分析表6 可以发现，当融合后A1的BPA 在本文方法中的值要高于叶青、孙全的两种经典算法，而证据理论A1的BPA高于本文方法是因为证据体2、3的数据存在0悖论情况。因此选取八组数据样本，用证据理论和本文算法处理，得出结果如表7所示。

分析表7，可看出本文算法鲁棒性高，能避免由于0 悖论得出的错误融合结果。说明本文算法应用在机床状态监测中可以有效地通过对多个证据体融合来减少状态识别的不确定性，同时融合后的可信度比融合前单一证据体独立判断情况下的可信度有明显提高，优于传统机床单一传感器的监测识别率，能够准确实现对加工过程状态的识别。

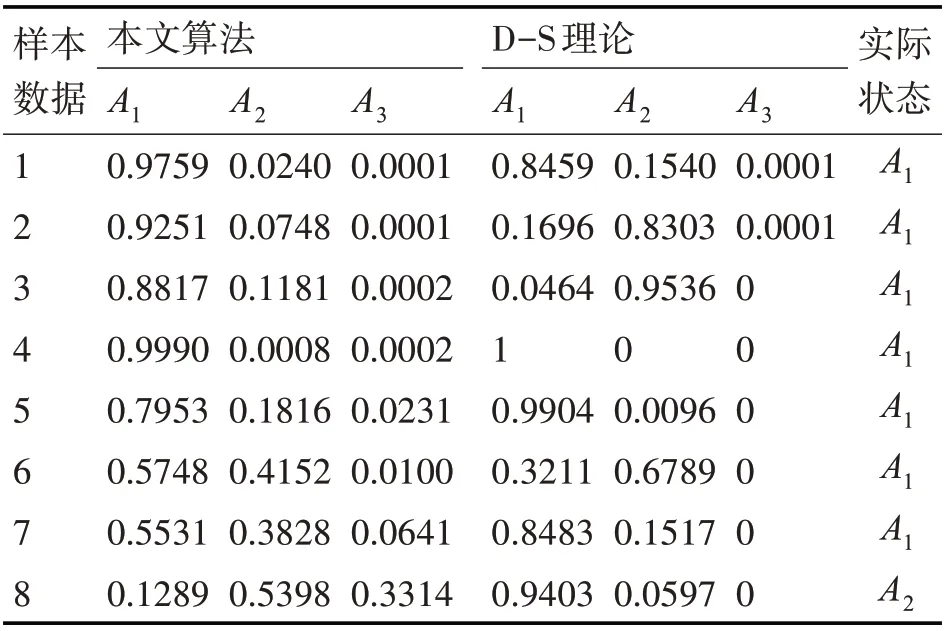
表7 两种方法融合结果及对比

5 结语

本文提出了一种基于二次修正的D-S 证据理论在机床工作状态监测中多传感器数据融合的方法。该方法使用高斯模糊隶属度函数来计算BPA，根据分批估计和交叉熵分别衡量传感器的可信度和证据体本身不确定性，对BPA 进行二次修正，融合各个证据修改后的BPA得出最终决策，从而实现对机床加工过程中工作状态的判别。通过融合结果可以看出，本研究提出的算法可以通过对BPA进行修正后解决证据冲突和0 悖论问题，且融合效果相对较好，能有效排除异常数据对结果的影响，准确识别机床的工作状态。这说明本算法可以提高工作状态识别的准确率和鲁棒性。