基于RRT 算法的障碍物移动模型研究*

汤小芳 杨余旺 郭利强 谢勇盛 赵启超 李 操

（南京理工大学计算机科学与工程学院 南京 210000）

1 引言

MANET 网络由若干自由移动的无线节点构成，节点之间的通信无需基础设备的支持，每个节点不仅是通讯终端，还能作为中继节点负责转发数据［1］，其组网方式灵活，网络拓扑变化频繁。目前，关于移动自组网的相关研究大多在仿真软件中进行，而如何根据特定的仿真场景来选取与之相匹配的移动模型成为研究的基础和关键，越是接近现实场景的移动模型才越具有研究和使用价值。基于现实需求，人们在现有的传统移动模型（例如RDM、RWPM、RWM 等）上进行了各种优化，但是，这些移动模型大多是采用简单的、随机的直线运动机制［2］，节点通过随机函数生成一个随机的目的位置或运动方向，以特定的速率前进到目的位置［3］。这些移动模型往往设计简单，更适用于空旷、无障碍的环境。然而，现实中各种障碍物（如树木、建筑物、人群等）随处可见，实物很难始终保持直线运动状态。所以，当存在障碍物时，这些传统的移动模型已经不再适用。

本文选取随机路点移动模型（Random Waypoint Model，RWPM）为研究对象，引入快速扩展随机树（RRT）算法，在起始点和终点之间快速寻找到一条能避开障碍物的有效路径。RRT 算法作为一种新颖的随机节点采样算法，具有建模快、搜索能力强、易于扩展等优点，将其应用在多障碍环境下的移动模型中，不仅能增强模型的现实性，还能使模型具有更优的概率分布。

2 经典节点移动模型

2.1 随机路点移动模型

随机路点移动模型，是由CMU（Carnegie-Mellon University，卡内基—梅隆大学）提出的，它运行机制简单，适用性强，已经成为研究MANET路由协议的标志性移动模型［4～5］。在NS2 中，RWPM 的实现过程大致如下：首先，每个节点nk在活动区域内随机生成一个目的位置Pi；然后，它在区间［Vmin，Vmax］中随机选取一个速度vi，接着，以速度vi向着Pi前进；到达Pi后，ni暂停一段时间Tpause，该过程称为一个step；Tpause结束以后，nk继续在活动区域内随机选取一个新的目的位置Pi+1和速度vi+1并向着Pi+1前进。整个过程周而复始，直到仿真时间结束［6］。

2.2 存在的问题

虽然RWPM 一直被大多数网络仿真软件采用，但是如果要仿真障碍物存在的场景时，RWPM却不是最优的选择。在现实场景中，障碍物的存在是一种十分普遍的现象，行进路线经常会受到障碍物的干扰［7～8］。在RWPM 模型中，节点在选定的起点和终点间沿直线前进，因此，若想在仿真中规避障碍物，必须保证起点和终点的连线不触碰任何障碍物，尤其当仿真区域内存在数量较多、规模较大的障碍物时，这会大大限制每一次终点的选择范围，这与现实场景相背离。

3 RRTMM模型

快速搜索随机树算法（Rapidly-exploring Random Tree，RRT）是一种增量式随机采样算法，其优点是无需对搜索区域做几何划分和空间建模，就能有效解决有代数约束和微分约束的复杂空间路径规划问题［9～10］。该算法搜索空间覆盖率高，搜索范围广，尽可能地探索未知区域，能够在复杂的多维空间有效规划出一条合理路径。

RRT算法将某一初始点作为根节点，在每一轮的生长中，根据随机生成的采样点来逐步扩展叶子节点，从而生成一个随机扩展树，直到树中的某个叶子节点触及目标点或抵达目标区域，就认为搜索到了一条由起点到终点的有效路径［11～12］。RRT 算法的描述如图1所示。

图1 RRT算法描述

在随机树的生成过程中（1～10 行），假设初始点为qinit，目标点为qgoal，最初的随机树仅由qinit这一个根节点构成；在规定的循环次数范围内，首先，SetTarget 函数的作用是在空间内随机产生一个采样点qtarget（3行）；然后，Nearest函数找到该随机树上与qtarget距离最近的节点qnearest（4 行）；最后，由Extend函数在qnearest节点上沿qtarget方向生成一个新的叶子节点qnew。若qnew触碰到障碍物，则返回NULL，表示本轮叶子节点扩展失败，进行下一轮扩展；否则，qnew被添加到随机树中（7～9 行）。循环执行上述步骤，当qnearest和qgoal的距离小于某个阈值，则表示寻找到了一条从初始点为qinit到目标点为qgoal的有效路径，搜索成功（5～6行）。

4 RRTMM评估

在MANET的仿真实验中，移动节点（MN）的轨迹通常取决于节点的动态特性，往往表现为在仿真期间节点轨迹覆盖仿真区域Ω的情况，即Ω内的节点概率分布。本文假设所有的MNs 在二维仿真区域Ω内独立运动，互不干扰，所有的MNs 都具有相同的移动属性。因此，可以通过研究某一个MN nj在不同场景下的概率分布，因为它的渐近空间分布与其他的MNs相同［13～15］。

如图2 所示，假设将Ω平均分成50 × 50 份，用grid（s，t）表示Ω内的任一网格，其中（s，t）∈（1，2，…，50）。假设每个grid（s，t）都装有计数器，只要当MN经过该处时，其计数器自动加1。用Ni（s，t，k）表示nk当前已经过grid（s，t）的次数，nk从当前位置Pi（x，y）移动到下一个位置Pi+1（x′，y′）所穿过grid（s，t）的次数用Ni+1（s，t，k）来表示。若nk在移动的过程中经过了grid（s，t），则有

图2 节点nk穿过网格grid（s，t）的情形

如果用α（s，t）来表示节点nk在网格grid（s，t）上的概率，则有

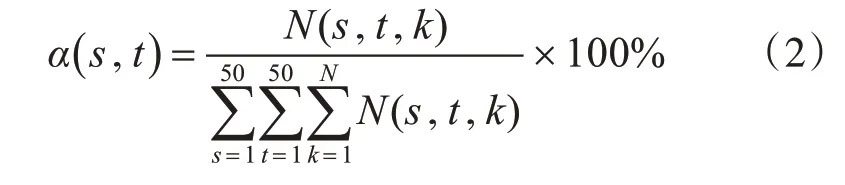
利用上式，可以很方便地计算出所有节点位置在Ω内的不同子区域上的概率分布。

5 仿真实验结果及分析

5.1 仿真环境设置

为了验证RRTMM 模型，分别在RWPM 和RRTMM 的仿真区域Ω内设置两组相同的障碍物｛Oi|i=1，2，…，n｝，当MN随机选定的目的位置Pi+1与当前位置Pi的几何连线穿过Ω内的障碍物Oi时，RWPM放弃当前选定的目的位置，重新选择新的目的位置Pi+1，直到Pi和Pi+1的几何连线与Oi无交点。与RWPM 的不同之处在于，当MN 运动到目的位置Pi+1会触碰到障碍物时，RRTMM会利用RRT算法在目的位置Pi+1和当前位置Pi之间快速寻找到一条绕过障碍物Oi的可行路径，当起、终点连线未触碰到障碍物，则直线前进。本实验利用Matlab 仿真工具，并设计两种不同的障碍物场景来进行仿真实验。本实验所涉及的仿真参数如表1所示。

表1 仿真参数

在场景1 中，设置一个半径为10m 的圆形障碍物，圆心位于仿真区域Ω内的中心。在场景2中，设置五个同等大小的的圆形障碍物，每个障碍物的半径也均为10m。

5.2 仿真结果及其分析

为了验证RRTMM 模型，仿真过程和评估方法如下：首先在除障碍物之外的Ω内指定任意起始位置Pi和目的位置Pi+1，当Pi和Pi+1之间的几何连线穿过障碍物Oi时，RRTMM 根据RRT 算法寻找到一条最近的可行路径；在MN 运动的过程中，每当MN 的轨迹经过一个网格grid（s，t）时，该网格的计数器自动加1，经过1×104个step 后，得到所有网格的计数器值；最后画出该MN在Ω内的节点概率分布图像。

图3、4 和图5、6 分别为RRTMM 模型和RWPM模型在两种不同障碍物场景下的节点概率分布图像。

图3 RRTMM模型在场景1中的节点概率分布图

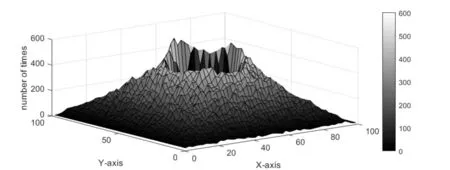
图4 RWPM模型在场景1中的节点概率分布图

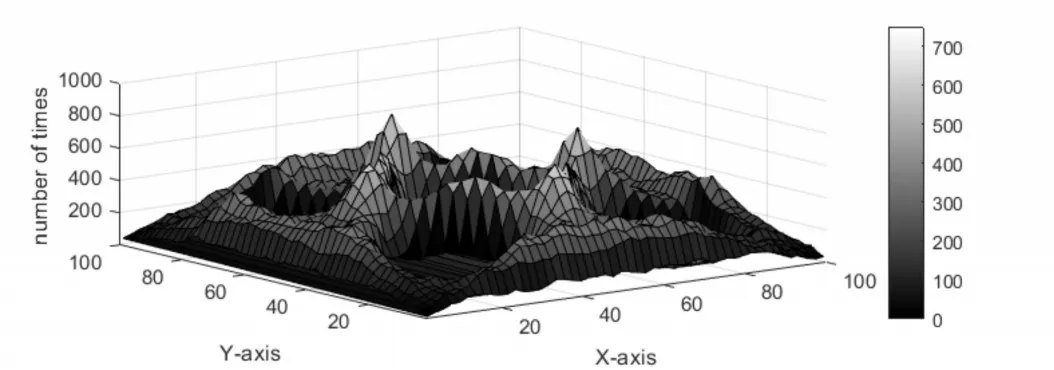
图5 RRTMM模型在场景2中的节点概率分布图

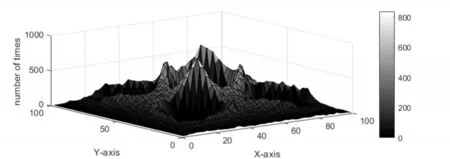
图6 RWPM模型在场景2中的节点概率分布图

如图3 和图4 所示，在场景1 中，这两种MM 在概率分布上有一定的相似之处：在障碍物区Oi中，即图像中间凹陷下去的部分，MN 出现的概率均为0，并且整体概率分布呈现中心密集四周稀疏的状态，这符合已有研究发现的泊松分布。而不同之处在于：RWPM 的节点概率分布在中心区域更加密集，而RRTMM 在障碍物周围的区域分布明显更加均匀，曲线过渡也较为平滑。这是因为，RWPM 模型虽然设计简单，但其节点的非均匀分布会随着仿真时间的延长而更加严重；RRTMM 模型在节点运动需要绕过障碍物的情况下，调用RRT 算法来搜寻一条最短的可行路径，RRT算法本身具有很强的随机性，这有助于缓解MN 向中心聚拢的趋势，所以MN分布更加均匀。

从图5、6 可以看出，当Ω内的障碍物数量增加时，五个障碍区内的概率均为0；从整体看来，RRTMM 仍然体现出较优的概率分布，这体现在障碍物周围区域的分布比RWPM 更加均匀，曲线过渡也更加平稳。这说明RRTMM 模型能够适应多障碍物场景。

6 结语

本文针对多障碍物场景，首次提出了一种基于RRT算法的移动模型，该模型能在复杂的障碍物场景中快速搜索到一条可行路径。通过仿真对比实验，在同等障碍物约束的条件下，该MM 比传统的RWPM具有更优的节点概率分布，障碍物周围区域的分布更加均匀，曲线过渡更加平滑。本MM 更加真实地模拟了现实场景中节点的运动情况，这为后续相关路由协议的仿真提供了可靠的基础。