深度算法预测模型的数据优化*

程劲松

（南京航空航天大学 南京 211106）

1 引言

长久以来，对于某一类需要深入研究的计算问题，比如经典的决策问题中的P 与NP 问题，人们总是尝试开发更高效的求解算法。随着研究的不断深入，这些领域或多或少已经积累了大量各式各样的求解算法。然而，在面对不同的问题实例时，没有哪一种算法可以始终优于其他算法。这种现象被称为算法性能互补，即不同的算法在不同的问题实例上都能取得最佳的性能表现。绝大多数的NP决策问题或优化问题上都有算法性能互补［1～4］的身影，其中就包括布尔逻辑可满足性问（Boolean Satisfiability Problem，SAT），约束满足问题和旅行商问题等，以及近些年来热门的机器学习领域。这些类型的问题目前不存在一套完整的可以指导如何选取求解算法的理论，即使存在，它也仅存在于少数特殊的问题类别中，并不能适用于更为普遍的情况。

在这种环境下，算法预测（Algorithm Selection）［5～6］问题逐渐受到人们的重视。给定一个计算问题、一组可能解决该问题的算法以及一个待解决的特定的问题实例，如何确定哪些算法可以在该问题实例上取得足够优秀甚至最佳的性能是算法预测的目标。自从Rice［5］首次系统地提出这个问题，单实例算法预测问题以及相关的算法就一直吸引着人们的目光，现如今已开发出众多优秀的算法预测系统，例如SATzilla［7～8］，CSHC［9］和ALORS［10］等。后来，Loreggia［11］将深度学习［12］应用在算法预测任务上，首次实现了数据集特征的自动提取。尽管如此，目前关于深度学习在算法预测问题上的应用依然存在着很多的局限性。该方法最大的问题就是深度学习根深蒂固的老问题，即数据集的数量与质量对于训练强大的深度模型至关重要。因此，本文就从数据优化层面评估深度模型在算法预测任务上的学习能力。

2 背景

本文关注的问题领域是SAT，它是计算机历史上第一个被证明为NP-Complete 的决策问题，它的原始结构文本示例如下所示。

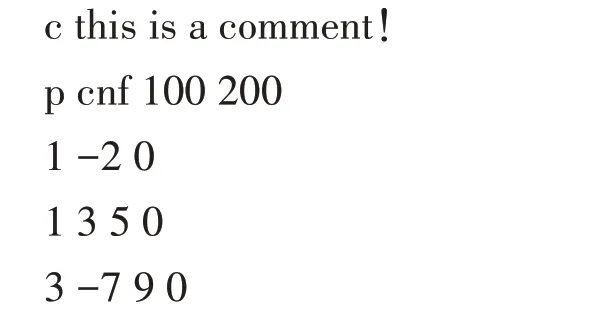
在上例中，以字母“c”的一行表明该行为注释。以“p”开头的一行作为该问题实例的一个简单声明，其中后面的两位数字分别声明了该问题实例有多少逻辑变量和简单析取式，剩余的只包含数字和负号的行都是真正有效的语句（简单析取式），其中以空格为间隔的数字（包括带符号的数字）都是问题逻辑变量的表示，末尾的“0”则是例外，它只是一个结尾占位符，没有任何逻辑意义。从数学的角度来看，比如第三行的数字1和-2分别表示逻辑变量“1”和逻辑变量“2”的逆。每个逻辑变量都可以取真值或假值，每一行中逻辑变量一起组成了一个简单析取式，而所有的语句组合在一起则构成了一个合取范式。SAT 问题的目标就是找出一组所有逻辑变量的具体的真假赋值使得它为真。

算法预测问题都有两个基础的预测模型，即虚拟最佳求解器（Virtual Best Selector，VBS）和单个算法预测器（Single Best Selector，SBS）。VBS 是一个虚拟的理想的预测器，它总是能为每个问题实例选择当前算法组合中最佳的算法，它相当于预测性能的上限，而SBS 只会输出一个算法，该算法可以在问题实例集上取得总体最好的性能，也就是说这是单个算法能够达到的全局最佳性能。

最著名的SAT问题的算法预测器是SATzilla［7～8］，自从第一次在SAT竞赛中取得亮眼的成绩之后，之后的多年该模型一直在不断的发展，并且在实践生产中也得到了应用。近些年来，其他一些优秀的预测模型比如CSHC［9］和ALORS［5］渐渐地涌现出来。无论这些模型的性能如何优秀，用于构建模型的特征一直需要问题专家的精心设计，从而生成可以区别SAT 问题实例的特征模式。这些用于训练模型的特征不可避免地包含着人类的主观性和片面性，它的生成成本也是不可忽略的存在。

随着深度学习的崛起，它也被用于SAT算法预测器的构建［11］，特别是其问题实例特征的自动化。由于原生SAT 问题实例的表示不能直接适用于深度模型，因此该方法还提出了一个基于图像的中间实例。相比于当时最好的预测模型，该模型预测性能还是可以达到不错的性能表型。该预测器主要利用了CNN［13～14］架构，一般来说，基于监督学习方式的CNN 模型都非常依赖于数据样本的质量和样本标签的分布。与众不同的是，算法预测领域的数据集并不是一成不变的，这就导致深度预测模型的性能会受到影响。因此，本文主要研究深度模型在算法预测数据集上的学习能力。

3 数据优化

3.1 数据集扩展

为了能够使用深度学习模型，Loreggia［11］还引入一种问题实例格式转换，它的主要思想是逐个字符地将SAT 问题实例中主要的文本（包括数字，字母，空格和换行符）转换成ASCII 码然后下采样成指定大小的图像，所有除注释和声明行的有效简单析取式都参与了这个的转换过程，一些不重要的SAT 实例文件内容在转换过程中也被移除了，如末尾的占位符号0。对于上述原始SAT 问题示例，三行有效的内容得到的ASCII 代码为49，45，50，48，10，49，51，53，48，10，51，45，55，57，48。此外，由于实例文件中使用的字符个数的限制导致生成的像素值都集中在一个比较小的区间内，于是额外添加了一个从[10，57] 到[0，255]的简单映射来扩展像素值。最终生成的图像对于人来说，直观的反映是一个几乎没有规律的灰度图像。

在训练深度模型时，人们总是期望可以有更多的数据来优化的深度预测模型。但是，由于算法预测中问题域的特殊性，很难收集足够多的数据以生成强大的深度学习模型。SAT 问题的本质是逻辑变量之间的析取与合取，然而最终的合取范式的取值并不受逻辑变量或者简单析取式之间的位置影响［15］。比如简单析取式1 ∨2 ∨3 与3 ∨1 ∨2 在逻辑上是等价的，因此在原始的问题实例内容转换成ASCII 码时，逻辑变量的顺序信息也被编码而加入了图像的信息。总地来说，逻辑变量之间以及简单析取式之间顺序的是可交换的，每个原始SAT问题实例在理论上都可以任意排列和组合这些关键信息，从而可以生成几乎无限的图像格式数据。

3.2 算法标签优化

对于NP 问题的算法，必须提前给定一个运行时间的阈值（截止时间，cut-off time），所以在截止时间内结束计算并得出解的算法就是可用的目标算法。因此，截止时间的预设则显得至关重要，由截止时间的设置引起的算法标签分布的变化会隐式地影响深度学习这类监督学习的模型。

与其他常用的分类任务数据集相比，算法预测任务的数据集普遍存在算法标签不固定的情况（此后的标签就是指算法组合中的算法，不同的实例有不一样的可用的标签/算法）。例如，经典MNIST 手写数字数据集的每个图像有且仅有一个标签，即每张图像都与一个单独的数字相关联。然而，在算法预测相关的数据集中，一个问题实例往往可以被多个算法在指定的时限内完成求解，从而导致大多数问题实例都会对应于多个算法标签。如前文所述，基于CNN 的算法预测研究采用的方法就是这样的分类思想。尽管它也取得了可接受的结果，从问题解决的角度来看，例如，如果基于CNN 的算法预测系统为某个实例选择了排名第五的算法，则至少有五种算法可以解决该问题实例，则问题解决是成功的。但是，从学习算法的角度来看，这样的预测表明该模型并没有在数据集上取得最好的拟合效果，因为它与最优的算法还是很远的距离。因此，算法预测任务在建模时需要尽可能保留原始数据格式里的潜在信息，比如用改变标记策略后的新的算法标签分布作为训练集。为了更合理并简单地区分这些标签分布，原始论文中的标签被称为一般二元标签，其中值1 表示问题实例可以通过特定算法来解决，即运行时间比预设时限更短，反之则为0。此外，由于原始的运行时间数据不太适合直接在神经网络中操作，同时为了与一般二元标签对齐，原来的运行时间可以通过一个映射g(t，T)=(T-t)/T，被压缩成[0，1]。其中，T表示预设的截止时间，t是算法的真实运行时间，1 和0 与二元标签具有相同的意义，但是它们之间的值与1 有着相同的意义，即也可以解决问题实例，只是它们的性能有所不同。这种标签在文中被称为一般连续标签，它本质上是标准化后的运行时间。

如果能够为所有的算法单独确定一个截止时间，因此生成的问题实例算法标签的分布则会与原来的标签分布完全不同。为了研究这种意义上标签分布，本文提出了另一种标签选项，即独立自适应标签。具体的实现方式利用了层次聚类算法（Agglomerative Hierarchical Clustering）［16～17］，独立地对每一个算法在训练问题实例上的性能进行聚类，得到类间距离最远的两个簇：一个表示当前算法能够解决的问题实例，另一个表示余下的“不能被解决”的问题实例。当然，这个“不能被解决”只是表示该问题实例不能在截止时间内被特定的算法解决。这个聚类结果可以导出独立自适应二元标签，对于它的连续版本，则需要根据两个簇之间的边界或相交点的时间作为各自新的截止时间，然后按照一般连续标签的计算方法，生成新的独立自适应连续标签。

4 具体实验

本文中所使用的基本CNN模型来自Loreggia［11］在其论文中使用的深度模型，如图1 所示。由于原始数据集没有公开，所以直接采用了一个开源的ASLib［18］数据库，其中包含大量的各式各样的数据集。本文选取了其中的三个数据集SAT12ALL，SAT12INDU 和SAT0316INDU［19］，它们原始的样本数量分别为1614、1167、2000。此外，SAT12ALL 与SAT12INDU 都有包含31 个算法的算法组合，截止时间都为$1200$，而SAT0316INDU只有10个算法，算法的截止时间为5000。为了消除实验中的随机性，每个实验都会重复运行3次，并且使用5折交叉验证，其中训练集、验证集和测试集的比例为3∶1∶1。实验中，对三个数据集进行增强并获得数据量都彼此接近的问题样本，大约12000 个图像样本，即分别对SAT0316INDU、SAT12INDU 和SAT12ALL扩展6、11、8 倍。在正式训练之前，对所有的图像执行像素值标准化，即让图像的像素值分布拥有零均值和单位一方差。模型优化的目标是交叉熵，优化的方式是随机梯度下降［20］。

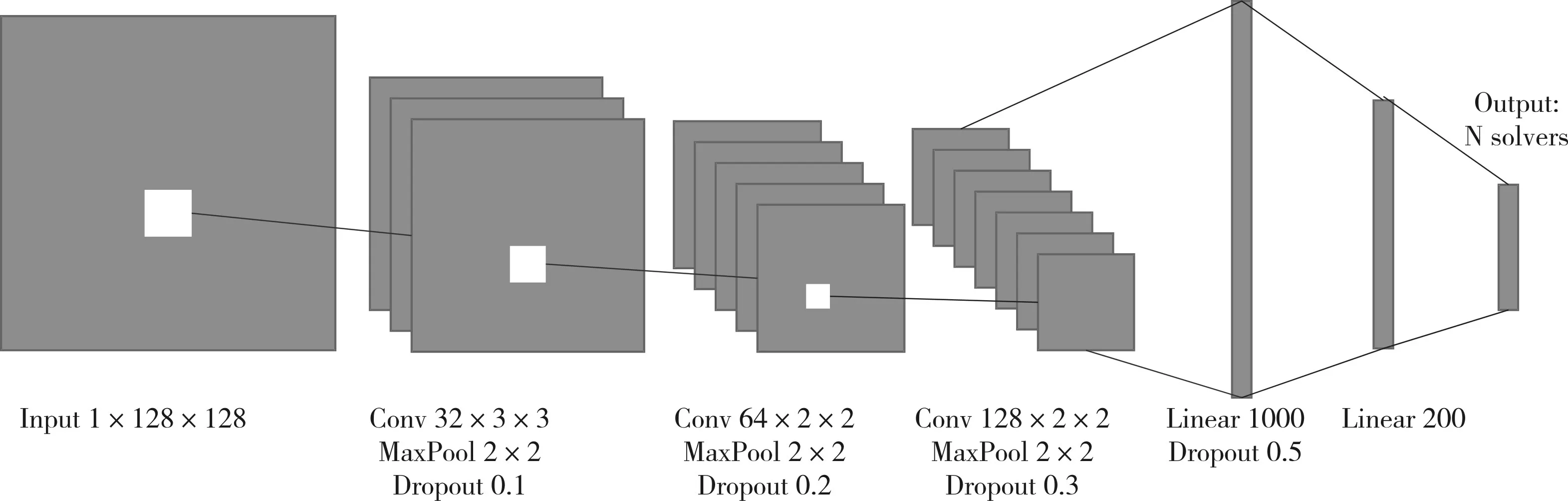
图1 CNN模型结构

评估完成训练的深度模型是该模型走向应用必不可少的一步，然而由于算法预测的问题不唯一的标签的特性，目前主流的算法预测的性能评估都不能公平直观地反映出预测算法的质量。例如，输入一个问题实例，输出排名第一的算法的预测器性能肯定强于输出为排名第三的算法预测器。可以说错误分类损失在一定程度上就是用来衡量算法预测器的预测质量，但是不同的问题实例之间的复杂度可能是完全不同的，直接基于时间的对比就显得不够公平，而且也不能反映出预测器的真实能力。因此，为了更公平且方便地比较算法预测器的预测质量，我们提出了新的评价方法：可解的平均预测算法水平（Solvable Average Algorithm Level，SAAL），见式（1）。SAAL 尝试预测算法a*在当前问题x下实际可行的算法序列Ax中的排名，index函数输出算法a*在其根据算法性能排序的算法列表Ax中的排名，它的取值范围为[0，| |Ax-1]，其中“0”表示预测的算法是算法集中最佳的一个，其他所有不能解的算法的排名输出都是 |Ax|。除此之外，实验中采用的另外一个评估方法是解决率（Percentage Solved，PS），即衡量算法预测器的决策能够解决多少问题实例。在验证模型时，采用的评估方法是带惩罚的平均运行时间（Penalized Average Runtime Score，PAR10），它能表明所有输入实例的期望运行时间。如果预测方法能够解决问题实例，计算时取它的真实值，否则取10 倍的该数据集截止时间。

本文的实验主要测试了同一个CNN 模型在多个不同数据集及其变种上的性能表现，主要由PS和SAAL 测试算法预测器的预测准确性和预测质量，分别记录在表1和表2中。参与测试的预测模型是在验证集上表现PAR10 指标表现最好的一个。此外，在关于未增强的图像集的区域，SAT12INDU数据集没有相关的实验结果，这要归因于SAT12INDU 内部的训练样本太少，导致深度模型在此数据集上的预测效果极其不稳定，因此很淡获得有效的实验数据，这也反映了将深度学习方法应用于算法预测任务的所面临的困难。

表1 多个模型多种数据集上的解决率（PS）

从准确性的角度来看，在SAT12ALL 和SAT0-316 INDU 数据集上的增强图像数据集操作可以显著增加预测模型的解决率，即该操作可以解决更多的问题实例，也可以让无法参于模型训练的数据集能够训练，比如SAT12INDU。在算法标签的选择上，一般二元标签总能够带来最好的预测准确率，但是这并不意味着其它的算法标签没有意义。如表2 所示，以在一般二元标签和增强图像数据集上训练的模型为基础，算法标签优化在一定程度上可以带来更优秀的算法决策，虽然在准确性方面稍微有所下降，但是相对于初始的训练条件，即未增强的图像数据集和一般二元标签，这些优化依然能够带来不同程度的决策质量提升，尤其在SAT0316-INDU 和SAT12INDU 数据集上，模型预测的方法更加偏向于当前问题实例的最优算法。

表2 多个模型多种数据集上的平均的算法预测水平（SAAL）

5 结语

算法预测希望为每个给定的问题实例指定用于求解的最佳候选算法。实践证明，算法预测是一种的有效的组合方法。但是，构建优秀预测模型需要一定水平的专业领域知识。深度学习依靠其强大表示学习功能可以降低这方面的要求。本章主要关注在布尔可满足性（SAT）问题上基于深度学习的算法预测的研究，即问题样本及其算法标签的变化对最终模型的性能的影响，并且提出一个新的评价指标做横向对比。从最后的结果可以看出，将深度学习应用于算法预测的瓶颈依然来自于原始问题数据的重新表示。由于图像已经在下采样的时候丢失了过多的信息，这使得图像很难还原初始的问题实例。另外，人类无法理解图像所表达的含义的缺陷使人们无法进一步探索其学习过程。因此，目前的自动化特征提取亟需找到一种新颖且合理的中间格式来表征复杂的问题实例，从而以较低的代价实现自动化特征的目标。