平行线中的“拐角”

“我”与“你”永远保持相同距离，但又永远不相交，这就是“平行线”。随着平面几何的逐步学习，我越发感觉数学的有趣。譬如我们在学平行线的性质与判定时，有个“经典”图经常出现，我把它归结为“平行拐角”模型。

下面，我们来一起看看它的“庐山真面目”吧！

已知：如图1，AB∥DE，∠B=25°，∠D=30°，求∠BCD的度数。

第一次遇见这题时，我有点“蒙”。老师常说根据条件“顺藤摸瓜”，于是我思考：由已知可以得到什么？由待证或待求的问题思考，还需要什么？可是根据条件“AB∥DE”，无法得出什么，说好的“三线八角”不见了;∠B与∠D既不是同一个三角形的内外角关系，也不是同位角、内错角、同旁内角关系。我一时无从下笔。

没有我想要的，那怎么办呢？对了，那就“变无为有”呗！为什么没有“三线八角”？因为没有与两平行线都相交的“截线”。那好办，延长BC或DC不就行了，见图2（以延长BC为例）。

辅助线一出，我豁然开朗了。

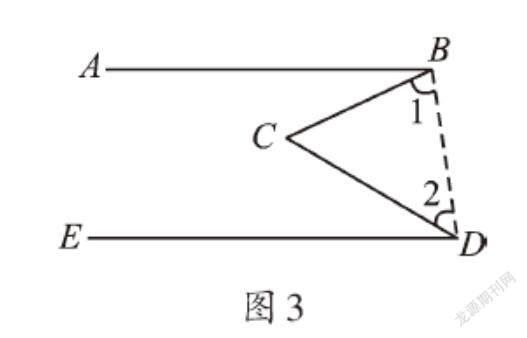
这个“变无为有”的想法一下子打开了我的思路。既然延長BC可以构造内错角，那么直接连接BD不就出现同旁内角了吗？如图3，由AB∥DE，得∠ABD+∠BDE=180°，即∠ABC+∠1+∠CDE+∠2=180°，又因为∠BCD+∠1+∠2=180°，所以∠BCD=∠ABC+∠CDE=55°。

我越来越兴奋了。我由上面这个“∠BCD=∠ABC+∠CDE”结论，又激发出一个灵感。既然∠BCD是两个角之和，那何不“成全”它，把它分成两个角呢？使所分的其中一个角等于∠ABC。相信小伙伴们也想到了吧！对，只要过点C作AB的平行线CF即可，如图4。因为AB∥DE、AB∥CF，所以CF∥DE，所以∠FCD=∠D，结果显而易见了。

向内拐角可以如此，那向外拐角呢？

如图5，已知AB∥DE，∠B=150°，∠D=130°，求∠C的度数。

由之前的启发，我还是“变无为有”，构造“三线八角”，于是几种解法全“蹦”出来了，如图6、图7、图8。剩下的事就是把解题过程完整地写下来，∠BCD=360°-∠ABC-∠CDE=80°。

通过这些辅助线，我发现在图5的情况下，∠B、∠C、∠D三个角之间的数量关系为∠B+∠C+∠D=360°。

那如果调皮的∠C拐到如图9所示的位置，∠B、∠C、∠D又有什么样的数量关系呢？解答思路是否与上面一样呢？这就留给你们了哦！这里，我把老师常说的两句话悄悄告诉你。第一句，“图形发生改变，基本思路不变”;第二句，“创造条件，变无为有”。

教师点评

龚诗凡通过这几道题，给我们呈现了她的一种可视化思维：解决问题时遇到了什么困难，该如何思考，通过什么途径得到“我”想要的，辅助线是如何从“幕后”到“台前”的。小作者向我们娓娓道来，她的思路，相信对于初学几何的同学，一定有所启发。

（指导教师：黄 萍）