考虑渗气渗水函数的非饱和土固结性状研究
陈 聪,张 昭,张同令,赵 伟,刘奉银,齐吉琳
(1.西安理工大学 岩土工程研究所,陕西 西安 710048;2.北京建筑大学 土木与交通工程学院,北京 100044)
1 研究背景
水利工程的建设和运营可能会影响其周边建筑物地基土层的变形及其稳定性,尤以大坝在蓄水后因水环境变化而产生的影响更为显著。以文献[1-2]所述巴西佩雷拉巴雷图市的Três Irmãos土石坝为例,其蓄水过程造成距水库20 km的市区地下水位显著上升,致使地基土层产生明显的增湿变形,从而诱发建筑物沉降破坏。Vilar等[2]对该市区沉降变形量最大的含黏粒砂土层取样开展了持水试验与控制基质吸力的固结试验,结果表明:该地基土层长期处于非饱和状态,因地下水位上升而发生的增湿变形属典型的非饱和土水、气渗流与变形耦合问题。因此,在大坝蓄水对周边建筑物造成的沉降变形分析中,引入非饱和土的一维固结理论及其分析方法至关重要。为此,已有学者采用双变量理论、混合物理论和力-水耦合方法开展了非饱和土固结性状的解析解、半解析解及数值解研究。
(1)双变量理论:Fredlund等[3]以净应力σ-ua和基质吸力ua-uw为基础,结合非饱和土的本构关系与非饱和土的水、气运移规律建立了水、气两相的固结微分方程组。秦爱芳等[4-6]以Fredlund所提固结理论为基础,给出了瞬时荷载和指数型荷载作用时,土层在不同边界及初始条件下的一维固结半解析解。秦爱芳等[7]将迭代法与渗气系数及渗水系数关于基质吸力的函数相结合,求解不同时刻的基质吸力和渗气系数及渗水系数,以分析渗透系数变化时线弹性、黏弹性地基的超孔隙水、气压力随时间的消散规律;陈正汉等[8]和张龙等[9-10]对双应力状态变量进行了一系列推导验证,并在此基础上建立了多种非饱和土固结模型[11-13];Kim等[14]在Fredlund提出的不同循环荷载作用下非饱和土一维固结方程基础上引入两个新变量,并求解出非饱和土在梯形、矩形、三角形荷载等作用下的一维解析解。基于双变量理论的非饱和土固结分析方法通过分析水、气两相的本构关系及其渗流状态,建立了土孔隙内水、气两相运动的控制方程,描述了固结过程中孔隙水压力与孔隙气压力的消散规律。
(2)混合物理论:陈正汉等[15-16]将非饱和土视为互不相融的三相混合物,基于混合物理论导出了非饱和土的水、气渗流规律、土骨架的本构关系及持水曲线方程,构建了三维固结微分方程组,并求解了一维固结解析解及二维固结数值解;苏万鑫等[17]在求解非饱和土一维固结问题时,引入了Bishop有效应力参数,进而分析了有效应力参数、气体压缩模量等参数及流体渗径等因素对孔隙流体压力变化的影响。混合物理论除考虑土的本构关系外,还综合考虑了水、气运动方程、考虑密度变化的持水曲线方程,能够将土体的位移与孔隙水压力及孔隙气压力消散有效的联系起来。
(3)力-水耦合方法:Dakshanamurthy等[18]在非饱和土的固结分析中引入了渗流场与变形场的耦合理论。Wong[19]基于Dakshanamurthy等提出的三维固结方程,假设固结过程中的孔隙气压力恒等于大气压力,仅通过水相连续性原理与土体变形结合,采用有限项方法解方程,开展了非饱和土-水耦合固结的数值研究。李纪伟[20]以非饱和土本构理论和渗流原理为基础,推导了不同初值条件和边界条件下的非饱和土非线性流-变耦合方程组,并求解其显式解析解。Li等[21]基于文献[20]所述固结模型,通过饱和度随时间的变化来反映渗流-变形耦合作用,进而求得渗流-变形耦合方程组的显式解析解。采用力-水耦合方法建立的固结理论,能够通过饱和度的变化来反映渗流场与应力场的耦合关系,近而同时分析土体的渗流与变形规律。
上述表征非饱和土固结性状的解析解、半解析解及数值解研究虽已取得了很多有价值的研究成果,却未将固结过程中的渗气渗水系数比值视为变量,从而忽略了渗气渗水函数对非饱和土固结性状的影响。在非饱和土的实际固结过程中,渗气系数与渗水系数的变化直接影响水、气迁移,这不仅会使基质吸力分布发生变化[22],而且会使三相组分发生改变,这也是非饱和土固结性状分析的关键。因此有必要开展考虑渗气渗水系数比值变化条件下的非饱和土固结解析研究。值得注意的是:文献[7]所述迭代法可求解固结过程中各个时间节点上的渗气系数、渗水系数与基质吸力,但在固结过程的各个时间段中,渗气系数与渗水系数仍为常数,渗气渗水系数比值变化对非饱和土固结的影响仍未考虑;Li等[21]采用离散线性化方法对固结过程中变化的饱和度进行处理,但仅依靠饱和度的联系难以完全反映渗气渗水系数比值变化和持水曲线方程对渗流-变形耦合方程组的影响。为此,本文以非饱和土渗流连续性方程、控制方程及持水曲线方程为基础,构建非饱和土固结微分方程组,采用Li等[21]提出的离散线性化方法将反映水、气迁移相互影响的渗气渗水函数[23-24]代入固结微分方程组,并采用积分变换方法求解方程组的解析解;依据典型算例验证解析解在表征土层孔隙水压力、孔隙气压力时空变化及其沉降变形规律时的有效性。考虑渗气渗水函数的非饱和土固结解析解可用于预测大坝蓄水引起地下水位上升对其周边建筑物产生的沉降变形,评价其整体稳定性。
2 考虑渗气渗水函数的非饱和土固结模型构建
2.1 固结模型的基本假定依据文献[6,15,21],将非饱和土体视为由土骨架、孔隙水、孔隙气体构成的三相多孔介质,分析土体在外荷载作用下的固结性状,并依照如下基本假定:(1)等温条件;(2)土孔隙内的水、气两相在各自压力梯度下的流动服从Darcy定律;(3)不考虑滞回效应;(4)土体呈均质各向同性,仅考虑其线弹性变形,并属小变形、准静态;(5)土孔隙内的水、气两相各自连通,且不承受剪应力,不考虑水、气两相的组分扩散效应和相变;(6)土体变形只发生在一维竖直方向。
基于上述6个基本假定,为分析考虑渗气渗水系数比值变化的固结性状,构建图1所示计算模型及边界条件:假定单一土层处于非饱和状态,取其厚度H,在土层表面施加一均布荷载q,以土层表面为坐标原点,规定沿深度向下为正,取该土层z深度处一微元体为研究对象。

图1 非饱和土层固结计算模型
2.2 水、气两相渗流连续性方程依据基本假定(2)和质量守恒定律,认为由Darcy流动引起的微元体内部流体体积变化等于流入、流出该微元体的流体体积差,即:孔隙水(气)体积变化=孔隙水(气)渗流速度×孔隙水(气)通道断面面积(图1),从而得到水、气两相的渗流连续性方程:
(1)
(2)
式中:Vw、Va分别为微元体内孔隙水与孔隙气体积;Sr为饱和度;qw、qa分别为微元体内孔隙水与孔隙气流量。依据基本假定(2)所述水、气两相运动服从Darcy定律可知:
(3)
(4)
式中:ua为孔隙气压力;uw为孔隙水压力;kw为土的渗水系数;ka为土的渗气系数;γw为水的容重,γa为空气的容重。
又知水、气两相在土中的比例:
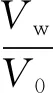
(5)
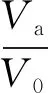
(6)
式中:V0为微元体体积;n为孔隙率。将式(1)—(6)按水、气两相分别联立可得:
(7)
(8)
孔隙率n在固结过程中有如下的变化:
n=n0-εv
(9)
式中:n0为土体在施加荷载前的初始孔隙率;εv为土体在固结变形中的体积应变。由式(9)可得:
(10)
2.3 控制方程表征非饱和土体变形的控制方程主要由物理方程、几何方程和平衡方程构成。其中,非饱和土的应力应变关系可由弹性体的物理方程表示:
σ′=D:εv
(11)
式中D为非饱和土在排水固结状态下的弹性模量矩阵。这里在应力应变关系中引入了有效应力原理,选用Bishop有效应力公式[25]:
σ′=(σ-uaδ)+χ(ua-uw)δ
(12)
式中:σ′为有效应力张量;δ为单位张量;χ为有效应力参数,依据文献[21]近似等于饱和度Sr。
依据基本假定(4),土体的应变和位移之间的关系符合弹性体的几何方程:
(13)
土体内部的应力状态满足平衡方程:
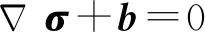
(14)
式中b为外荷载项,联立式(10)—(14)可得:
(15)
在一维固结条件下,将式(15)的张量形式化为标量形式:
(16)
式中:D由张量D降维而得,D=Es/(1-2μ);Es为土的压缩模量;μ为泊松比。
将式(16)与式(7)(8)联立可得非饱和土的水、气两相渗流-变形耦合方程组:
(17)
(18)
2.4 持水曲线方程及渗气渗水函数的离散线性化为描述非饱和土的持水特性对其固结过程的影响,选用文献[26]所述持水曲线方程:
(19)
此外,为考虑渗气系数与渗水系数的变化对非饱和土固结性状的影响,需要补充两个函数关系,即考虑湿度与密度双变化条件下的非饱和土渗透函数[24]及其渗气渗水函数[23]:
(20)
(21)
由式(19)—(21)可知饱和度Sr与基质吸力ψ、渗水系数kw、渗气渗水系数比值kn之间的关系呈强非线性,故而将式(19)—(21)代入水、气两相渗流-变形耦合方程组会使其同样呈强非线性,难以求得其解析解。
为降低渗流-变形耦合方程组呈非线性所产生的求解难度,可采用Li等[21]提出的饱和度区间离散线性化方法实现。具体步骤为:
(1)将给定的某个饱和度区间均匀离散为若干个饱和度微区间段,在每个微区间段中持水曲线的斜率近似为常数,从而将非线性偏微分控制方程组转化为若干个线性偏微分方程组。
(2)至于对线性偏微分方程组的求解,可在给定边界条件与初始条件下,采用积分变换法求得其解析解。
(3)基于叠加原理,将若干个饱和度微区间段内的解析解进行线性叠加,得到该饱和度区间内孔隙水、气压力消散及其沉降变形的解析解。
假定固结过程中的饱和度在Sr1到Sr2的范围内变化,即Sr∈(Sr1,Sr2),将区间(Sr1,Sr2)等分为l个微区间段,如图2所示:
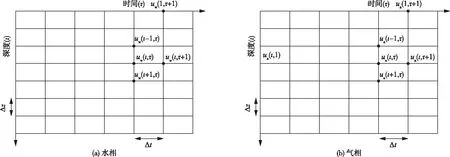
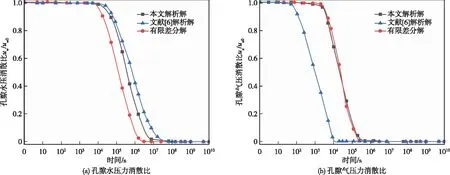
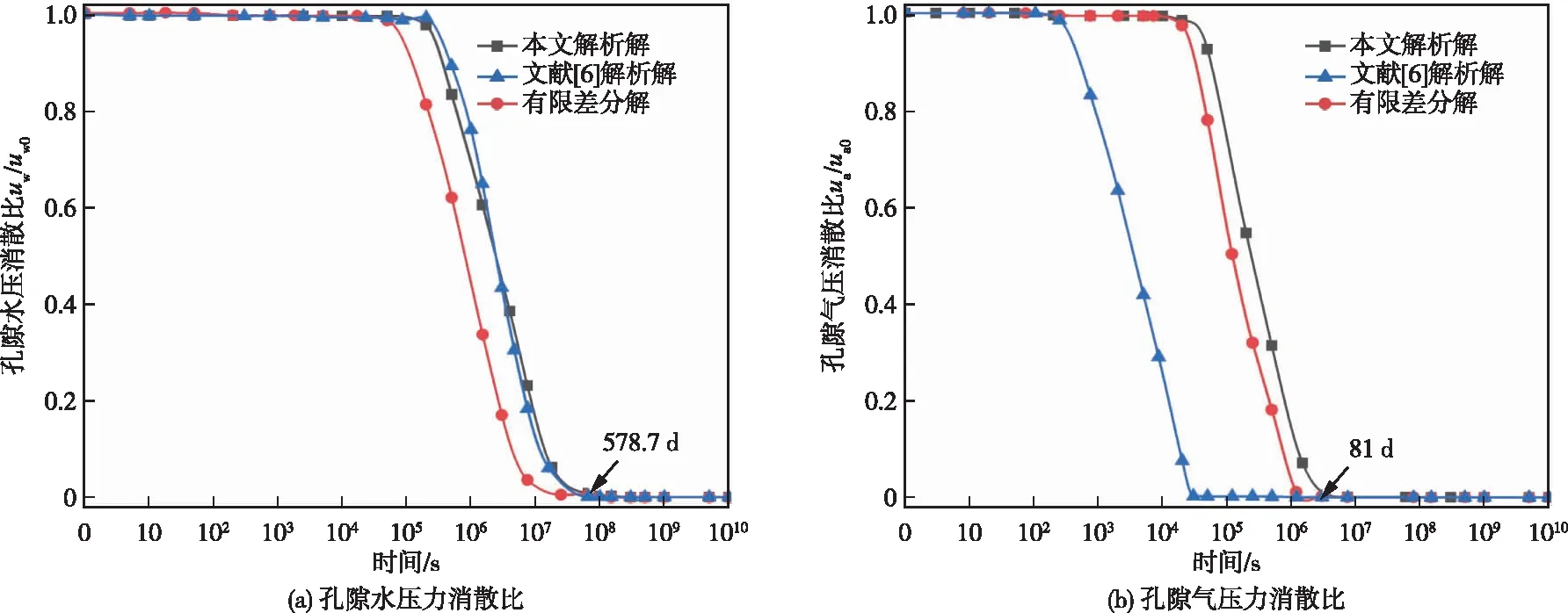
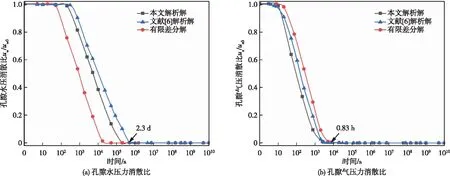
Sr1=Sr1(0) (22) (23) 式中i为第i个饱和度微区间段。持水曲线在该微区间段内的斜率为Fψ(i),考虑到该值在第i个微区间段内变化较小,可取为常数(图2),即: 图2 某个饱和度区间的离散线性化原理示意图 (24) 同理,在第i个饱和度微区间段内的渗水系数kw与渗气渗水系数比值kn可采用相似的处理方法,即: (25) (26) 式(24)—(26)中:Sr(i)为第i个微区间段内的饱和度;kn(i)为第i个微区间段内的渗气渗水系数比值;ka(i)与kw(i)分别为第i个微区间段内的渗气系数与渗水系数;ρd为干密度;a3、a4、a5、b4、b5、b6、m1、m2、p1、p2等均为无量纲的拟合参数。因此,在第i个微区间段(Sr1(i),Sr1(i+1))上取Fψ(i)、渗气渗水系数比值kn(i)、渗水系数kw(i)为常数,并代入式(17)(18)整理后可得 (27a) (27b) (28a) (28b) 2.5 与已有文献所述固结微分方程组的比较本文的固结微分方程组与文献[6,16]所述的固结微分方程组区别如下: (1)文献[6]所述非饱和土一维固结微分方程组为: (29) (2)文献[16]所述非饱和土一维固结微分方程组为: (30) (31) 式(30)(31)所示固结微分方程组除了考虑水、气两相渗流连续性方程、渗透规律及本构方程外,还采用了固相连续性方程、总体平衡方程以及几何方程[16]。因而该方程组在描述了固结过程中水、气两相变化的同时,还能将孔隙水压力与孔隙气压力的消散与非饱和土的固结变形紧密结合。然而,该方程组中的渗水系数kw和渗气系数ka均为常数,这就导致水、气运动对非饱和土固结的影响无法在该方程组中表现出来。 (3)将式(27b)和(28b)分别代入式(27a)和(28a)可得: (32) (33) 本文综合借鉴文献[6,16]所述固结微分方程组的构建方法,将水、气渗流方程、物理方程、几何方程、平衡方程组成渗流-变形耦合方程组。对饱和度进行离散线性化处理,引入饱和度微区间段内的ka(i)、kw(i),从而考虑固结过程中渗水系数kw与渗气系数ka的变化,以反映水、气变化对固结的影响;通过对持水曲线方程离散线性化处理,能够将变化的饱和度与孔隙比代入饱和度微区间段内的固结微分方程组,以同时描述非饱和土固结过程中的土体变形与渗流状态。 3.1 边界和初始条件如2.1节所述,假定一均质非饱和土层位于刚性不透气不透水岩层上,土层厚度为H,其表面瞬时施加均布荷载q[6],土层侧向不发生变形,水和气体只能从顶面排出,则边界、初始条件为: (34) 式中:ua0和uw0为t=0时刻由荷载引起的孔隙气压力与孔隙水压力的初始值,其取值依据文献[27]。 3.2 饱和度微区间段内偏微分方程组的解析解——孔隙水压力ua与孔隙气压力uw的计算式(27)(28)所述的偏微分方程组为固结过程中某一个饱和度微区间段内的固结微分方程组,其形式与文献[16]所述固结微分方程组类似,为简化计算,本文在解析解的求取过程中采用了文献[16]所提的Laplace变换和有限Fourier变换方法。 依据有限Fourier变换的有限正弦变换形式的基本特性可知: (35) (36) (37) (38) 式中H为有限正弦变换的积分范围,aj=(2j+1)π/2H(j=0,1,2,…)。 这里采用Laplace变换如下: (39) 对饱和度微区间段内的方程组采用有限正弦变换和Laplace变换,则式(27)(28)可进一步整理为: (40) (41) 通过解该二元一次方程组得到: (42) (43) 对式(42)(43)采用有限正弦逆变换与Laplace逆变换,得到饱和度微区间段内方程组的解析解: (44) (45) (46) (47) (48) (49) 由式(24)—(28)、式(46)(47)可知,参数C不仅能反映非饱和土中各组分密度与饱和度的变化,而且能够综合考虑渗气、渗水特性,实质上为非饱和土的固结系数。 通过上述的求解过程可知,式(48)(49)仅为固结过程中某一个饱和度微区间段内孔隙水压力与孔隙气压力消散的解析解,对于最终的解析解,还需要通过饱和区间上的线性叠加来得到。 3.3 饱和度微区间段内土层沉降变形量的计算由式(13)与式(16)联立而得: (50) 因此,饱和度微区间段内的土层变形量w(t)可表示为: (51) 将式(44)—(45)代入式(51)可将土层变形量进一步整理为: (52) 3.4 解析解的线性叠加由于2.4节为方便计算对饱和度区间进行了离散线性化,因此,在求得第i个饱和度微区间段内的解析解(式(44)(45)和式(52))后对其进行线性叠加,从而得到固结微分方程组的最终解析解: (53) (54) (55) 3.5 非饱和土固结微分方程组的有限差分解Fredlund等[3]将非饱和土的水、气两相固结微分方程组整理为差分形式的线性方程组,结合大面积均布瞬时加荷所述的边界条件和初始条件,采用迭代法得到了非饱和土一维固结问题的有限差分数值解。本节根据图1所示的非饱和土层固结计算模型,绘制出水、气两相有限差分网格(图3),采用文献[3]所述有限差分方法,将2.4节所推得的考虑渗气渗水系数变化的固结微分方程组(式(27)(28))写成如下有限差分形式: 图3 有限差分法中水、气两相的差分网格 (56) (57) 需要指出:在有限差分计算过程中,采用了式(20)所示渗透函数与式(21)所示渗气渗水函数。 将式(56)(57)整理可得: (58) (59) 式中:ι为深度方向上的距离增量;τ为时间增量; (60) 在具体计算过程中,初始条件和边界条件与解析解一致,同式(34)。由此得到的有限差分解可与3.2节所推得的解析解进行对比分析。 4.1 算例为验证3.4节所推得非饱和土一维固结解析解的有效性,针对一单面的透水透气土层算例,将本文解析解、文献[6]解析解与有限差分解进行对比分析。算例工况如下:取厚度为10 m的土层(沿水平方向向无穷远处延伸),不计土层自重,其上覆均布荷载为q=100 kPa,底部为不透水不透气面,而其顶面可透水透气,固结过程中饱和度的变化范围取Sr=0.45~0.95,该范围内的饱和度微区间段数l=100。固结性状分析中所用土的力学和水力特性参数如表1—2所示(计算参数的设定参考了文献[6,21,23-24,26-28])。 表1 固结性状分析中所用土的力学特性参数 表2 固结性状分析中表征土持水及非饱和渗透特性的拟合参数 4.2 三种解的计算结果对比分析将表1—2所述参数代入本文解析解与文献[6]解析解和有限差分解,求得孔隙水压力与孔隙气压力随时间和土层深度变化的计算结果。为便于分析,取深度z=2、4、6 和8 m,整理出采用本文解析解与文献[6]解析解、有限差分解算得的孔隙水压力与孔隙气压力消散比随时间的变化曲线,如图4—7所示,图中uw/uw0与ua/ua0分别为孔隙气压力消散比和孔隙水压力消散比,描述了孔隙气压力和孔隙水压力的消散程度。 此外,由图4—7可知,本文解析解与文献[6]解析解和有限差分解计算的孔隙水压力与孔隙气压力的时程变化曲线整体趋势一致,表明本文解析解能够反映土孔隙内的水、气两相压力在非饱和土固结过程中逐渐消散、稳定的基本趋势。从图4可以看出孔隙水压力的曲线较孔隙气压力稍平缓,而且土层深度z=2 m处的孔隙水压力于2×105s(即2.3 d)时逐渐消散至稳定(图4(a)),而土层深度z=8 m处的孔隙水压力于5×107s(即578.7 d)时消散至稳定(图7(a))。对于孔隙气压力可以观察到浅层土(z=2 m处)消散至稳定的时间为3000 s(即0.83 h)(图4(b)),深层土(z=8 m处)于7×106s(即81 d)消散至稳定(图7(b)),由此可以看出孔隙气压力的消散比孔隙水压力要快,这一点在图5与图6中也能够发现。 图6 三种解法在z=6 m深度处计算得孔隙水压力与孔隙气压力消散比随时间变化曲线 图7 三种解法在z=8 m深度处计算得孔隙水压力与孔隙气压力消散比随时间变化曲线 在固结的初始时刻(t<100 s时),孔隙水压力与孔隙气压力的消散存在一定时间的滞后。在土层较浅处(图4所示z=2 m处),孔隙水压力与孔隙气压力消散滞后的时间较短。与有限差分解相比,本文解析解的孔隙水压力的消散速率较慢,而孔隙气压力的消散速率略快,这是由于在考虑渗气渗水函数的离散线性化时对饱和度分段的选取较少,计算中使渗气渗水系数比值偏大,也使得表层土的孔隙气压力的消散速率较有限差分解的结果略快;随着土层深度逐渐增大(图5—7所示z=4~8 m处),孔隙水压力与孔隙气压力消散滞后的时间也逐渐增加,可以看出孔隙水压力的消散速率有所减缓而孔隙气压力的消散速率却在逐渐加快,这是由于在土层深处孔隙气压力的消散比孔隙水压力更容易发生,而在土层较浅处孔隙气与孔隙水消散通道之间的相互影响显著,因此孔隙水压力的消散会滞后于孔隙气压力的消散。 图4 三种解法在z=2 m深度处计算得孔隙水压力与孔隙气压力消散比随时间变化曲线 图5 三种解法在z=4 m深度处计算得孔隙水压力与孔隙气压力消散比随时间变化曲线 由于将渗气渗水系数比值视为常数,因此在固结过程中,文献[6]解析解的孔隙水压力消散速率较有限差分解明显变慢,而其孔隙气压力的消散速率较有限差分解明显变快。本文解析解在考虑了渗气渗水函数后,所得到的孔隙水压力与孔隙气压力的消散曲线与有限差分解更为接近。 取两个典型的固结时刻,即t=7.5×102s(即12.5 min)和t=5×104s(即13.89 h),旨在分析固结变形时孔隙水压力与孔隙气压力较完整的消散过程,求得这两个时刻在土层不同深度处三种不同解法的孔隙水压力与孔隙气压力值,如图8—9所示,在某一时刻(如t=7.5×102s(即12.5 min)或t=5×104s(即13.89 h)时)土层发生了一定程度的固结,自土层表面至土层深处可以看出孔隙水压力与孔隙气压力的消散程度逐渐降低:如图8(a)与图9(a)所示在深度z=0处,孔隙水压消散比uw/uw0为0,表明表层土中的孔隙水压力已经完全消散,而在z=8 m处孔隙水压消散比uw/uw0仍接近1,表明在土层底部,孔隙水压力的消散程度较小。同理,在图8(b)与图9(b)所示孔隙气压力的消散曲线中也能看到类似的趋势。 图8 在t=7.5×102 s(即12.5 min)时三种解法计算得孔隙水压力与孔隙气压力消散比随深度变化曲线 图9 在t=5×104 s(即13.89 h)时三种解计算得孔隙水压力与孔隙气压力消散比随深度变化曲线 对比图8(a)与图9(a)所示本文解析解与文献[6]解析解的孔隙水压力消散曲线可知,这两者较为接近,但本文解析解更接近于有限差分解的孔隙水压力消散曲线。对比图8(b)与图9(b)所示本文解析解与文献[6]解析解的孔隙气压力消散曲线可知:由于文献[6]中将渗气系数视为常数,因此,当t=7.5×102s(即12.5 min)时,在土层底部处文献[6]解析解的孔隙气压力的消散程度还很小(其孔隙气压消散比ua/ua0约为0.999),但随着土层变浅,其孔隙气压力消散程度急剧增大(其孔隙气压消散比ua/ua0迅速减小至0);当t=5×104s(即13.89 h)时,在土层底部处文献[6]解析解的孔隙气压力消散比ua/ua0已经减小至不足0.3,随着土层变浅,孔隙气压力消散比减小至接近于0。相比之下,本文解析解在考虑了渗气渗水函数后,所得的孔隙气压力消散程度较小,但在地表处这两种解析解的计算曲线逐渐接近。 此外,由图8—9亦可知,本文解析解计算的的孔隙气压力消散程度高于有限差分解(图8(b)与图9(b)),而其计算的孔隙水压力消散程度低于有限差分解(图8(a)与图9(a))。究其原因在于:本文解析解在考虑渗气渗水函数的离散线性化时,对饱和度分段数的选取会显著影响考虑渗气渗水函数的计算结果,从而使解析解计算的孔隙气、水压力的消散速率与有限差分解产生差异。 4.3 三种解沉降变形的对比计算分析将4.1节中相关参数与4.2节中孔隙水、气压力消散的计算结果带入到式(55)中,整理出采用本文解析解与文献[6]解析解、有限差分解算得的沉降量w与土层初始厚度H之比随时间的变化曲线,如图10所示,非饱和土层在荷载作用下的固结沉降变形随着时间的推移经历了缓慢增长、快速增长、稳定三个阶段。由于在固结过程的初始阶段(t<1000 s时),土层中的孔隙水、气两相在其浅层位置处抢占孔隙消散通道,形成了孔隙水、气压力消散初期的短暂平缓阶段(如图4所示),此时土层的沉降量增幅较缓。然而,在随后的孔隙水、气压力急剧消散阶段(t=1000~7×106s时),由于孔隙水压力的消散滞后于孔隙气压力,因此孔隙水压力的消散速率逐渐加快,此时土层的沉降量也由缓慢增长转为快速增长。当w/H增至1.9%时,土层的沉降变形进入稳定阶段,此时孔隙水、气压力也基本消散稳定,此后的沉降多是由土层蠕变等因素产生的缓慢变形。 图10 三种解计算得沉降量与土层初始厚度之比随时间的变化曲线 由图10亦可知,三种解的计算曲线所描述的非饱和土层沉降变形趋势总体一致。然而,相较于文献[6]解析解,本文解析解的计算结果与有限差分解更为吻合。究其原因在于:本文解析解考虑了渗气渗水函数所反映的水、气渗流相互作用对非饱和土固结变形过程的影响,故而算得的沉降变形曲线更为接近于有限差分解。 本文以混合物理论为基础,在非饱和土的渗流-变形耦合方程组中引入了渗气渗水函数和持水曲线方程,开展了非饱和土固结性状的解析研究,主要得出了以下结论:(1)将饱和度、渗气渗水系数比值和渗水系数进行离散线性化,构建了考虑渗气渗水系数变化的非饱和土固结微分方程组,进而采用Laplace变换和有限Fourier变换求得非饱和土层孔隙水、气压力消散及其沉降变形的解析解。(2)选用水、气两相相互连通的非饱和土层典型算例,对比分析本文解析解、已有文献解析解与有限差分解计算得孔隙水、气压力的消散比随时间与深度的变化曲线,结果表明:因考虑了渗气渗水函数,本文解析解计算的孔隙水、气压力消散速率较已有文献解析解更慢,其消散曲线较已有文献解析解更接近于有限差分解。(3)对比分析本文解析解、已有文献解析解与有限差分解计算得沉降变形与土层初始厚度之比随时间的变化曲线,结果表明:非饱和土层在荷载作用下的固结沉降变形随着时间的推移经历了缓慢增长、快速增长、稳定三个阶段;三种解的计算曲线对这三个阶段的沉降变形趋势描述总体一致;本文解析解因考虑了水、气渗流相互作用对非饱和土固结变形过程的影响,故其沉降变形曲线较已有文献解析解更接近于有限差分解。 本文提出了考虑渗气渗水函数的非饱和土固结解析解,可为大坝蓄水引起的水环境变化诱发其周边建筑物地基沉降变形分析及其整体稳定性评价,提供一种新的计算方法。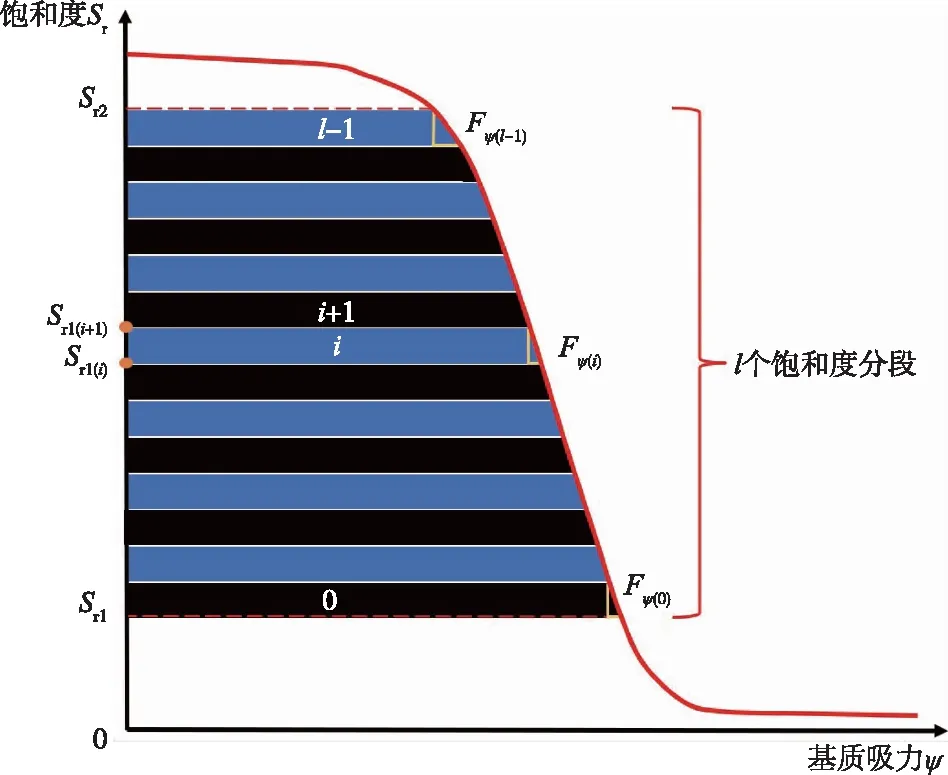
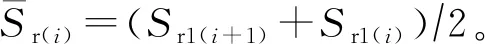

3 固结微分方程组的求解
4 算例、验证与讨论





5 结论

