基于本征正交分解的动边界环形缝隙流场诊断分析

李永业，赵一名，宋晓腾

(太原理工大学 水利科学与工程学院，山西 太原 030024)

1 研究背景

水垫塘、消力池等水工建筑物[1]以及柱塞泵、轴流泵、叶轮等各类水力机械设备[2-3]中往往有着缝隙边界存在，当水工建筑物工作或水力机械运行时这些缝隙中会形成不同类型的缝隙流动。较早的缝隙流动研究方法基于水力学的一元流动理论[4]，将空间三维缝隙边界条件简化为平面二维流动，在有压且忽略彻体力(质量力)条件下引入Navier-Stokes方程与连续性方程按照层流近似求解，再对层流的求解结果进行一系列修正。修正后的一元流动速度分布与缝隙沿流程中部与后部的试验结果吻合程度较好，但在缝隙前部尤其是入口处的结果并不吻合[5]。孙启国等[6]对于同心转子壁面间的环隙流动采用奇异摄动法推导了流场的0阶以及1阶摄动方程并进行了数值求解。这些研究都是基于缝隙流场，以流体运动为研究对象，引入流体运动方程组进行理论推导，并通过边界条件的对称性进行合理简化或应用偏微分方程(Partial Drfferential Equation，PDE)方法数值求解。

上述缝隙流动的研究方法虽然与试验的部分结果吻合程度较好，但是由于在物理模型中采用了一元流动的层流近似，对缝隙流动中存在的不同流层的流体质点相互混掺所引起的附加应力并不进行考量，其参考意义多集中于缝隙流动的速度分布估计以及水力机械的缝隙渗漏量估计[7-8]。除此之外，由于一元流动的定常性，这种层流近似也不能解释缝隙流动的非定常特性，例如湍流脉动所引起的流动结构以及流致振动特征[9-11]。

由于层流近似的缝隙流动研究方法无法研究湍流附加应力，后来出现了直接对缝隙流动非定常特性进行量化的研究方法。其原理是在缝隙流动中监测不同空间点处的压强脉动，根据动水压强与湍流附加应力的相关关系即可定性表示湍流附加应力，并且动水压强的脉动频率就是该空间点处流体振动的频率。李爱华等[12-13]对消力池底板缝隙流动研究中的两种模型进行了对比分析，认为一般缝隙中瞬变流模型较为适用。马斌等[14-15]对异型构造底板缝隙流动从缝隙水流脉动压力的角度分析了键槽的增设对增强底板稳定性的意义。Laima等[16]对双箱梁之间的缝隙流场的涡脱落模式进行了研究，发现缝隙流动中的湍流强度较小时流致振动的幅度较大。孙建等[17-18]研究了水垫塘在排水失效和底板块锚固失效下，底板缝隙的动水压力随底板缝隙宽度及不同止水破坏程度的变化规律。但这种监测动水压力进行缝隙流动非定常特性研究的方法一般只能在壁面处布置测点，所得测量结果并非全流场的结果，并且无法定量描述湍流附加应力。

该研究首次引入了本征正交分解方法对水力机械内具有动边界的环形缝隙流场进行诊断分析[19]，一方面可以对缝隙流动远离壁面处的湍流脉动进行监测，从而量化流场的湍流附加应力；另一方面对本征正交分解的快照矩阵进行时域—频域变换可得到量化流场流体振动特征的功率谱密度函数，这是研究近壁流动非定常特性的较好方法[20-21]。

2 试验方法

2.1 试验系统与测试方法

(1)试验设置：本试验基于囊体管道水力输送系统，囊体为圆柱体，其被运输时受有压管道来流作用在管道内做轴向运动，因此在囊体侧壁与管道内壁之间形成了动边界环形缝隙流场，如图1(a)所示为环形缝隙流场示意图。输送管段为内径DP=100 mm 的平直管段(内半径为RP)，囊体的直径DC分别为60、70、80 mm(半径为RC)，囊体长度为L=150 mm，为保证囊体运动时与管道始终同心，在囊体两侧各添加 3 个直径为 4 mm 的细长圆柱销。该试验设置变量为来流流量与环隙宽度：共设置3个工况流量Q分别为 40、50、60 m3h-1，3 种直径的囊体所对应的环隙宽度分别为B=20 mm(DC=60 mm)、B=15 mm(DC=70 mm)与B=10 mm(DC=80 mm)。使用囊体长度L将环形缝隙流场的流向长度L流向无量纲化，并使用环形缝隙宽度B=RP-RC将环形缝隙流场展向长度L展向无量纲化。流场沿流向(轴向)的速度为w，沿展向(径向)的速度为u，沿侧向(周向)的速度为v。在试验条件范围内，以环形缝隙流场断面平均速度Va为特征速度，以环形缝隙流场宽度B为特征长度确定的雷诺数处于39 000～60 000之间，属于完全发展的湍流状态。

环形缝隙流场由于在周向具有旋转对称的边界条件，类比地球子午面概念，测试时选择以管轴线为轴的一系列通过轴的面作为特征断面，以下简称特征子午面，如图1(b)所示为流场特征断面与几何参数。环形缝隙流场沿流程划分为 3 个部分，分别是前部、中部、后部。物理试验系统如图1(c)所示共分为 5 部分，分别为：首部装置、输送管段、测试管段、尾部装置和循环水箱。其中：首部装置提供稳定的有压流场、输送管段用于连接试验系统各部分进行供水、测试管段用于流场的测试、尾部装置用于回收囊体以及水流、循环水箱用于使系统水流循环使用。流场测试通过粒子图像测速仪系统(PIV)进行。PIV设置参数见表1，其布置如图1(d)所示。

表1 PIV主要参数设置

A.首部装置：1.动力装置，2.调流阀，3.投放装置，4.电磁流量计；B.输送管段；C.测试管段：5.高速摄像机，6.粒子图像测速仪，7.矩形水套(减少激光反射)；D.尾部装置：8.接收装置；E.循环水箱。

(2)试验流程：试验时，先将囊体经过投放装置投入到管道系统内；关闭投放装置使系统密闭、开启动力装置提供有压管道流场；调节调流阀将流量调整至预定工况；待电磁流量计读数稳定后释放囊体。囊体在有压管道流场作用下经历一个短暂加速阶段后达到稳定速度运动阶段；在囊体到达测试管段之前开启PIV系统的激光与PIV高速相机，连续对测试断面进行拍摄得到初始流场数据。当囊体运动到尾部装置后进行囊体的回收，结束一个试验流程。

(3)结果与处理：试验结果分为两部分，一部分为PIV拍摄的流场数据结果，另一部分为其它仪器所测得结果。其中，PIV拍摄结果使用其系统自带后处理程序进行处理：首先将同一工况下的流场初始数据样本进行算术平均处理获取流场的背景边界；其次将该工况所有数据样本减去该背景边界，保留测试断面的缝隙流场数据；再通过Adaptive PIV进行互相关运算(Cross-correlation)；最后将两个PIV相机所拍摄的同一时刻样本进行耦合处理(Stereo PIV)得到缝隙流场平面三维速度矢量。其它仪器所测得结果例如流量、囊体运动速度等通过电磁流量计、高速摄像机等仪器自动处理后直接提取。

2.2 本征正交分解本文采用本征正交分解方法(简称POD)进行研究，该方法最早由J.Lumely引入到流场分析领域，用于寻找湍流中的拟序结构，从而开启了流场模态分析的先河[22]；后经L.Sirvoch改进为使用流场“快照”的实现方式[23]。其分析流程如下所示：

设空间流场的瞬时三维速度矢量集为：

(1)

式中：x，y，z，t分别为流场的空间三维坐标与时刻；i为快照序号i=1，2，…，I；V为该快照下的流场速度。

根据POD降维算法，将流场矢量集合中的所有空间三维流速元素进行降维排列，将降维后的流速元素组合为流场速度矩阵V：

(2)

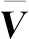
(3)

(4)

其中正交函数φ满足：

(5)

此时问题变为求解特征值方程：

(6)

通过矩阵特征值求解可得到φ和特征值λ，相应的Galerkin投影系数ci为：

(7)

每个特征值占所有特征值之和的百分率即为该特征值所对应的流场模态含有的湍动能相对大小：

(8)

一般在可以捕捉 99% 流场湍动能的前数阶模态处进行截断，模态以其所含湍动能大小进行降序排列，并且假设截断处的模态为第l阶模态，则有前1到l阶模态湍动能相对大小之和η99%捕捉流场99%以上的湍动能：

(9)

各阶模态的流场结构可以写作流场速度矩阵形式：

Vl=cl·φl(x，y，z)

(10)

3 平均流场结果

3.1 流场统计平均特征

(1)如图2所示为统计平均后的特征子午面流场，图2中的流速矢量定性地表征该空间点处的速度方向，各工况流场样本数为500，统计方式为系综平均，并且将流场等分为沿流程的三部分从而进行分析：前部(0～1/3)、中部(1/3～2/3)与后部(2/3～1)，由于不同流量的流场在特征子午面展现的流动特征十分相似，仅有数值等方面的微小区别，因此该部分仅给出流量Q=40 m3/h下，不同环隙宽度时的流场。总体来说，随着沿流动方向的流程增加，垂直于流向同一位置处的速度分布逐渐趋于均匀化，速度幅值有所减小；随着环隙宽度减小，速度幅值明显上升；并且速度场在特征子午面内呈现明显的分区趋势：即在特征子午面前部有一明显的回流区，回流区沿展向向上则是流场内速度幅值最大的主流区。对于特征子午面内的回流区，其类型属于附着于环隙内边界迎流端面的附体运动边界层，或称附着面涡。同一流量时，环隙宽度B越小，回流区流向范围越短，但在展向其范围始终为0～0.3B。

图2 特征子午面平均流场

(2)回流区产生的原因：在作为内部边界的柱体沿流向运动时，在子午面内柱体迎流端面的沿展向的边界与柱体侧壁的沿流向的边界共同构成了一个直角边界，该直角边界阻碍水流的流向运动同时给予了水流展向的扰动，在该直角边界的顶点(柱体的边缘点)两侧是流向速度在展向的突然间断，也是水流展向运动在流动方向受到扰动最大的一点；流向运动的水流在此产生沿径向向外的展向运动速度并与其展向上方不受直角边界直接扰动区域的水流相互作用，水流最终沿着展向与流向之间与流向内边界形成一定夹角的方向运动，使得在水流运动方向与流向内边界之间的流体质点被挟带，压强降低且低于周围区域，引来周围区域的流体质点回流到低压区域，于是形成了该回流区域。

3.2 流场雷诺应力特征

(1)对于湍流流场，雷诺应力可以作为流场各方向对流输运作用强度的度量。对于空间湍流场，雷诺应力可以表示为空间 1 点 3 个方向速度两两之间的二阶相关-ρ·u·v，-ρ·u·w，-ρ·v·w(其中ρ为流体密度；u，v，w为三维流速)，本研究中沿用这一表达形式并通过计算壁面切应力τwall将其无量纲化，具体流程如下式所示。所得展向平均雷诺应力的沿程结果如图3所示，根据PIV设置展向相邻两数据点间隔为0.64 mm。以环隙宽度B为流动的特征长度，并以环隙流场横断面平均速度Va为特征速度[7，9]，那么环隙流动的雷诺数Re与流场的壁面切应力τwall可以分别表示为：

图3 特征子午面沿程雷诺应力

Re=ρ·Va·B·μ-1

(11)

(12)

式中：ρ为流体密度；μ为流体的动力黏滞系数；Cf=0.026Re-1/7为壁面切应力系数。则无量纲化的雷诺应力可以分别写作τuv=-ρuv/τwall；τuw=-ρuw/τwall；τvw=-ρvw/τwall。

(2)总体来说，在各工况下环隙流场的雷诺应力呈现出在流场前部迅速增长、在流场中部维持一定幅值并开始有了下降的趋势、在流场后部，雷诺应力主要趋势为沿程递减。其中主流沿径向的平均对流输运强度τuw远大于同一工况时其它两个方向的平均对流输运强度τuv、τvw，分别高出了6～14 倍、4～7 倍，由此可知在高雷诺数的环形缝隙流场中，主流主要是沿径向进行对流输运，其次是径向流沿周向的对流输运，主流沿周向的对流输运强度相对较小。对于流量Q=40 m3/h时，B=15 mm时的环隙流场 3 个方向雷诺应力最大值都大于环隙宽度B=10 mm以及B=20 mm时的雷诺应力最大值；对于流量Q=60 m3/h时，则是B=20 mm时的雷诺应力较大，B=15 mm与B=10 mm时的雷诺应力相对较小且幅值相近；而对于流量Q=50 m3/h，并无某一环隙宽度时的雷诺应力始终较大。

(3)雷诺应力沿流程呈先增加后降低的变化趋势的原因：特征子午面内流场边界分别沿径向与流向给予来流扰动，而边界条件沿周向近似旋转对称，在周向给予来流的扰动较小，导致雷诺应力中的周向成分占比较低，这也说明对环隙流场简化为特征子午面进行分析较为合理。同时，扰动施加于环隙流场入口并随主流向下游传播，在环隙前部与中部附近增长受到环隙外边界的限制出现最大幅值，再向环隙流场中部及后部传播时，随着离入口的距离增加扰动逐渐减弱。

4 基于POD的流场诊断结果

4.1 流场湍动能贡献分别对不同流量时，不同环隙宽度情况下的特征子午面流场进行本征正交分解。经多次试验研究选定，当每一分解采用 500 张快照、快照时间间隔为 0.002 s时，能够捕捉环隙流场内不同尺度的湍流结构。所得多尺度湍流结构按照脉动能量大小排序，以该流场中总的脉动能量无量纲化所得多尺度湍流结构的湍动能贡献如图4所示，散点表示各模态能量贡献，其坐标值位于图4左侧；曲线表示模态累积贡献，其坐标位于图4右侧。

图4 各阶模态占比与累积贡献

同一流量时的累积模态曲线总是环隙宽度较大的收敛速度较快(B=20 mm>B=15 mm>B=10 mm)。流量Q=40 m3/h时，B=20 mm的前 40 阶模态占流场 99% 的脉动能量，B=15 mm是前 60阶占 99%，B=10 mm是前 80 阶模态占 99%；流量Q=50 m3/h时，收敛速度有所变化，捕捉 99% 流场脉动能量的模态数略有改变：B=20 mm的前46阶模态占流场99%的脉动能量、B=15 mm则是前60阶、B=10 mm是前75阶模态占99%；流量Q=60 m3/h时，B=20 mm时前40阶模态占流场99%的脉动能量，B=15 mm则是前60阶，B=10 mm是前75阶模态占流场99%的脉动能量。如图中散点所示环隙流场各阶模态占比，环隙宽度较大时前10阶模态的占比在同一流量时往往较大，环隙宽度较大的流动其特征长度较大，边界对湍流脉动的限制相对较小，使得湍流脉动有较大的能量。

4.2 流场拟序结构

(1)流场经过本征正交分解后，脉动能量贡献占比较大的模态一般被认为是流场中较大尺度的拟序结构，这些较大尺度的拟序结构决定了流场的湍动形式与湍动分布。图5中给出了流量Q=40 m3/h时不同环隙宽度条件下的前两阶模态时的拟序结构分布，可以代表环隙流场在特征子午面内的较大尺度湍流结构，这些湍流结构在特征子午面内呈现出沿流动方向正负交替的拟序涡形式。不同环隙宽度时环隙流场拟序涡的流向脉动速度幅值范围为 0～2 m/s，展向脉动速度幅值范围为0～1 m/s(B=20 mm、B=15 mm)，0～0.5 m/s(B=10 mm)；流向脉动速度受环隙宽度的影响并不大，但展向脉动速度随着环隙宽度B变小而有明显降低。环隙流场前部到环隙流场中部，拟序涡的特征长度沿流程有着明显的增长(从展向约0.3B～0.5B增长到0.9B～1B)，相邻拟序涡展向特征长度的成长率约为 1.2～1.5，其流向特征长度也有相似幅度的成长；3个环隙宽度工况时的拟序涡在流向与展向都有着不同的变形程度，拟序涡在流向的变形程度B=15 mm>B=20 mm>B=10 mm，在展向的变形程度B=10 mm>B=15 mm>B=20 mm。环隙流场后部，在环隙宽度B=20 mm时有明显拟序涡存在，但B=15 mm、B=10 mm时后部流场已无明显可辨的拟序涡存在，并且此处的脉动速度幅值仅为流场最大脉动速度幅值的 1/10～1/5，说明环隙宽度较小时，环隙流场大尺度拟序结构相对更集中于环隙流场前部以及中部，环隙后部流场随环隙宽度变小，拟序涡更易破碎并耗散。

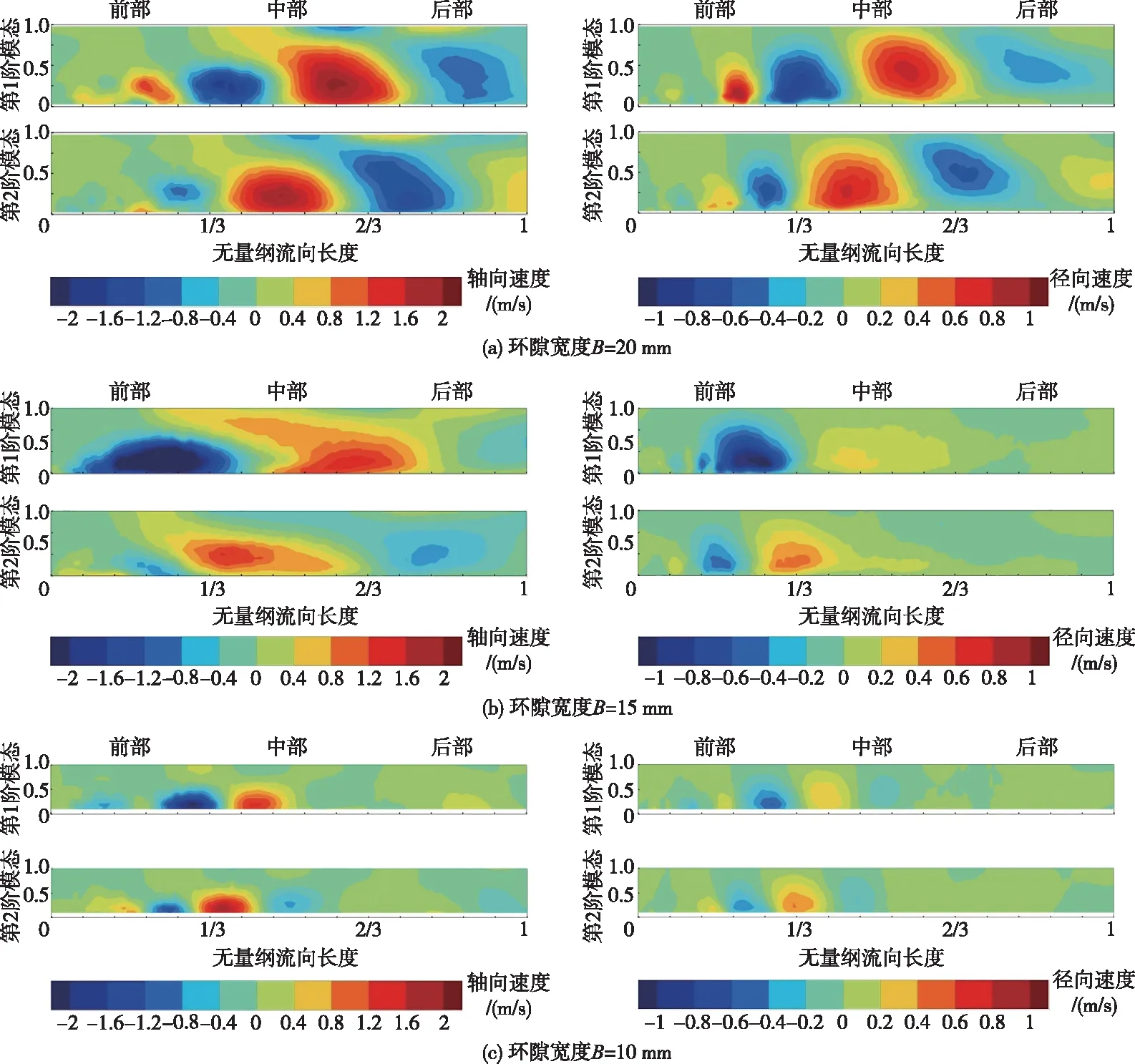
图5 第1阶与第2阶模态的拟序结构(Q=40 m3/h)

(2)环隙流场特征子午面内第一阶与第二阶能量模态占比有所不同，除此之外，前两阶模态的拟序涡形态具有高度的相似性。特征子午面内第一模态的任一可辨识拟序涡，与对应的第二模态内的某一拟序涡形态十分相似，仅是在位置上沿流动方向有所延后并且拟序涡速度方向相反。这一现象与经典圆柱绕流尾迹流场中的前两阶模态现象较为类似：第二模态的拟序涡比第一模态的拟序涡延后半个拟序涡特征长度且速度方向相反，因此可以认为环隙流场中这种现象同样是剪切涡沿流向的产生—发展过程。但该现象与经典圆柱绕流尾迹流场前两阶模态差异在于前两阶模态所含湍动能占流场总湍动能之比相差较大——圆柱绕流前两个模态占比相差十分小，这种差异来源于环隙流场特征子午面内二维边界条件的非对称性导致的模态相对占优。

4.3 流场各阶拟序结构的雷诺应力重构

(1)经过本征正交分解后，湍流流场的各阶能量模态存在的较大尺度拟序结构是导致特征子午面内雷诺应力较大的原因，而较小尺度的拟序结构对流场雷诺应力贡献较小。通过对每个模态计算沿程平均雷诺应力以得到不同工况时某一模态在流场沿程各处的雷诺应力贡献，对流场的对流输运进行尺度分离。如图6所示即为流场主流沿径向的平均雷诺应力沿程分布曲线、对应工况的前5阶模态雷诺应力贡献曲线以及前5阶模态总和雷诺应力贡献曲线。各个工况时，前5阶的流场模态已经能够捕捉流场60%～80%的雷诺应力，对于能量累积贡献曲线前5阶流场模态只能捕捉50%～70%的流场能量，对比可知一方面流场的雷诺应力主要来源于流场内较大尺度的湍流脉动，另一方面流场的前5阶模态对雷诺应力贡献要比对流场脉动能量贡献略大。

图6 低阶模态沿程雷诺应力贡献曲线

(2)随着环隙宽度的减小，主流沿径向的雷诺应力持续减小，说明主流的径向对流输运愈加受到边界的限制。第 1 阶与第 2 阶模态贡献的雷诺应力远大于第 3、第 4、第 5 阶模态，约为 20～40倍。并且前 5 阶模态雷诺应力的峰值，尤其是前两阶模态的雷诺应力峰值与流场平均沿程雷诺应力峰值较为对应，而前 5 阶模态的累积雷诺应力曲线与平均沿程雷诺应力曲线十分相似并且在沿程某些位置处幅值相等。经过计算，前 20 阶模态所对应的累积雷诺应力曲线已与平均沿程雷诺应力曲线较为符合，最大相对误差不超过 5%；前 50 阶模态相应的最大相对误差不超过 1%，说明采用本征正交分解所得的低阶能量模态分别计算雷诺应力再线性叠加即可很好地估计平均流场的雷诺应力。

(3)本征正交分解的前数阶模态能够对统计平均的雷诺应力进行较好近似的原因在于：本征正交分解的各阶模态是按照瞬态流场若干种流动状态时湍流结构的脉动能量大小进行降序排列。前数阶模态脉动能量最大的同时也说明这些模态具有相对其它阶模态较强的动量输运能力。3.2节中统计平均的流场沿程雷诺应力为所有湍流结构的动量输运结果，不仅包含对动量输运贡献较大的较大尺度的湍流结构脉动，同时包含了对动量输运具有极小贡献的具有微尺度的各向同性湍流脉动。但是工程研究更关注较大尺度的湍流结构，并且根据各模态雷诺应力曲线峰值的位置可以判断不同模态的动量输运形式，因此使用本征正交分解的前数阶模态对雷诺应力进行重构比直接对流场雷诺应力统计平均计算对流场具有更强的解析能力。

4.4 流场振动的频域特征(1)由于本征正交分解中速度被写作全场任一点的相关函数形式，可以通过时域-频域变换求得其功率谱密度[19]。如图7所示为由本征正交分解所得的前若干阶模态(捕捉到 99% 湍动能的前数个模态)的时间系数加矩形窗并所进行快速傅立叶变换(FFT)所获得的流场全场的功率谱密度曲线，可以在一定程度上反映流场湍流脉动的频域特征，一般认为：较大的湍流结构使得自相关函数较大，对功率谱密度的贡献更大[20]。总体而言，同一环隙宽度在不同流量条件下的频域分布较为相似，在较低频率的区域振幅(功率谱)较大，在较高频率的区域振幅(功率谱)较小，两者之间相差10到100倍。(2)由各PSD曲线在不同频率段的功率谱相对大小可以将环隙流场的湍流脉动频域分为三个子区：低频段、中频段、高频段，其中低频段在频域约为 0～10 Hz，由于在相同流量下环隙流场湍流特征长度——环隙宽度变小，其较大尺度湍流脉动受到边界的约束作用导致功率谱较小；中频段在频域约为10～120 Hz，此时环隙宽度较小的环隙流场功率谱相对较高，湍流脉动长度尺度不再主要受到环隙宽度的限制从而具有相似的湍流特征长度，此时在环隙宽度较小的环隙流场中流动的特征速度较大，因此该频率段的湍流脉动在宽度较小的环隙中更强；到了高频段 120 Hz 以上，湍流特征长度与流动特征速度都不再是影响湍动功率谱的主要因素，此时所余下的是高频的混乱无规则小尺度湍流，其总体的功率谱随着环隙流场宽度变窄而降低。(3)环隙流场的功率谱密度函数的分区特征原因主要在于：低频段代表的流场最大尺度脉动受到环隙宽度的限制程度随着环隙宽度减小而变强，表现为功率谱(振幅)的减小，限制了大尺度脉动从主流中获取能量；中频段反而是随着环隙宽度减小功率谱增大，该区域主要作用是从大尺度脉动获得能量向微尺度脉动传递，因此大于该频段尺度的较大尺度脉动的尺度越小，这种传递作用就越容易发生；而到了高频段，由于环隙宽度较小时脉动本身具有的功率谱较小，因此相对于环隙宽度较大的工况衰减较为严重。

图7 环隙流场累积功率谱密度曲线

5 结论

(1)首先环形缝隙流场的平均流动随着环隙宽度的减小其速度幅值明显上升；其次速度场在特征子午面内呈现明显的分区趋势：前部有一明显的回流区，其沿展向向上则是主流区。流场前部的雷诺应力迅速增长、在流场中部维持一定幅值、在流场后部迅速沿程递减。主流沿径向的平均对流输运强度大于同一工况时径向流沿周向的对流输运强度4～7 倍，大于主流沿周向的对流输运强度6～14倍。(2)湍流结构在特征子午面内呈现出沿流动方向正负交替的拟序涡形式。不同环隙宽度时环隙流场拟序涡的流向脉动速度幅值范围为 0～2 m/s，展向脉动速度幅值范围为 0～1 m/s(B=20 mm、B=15 mm)，0～0.5 m/s(B=10 mm)；流向脉动速度受环隙宽度的影响并不大，但展向脉动速度随着环隙宽度B变小而有明显降低。环隙流场前部到环隙流场中部，拟序涡的特征长度沿流程有着明显的增长(从展向约 0.3B～0.5B增长到 0.9B～1B)，相邻拟序涡展向特征长度的成长率约为 1.2～1.5。(3)环隙流场的前数阶模态代表了流场内较大尺度脉动的湍流结构，其所具有的动量输运强度较大、雷诺应力幅值较高。其中，前 5 阶模态可以捕捉到平均流场 60%～80% 的雷诺应力；前 20 阶模态可捕捉 95% 以上的雷诺应力。并且不同阶模态的贡献曲线反映了各模态时动量输运的峰值位置，使用低阶模态对雷诺应力进行重构可以较好的估计流场的雷诺应力。(4)功率谱密度函数表示的流场流致振动频谱在同一流量时有着较为明显的分区趋势。对于低频段(0～10 Hz)与高频段(120 Hz 以上)环隙宽度较小时功率谱密度较大；对于中频段(10～120 Hz)则是环隙宽度较大时功率谱密度较大。对于环隙流场，环隙宽度的减小对于其较大尺度的流致振动抑制作用较强。