复合固体推进剂双螺杆挤出成型过程DEM-CFD 耦合仿真

王 建，刘 皓，赵亚风，乔晓林，李兴刚，赵 慧

（1.北京化工大学机电工程学院，北京 100029；2.北京航天试验技术研究所，北京 100074；3.西安航天化学动力有限公司，陕西 西安 710025）

1 引言

双螺杆挤出成型是火炸药柔性制造的核心技术，具有连续生产进而提高生产效率、减少工艺环节进而提高安全程度等优势［1-2］，在固体推进剂生产中的应用将改变传统生产模式。近年来，数值模拟技术在火炸药螺压挤出加工生产过程中应用日益突出［3-5］，在安全可靠性方面可发挥重要作用。但是，由于火炸药组分的复杂性，相关模拟技术［3-5］均把火炸药物料体系简化为流体，且只选取了部分较短螺杆结构进行模拟，仿真模拟的精度仍然很差。复合固体推进剂以铝粉和高氯酸铵氧化剂为主要组分［6-8］，由于固体颗粒含量较多，通过单纯的计算流体力学（CFD）的模拟方式难以确保计算精度。复合固体推进剂的过程仿真必须考虑固态颗粒的运动规律。离散单元法（DEM）可实现颗粒散状物料性质的有效表征及其加工生产过程的可靠仿真［9-10］。DEM 与CFD耦合可实现复合固体推进剂的过程仿真，并能获得更高的仿真精度。目前，随着ANSYS 等计算机辅助分析软件的发展，DEM 与CFD 耦合仿真在工业界得到了广泛应用［11-14］，但用于火炸药的双螺杆加工过程仿真的报道仍然很少。因为复合固体推进剂的双螺杆加工生产过程仿真不但需要考虑物料颗粒的特性以及流体相的流动特性，还要考虑固液两相之间的关系，通过DEM 与CFD 耦合实现复合固体推进剂加工过程的仿真仍然难度较大。

为了推动DEM 与CFD 耦合技术在固体推进剂双螺杆加工生产过程仿真中的应用，针对以铝粉和高氯酸铵氧化剂为主要组分的复合固体推进剂，采用DEM仿真与安息角测试相结合的标定技术［15-17］获得铝粉、高氯酸铵及其颗粒混合物的接触模型参数，通过流变测试实验确定液相的黏度模型参数，采用DEM 与CFD耦合实现复合固体推进剂双螺杆挤出成型过程的仿真。相关方法与结果可为固体推进剂的生产加工过程提供技术参考，为设备结构与工艺条件的进一步优化和生产工艺的安全可靠性评估提供理论支持。

2 试剂与仪器

复合固体推进剂的固相颗粒物主要由铝粉和高氯酸铵按质量比1∶2 组成；复合固体推进剂液相某比例混合物，西安航天化学动力厂提供。复合固体推进剂由固相颗粒和液相混合物按质量比5∶1 混合组成。

黏度计，型号Haake RV1，美国赛默飞世尔科技公司生产。

液体控温循环器，型号Haake P1-C35P，美国赛默飞世尔科技公司生产。

3 实验部分

对固体推进剂中添加的液相混合物进行了黏度测试。设定温度窗口为10～70 ℃，测定混合液体的黏度变化。采用Z31 转子，Z43 转筒，装入液体50.5 mL，为转筒体积2/3。降温及加热过程通过液体控温控制器控制，升温速率2 ℃·min-1，测温点保温30 min，温度精度为±0.1 ℃，定剪切速率0.1 s-1。图1 显示了复合固体推进剂液相混合物的黏度随温度的变化曲线。随着温度的升高，物料的黏度下降。在仿真计算时，假设液相为牛顿流体。结合实际生产工艺，取温度40 ℃时液相混合物对应的黏度值1.78 Pa·s 用于DEM-CFD耦合仿真。

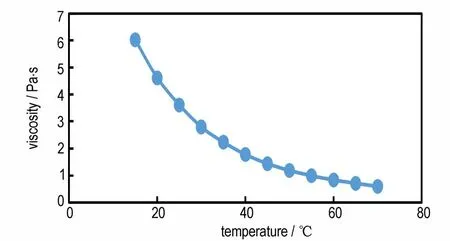
图1 混合液体的黏度变化Fig.1 Mixed liquid viscosity changes with temperature

4 模拟仿真

4.1 DEM 仿真

（1）几何模型

仿真计算的几何模型为双螺杆装配模型，包含机筒、两根螺杆以及进料口。机筒一端为开口状态，进料口和出料口（机筒开口）为常压口。双螺杆中心距43 mm，螺杆外径为52 mm，由螺纹元件、啮合元件组成，依次包括三块螺距64 mm 的螺纹元件、一块螺距32 mm 的螺纹元件、三组60°错列角厚32 mm 的啮合元件、五块螺距32 mm 的螺纹元件、一块螺距32 mm的反向螺纹元件，总长512 mm，如图2a 所示。螺杆之间的间隙以及外螺纹与机筒之间的间隙均为1.2 mm。补充几何平面约束来完善DEM 中模型的处理，如图2b 所示，添加标红的平面作为密封面，添加标红无底长方体盒子作为颗粒工厂。根据工艺参数定义螺杆几何体转动轴及转动方向与转速。研究中涉及两根螺杆的同向转动，过大的网格数量使计算机负荷增大，最终确定用于计算的螺杆网格尺寸为2 mm，总网格数721548。图2c 显示了螺杆网格划分情况。

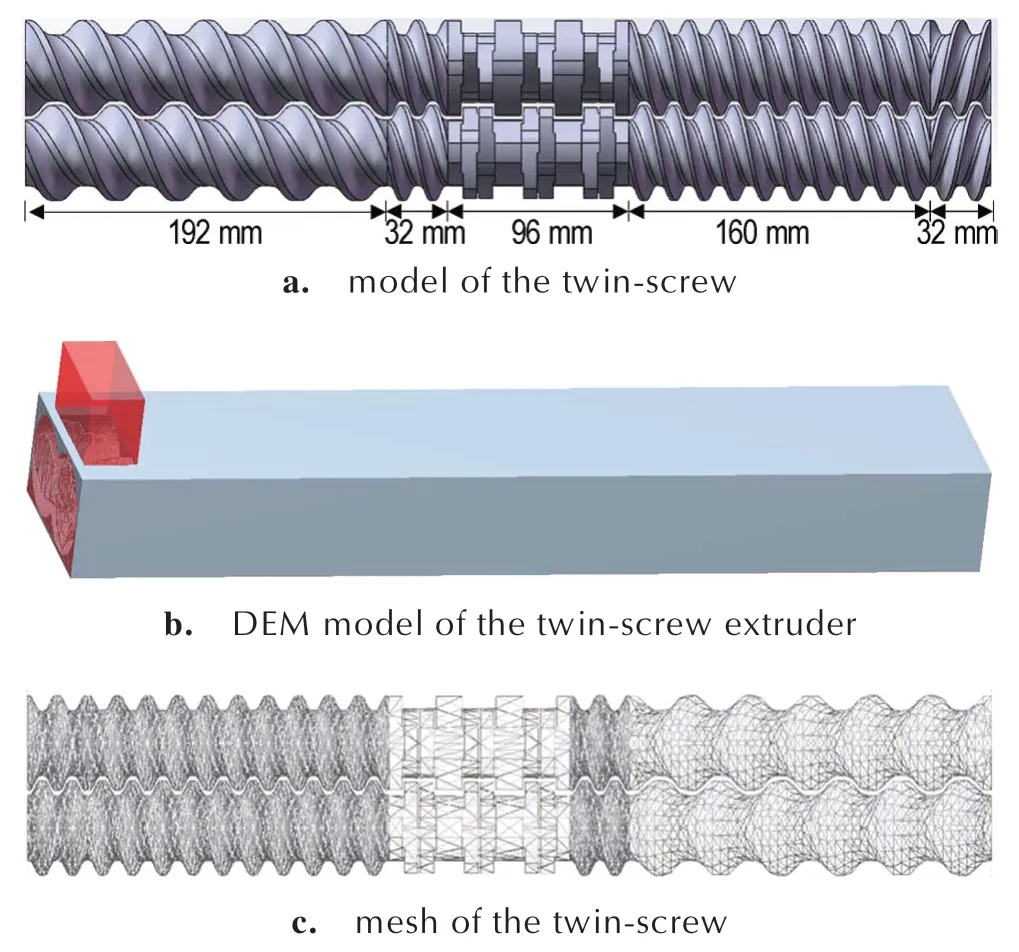
图2 双螺杆挤出机构模型Fig.2 Model of the twin-screw extruder

（2）物料模型

铝粉颗粒泊松比为0.3，密度2700 kg·m-3，剪切模量2.6×1010Pa；高氯酸铵颗粒泊松比0.4，密度1500 kg·m-3，剪切模量1×108Pa。物料模型中包含多种颗粒模型，离散元计算的基础是颗粒的运动。需要对颗粒形状和大小等进行定义。将颗粒定义为球形颗粒，标准颗粒半径为0.1 mm，考虑到真实的铝粉和高氯酸铵颗粒直径分布不均匀，设置颗粒工厂中粒径在一定范围内随机产生，最大粒径为0.3 mm，最小粒径为0.02 mm，在颗粒工厂中的随机位置产生。物料最适宜的表面能为5 J·m-2，相关用于DEM 分析的接触模型参数如表1 所示［18］。

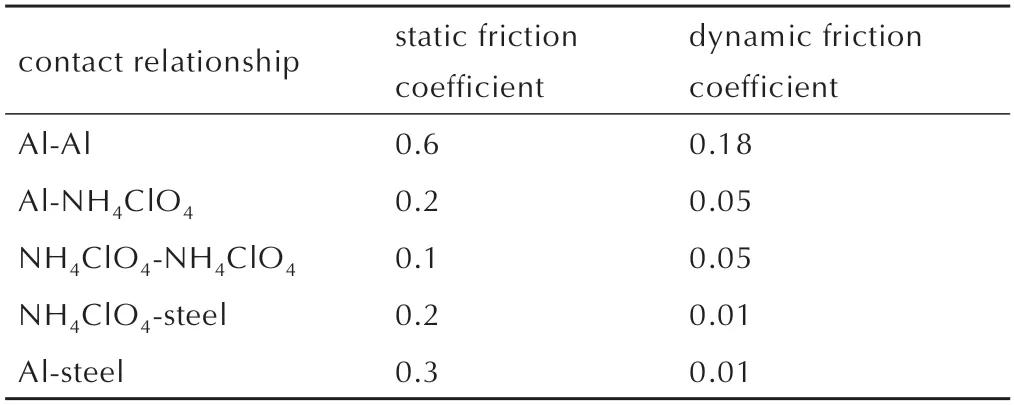
表1 接触模型参数Table 1 Parameters of the contact model

（3）DEM 仿真控制方程

考虑到研究对象为高固体含量的推进剂，认为材料混合后固体颗粒被包裹在胶体之中，颗粒与颗粒之间的作用力不仅存在于法向作用力，也有较为明显的切向作用力。Hertz-Mindlin with JKR 模型［20］优势在于存在法向力以及切向粘结力，无论对于前期的粉体料混合过程还是后期加入凝胶后的浆体推进剂，Hertz-Mindlin with JKR 模型均可较好的解释实际固体推进剂的物理行为。因此，选择DEM 中Hertz-Mindlin with JKR 模型作为颗粒接触力模型。模型的法向作用力取决于颗粒之间的重叠量和表面能，且存在式（1）关系：

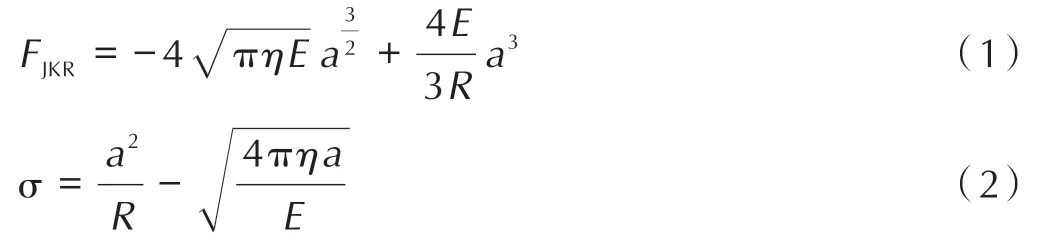
式中，FJKR为法向作用力，N；E为杨氏模量，Pa；R为当量半径，mm；a为接触半径，mm，此处与物理半径保持一致；σ为颗粒重叠量，mm；η为表面能，J·m-2。

Hertz-Mindlin with JKR 模型提供了吸引凝聚力，即使颗粒并不是直接接触，颗粒间仍然存在非零凝聚力的最大间隙为σ0，可以通过式（3）计算：

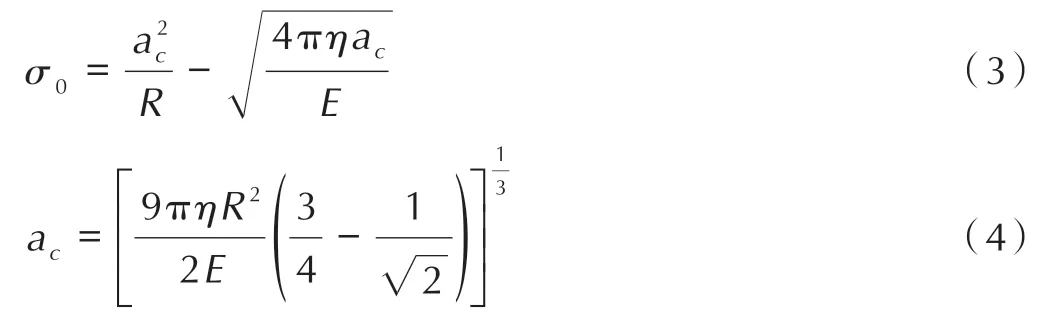
式中，σ0为存在凝聚力的最大间隙，mm；当σ0＜σ时，模型计算返回值为0，此时物料颗粒之间距离过大，不存在凝聚力。

（4）工艺参数设置

根据实际生产情况，螺杆转速统一设置为70 r·min-1，两根螺杆同向转动。在DEM 固体颗粒输送仿真过程中，铝粉与高氯酸铵质量比为1∶2 进料，颗粒按质量流率生成。设置了5 组不同喂料量的实验，如表2所示。

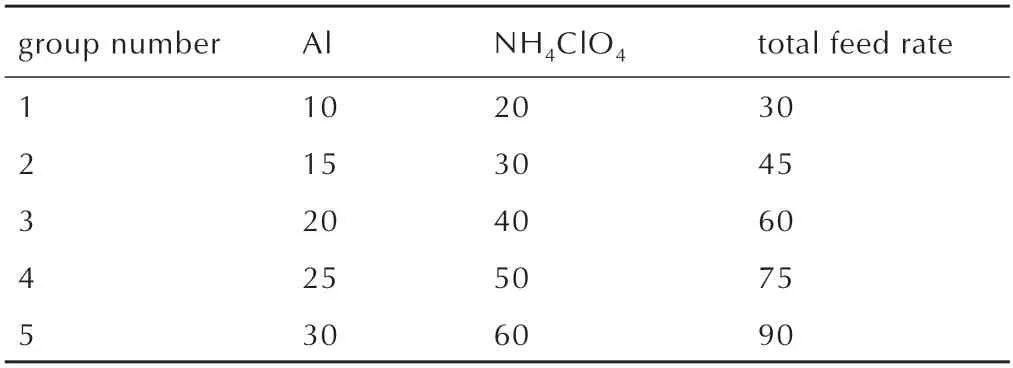
表2 颗粒喂料量设定Table 2 Feeding rate of the powders kg·h-1

（5）求解器设置

考虑后续与CFD 软件耦合时时间步长之间的联系，将设定时间步长为2.5e-07 s，计算得到瑞利时间步长的22.9%。经过多次试算，在螺杆转速70 r·min-1时，经过15 s，颗粒可以从右侧出料口挤出，再经过5 s之后发现颗粒的运动分布情况以及基本趋于稳定，最终设定总时长20 s 进行仿真计算。

4.2 CFD-DEM 仿真

（1）模型与网格划分

DEM-CFD 耦合仿真中对筒体内壁面、进料口、出料口、螺杆区域进行面划分，对流道区域采用填充的体网格划分，总网格数483002，网格模型如图3 所示。因为计算工作量问题，CFD 模拟采用的螺杆模型只选取了螺纹输送段和啮合段，省去了DEM 模拟中啮合段之后的输送段。采用动网格Porfile 文件指定网格运动。由工艺条件设定螺杆转动速度与DEM 设置相同，为70 r·min-1。利用Profile 文件中的表示角速度的语句定义，采用瞬态方式，取时间0、0.1、1000 s 三个数据点，三个数据点沿x轴转速均为7.33 rad·s-1。代表其匀速运动，无转动加速度。

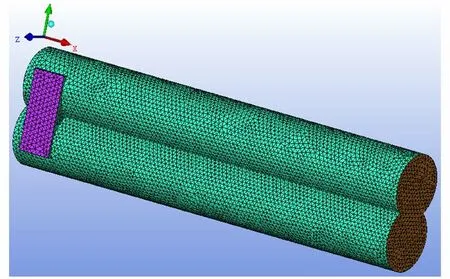
图3 DEM-CFD 仿真螺杆网格划分Fig.3 Screw mesh generation in DEM-CFD

（2）DEM-CFD 耦合仿真控制方程

颗粒流与流体进行耦合计算的主要模型有两种：拉格朗日（Lagranginan）模型和欧拉（Eulerian）模型。两种模型的选择主要取决于固体含量的多少。拉格朗日模型中只包括固液两相之间的动量交换，通常在固含量低于10%时选用该模型。对于本研究中复合固体推进剂，固含量为85%，故采用欧拉模型。欧拉模型考虑了固液间的动量交换以及固体颗粒对于流体流动状态的影响。欧拉方程是拉格朗日方程的修正方程，在描述耦合模型时在控制方程中添加流体体积分数φ，当φ=1 时，模型为拉格朗日模型，物料中无固相存在，当φ＜1 时，模型为欧拉模型。耦合后，流体相满足连续性方程及动量守恒方程，颗粒系统则遵循牛顿第二定律。

流体连续性方程为：

动量守恒方程为：

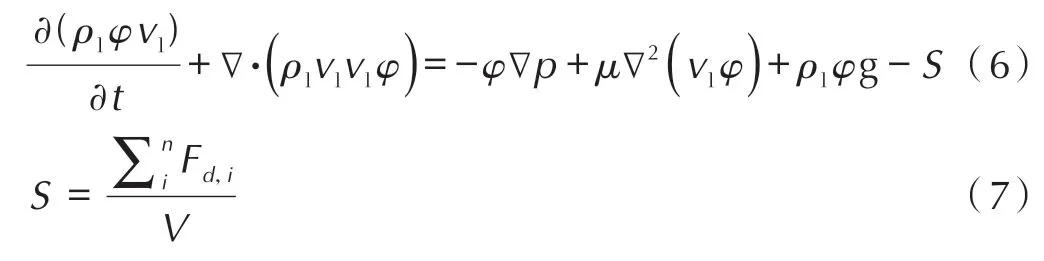
颗粒运动方程满足：

式中，ρl为液体密度，kg·m-3；φ为液相体积分数；vl为液相速度，m·s-1；g 为重力加速，9.81 m·s-2；p为压力，Pa；μ为液体黏度，Pa·s；S为两相动量交换源项，kg·m·s-1；V为CFD 网格单元体积，m3；Fd，i表示作用在网格单元的流体阻力，N；∑F为颗粒所受的合力，N。

（3）耦合计算条件

首先设置DEM 模型以及物料参数，通过读取UDF 耦合文件进行耦合。DEM 与CFD 软件进行耦合后，CFD 软件自动读取DEM 中的各项参数作为计算参数。计算方式为瞬态计算，重力设定为z轴9.81 m·s-2，与DEM 中设定保持一致。螺杆转速为70 r·min-1，流体进入流量设定为15 kg·h-1，固体颗粒进料质量流量设置为75 kg·h-1。出口设置为常压出口。温度设定为40 ℃，流体粘度为常数黏度1.78 Pa·s，密度为920 kg·m-3。

求解器设置主要注意时间步长。耦合计算需要根据DEM 中的求解器关联设置，CFD 耦合计算时的时间步长为DEM 计算时间步长的100 倍，最大迭代次数为40 次，总时间步10000 次。

5 结果与讨论

5.1 DEM 模拟结果分析

（1）总进料量选择

在DEM 模拟中，设置五组混合进料来判断颗粒工厂产生颗粒的适宜的喂料速率，分别为30、45、60、75、90 kg·h-1，螺杆转速均为70 r·min-1，其它颗粒属性设置与计算边界条件设定都相同，物料填充结果如图4 所示。图4a 中，物料主要分布在螺杆的机筒壁面以及螺杆啮合处，综合图4a 中的粒子分布，不难发现此时进料量过低。分析图4 中物料分布，低喂料量进料情况下，固体颗粒在进料过程较为分散，表现为小颗粒的局部团聚，物料整体不连续。这是由于物料进料量过低，颗粒较少，多数颗粒与颗粒之间距离较大，远远大于JKR 计算模型中存在粒子间粘结力的最大距离［20］。另一现象为物料容易沉降在机筒底部，运动缓慢。这是由于物料受到重力作用的影响，与周围颗粒粘结后沉降在螺杆底部，而颗粒的堆积高度小于螺杆与机筒之间的间隙，螺杆的旋转产生的对物料的推动力、摩擦力、剪切力等无法作用到团聚的颗粒上。只有在堆积高度大于螺杆与机筒间隙时才会有一小部分向前运动。这也是靠近进料口的物料明显多于靠近出料口的螺杆段的物料的原因。图4b 与图4c 中，物料随着进料的增加在螺杆上分布有了较大改善。图4d 与图4e中进料口都存在物料堆积，满足了颗粒之间相互接触、连续进料的要求。鉴于过大的进料会给设备造成较大的负荷，因此最终选用的适宜固体颗粒进料量为75 kg·h-1。

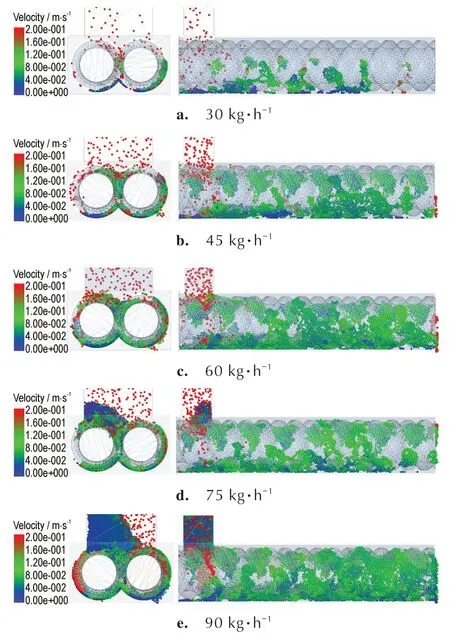
图4 不同颗粒喂料量条件下在4 s 时刻的物料颗粒分布Fig.4 Material powder distribution at 4 s for different feeding rate of powders

（2）颗粒分布

为确保固体推进剂双螺杆挤出成型过程仿真在DEM 中的正确性，将仿真结果进行处理。分析了达到稳定状态时候，物料在双螺杆中的分布状况如图5a 所示。耿孝正［19］在1993 年研制成功国内第一台可视化双螺杆挤出实验装置，通过此装置做了固体粒料的双螺杆输送实验，图5b 为螺杆粒料输送的实际分布情况。观察仿真结果图5a，红框区域分别与图5b 中视角对应，可以发现DEM 仿真计算的结果与耿孝正聚丙烯颗粒料输送结果描述的分布情况相符。在上输送区内物料聚集，在左输送区内物料堆积偏左下方堆积。由于螺杆的上旋，旋转的螺杆对物料的摩擦拖拽，使得物料有上爬行为。当重力大于摩擦力时，物料下滑，最终在斜面位置保持平衡。螺杆的正右侧方向基本上看不到物料，右输送区的物料运动在下啮合区处，在机筒隆起的部受阻。DEM 仿真结果与可视化双螺杆固体混合试验结果吻合，证明了DEM 仿真结果的正确。因为传统计算流体力学软件等对双螺杆的模拟无法得出固体分布情况。对比这一情况，反映出利用DEM 方法分析双螺杆固体粒料的输送是可行的，也证明了DEM中内嵌的物理模型适用性较强，在参数设置得当的情况下，可以计算出接近双螺杆试验真实情况的结果。

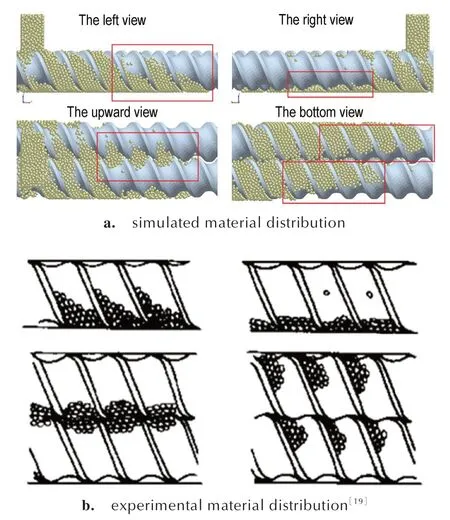
图5 固体颗粒物料在双螺杆中的分布Fig.5 Solid powder material distribution in the twin-screw extruder

（3）固体粒料在双螺杆中不同位置的填充率

通过总时长20 s 的计算，在螺杆的径向方向划分150 个统计网格单元组，统计每个网格中的粒子数目。结合螺杆的位置关系，统计了填充率随时间的变化关系，如图6a 所示。特别分析了16，17，18，19 s 的双螺杆的固体颗粒的填充情况，如图6b 所示。通过分析填充率分布图，可以发现，随着时间推移，啮合区填充率逐渐升高。在19 s 时，啮合区和螺杆末端反向螺纹元件位置处的物料填充率接近100%；在输送端位置处的物料填充率较低，大概为20%左右；而在啮合区后的螺纹输送区域的物料填充率较大，约为30%。随着时间的推移，螺杆前半部分螺纹输送端的物料填充率变化不大，而经过啮合段后的螺纹输送区域的物料填充率逐渐上升。这是由于在到达16 s 之前，前部分螺杆螺纹输送段的物料分布已经处于稳定状态；在时间达到19 s 后，螺杆啮合去后的螺纹输送段的物料填充率也逐渐达到了稳定状态。机筒各处填充率不同是由于不同的螺杆构型对颗粒的作用力不同。不同于螺杆螺纹输送段螺纹元件的摩擦拖拽，固体颗粒在啮合区的输送动力主要来源于啮合块的挤压。在啮合段的物料只有一个沿螺杆轴向的初速度，不存在直接向前运输的动力，受到啮合块的挤压作用，容易在啮合区处形成堆积。而反向螺纹元件位置处的物料颗粒速度受到螺杆作用改变运动方向，也会产生大量物料堆积。

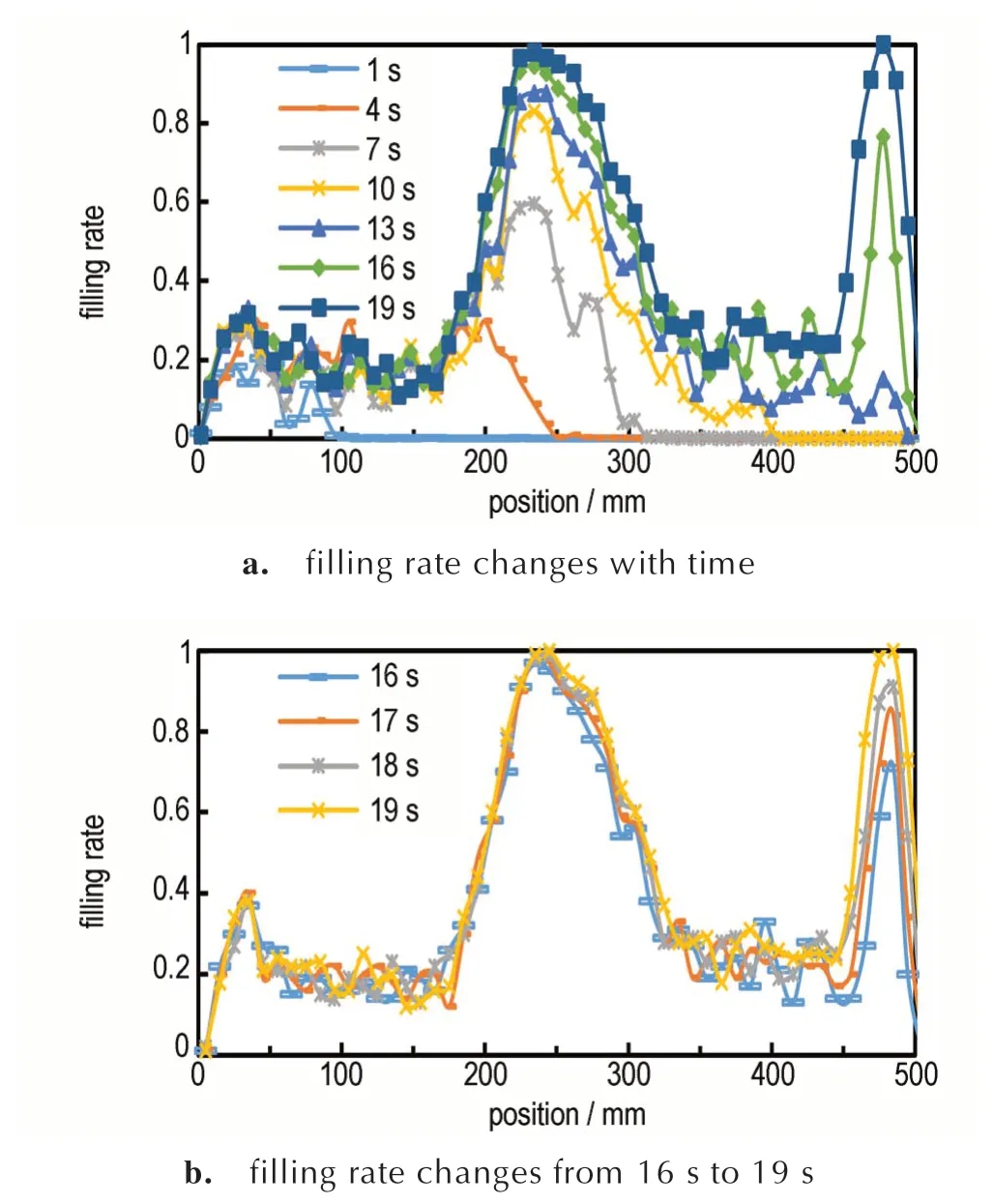
图6 沿双螺杆的物料填充率随时间变化情况Fig.6 Filling rate along the twin-screw at different time

5.2 DEM-CFD 耦合模拟结果分析

（1）填充率分布

经瞬态分析发现19 s 物料在螺杆中的输送已达到稳定状态，DEM-CFD 耦合模拟均采用19 s 时刻DEM 稳定状态的结果进行。图7 为DEM 法和DEM-CFD 耦合法模拟得到的固体颗粒在螺杆中的填充率分布曲线对比。在相同的工艺条件下，与DEM 得到的结果相比较，发现加入质量分数为15%的液相成分后，固体颗粒的分布填充情况大为改善，填充速率更快。前段螺纹元件输送段的填充率由20% 提升到40%，提升了将近一倍。结果反映液相的加入极大地改善了固体推进剂的流动性。啮合段的填充率接近为100%，加入液相后啮合段向下一段的输送能力明显得到了提高。

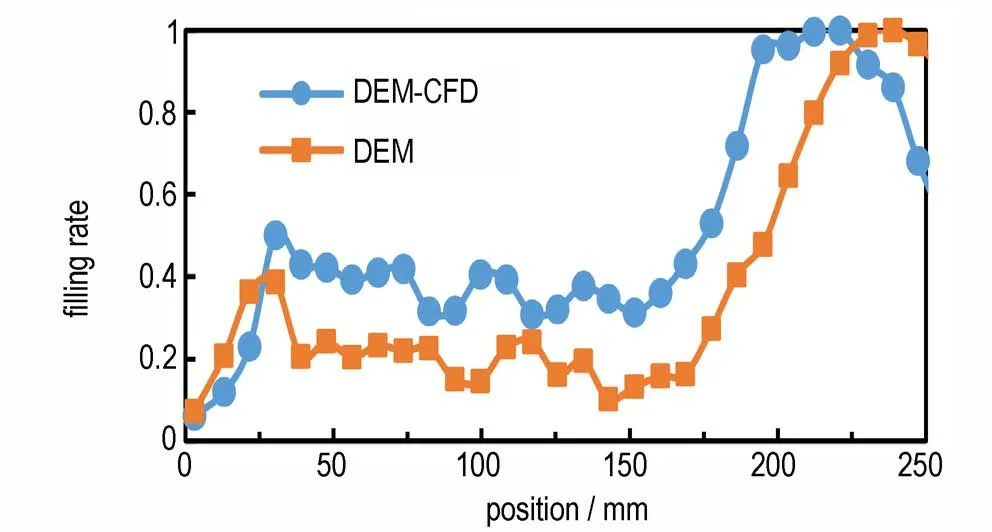
图7 沿螺杆方向的填充率分布图对比Fig.7 Comparison of filling rate distribution diagram in screw direction

（2）颗粒平均速度

图8a 为颗粒平均速度沿螺杆方向的分布曲线。加入液相的固体推进剂颗粒的平均速度远大于纯固体颗粒的平均速度。整体颗粒的平均速度由DEM 模拟得到的0.1 m·s-1提升到DEM-CFD 耦合得到的0.25 m·s-1。未加液相的固体推进剂颗粒与螺杆的摩擦主要为滑动摩擦，螺杆较难带动物料运输；颗粒的输送主要依靠螺杆的推力。而由液相包裹的颗粒形成浆体，有利于物料对螺杆的黏附，受到的螺杆剪切和摩擦力相对变大，利于物料的输送，运动速度也相对变大。而且，物料在啮合处受到啮合块的挤压作用，速度进一步上升。在进料口位置处，耦合计算时的物料平均速度突然上升，可能是由于进料量过大，在进料口大小不变的情况下，液体要达到设定进料速度必须有足够大入口速度。图8b 显示了颗粒最大速度沿螺杆方向的分布曲线。颗粒最大速度分布规律并不明显，耦合前后速度峰值变化不大，但是DEM-CFD 耦合计算得到的最大速度的平均值高于耦合前DEM 计算得到的最大速度平均值，说明液相的加入对颗粒最大速度的提高也有促进作用。

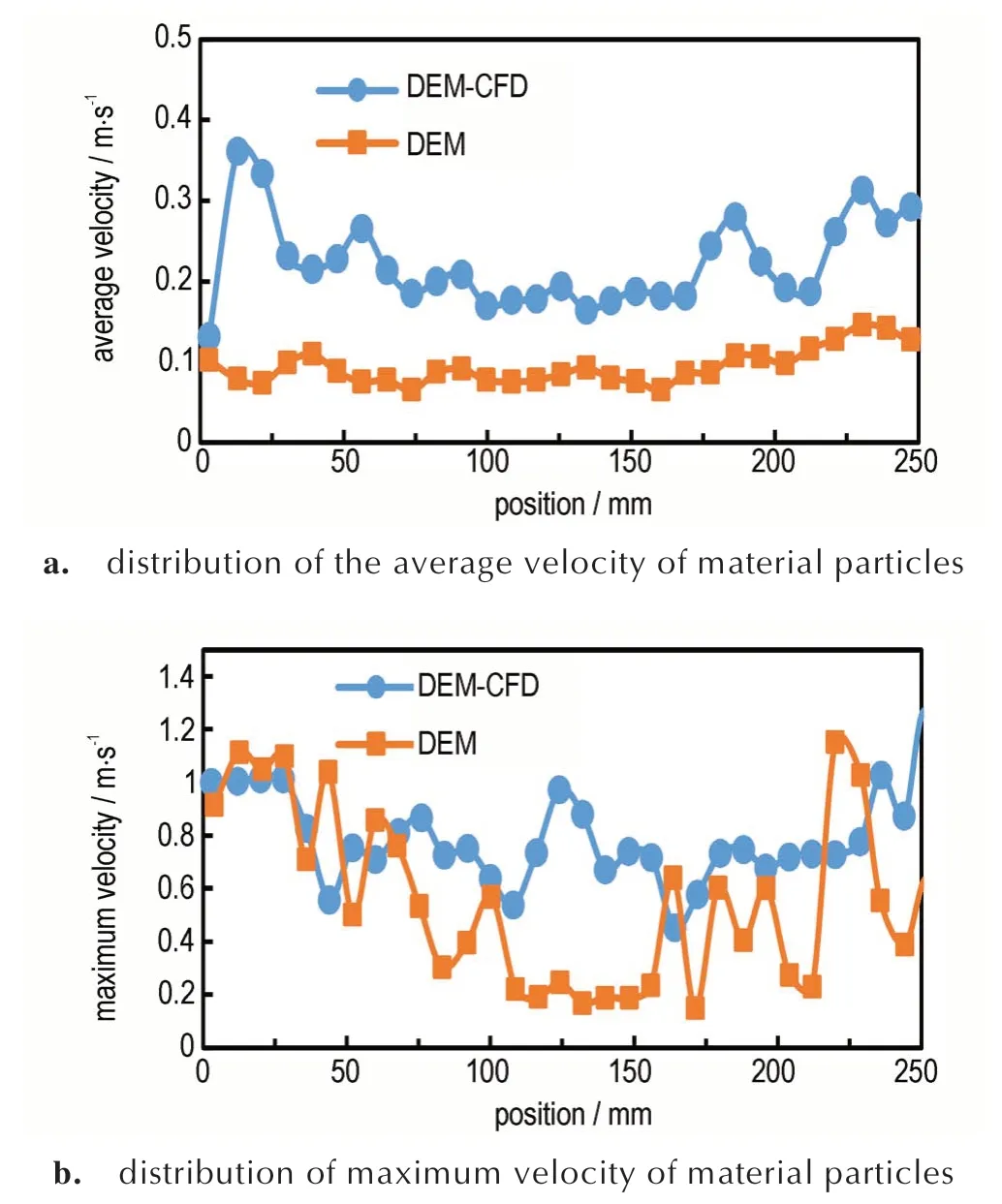
图8 沿螺杆方向的颗粒速度分布图Fig.8 Particle velocity distribution along the screw direction

（3）螺杆受力情况

图9 为DEM 和DEM-CFD 耦合计算得到的螺杆受力分布云图。图10 为DEM 和DEM-CFD 耦合计算得到的两根螺杆分别沿螺杆方向的受力曲线。两螺杆受力情况基本一致，最大受力点都出现于啮合区域及啮合块与螺纹元件连接位置处。加入液相前后螺杆受力变化不大。虽然液相的加入增加了物料的流动性，理论上能够降低螺杆的受力；但是较好的流动性也使得物料在螺杆中的填充率变大，物料堆积更多。因此，流动性的增强和物料的增多对螺杆产生的影响几乎相互抵消。

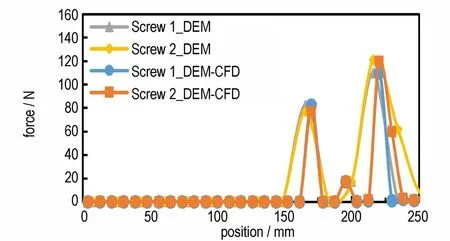
图10 沿螺杆方向的螺杆受力曲线Fig.10 Screw force curves along screw direction

6 结论

为了解决复合固体推进剂双螺杆挤出仿真中固液相性质差距较大的问题，首先通过DEM 方法对固体推进剂的主要固相颗粒物（铝粉和高氯酸铵）在双螺杆中的挤出过程进行了仿真分析，然后用DEM-CFD 耦合的方法对固液两相流的复合固体推进剂在双螺杆中的挤出过程进行了仿真分析，与DEM 计算得到的纯固体颗粒挤出过程进行对比，得到以下结论：

（1）对复合固体推进剂固相颗粒在双螺杆中挤出过程的DEM 模拟分析发现，DEM 法对于固体推进剂粉料的挤出混合过程得到的固体颗粒分布规律与双螺杆可视化实验结果相符，这是传统有限元分析方法难以实现的。考虑液相的加入，采用DEM 与CFD 相结合的耦合计算方法可实现更准确的模拟。

（2）DEM 模拟分析了不同喂料量条件下固相颗粒在螺杆中的分布情况，确定了螺杆转速70 r·min-1条件下最优的固体颗粒喂料量为75 kg·h-1。

（3）采用流变测试得到40 ℃时复合固体推进剂液相的黏度为1.78 Pa·s，该黏度值用于CFD 及DEM-CFD耦合仿真。在固体颗粒喂料量75 kg·h-1和转速70 r·min-1的工艺条件下，采用DEM-CFD 耦合模拟分析计算了固含量质量分数75%的复合固体推进剂在双螺杆挤出过程中的填充率、速度和螺杆受力情况。

（4）比对DEM 和DEM-CFD 耦合计算结果发现：加入液相物料后，颗粒平均速度由0.1 m·s-1提升到0.25 m·s-1；液相的加入增加了物料在输送段的填充率，由20%提升到40%，物料的输送效率也得到提升；螺杆的受力变化不大；在实际生产中应当着重注意啮合段螺杆及物料的受力情况。