单相LCL型并网逆变器的延时减小与补偿方法
邓淞元,赵 霞
(兰州交通大学 自动化与电气工程学院,兰州 730070)
随着电力电子器件的快速发展,分布式能源发电系统接入电网的规模日益增大,以电力电子技术为基础的分布式发电系统逐渐取代了传统的发电系统,成为电网中重要的一部分[1].并网逆变器作为分布式发电和电网之间能量转换的接口,在电网的安全、平稳和良好运行方面发挥着关键作用[2].
如今,由于数字控制强大的抗干扰能力、复杂的算法和多次编程的可实现性等,数字控制慢慢替换了电子领域的模拟控制,但是系统有源阻尼特性被延迟动作下的LCL并网逆变器改变了,致使并联在电容两侧的不再是纯电阻值,而是频率依赖性电阻,此电阻在频率大于fs/6(fs为采样频率)时会变成负阻.这种负阻特性会降低系统的鲁棒性,当谐振频率fr等于fs/6时,系统无法稳定[3].尤其是在弱电网下,电网阻抗的变化会致使滤波器谐振频率改变,可能会造成系统谐振频率等于fs/6[4],进而造成系统无法稳定.不仅如此,并网电流环产生的延时会导致环路带宽降低,使系统的动态性能下降.
文献[5-7]采用预测控制法对延时进行补偿,但是其需要准确的模型,由于在弱电网下,电网参数会发生变化,会使实际控制有较大误差,且无法补偿脉宽调制产生的延时.文献[8]提出了即时采样与零极点结合的方式补偿延时,但是其没有补偿并网电流环延时,导致系统相位裕度较低,动态性能较差.文献[9-10]采用超前补偿器来减小延时,但是超前补偿器会放大高频噪声,恶化并网电流品质.
本文首先分析了传统电容电流有源阻尼反馈控制的LCL单相并网逆变器,并建立了控制模型,分别分析了电容电流环和并网电流环对系统的影响;之后,针对存在的问题,提出了一种基于双电流闭环的即时采样与零极点结合的方式对系统的鲁棒性和动态性能进行改善.
1 传统电容电流有源阻尼反馈
1.1 LCL单相并网逆变器模型
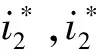

图1 LCL单相并网逆变器模型
Gc(s)=e-sTs.
(1)
脉冲宽度调制延迟特性类似于零阶保持器(ZOH),零阶保持器的s域函数为
Gh(s)=(1-e-sTs)/s≈Tse-0.5sTs,
(2)
其中,Ts是数字控制时的采样周期.所以脉宽调制引入了半个采样周期的延时,此时系统总延时传递函数
Gd(s)=Gc(s)Gh(s)=Tse-1.5sTs.
(3)
考虑延时后得到的LCL并网逆变器的数学模型如图2所示,其中1/Ts代表采样开关环节在连续域中的传递函数[11].由逆变器模型可以得到系统在连续域下的传递函数为
Td(s)=(Hi2KPWMe-1.5sTsGi(s))/(s3L1(L2+Lg)C+s2(L2+Lg)CHi1KPWMe-1.5sTs+s(L1+L2+Lg)),
(4)
其中:调制波vm经计算延迟后得到vm1;vm1经零阶保持器后的信号到逆变桥输出电压vinv的传递函数为KPWM=Vin/Vtri(Vin为输入电压,Vtri为三角载波幅值).
从式(4)中可以看出,分子分母均存在延时环节,其中:分子的并网电流反馈延时会降低系统的稳定裕度和动态响应;分母会影响电容电流反馈有源阻尼特性[12].
1.2 延时环境下LCL并网逆变器鲁棒性
对图2控制框图进行等效变换,得到图3.从图3中可以看出,在系统环路中,电容两侧并联了一个阻抗,其表示式为

图2 LCL并网逆变器数学模型

图3 变换后的控制框图
Zeq=L1Ts/(KPWMHi1CGd(s))=RAe1.5sTs,
(5)
其中,RA是非延时环境下电容电流反馈有源阻尼的等效电阻.
根据式(5),Zeq可表示为电阻Req与电抗Xeq并联,如图4所示.

图4 等效虚拟阻抗
将s=jw代入式(5)后可得:
Req(w)=RA/cos(1.5wTs),
(6)
Xeq=RA/sin(1.5wTs).
(7)
根据式(6)和式(7)画出Req和Xeq的频率特性,如图5所示.从图5中可以看出:Req在fs/6处会变成负阻状态;Xeq在fs/3时会从感性变成容性.由于Req的负阻特性,当fr大于fs/6时(此时只讨论Hi1>0),由于弱电网下电网阻抗增大时会使谐振频率左移,可能会导致fr=fs/6,此时系统无法满足奈奎斯特定理,造成系统无法稳定,所以要减小其延时来增强系统鲁棒性.

图5 Req和Xeq的幅频特性
1.3 并网电流环延时对系统的影响
在同步采样下,并网电流环存在一个采样周期的延时[13].不同采样方式下,系统的延时不一样,为了便于阐述,引入延时系数λ1(0≤λ1≤1)和λ2(0≤λ2≤1).假设电容电流环的计算延时为
Gc1(s)=e-sλ1Ts.
(8)
并网电流环的计算延时为
Gc2(s)=e-sλ2Ts.
(9)
根据式(8)和式(9),可以将式(4)变化为式(10).
Td1(s)=(Hi2KPWMe-s(λ2+0.5)TsGi(s))/(s3L1(L2+Lg)C+s2(L2+Lg)CHi1KPWMe-s(λ1+0.5)Ts+s(L1+L2+Lg)).
(10)
假设有源阻尼环的延时λ1=1(同步采样下),画出λ2取不同值时式(10)的bode图,如图6所示.从图6中可以看出:补偿并网电流环延时对系统幅频特性几乎没有影响;但是随着并网电流环延时的不断减小,系统的相位裕度不断提高,动态性能变好.
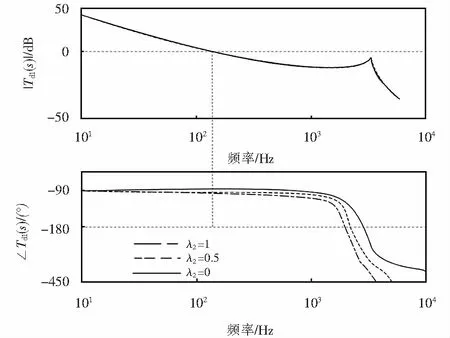
图6 并网电流环延时λ2取不同值时Td1的bode图
2 双电流闭环即时采样与零极点补偿结合控制策略
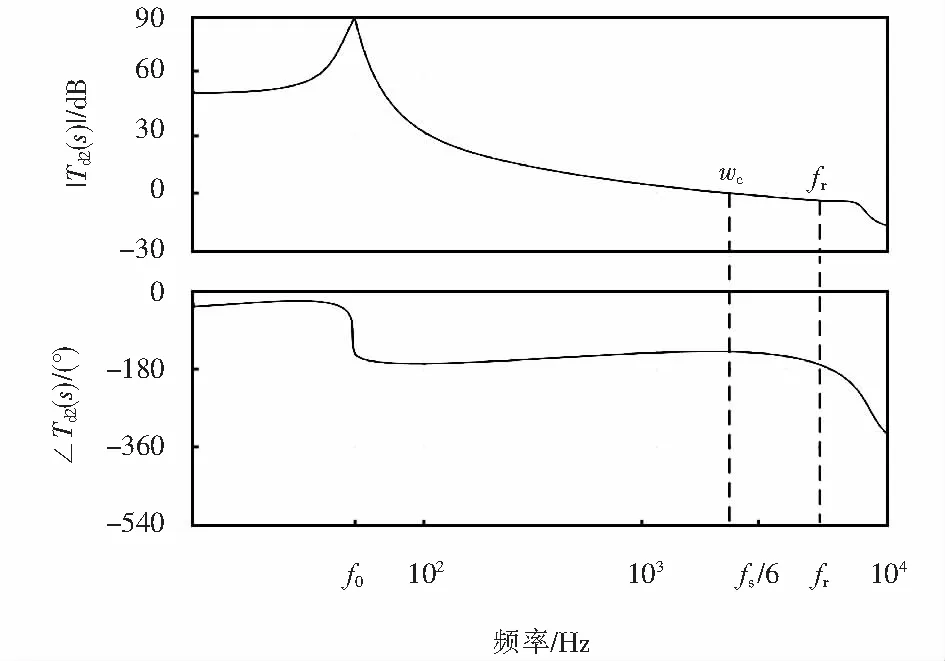
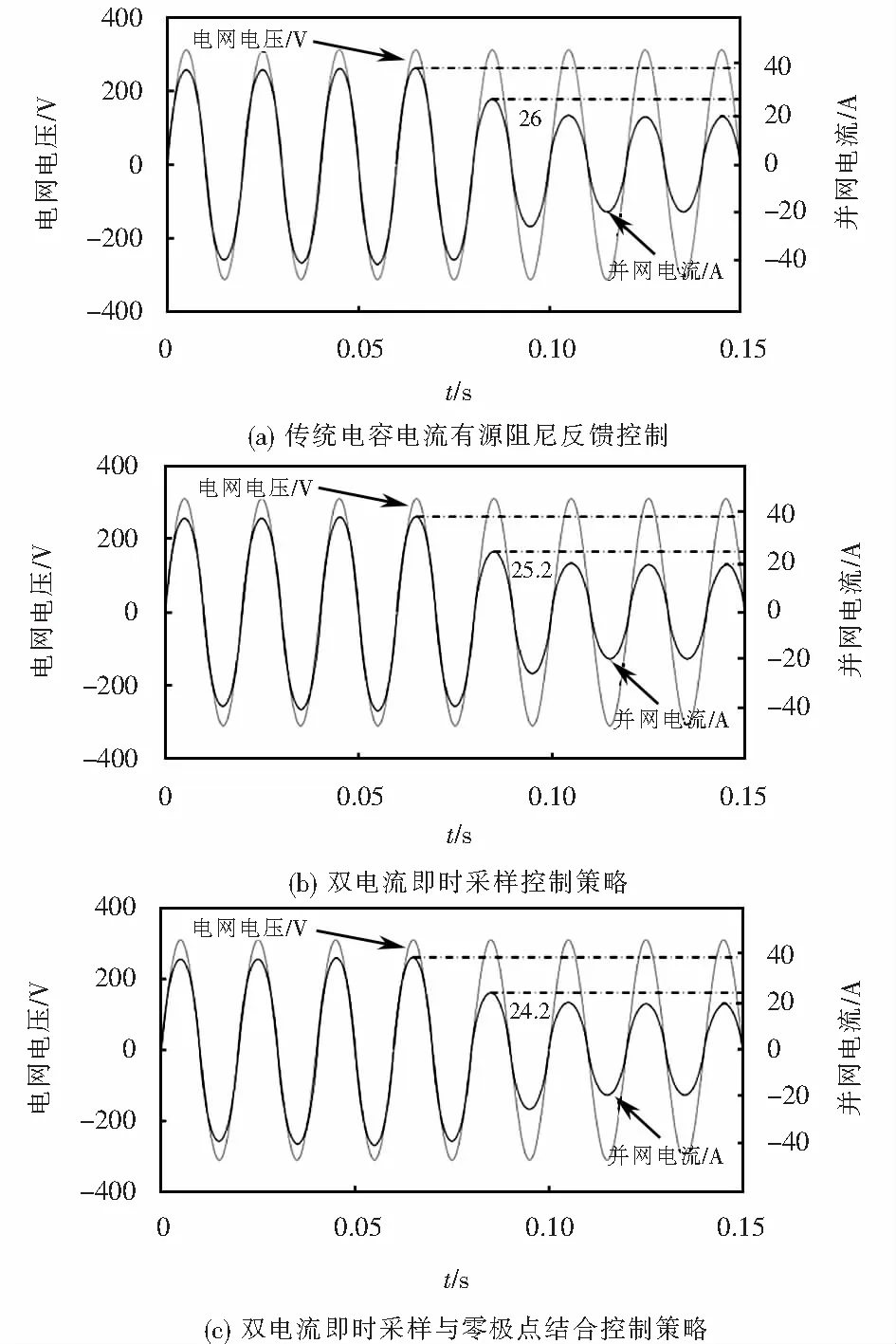
为了避免开关纹波和高频的开关噪声,通常是在一个采样周期进行两次采样(即三角载波的波峰和波谷处),此时称为同步采样.同步采样会产生一个周期的计算延时,如图7所示,电容电流ic和并网电流i2在第k拍进行采样后经过一个周期的计算延时,在第k+1拍更新了调制波vm.如果不在波峰和波谷处进行采样,而是将电容电流采样时刻提前Td1,将并网电流采样时刻提前Td2,由于Td1、Td2< 图7 数字控制采样与装载过程 从文献[12]可以得到经过电容电流即时采样后的Req1(w)和Xeq1(w)的幅值特性,如图8所示. 由图8可以看出:Req1(w)在fs/2(奈奎斯特频率)以内是正阻,Xeq1(w)是感抗;当fr大于fs/6,Req1在fr处为正阻,此时消除了开环增益的两个右半面极点,系统相频曲线只在fr处穿越-180°,即使电网阻抗变化使fr=fs,只需要fr处的幅值裕度大于0 dB,系统就可以稳定,提高了系统对弱电网的适应性. 图8 采样后的Req1和Xeq1的幅值特性 由上述分析可知:并网电流环存在的延时会导致系统稳定裕度下降;由于并网电流不存在开关纹波,所以可以将该采样方法应用于并网电流环中[14],消除并网电流环的计算延时,提高系统的动态性能. 除了上述的并网电流环计算延时和电容电流环计算延时外,还有脉宽调制控制中的半个采样延时.针对此延时,文献[15]提出在系统前向通路中加入零极点补偿器来补偿脉宽调制延时.零极点补偿器的传递函数如式(11)所示.根据文献[15],零阶保持器的传递函数可以写为式(12). C(z)=2z/(z+1), (11) C0(s)=(1-e-sTs)/s≈Ts/(1+sTs/2). (12) 对式(12)进行离散化处理,如式(13)所示. Ts/(1+sTs/2)=(Ts/2)×(z+1)/z=C0(z). (13) 在控制环路中加入零极点补偿环节,可得C(z)C0(z)=Ts,这样消除了脉宽调制延时[13].由此画出系统总的控制框图,如图9所示.从图9中可以看出:并网电流环和电容电流环均没有了计算延时,且零极点补偿了脉宽调制延时.此时可以得到系统在连续域下的传递函数为 图9 变换后的控制框图 Td2(s)=Hi2C(s)Gi(s)e-0.5sTs/(s3L1(L2+Lg)C+s2(L2+Lg)CHi1C(s)KPWMe-0.5sTs+s(L1+L2+Lg)). (14) 根据式(14)可以得到系统的开环增益bode图,如图10所示. 图10 采用本文所提控制方法的bode图 φ(wc)为系统在wc处的相位,A(fr)是系统在fr处的幅值.系统相位裕度计算式为φ(wc)-(-180°),可以得到系统相位裕度为48.3°;且fr处的幅值裕度计算式为0-A(fr),可以看出幅值裕度显然大于0;所以此时系统是稳定的,且相位裕度较高. 图11表示电网阻抗变化时采用本文控制方法所得开环极点分布图.箭头方向代表电网阻抗逐渐增大. 由图11可以看出:当Ls≥248μH时,即fr≥fs/6时,系统的极点一直在z域的单位圆内,满足系统稳定的要求;因此采用本控制策略时,鲁棒性较好.综上所述,本系统控制策略在提高系统鲁棒性的同时提高了系统稳定裕度. 图11 系统开环极点分布图 为验证本文所提方法的有效性,通过Matlab/Simulink仿真软件搭建图1所示的LCL并网逆变器模型,仿真参数如表1所列. 表1 系统参数 当Lg=248μH,fr=fs/6=3.3kHz,并网电流波形如图12(a)所示,可以看出,传统电容电流反馈控制并网电流存在明显的震荡现象.图12(b)和图12(c)分别是双电流即时采样、双电流即时采样与零极点结合控制策略下的并网电流波形,可以看出:两种控制方式均能使系统处于稳定状态,提高了系统的鲁棒性. 图12 并网电流仿真波形 为了验证系统的动态性能,将上述的三种控制方式分别进行了跳变试验.图13(a)为传统电容电流有源阻尼控制下的并网电流从半载跳到满载时的动态波形,图13(b)是双电流即时采样的跳变试验波形,图13(c)是双电流即时采样与零极点结合的跳变试验波形.经测得上述三种控制方式的超调量由分别是35%、26%和21%,可见,加入零极点补偿后的系统超调量更低,动态性能更好. 图13 并网电流的跳变试验波形 对于数字控制下的LCL并网逆变器系统的延时问题,本文提出了基于双闭环即时采样和零极点结合的控制策略,不仅减小了电容电流环和并网电流环的延时,还补偿了脉宽调制延时,增强了系统的鲁棒性和动态性能,最后在Matlab/Simulink仿真软件上验证了所提方法的有效性.相对于之前学者提出的双电流即时采样控制策略,本文又增加了零极点补偿措施,对脉宽调制延时进行了补偿,使系统具有更好的动态性能.除此之外,锁相环对于系统的稳定性有一定影响,本文对此没有进行研究,可以针对锁相环对延时环境下系统稳定性的影响进行进一步研究.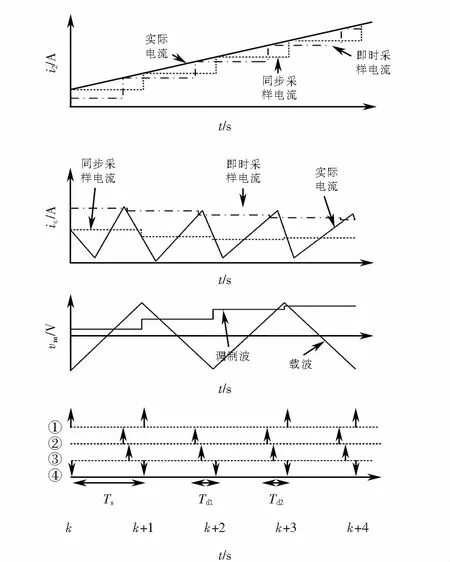


3 仿真验证


4 结论

