基于CMA模式体系的京津冀地区复杂地形下冬季的精细化地面要素多模式集成预报研究*

佟 华 张玉涛 齐倩倩 王远哲 王大鹏

1 中国气象局地球系统数值预报中心，北京 100081 2 灾害天气国家重点实验室，北京 100081

提 要： 基于CMA模式体系的四个模式(CMA-GFS、CMA-REPS、CMA-MESO 3 km、CMA-MESO 1 km)和2020年12月1日至2021年3月15日的近地面要素2 m温度、10 m风速、2 m相对湿度预报，对京津冀地区复杂地形下冬季误差订正后的各要素进行基于贝叶斯模型平均(BMA)方法的多模式集成试验。结果表明，每个模式各要素误差订正后的均方根误差都有明显的减小。BMA方法多模式集成后预报效果优于每一个参加模式，2 m温度BMA预报较几个模式原始误差的改进在0.5～1.4℃，均方根误差减少了20%～40%，10 m风速和2 m相对湿度的均方根误差分别减少了12%～45%和25%～35%。各要素均方根误差水平分布表明不同要素在不同地形高度的地区误差分布明显不同，此方法使得京津冀地区的误差显著减小。此外，BMA预报的概率分布情况可定量地预测各要素的不确定性。

引 言

随着数值预报技术不断进步，准确率不断提高，数值预报结果已经成为预报员的重要参考。而来自不同研发单位、不同分辨率、不同预报特点的海量数值预报产品对预报员的高效使用产生了较大挑战，迫切需要对多种预报特色的预报产品基于检验进行多模式统计后处理集成，从而获得效果更优的预报结果。在多模式集成技术中，贝叶斯模式平均(Bayesian model averaging，BMA)方法是一种非常有效的提高模式预报准确率的方法(Raftery et al，2005；代刊等，2018)，此方法将观测与不同模式得出的预报结果作为先验信息，通过求解参数，计算各模式相对最优的权重等参考值，此权重就是预报变量后验概率分布，代表着每个模型在训练阶段相对的预报技巧。再经过对偏差校正后的单个模型概率密度函数(probability density function，PDF)加权平均，得到多模式成员预报的连续的PDF，它不偏好也不摒弃各个模型，而是对各个模型结果进行综合，融合更多信息，以发挥各模型优势，因此其预测均方根误差通常小于单个预测的误差。自从Raftery et al(2005)、Gneiting and Raftery(2005)指出BMA方法对天气预测非常有效后， BMA方法在气温、风速、降水、能见度等天气和气候预测中得到广泛应用。刘建国等(2013)基于TIGGE多模式集合预报资料进行24 h气温的概率预报，极大地提高了地面气温的预报技巧。智协飞等(2018)基于BMA方法对地面气温延伸期概率预报，提高了延伸期温度预报技巧，进一步展示出超级集合产品进行BMA概率预报的应用潜力。陈朝平等(2010)、韩焱红等(2013)利用BMA方法对区域和全球集合预报模式的降水概率预报产品进行修正，更新的概率分布有效增强了暴雨可能出现的信号。祁海霞等(2020)基于降水集合预报资料，对清江流域的降水预报进行试验分析，BMA模型预报比原始集合预报有更高预报技巧。Sloughter et al(2010；2013)的研究表明BMA订正方法能够明显地改善北美洲西北部地区的最大风速和风向的预报。石岚等(2017)利用BMA模型对ECMWF集合风速预报产品进行预报校准，减小了风速预报误差，MAE降低了11.7%。Chmielecki and Raftery(2011)对能见度要素进行BMA概率预报研究，改善了原始集合模式能见度预报的概率密度函数。

中国新一代数值天气预报系统GRAPES(Global and Regional Assimilation and PrEdiction System-Mesoscales Ensemble Prediction System)是中国气象局自主研究并初步建立的多尺度通用资料同化与数值天气预报系统，建成了从区域3～10 km 到全球25～50 km分辨率的确定性与集合预报的完整数值天气预报业务技术体系(沈学顺等，2020；薛纪善和陈德辉，2008)，现统一更名为CMA模式。2020年CMA数值预报业务体系主要包括CMA-GFS全球中期预报系统(Zhang et al，2019；Chen et al，2020)、CMA-MESO区域高分辨率预报系统(黄丽萍等，2017)、CMA-GEPS全球集合预报系统(李晓莉等，2019)、CMA-REPS区域集合预报系统(陈静和李晓莉，2020；张涵斌等，2014)、CMA-TYM区域台风预报系统(麻素红和陈德辉，2018)等，为气象预报服务和防灾减灾提供重要的支撑作用。为更好地提供气象保障服务，发挥CMA各模式的优点及整个模式体系的综合效益，需要对CMA体系产品进行误差订正及多模式集成技术进行模式融合，得到集成预报产品，为预报员提供更准确的天气预报服务。

2022年北京冬奥会首次在冬季季风性大陆气候地区举行，大部分户外雪上赛事在地形复杂的延庆赛区和张家口赛区举行，气象条件在不同地点的差异非常大，而且赛事对气象要素的要求也非常严格，因此对京津冀高精细化次公里分辨率的近地面气象要素预报，而以往对北方冬季复杂地形下近地面气象要素的精细化预报研究较少。另一方面，之前的集成研究主要针对ECMWF集合预报产品以及TIGGE超级集合产品，对同一个模式体系不同分辨率模式进行集成以提高模式体系的预报技巧的研究还不多见。本文旨在针对CMA模式体系不同分辨率模式对不同要素预报技巧存在差异并各有优势的特点，对CMA不同分辨率模式进行集成，以获得复杂地形下更准确的近地面要素预报及其概率特点，为北京冬奥会气象预报服务提供更精细化更有准确的要素预报产品。

1 多模式集成方法介绍

本文中采用首先对CMA体系中的每一个模式分别进行误差订正去除系统误差，然后再进行多模式集成的方法，得到各近地面要素的集成预报结果。

1.1 误差订正方法介绍

采用一阶自适应的卡尔曼滤波方法，这是一种基于卡尔曼滤波思想，通过不断对模式误差进行更新，获得当前时刻的误差估计值，来降低偏差尺度的方法(Cui et al, 2012；佟华等，2014)。这种方法既考虑了气候平均预报误差特征，保证了估计误差整体的稳定性，又加入了临近时刻误差信息，融入了天气系统连续性特点，将二者以权重系数相结合，共同估计递减平均误差。公式如下：

Bi(t)=(1-ω)Bi(t-1)+

ω[fi(t-1)-Oi(t-1)]

(1)

Fi(t)=fi(t)-Bi(t)

(2)

式中：t代表当前预报时间，i代表各站点，fi和Oi分别代表各站点的预报值和对应时间的观测值，Bi(t)定义为当前预报时间经过权重平均后的模式预报偏差估算值，通过权重系数ω的选择，对两个不同时段(前一天和历史累积)的模式预报偏差加权平均而获得。对于权重系数，本文选用0.05，该系数是根据中国气象局2017年参加ICE-POP 2018冬季试验时做的敏感性试验确定的(张玉涛等，2020)。利用系统平均加权误差Bi(t)对预报值fi(t)进行误差订正，得到各站点当前预报时间订正后的预报值Fi(t)。

1.2 BMA多模式集成方法介绍

BMA是一种结合多个模型进行联合推断和预测的统计后处理方法，是多个模型后验分布的加权平均(Raftery et al,2005)。令f=f1,…,fK，分别假定f是K个不同数值模式的预报结果，y代表需要预报的变量，YT代表训练数据。BMA预报的概率密度函数PDF可表示为如下的多模式预报加权平均的形式：

(3)

y|(fk,YT)～gk(ak+bkfk，σ2)

(4)

对于风的预报，由于风速的概率密度分布大多呈现偏态的特点，很多研究使用Gamma分布作为风速的分布函数(Sloughter et al，2010；Eide et al,2017)，也有研究采用截断正态分布(Frogneret al，2016；石岚等，2017)。本研究对于研究区域大量的观测分布显示，风场和湿度场可近似满足截断正态分布，为了方便各个要素统一处理，假定地面风和相对湿度服从截断正态分布，其中风速：g(x|μ,σ)=0,x<0；相对湿度：g(x|μ,σ)=0,x<0 或x>100。

由式(4)和式(3)可知BMA预报均值，即BMA模型多模式集成的确定性预报结果表示为：

(5)

然后使用训练数据，利用EM算法(expectation maximization algorithm)进行极大似然估计，通过极大似然原则求解对数似然函数来求解BMA预报模型参数wk(k=1,2,…,K)：

L(w1,…,wk,σ2)=

(6)

假设预报误差在空间s与时间t上相互独立，上述方程由于不存在解析的极大值解，参数wk(k=1,2,…,K)与σ2需要进行迭代求解获得。

BMA方法进行多模式集成预报主要包括以下几个步骤：(1)确定训练期长度；(2)对训练期数据采用EM算法进行模型参数率定，获得相应的BMA模型；(3)设计训练期为一个滑动窗口进行滚动预报，即BMA采用先前的N天作为训练期进行训练，训练出的BMA系数应用到下一天的BMA模型预报中，从而每一天动态建立研究区域内各点的BMA模型。

2 研究区域和资料

将试验区域定为东西方向约700 km、南北方向约680 km的京津冀地区范围，分辨率为0.01°×0.01°。图1为试验区域的地形高度，整个区域呈现西北地形高、东部和南部地形低的特点。西北部山区地形高度都在1000 m以上，东南部平原则基本在100 m以下。采用CMA模式体系的CMA-GFS、CMA-REPS、CMA-MESO 3 km、CMA-MESO 1 km模式系统进行多模式集成试验，试验要素包含2 m温度和相对湿度、10 m风。其中CMA-MESO 1 km 模式是面向精细化预报需求，基于CMA-MESO 3 km 高分辨率快速循环同化预报业务系统，通过提高模式动力框架计算精度和稳定性，引进更为精细的下垫面资料，选择合适的物理过程参数化方案组合等，所建立的覆盖京津冀的重点区域1 km分辨率的CMA-MESO高分辨率数值预报系统。首先对四个模式分别进行空间和时间降尺度，空间降尺度采用双线性插值，时间降尺度采用线性插值,形成京津冀地区1 km分辨率和每小时间隔的统一的格点预报场。再基于国家气象信息中心1 km分辨率多源气象数据融合格点实况产品进行误差订正。这个格点实况产品是利用数据融合和数据同化技术，综合地面自动气象站、雷达、卫星等多种来源观测资料及多模式模拟数据，获得的高精度、高质量、时空连续的多源数据融合气象格点产品(师春香等，2018；2019)。采用一阶自适应的卡尔曼滤波方法，分别得到四个模式误差订正后的预报结果。其中CMA-REPS区域集合预报模式的误差订正采用对控制预报进行卡尔曼滤波得到误差文件，再应用到每个成员进行订正的方法。然后使用BMA方法进行四个模式的集成，根据选取的训练期，计算每个模式的权重系数w和方差，每天动态建立BMA模型。使用各模式00时(世界时，下同)起报的0～24 h预报，从2020年12月1日开始进行订正和集成试验，对2021年2月1日至3月15日进行预报并检验其预报效果。

图1 模拟区域地形海拔高度Fig.1 Terrain height in simulated domain

3 预报试验结果分析

3.1 训练期长度确定

使用BMA方法进行多模式集成，不同的训练期长度会对集成结果产生影响，因此需要对BMA方法的训练期长度确定进行试验。表1分别是训练期为20、25、30 、35、40 d的2 m温度、10 m风速和2 m相对湿度24 h平均的均方根误差比较，综合对比各要素各时效不同训练期的误差情况可见，训练期为30 d时综合误差最小，因此使用此训练期长度进行后续的分析和评估。

表1 不同训练期均方根误差比较Table 1 Comparison of RMSE in different training periods

3.2 多模式集成预报试验及检验结果分析

对2021年2月1日至3月15日00时起报的24 h内的逐小时多模式集成预报进行评估检验。图2分别为CMA-GFS、CMA-REPS、CMA-MESO 3 km、CMA-MESO 1 km四个模式2 m温度(图2a)、10 m风速(图2b)和2 m相对湿度(图2c)在原始、订正后和BMA集成的0～24 h预报均方根误差格点平均。由图可见，三个要素各个预报时效误差订正后都较模式原始预报有明显改进，而模式集成后的误差在各个时效都明显优于每个模式的订正结果。

图2 各模式不同预报时效的(a)2 m温度，(b)10 m风速，(c)2 m相对湿度预报的原始、订正后和集成后均方根误差对比Fig.2 The root-mean-square error (RMSE) comparison of the original, corrected and blended forecast about (a) 2 m temperature, (b) 10 m wind speed, (c) 2 m relative humidity of each model in 0-24 h lead time

2 m温度方面，四个模式的原始误差、订正和集成后的误差都呈随着预报时效的增加逐渐增大的趋势。对于不同时效，订正后的温度预报误差较订正前有明显减小，均方根误差减小在0.2～1.0℃。四个模式总体效果比较来看，CMA-MESO 1 km温度的原始预报与订正后的预报效果优于其他三个模式，其中原始误差较其他模式的优势在0.5℃左右，订正后优势为0.2℃，可见原始误差越大的订正效果越明显。多模式集成后虽然仍像原始结果一样存在一定日变化，总体均方根误差在1.8～2.2℃，较订正后预报误差最小的模式又有0.3℃的改善，较几个模式原始误差的改善在0.5～1.4℃，误差改善率为20%～40%。

10 m风速方面，总体看四个模式的预报效果相差明显，尤其在9 h时效以后。区域格点平均的均方根误差从小到大分别是CMA-GFS、CMA-MESO 1 km、CMA-MESO 3 km、CMA-REPS，而且误差小的模式原始误差甚至优于误差稍大的模式的订正后误差。各个模式中，CMA-GFS的风速误差最小且优势明显，原始误差在2 m·s-1左右，订正后误差约为1.8 m·s-1，并且不同时效的预报误差很稳定，并没有其他三个模式误差随时效延长而增长的趋势。这些都和在日常的风速预报中全球模式如ECMWF、CMA-GFS和NCEP_GFS模式误差稳定小于区域模式的情况相符,分析原因认为全球模式对于大的形势场预报较区域模式更稳定。四个模式集成后,结果仍略优于CMA-GFS订正结果，均方根误差在1.75 m·s-1左右，并且预报误差稳定，随预报时效的增加误差增大不明显。BMA 集成后较几个模式原始误差的改善在0.3～1.4 m·s-1，误差改善率约为12%～45%。

2 m相对湿度的订正和集成效果非常明显，每个模式经过订正后均方根误差都减小了4%左右，多模式集成之后误差又减小了1%～4%。四个模式随着预报时效的增加均方根误差表现有所不同，其中CMA-REPS、CMA-MESO 3 km、CMA-MESO 1 km的原始误差非常接近，订正后的误差结果也非常相似，都是在1～6 h时效误差有所下降，之后开始逐渐上升,订正后的误差从10%左右增加到24 h预报的15%。而CMA-GFS的误差随时效的变化明显与其他三个模式不同，其在9 h时效之前的误差是稳定上升的趋势，均方根误差比其他三个模式大3%左右，而9 h时效后误差开始逐渐下降，总体误差在12%～14%，到15 h时效后均方根误差开始比其他三个模式更低。多模式集成预报同样随着时效增加误差改善得越明显，最终误差在9%～12%，改善率为25%～35%。

3.3 各模式权重对比

图3分别为相应的四个模式各时效2 m温度(图3a)、10 m风速(图3b)、2 m相对湿度(图3c)的集成权重系数对比，由图可见，各要素各时效的集成权重是根据模式的预报效果动态改变的。如图3b的10 m风速预报中，CMA-GFS模式的风速误差明显小于其他三个模式，它的权重系数达到0.4～0.55。CMA-MESO 1 km预报误差位列次席，且随着时效增加误差稳定并有减小的趋势，与CMA-GFS的误差逐渐接近，因此在9 h时效以后权重占比明显增加，达到0.3～0.4。CMA-MESO 3 km和CMA-REPS因误差相对最大，权重系数很小，为 0.1 左右。对于2 m相对湿度(图3c)，各模式的集成权重系数与模式预报误差的变化趋势非常一致，在预报前期CMA-GFS误差相对较大的时效，集成权重系数相对最小，随着后期预报误差减小，权重系数也迅速增加，到24 h预报时达到了0.4，其他三个模式则逐渐下降到0.25左右。2 m温度(图3a)的权重系数也基本符合上述规律，可见BMA多模式集成方法能够根据训练期各模式的预报效果动态调整各模式所占的权重，从而得到比所有模式预报效果更优的确定性预报结果。

图3 各模式不同预报时效的(a)2 m温度，(b)10 m风速，(c)2 m相对湿度预报权重系数对比Fig.3 The weight coefficient comparison of each model about (a) 2 m temperature, (b) 10 m wind speed, (c) 2 m relative humidity in 0-24 h lead time

图4为2021年2月1日至3月15日平均CMA-MESO 1 km原始模式(图4a,4c,4e)及多模式集成预报(图4b,4d,4f)的京津冀地区2 m温度(图4a,4b)、10 m风速(图4c,4d)和2 m相对湿度(图4e,4f)24 h预报均方根误差水平分布。总体来说整个地区的误差都有明显减小，但不同要素在不同地形高度的地区误差分布明显不同。温度误差较大的地区分布在北京城区西北向地形较高的山区，原始误差可达到4℃，其他平原地区误差在2℃左右，多模式集成后北京西部和北部山区的误差减小到2～3℃，城区及以南地区则减小到1～2℃。10 m风速和2 m相对湿度的误差分布与温度分布正相反，误差相对较大的地区分布在城区及以南地区，其原始CMA-MESO 1 km和集成后山区风速误差从非常不均匀的0～5 m·s-1下降到0～1 m·s-1；而在北京城区及以南的平原地区，风速误差从2～5 m·s-1下降到1.5～2.5 m·s-1。相对湿度误差从20%～30%降到10%左右，且在进行集成后山区和平原地区的误差分布非常均匀，基本不存在地形方面的差异了。综上分析，多模式集成后三个要素误差较大的地区预报效果都有明显减小，订正和集成的技术方案和效果都是较为理想的。

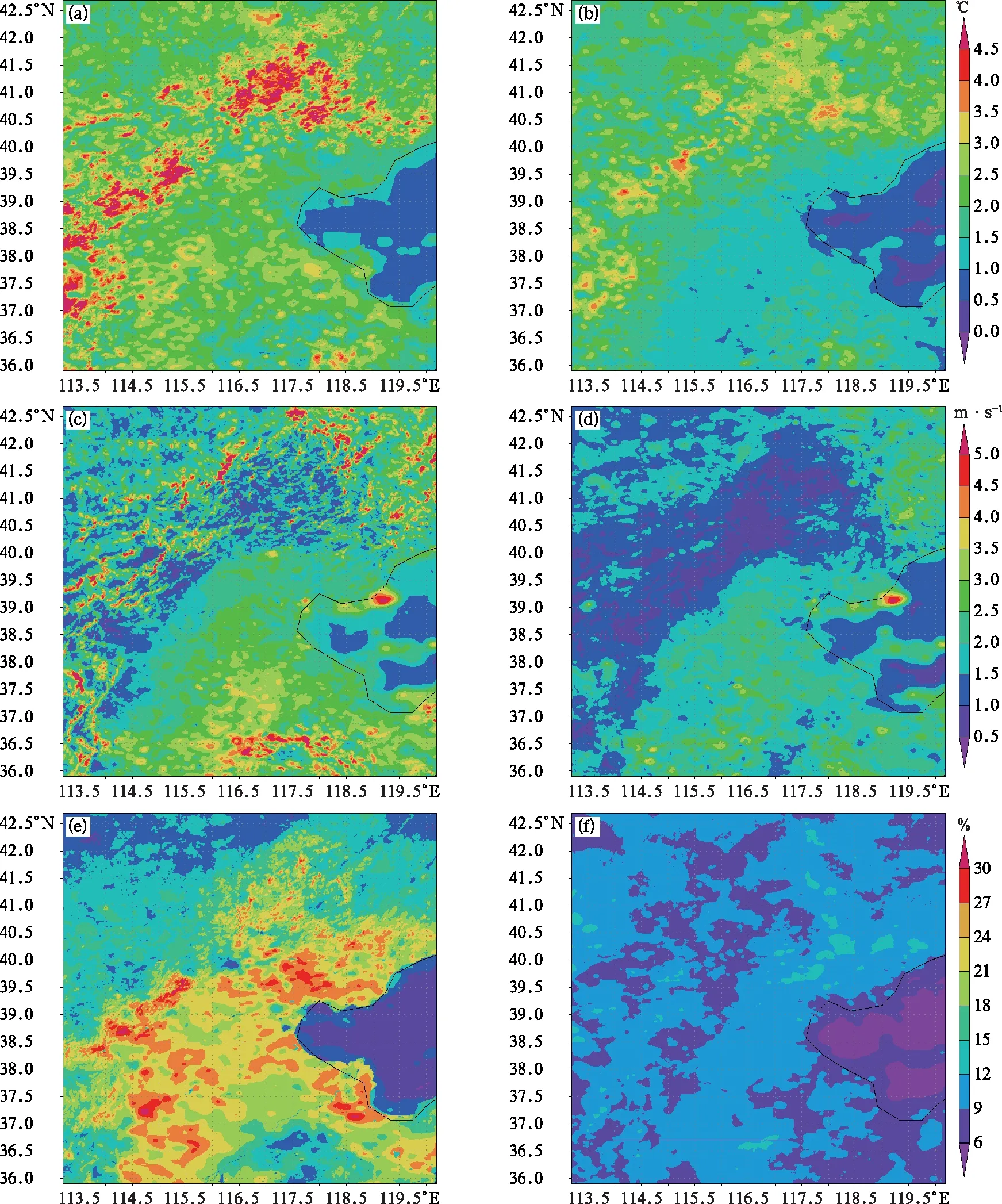
图4 2021年2月1日至3月15日平均(a,c,e)CMA-MESO 1 km原始模式与(b,d,f)多模式集成预报的京津冀地区(a,b)2 m温度，(c,d)10 m风速，(e,f)2 m相对湿度24 h预报均方根误差分布Fig.4 Comparison of the 24 h forecast RMSE distribution of (a, b) 2 m temperature， (c, d) 10 m wind speed， (e, f) 2 m relative humidity between (a, c, e) the original CMA-MESO 1 km and (b, d, f) multi-model blending forcast averaged from 1 Febuary to 15 March 2021

3.4 个例分析

3.4.1 确定性预报分析

对2021年3月9日00时起报24 h预报进行了个例分析。考虑到统计后处理主要的优势在于对较稳定存在的系统误差进行修正，因此没有选择较为极端的天气个例，而选择了较为普通的一天：3月9日为个例。图5为3月9日00时起报24 h预报的2 m温度(图5a～5d)、10 m风速(图5e～5h)、2 m 相对湿度(图5i～5l)的水平分布对比，其中每行从左至右，分别为观测、CMA-MESO 1 km模式原始预报、CMA-MESO 1 km订正结果、多模式集成结果。由图可见，经过误差订正的模式预报，都较原始预报更接近观测实况。而再经过多模式集成后，则较误差订正后的预报更进一步接近观测实况。如2 m 温度预报，原始预报在京津冀地区北部地形较高的山区和在北京城区及以南的平原地区较实况分析都偏高4℃左右，经过误差订正后都降低了2～3℃，集成后北部山区和平原北部温度进一步降低，与观测非常接近。对于10 m风速，模式原始预报中平原地区的风速比观测明显偏强，经过订正和集成，这一地区风速偏强的程度逐步减弱，集成之后平原地区的风速误差由3～4 m·s-1降低到1～2 m·s-1。对于2 m相对湿度，在大部分预报区域较观测明显偏低，总体偏低20%～30%，误差订正后误差明显减小，但在预报中南部地区有过订正的问题，相对湿度比观测略微偏大，而集成后又重新减小，基本分布和数值都与观测非常相似，说明订正集成后的结果都明显地减小了整个区域的预报误差。

图5 2021年3月9日00时起报24 h预报的(a～d)2 m温度，(e～h)10 m风速，(i～l)2 m相对湿度的水平分布对比(a,e,i)观测,(b,f,j)CMA-MESO 1 km模式原始预报,(c,g,k)CMA-MESO 1 km订正结果,(d,h,j)多模式集成结果Fig.5 Comparison of horizontal distribution of (a-d) 2 m temperature, (e-h) 10 m wind speed, (i-l) 2 m relative humidity in the 24 h forecast started from 00：00 UTC 9 March 2021(a, e, i) observation, (b, f, j) CMA-MESO 1 km model original forecast, (c, g, k) CMA-MESO 1 km correction, (d, h, j) multi-model blending

3.4.2 BMA概率预报特征分析

BMA方法不但可以得到确定性预报值，它的优势还在于可以得到预报场的概率预报特征。以2021年3月9日00时起报24 h温度预报为例进行BMA概率预报分析。图6为逐小时区域格点平均的2 m温度BMA百分位预报和观测对比。BMA方法通过分析百分位预报数据，可对其不确定性给出定量的估计。由图可见，逐小时的观测基本落在40～60百分位上，说明BMA预报的40～60百分位的2 m温度能将实况比较好地包含进去，而BMA确定性预报能较好的预报当天各预报时效的温度状况。

图6 2021年3月9日00时起报逐小时区域格点平均的2 m温度BMA百分位预报和观测对比Fig.6 The area-averaging 2 m temperature comparison of BMA percentile forecasts and observations started from 00:00 UTC 9 March 2021

对研究时段内单个格点的各要素进行BMA概率预报研究。BMA概率预报可以给出全概率的PDF结果，表征对集合预报不确定性的概率估计。如果PDF曲线越尖，区间范围越窄，说明BMA预报的不确定性更小。图7分别给出地形高度较低的平原格点(38°N、117°E)和北部地形高度较高的山地格点(41.5°N、117°E)2 m温度和10 m风速的PDF曲线。其中图7a和7b分别为平原格点和山地格点的2 m温度预报PDF，图7c和7d为两个格点的10 m风速预报PDF。图7中黑色曲线为BMA预报的PDF，黑色垂直实线为BMA确定性预报，蓝色垂直实线为同一格点的观测，两条红色垂直虚线分别为BMA预报PDF的10、90百分位预报值。从2 m温度预报的PDF曲线可见，平原格点2 m 温度的PDF曲线峰值为0.34，BMA的确定性预报位于曲线峰值的位置，与观测之间的误差为0.73℃，而PDF的10～90百分位温度范围在5.6～9.3℃，表明温度预报最大可能落在此范围内。山地格点的2 m温度PDF曲线峰值为0.23，确定性预报与格点观测误差为0.74℃，10～90百分位间的温度范围为-7.5～0.86℃，与平原格点比较，平原格点的曲线明显更尖更窄，说明山地格点温度预报的不确定性较平原站点要大，与实际的预测相符。综合上述分析，BMA方法能给出合理的不确定性的预测。

图7 2021年3月9日00时起报(a,b)2 m温度和(c,d)10 m风速的24 h预报PDF(a,c)平原格点(38°N、117°E),(b,d)山地格点(41.5°N、117°E)(黑色曲线：BMA预报PDF，黑色垂直实线：BMA确定性预报，蓝色垂直实线：观测，红色垂直虚线BMA预报PDF的10和90百分位预报)Fig.7 BMA predictive PDF of (a, b) 2 m temperature and (c, d) 10 m wind speed in 24 h forecast started from 00:00 UTC 9 March 2021 at (a, c) Plain grid (38°N, 117°E) and (b, d) Hilly Area grid (41.5°N, 117°E) (black solid curve: BMA predictive PDF， black solid vertical line: BMA deterministic forecast， blue solid vertical line: observation， red dashed vertical lines: the 10th percentile and 90th percentile forecasts for BMA predictive PDF)

从10 m风速预报的PDF看，两个格点的PDF曲线也有明显差异。山区格点较平原格点相比， PDF曲线峰值较高，曲线又尖又窄，表明此平原站点预报的不确定性更大。这个特点与CMA模式在平原的风速预报偏大明显，预报误差较大有关，在应用此预报结果时需要采用一定的概率值。

从单个格点的概率预报可了解温度和风速在某一格点上预报值的不确定性，但是单个格点不能完全反映区域整体特点。接着从区域的角度分析CMA模式BMA概率预报的特点。图8给出了CMA多模式集成的2 m温度以BMA 确定性结果为中心，区间为2℃的概率分布(图 8a)，以及10 m风速以BMA确定性结果为中心，区间为2 m·s-1的概率分布(图8b)。由此判断不同地区选取哪一个概率下的预报结果更合理。从2 m温度预报的概率分布可见，概率分布主要受地形高度和海陆分布的影响，在右侧渤海湾地区的概率值最大，陆地较海洋的概率值是减小的。陆地上在北京城区及以南的河北省的平原地区，概率值较大，为50%～80%，而在区域西北部山区概率值是减小的，概率在20%～50%。说明山区的温度预报方差和预报不确定性是较大的。这与BMA的2 m温度预报的误差分布很相似，预报不确定性较大的地区其BMA确定性预报的误差较大。

图8 CMA模式(a)2 m温度以BMA确定性结果为中心，区间为2℃的概率分布；(b)10 m风速以BMA确定性结果为中心，区间为2 m·s-1的概率分布Fig.8 The probability distribution of (a) 2 m temperature centered as BMA deterministic hindcast with the interval length of 2℃, and (b) 10 m wind speed centered as BMA deterministic hindcast with the interval length of 2 m·s-1

对于10 m风速的概率分布，概率值较大的地区位于试验区域的西北部山区以及与平原地区的交界处，概率可达70%～90%，说明预报值的不确定性很小，风速的预报是较为准确的。而在其他地区概率有所减小，在30%～50%。这一分布与原始CMA模式风场预报误差相似。概率分布的情况可以很好地说明预报的不确定性，因此可根据区域差异合理选取某一概率下的预报结果。

4 结论与讨论

基于CMA模式体系的CMA-GFS、CMA-REPS、CMA-MESO 3 km、CMA-MESO 1 km四个模式的2 m温度、10 m风速、2 m相对湿度等近地面要素预报，对京津冀地区进行误差订正和贝叶斯模式平均(BMA)方法多模式集成。对比了每个模式原始误差、订正后的误差以及多模式集成误差；比较了不同训练期结果确定最优训练期；分析了模式集成过程中各模式的权重特点，以及误差在预报区域内的水平分布特点等，得到以下主要结论：

(1)通过最优训练期长度选取试验，发现在20～40 d，不同训练期对BMA方法的要素预报的误差先减小后增大，训练期长度在30 d可得到综合最优的预报效果。

(2)通过对比每个模式原始误差、订正后的误差以及多模式集成误差，结果显示每个模式订正后的均方根误差都较原始模式预报有明显的减小，而之后多模式集成的预报效果比其中任一模式订正后的误差更优。2 m温度集成预报误差较原始模式的改善在0.5～1.4℃，改善率为20%～40%；10 m风速和2 m相对湿度的均方根误差改善率分别为12%～45%和25%～35%。

(3)通过BMA方法四个模式各时效的集成权重系数对比，显示各要素各时效的集成权重根据各模式的预报效果动态改变，当某一模式预报误差相对较小时，集成权重系数相对较大，反之亦然。如CMA-GFS模式的风速误差明显小于其他三个模式，其权重系数达到0.4～0.55。

(4)通过对比CMA-MESO 1 km原始模式及订正、集成后的各要素预报，从均方根误差的多日平均水平分布和个例分析，不同要素在不同地形高度处误差分布明显不同，温度误差较大的地方分布在北京城区西北地形较高的山区，10 m风速和2 m相对湿度的误差分布与温度分布正相反，相对较大的地区分布在城区及以南地区。经过订正集成后整个地区的误差都有明显减小，要素水平分布通过订正和集成逐渐向观测靠近，温度误差减小1～2℃，风速误差减小0.5～4 m·s-1，相对湿度降低10%～20%。

(5)BMA方法通过分析其百分位预报数据，对不确定性给出定量的预计。BMA预报的概率分布情况能较好地说明预报的不确定性，并将实际大气可能发生状态缩小到一个更小的区间范围，预报的不确定性减小。

通过将每个模式分别进行误差订正后再进行多模式集成的方法，既能够明显减小单个模式的预报误差，又能对各个模型结果进行综合集成，发挥各模型优势，使模式集成预报效果优于任一单个模式。因此这一方法切实有效，既汇集了CMA模式体系总体优势，获得可靠的确定性预报结果，也提供完整的概率密度函数(PDF)，对极端天气事件的概率预报技巧进行研究和评估。