一种新型可伸缩轮刺月球车的越障特性分析

张明顺

(沈阳理工大学 机械工程学院，辽宁 沈阳110159)

月球的地表环境非常复杂，月球车对车轮的性能要求很高。带轮刺的传统车轮在平整地形上运动时会产生多边形效应而影响月球车的运动稳定性；在经过障碍物时会以一定的速度与障碍物发生碰撞，使车轮产生震动冲击而影响月球车行驶的平顺性[1]。为解决传统月球车的这些问题，需要开发一种可伸缩轮刺的新型月球车。这种新型月球车在平整地形上运动时，通过轮刺收缩可减少多边形效应对月球车运动稳定性的影响；在遇到障碍物时伸出轮刺，使月球车能够较平稳地越过不同高度的障碍物，从而提高月球车的科学考察工作效率[2]。本文将主要分析这种新型可伸缩轮刺月球车的越障特性。

1 平整地形上的多边形效应

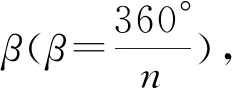
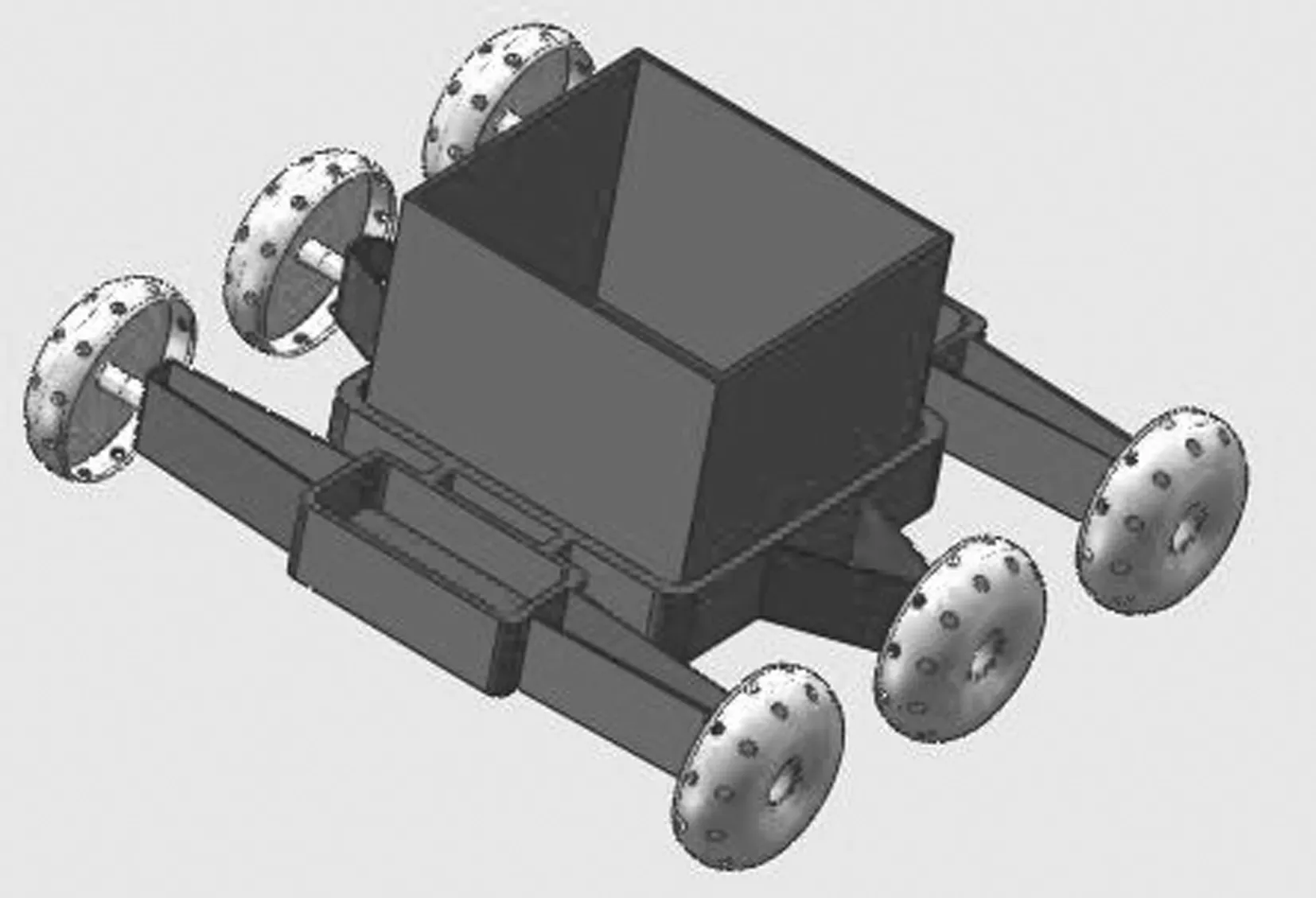
图1 传统月球车

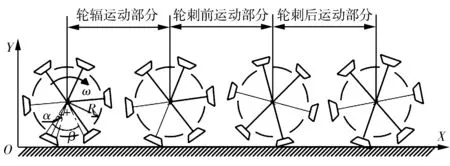
图2 带轮刺车轮在平整地形上运动的示意图

根据文献[1],在轮辐运动部分，即车轮轮辐与地面接触时，车轮质心高度(即质心与地面的距离)不变，车轮质心的位移为：

(1)

从上一个轮刺末端与地面的接触开始，到下一个轮刺前半部分与地面的接触终止，这个运动过程为轮刺前运动部分。对应这一运动过程，车轮质心随车轮运动逐渐降低，车轮质心的位移为：

(2)

从上一个轮刺前半部分与地面的接触开始，到下一个轮刺始端与地面的接触终止，这个运动过程为轮刺后运动部分。对应这一运动过程，车轮质心随车轮运动逐渐升高，车轮质心的位移为：

(3)

对式(1)-式(3)进行归纳，可得出车轮质心的位移规律。带固定轮刺车轮在平整地形上运动过程中，车轮质心的位移可表示为：

(4)

对车轮质心位移进行求导，可得出车轮质心在轮辐运动部分的运动速度，即

(5)

车轮质心在轮刺前运动部分的运动速度为：

(6)

车轮质心在轮刺后运动部分的运动速度为：

(7)

对式(5)-式(7)进行归纳，所得带固定轮刺车轮在平整地形上运动过程中，车轮质心的运动速度为：

(8)

对车轮质心的运动速度进行求导，可得出车轮质心在轮辐运动部分的运动加速度，即

(9)

车轮质心在轮刺前运动部分的运动加速度为:

(10)

车轮质心在轮刺后运动部分的运动加速度为:

(11)

对式(9)-式(11)进行归纳，所得带固定轮刺车轮在平整地形上运动过程中，车轮质心的运动加速度为：

(12)

分析可知：带固定轮刺的月球车行走在平整地形上时，车轮质心的运动规律不仅与车轮转动的角速度ω有关，还与轮刺所对的圆心角α和两根轮刺的夹角β有关；α越大，即车轮表面的轮刺与地面接触面积越大，则车轮质心在Y方向运动的位移、速度、加速度越大，车轮所受振动冲击也就越大；车轮周向轮刺的数量越多，即在轮刺所对的圆心角α不变时两根轮刺的夹角β越小，则车轮质心在Y方向运动的位移、速度、加速度越小。

2 可伸缩轮刺的车轮结构

若月球车采用可伸缩轮刺的车轮(图3)，且其在平整地形上运动时能将轮刺缩回，则可很好地弥补传统月球车的不足。

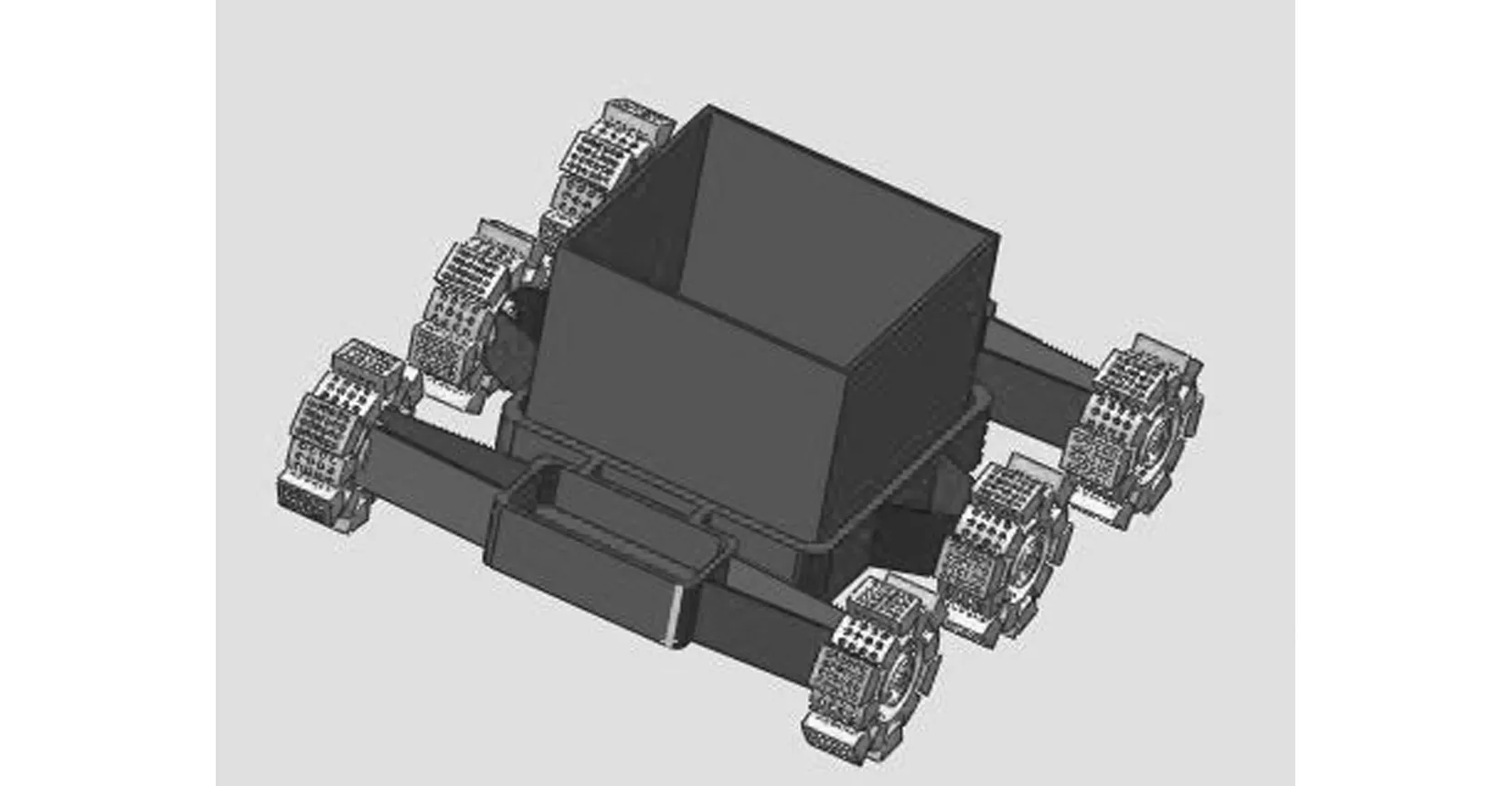
图3 有可伸缩轮刺车轮的月球车示意图

可伸缩轮刺车轮的主体主要由车轮轮辐和多个可伸缩的轮刺组成，每个轮刺都有一个一体式驱动单元[4]。驱动单元是实现轮刺伸缩的关键，它主要由压力传感器、位移传感器和伸缩结构组成。伸缩结构主要由电机、丝杠、螺母和伸缩杆组成。车轮轮刺的伸缩结构如图4所示。

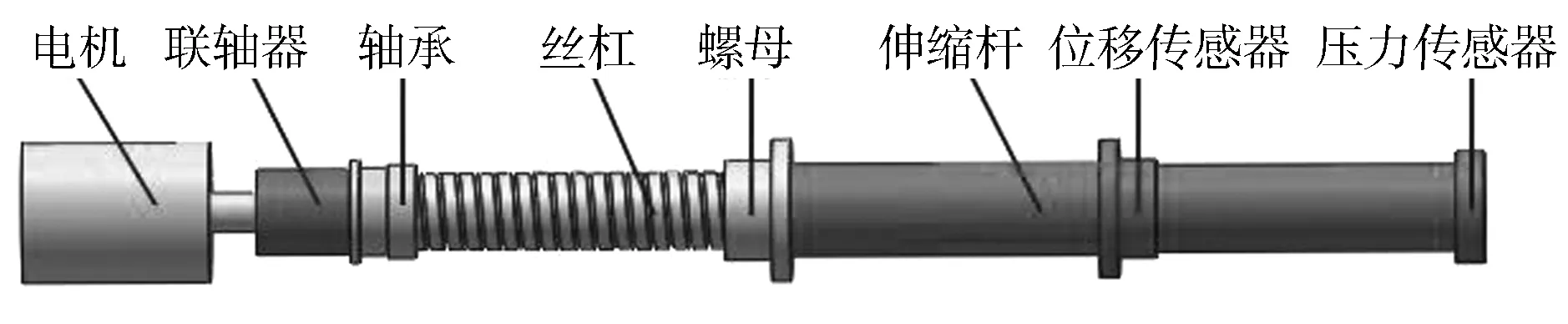
图4 车轮轮刺的伸缩结构

有可伸缩轮刺车轮的月球车感知到地形变化时，会将信号传递到控制器；控制器控制电机转动，进而带动丝杠转动；丝杠再带动螺母做直线运动，而螺母和伸缩杆是固定在一起的，故可实现伸缩杆的伸缩。待伸缩杆伸缩完毕，压力传感器和位移传感器会将信号再次反馈到控制器。车轮的轮刺可以在较短时间内完成伸缩任务，且整个伸缩过程是闭环控制的。可伸缩轮刺车轮的结构如图5所示。

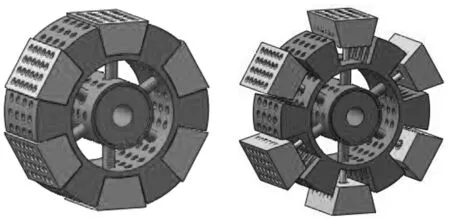
(a) 轮刺回位状态 (b) 轮刺伸出状态

3 可伸缩轮刺车轮越障时的受力分析

由文献[5]可知，新型可伸缩轮刺月球车的结构参数如表1所示。

表1 新型可伸缩轮刺月球车的结构参数

在月球车经过障碍物时，车轮与障碍物的接触面上存在阻力作用。设障碍物是固定在地面上的，则月球车在前轮接触障碍物瞬间的受力情况如图6所示。

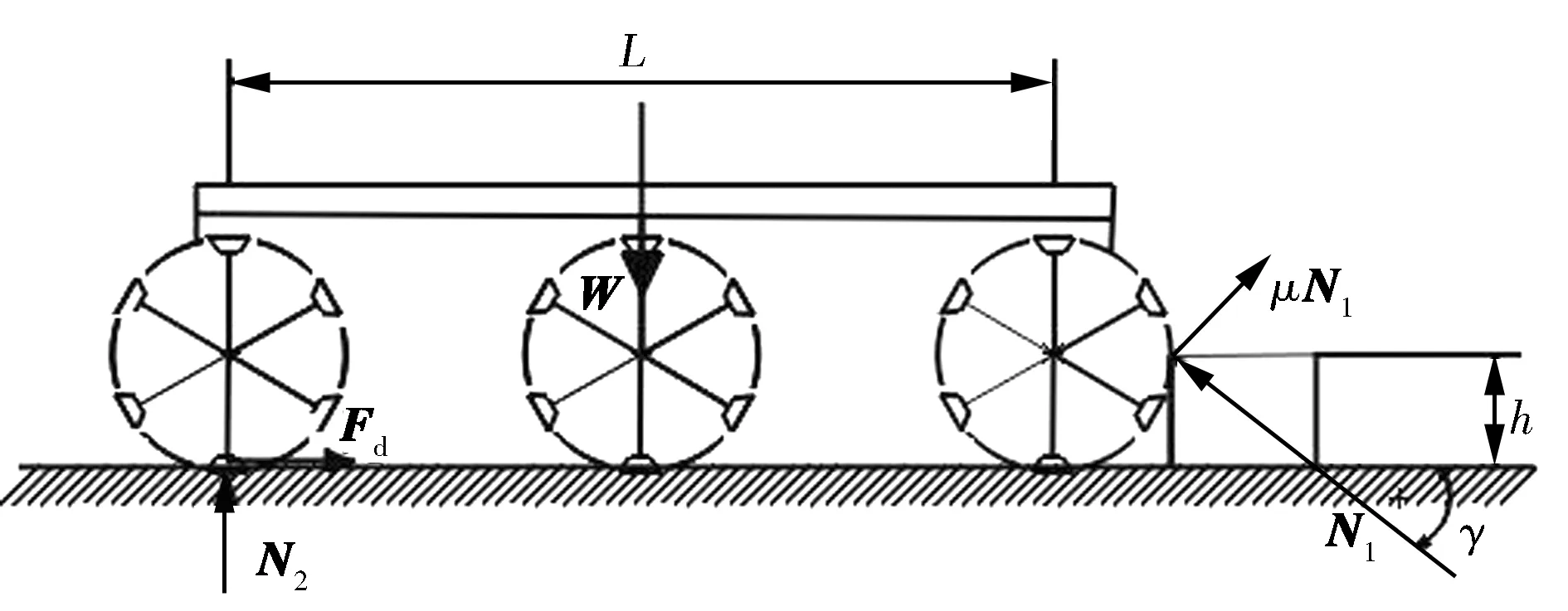
N1、N2分别为前、后轮所受地面支撑反力；L为前后轴的轴距，h为障碍物高度，Fd为车轮牵引力；W为作用在月球车上的总重力；μ为车轮的附着系数；γ为车轮接触障碍物的特殊角度

前轮越障的阻力为：

F=N1cosγ-μN1sinγ

(13)

角度γ为障碍物高度h和车轮半径R的函数,即

γ=arcsin[(R-h)/R]

(14)

前轮离地瞬间的力平衡方程为：

(15)

前轮离地瞬间的力矩平衡方程为：

μN1R+FdR—N2L+WL/2=0

(16)

由式(13)-式(16)可求得前轮越障的阻力F,即

(17)

设定L=1 800 mm,h=100 mm，μ=0.4，则由式(17)可绘制前轮越障阻力与车轮直径的关系曲线(图7)。

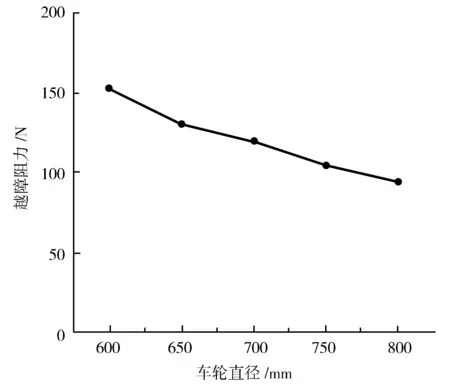
图7 前轮越障阻力与车轮直径的关系曲线

由图7可看出，车轮直径越大，越障时阻力就越小。同理，可对后轮越障的阻力进行分析。这里不予赘述。

当有可伸缩轮刺车轮的月球车遇到障碍物时，轮刺伸出，增大了车轮直径，进而减小了越障的阻力，使月球车能够更好地越过障碍物。

4 可伸缩轮刺车轮的越障过程仿真

4.1 月球地表环境的模拟

月球表面大多区域覆盖着岩石碎片、沙粒和灰尘，月壤松软，石块散落，地形复杂多变。其中，岩石碎块有大有小，但直径一般不超过500 mm[6]。此外，月球上地形起伏，障碍物坡度在25°左右，月球表面还有特殊的陨石撞击坑，存在一些较深且宽的坑状极端地形。这都会对正常行驶的月球车造成一定影响。

为了真实地模拟月球的地表环境，本文根据文献[7-9],在构建图8所示的月球表面障碍物分布模型时，将模型中台阶障碍物的高度设定为150 mm、300 mm和500 mm这3种，而将斜坡障碍物的坡度设定为30°。

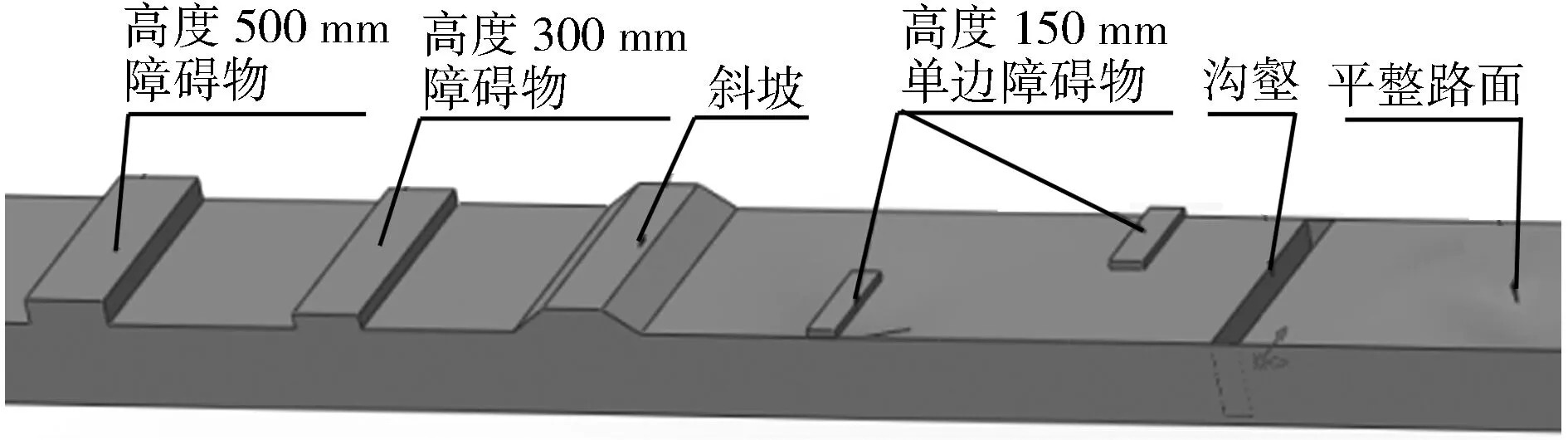
图8 月球表面的障碍物分布模型

4.2 月球车越障过程仿真条件的设置

本文将传统月球车与新型可伸缩轮刺月球车的模型参数先后导入ADAMS仿真软件，分别进行了两种月球车越障过程的仿真。

鉴于月球表面覆盖着松软的月壤，其地面参数与土路比较接近，本文在查阅文献[10-12]后，设置了下列仿真条件：月球车材料为铝合金，总质量为400 kg；月球表面的重力加速度为1.634 m/s2；月球车驱动角速度为30 °/s；地面刚度系数为10，静摩擦系数为0.8，动摩擦系数为0.5。

4.3 两种车轮质心高度变化的对比分析

通过仿真，可得图9所示两种月球车左前轮质心高度的变化曲线。月球车右前轮质心高度的变化曲线与左前轮类似，这里不再罗列。

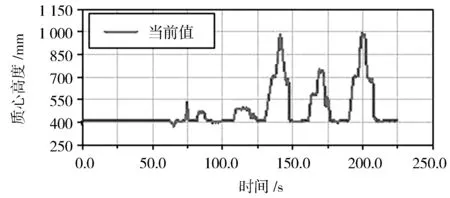
(a) 可伸缩轮刺车轮

分析可知：新型可伸缩轮刺月球车可以轻松地越过3处高度分别为150 mm、300 mm和500 mm的障碍物，且能够在平整月面甚至是斜坡的月面上较平稳地行驶；而传统月球车虽然也可在平整月面上平稳行驶，但是相比于新型可伸缩轮刺的月球车来说，在越过高度不同的障碍物时，其前轮质心的高度变化较大，高度变化的最大值约为620 mm(而可伸缩轮刺车轮质心高度变化的最大值约为590 mm),会产生较大波动，对月球车行驶的平顺性产生不利的影响。当通过沟壑地形时，传统月球车比新型可伸缩轮刺月球车的车轮质心高度变化要大。

仿真还发现，传统月球车在经过高度为500 mm的障碍物时会出现打滑现象，而无法越过障碍物。

4.4 两种车轮质心运动加速度的对比分析

通过仿真，可得图10所示两种月球车前轮质心在Y方向的运动加速度曲线。

月球车前轮质心在Y方向运动加速度的值反映了地面对前轮造成冲击的强弱，是衡量月球车行驶平顺性的重要指标[13]。分析可知，前轮质心在Y方向运动加速度值的波动一般出现在前轮经过障碍物或者越过沟壑时，障碍物越高，前轮质心在Y方向运动加速度值的波动就越大。

由图10可看出：新型可伸缩轮刺月球车在其前轮经过障碍物或者沟壑时，前轮质心在Y方向运动的加速度值一般在1 000 mm/s2上下变化，其最大值约为2 000 mm/s2；传统月球车在其前轮经过障碍物或者沟壑时，前轮质心在Y方向运动加速度的值波动较大，最大时超过了5 000 mm/s2，是可伸缩轮刺车轮的2倍多，此时对月球车行驶的平顺性会产生巨大的负面影响。

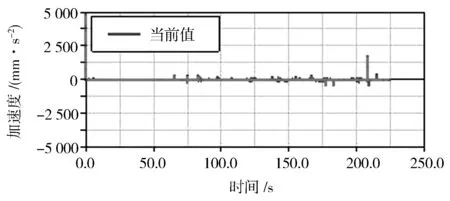
(a) 可伸缩轮刺左前轮

4.5 两种车轮驱动扭矩的对比分析

通过仿真，可得图11所示两种月球车前轮的驱动扭矩曲线。

由图11(a)、(b)可看出：可伸缩轮刺月球车前轮在启动时驱动扭矩较大，启动后行驶中所需驱动扭矩则比较小，因为此时只需克服车轮的滚动阻力即可；在月球车经过障碍物时，前轮的驱动扭矩较大，其最大值接近3.5×105N·mm；月球车左前轮与右前轮接触障碍物的点不同，所需驱动扭矩也不同。由图11(c)、(d)可看出：传统月球车在平整月面上运动时，其前轮的驱动扭矩比可伸缩轮刺前轮的小，这是传统月球车的优势所在；但是在越障时，传统月球车需要的前轮驱动扭矩比较大，最大值超过了1.2×106N·mm，远大于可伸缩轮刺月球车前轮的驱动扭矩。

(a) 可伸缩轮刺左前轮

4.6 两种车轮与月球表面接触力的对比分析

通过仿真，可得图12所示两种月球车前轮与月球表面的接触力曲线。

(a) 可伸缩轮刺左前轮

由图12(a)、(b)可看出：可伸缩轮刺月球车在平整的月球表面行驶时，由于可伸缩轮刺的作用，其前轮与月球表面的接触力曲线呈周期性变化，比较均匀；当月球车经过障碍物或者沟壑时，其前轮会受到障碍物或者沟壑撞击，导致前轮与月球表面的接触力增大，其最大值为1 500 N。由图12(c)、(d)可看出：传统月球车在平整的月球表面行驶时，其前轮与月球表面的接触力较小；当月球车经过障碍物或者沟壑时，其前轮会受到障碍物或者沟壑撞击，导致前轮与月球表面的接触力急剧增大，其最大值可达5 500 N，这不仅影响月球车行走的平顺性，还会加剧车轮的磨损[14]，缩短车轮的使用寿命。

5 结 语

(1) 通过推导月球车在平整地面上行驶的质心运动方程，说明了带固定轮刺车轮在运动过程中轮刺对车轮质心位移、运动速度和运动加速度的影响；进一步说明，可伸缩轮刺车轮在平整地面上行走时，通过轮刺收缩，可很好地弥补传统月球车的不足。

(2) 通过建立月球车在越障过程的力学分析方程，分析了车轮直径与越障阻力的关系。结果表明，车轮直径越大，越障阻力就越小。可伸缩轮刺车轮通过伸出轮刺能直接增大车轮的直径，减小越障阻力，提高月球车的越障能力。

(3) 在ADAMS软件中建立仿真模型后进行了动力学分析，并以可伸缩轮刺月球车车轮与传统月球车车轮的仿真结果对比证明，可伸缩轮刺车轮的月球车可以更轻松地越过障碍物。